что такое однородные величины

Понятие измерения величины. Свойства скалярных величин.

Понятие измерения величины. Свойства скалярных величин.

Величина – неопределяемое понятие.

(Мы понимаем так: величина – это размер. Аристотель писал: «То или иное количество есть множество, если его можно счесть; есть величина, если его можно измерить».)

Под величиной понимают особые свойства реальных объектов или явлений.

-Какие величины вы знаете? (дл, масса, емкость…)

-Какие тройки взаимосвязанных величин? (ск, вр, рас)

-Каким методом пользуется учитель в нач. школе при ознакомлении с величинами (длиной)? (практическим)

Длина – это свойство предметов иметь протяжённость.

Масса – с математической точки зрения это такая положительная величина, которая обладает свойствами:

масса одинакова у тел, уравновешивающих друг друга на весах;

масса складывается, если тела соединяются вместе.

-Какие бывают величины?

(Разнородные величины- величины, которые выражают разные свойства объектов.

-Какие ещё бывают величины? (в геометрии векторная, скалярная; положительная, отрицательная; переменная, постоянная).

-Какие величины называются скалярными?

(Скалярные величины – величины, не имеющие направления или которые определяются одним численным значением.)

-Назовите свойства скалярных величин.

Свойства однородных скалярных величин

Любые две однородные величины сравнимы : они либо равны, либо одна меньше другой.

Т.е. для любых величин a и b справедливо одно и только одно из отношений:

Например, длина гипотенузы больше длины катета; масса яблока меньше массы арбуза, длины противоположных сторон прямоугольника равны.

Т.е. для любых величин a и b однозначно определяется величина

Например: пусть а- длина отрезка АВ, в – длина отрезка ВС. Тогда длина отрезка АС равна сумме длин отрезков АВ и ВС.

3. Величину можно умножать на неотрицательное действительное число, получая в результате число того же рода.

Например: если длину а отрезка АВ умножить на х=2, то получим длину 2а нового отрезка АС.

Например: Пусть а – длина отрезка АС, в – длина отрезка АВ, тогда длина ВС есть разность длин АС и АВ.

5. Величины одного рода делят, определяя частное через произведение величины на число:

Частным величин а и в называется такое неотрицательное действительное число х, что

Понятие измерения величины. Свойства скалярных величин.

Определение: Измерить величину значит сравнить её с некоторой величиной того же рода, принятой за единицу.

Определение: Если дана величина а и выбрана единица величины е, то в результате измерения величины а находят такое действительное число х, что а = x ● е.

Число x называют численным значением величины а при единице величины е.

Например, 8 кг = 8 1 кг.

Используя это, а также определение умножения величины на число, можно обосновать процесс перехода от одной единицы величины к другой.

Выразить 1/5 часа в минутах.

1/5 ч = 1/5 ● 1 ч = 1/5 ● 60 мин = 60/5 мин = 12 мин.

Измерение величин позволяет свести сравнение их к сравнению чисел; операции над величинами к операциям над числами.

Не следует смешивать длину (она одна для отрезка) с численным значением длины, оно различно в зависимости от единицы измерения.

АВ = 4 см = 40 мм = 0,4 м

Свойства скалярных величин

Если величины а и в измерены при помощи единицы величины е, то отношения между величинами а и в будут такими же, как и отношения между их численными значениями и наоборот:

Пример: Сравните: 8 кг и 6 кг

Если величины а и в измерены при помощи единицы величины е, то чтобы найти численное значение суммы а + в , достаточно сложить численные значения величин а и в :

а +в = 3 m + 7 m = (3 + 7) m = 10 m

Например, а = 5 км, b в 3 раза больше длины а, то есть

b = 3 ● а = 3 ● (5 км) = (3● 5) км = 15 км

В начальном курсе математики, в частности в системе Л.В. Занкова, операции над величинами выполняются параллельно с операциями над их численными значениями. Например, в теме «Сложение отрезков» результат сложения можно найти 2 способами.

а =5см, в = 4 см. найти а+в.

Первый способ заключается в том, что строится отрезок = 5см и подстраивается 4 см. Получится всего 9 см.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Скоростное чтение

Курс повышения квалификации

Специфика преподавания предмета «Родной (русский) язык» с учетом реализации ФГОС НОО

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1047428

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Только каждый 10-й россиянин может дать платное образование своим детям

Время чтения: 2 минуты

Отказавшихся от вакцинации сотрудников МГУ отстранили от работы со студентами

Время чтения: 1 минута

В России отцы охотнее дают деньги детям на карманные расходы, чем матери

Время чтения: 2 минуты

В России утвердили квоты приема на целевое обучение в вузах на 2022 год

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Понятие величины

Величина – одно из основных математических понятий, воз­никшее в древности и в процессе длительного развития подверг­шееся ряду обобщений. Длина, площадь, объем, масса, скорость и многие другие – все это величины.

Величина — это особое свойство реальных объектов или явле­ний. Например, свойство предметов «иметь протяженность» назы­вается «длиной». Величину рассматривают как обобщение свойств некоторых объектов и как индивидуальную характеристику свой­ства конкретного объекта. Величины можно оценивать количест­венно на основе сравнения.

Например, понятие длины возникает:

1) при обозначении свойств класса объектов («многие окружающие нас предметы имеют длину»);

2) при обозначении свойства конкретного объекта из этого
класса («этот стол имеет длину»);

3) при сравнении объектов по этому свойству («длина стола
больше длины парты»).

Однородные величины – величины, которые выражают одно и то же свойство объектов некоторого класса.

Разнородные величины выражают различные свойства объ­ектов (один предмет может иметь массу, объем и др.).

Свойства однородных величин:

1. Однородные величины можно сравнивать.

Для любых величин а и b справедливо только одно из отно­шений: а b, а = b.

Например, масса книги больше массы карандаша, а длина ка­рандаша меньше длины комнаты.

2. Однородные величины можно складывать и вычитать. В
результате сложения и вычитания получается величина того же рода.

Величины, которые можно складывать, называются аддитив­ными. Например, можно складывать длины предметов. В резуль­тате получается длина. Существуют величины, которые не явля­ются аддитивными, например, температура. При соединении воды разной температуры из двух сосудов, получается смесь, темпера­туру которой нельзя определить сложением величин.

Мы будем рассматривать только аддитивные величины.

3. Величину можно умножать на действительное число. В
результате получается величина того же рода.

Пример: «Налей в банку 6 стаканов воды».

Если объем воды в стакане – V,то объем воды в банке – 6V.

4.Однородные величины делят. В результате получается не­отрицательное действительное число, его называют отношением величин.

Источник

Основные положения однородных величин

Натуральное число как мера величины

Нам известно, что числа возникли из потребности счета и измерения. Если для счета предметов нам достаточно натуральных чисел, то для измерения нам необходимы действительные числа. В начальной школе в качестве результата измерения выступают натуральные числа. Мы также встанем на эту позицию, определив натуральное число как меру величины. Выясним, какой смысл имеют арифметические действия над натуральными числами с этой позиции.

Натуральные числа будем рассматривать в связи с измерением положительных скалярных величин: длин, площадей, масс, времени и др.

§1. Понятие положительной скалярной величины.

Рассмотрим два высказывания:

1.Многие окружающие нас объекты имеют длину;

2. Стол имеет длину.

Таким образом, термин «длина» применим для обозначения свойства целого класса объектов или одного объекта. Длина, это такое свойство объекта или объектов, которое проявляется в разной степени, т.е. можно сказать, что один стол длиннее другого, чего нельзя сказать о форме стола или о материале, из которого он сделан. Мы не можем сказать, что один стол «прямоугольнее» другого или «деревяннее»другого.

Таким образом, свойство «длина»- это особое свойство объектов, которое проявляется при сравнении их по протяженности. В процессе сравнения устанавливается, что два объекта либо имеют равные длины, либо длина одного больше длины другого объекта. Такие свойства объектов будем называть величинами.

Величины, выражающие одни и те же свойства объектов будем называть величинами одного рода или однородными величинами.

Основные положения однородных величин

1. Любые величины одного рода сравнимы: А=В либо А В.

2. Отношение «меньше» для однородных величин транзитивно: А А В.

5. Величину можно умножать на положительное действительное число, в результате получают величину того же рода х·А=В.

6. Величины одного рода можно делить, в результате получают число. Определение: Частным величин А и В называется такое положительное число х=А:В, что А=х∙В (деление определено через умножение величины на число).

Величины обладают одной особенностью, их можно оценить количественно. С этой целью величину надо измерить. Для измерения величины данного рода выбирают величину, называемую единицей измерения. Её будем обозначать Е.Если задана величина А и выбрана единица величины Е (того же рода), то измерить величину А – это значит найти такое положительное число х, что А=х·Е, х- численное значение величины А при выбранное единице величины Е или мера величины А при единице Е. Пишут х=m_Е(А).

Пример 1. А-длина отрезка а, Е- длина отрезка b, который в отрезке a укладывается 4 раза, тогда 4- мера длины отрезка а.

Пример 2. 2,6 кг=2,6∙кг, 13см=13·см, 16 с =16∙с.

Используя это представление, можно обосновать переход от одной единицы величины к другой.

ч= ·ч= ∙(60мин)= ( ∙60)мин=25мин.

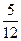
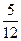
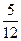
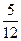
Определение.Величина, определяемая только численным значением, называется скалярной.

Определение.Величина, которая при выбранной единице измеренияопределяется положительным числом, называется положительной скалярной величиной.

Измерение величин позволяет переходить от сравнения величин к сравнению чисел, от действий над величинами к действиям над числами и наоборот.

1. Если величины А и В измерены с помощью единицы величины Е, то

2. Если величины А и В измерены с помощью единицы величины Е, то

Пример. А=5кг, В=3кг. =>А+В=5кг+3кг=(5+3)кг=8кг.

3. Если величины А и В таковы, что В=х∙А, а величина измерена с помощью единицы величины Е, то В=х∙А m(B)=х∙ m(A)

Пример. Еслимасса В в 3 раза больше массы А и А=2кг, то В=3 ∙А=3∙(2кг) =(3∙2)кг=6кг.

Рассмотренные понятия: объект (предмет, явление, процесс), его величина, её мера, единица величины- надо уметь вычленять в текстах и задачах.

Один и тот же объект может обладать несколькими величинами: для человека – рост (длина), масса, возраст (время), процесс равномерного движения связывает три величины S=V·t.

Аксиоматическое определение величины см. стр. 275.

Источник

Величины

Величины – это особые свойства реальных объектов или явлений. Например, свойство предметов иметь протяженность называется длиной. Это же слово мы употребляем, когда говорим о протяженности конкретных объектов.

Величины бывают однородные и разнородные. Однородные величины выражают одно и тоже свойство объектов некоторого множества. Например, длина дома и длина пути. Разнородные выражают различные свойства предметов. Например, длина комнаты и площадь комнаты.

Величины обладают следующими свойствами:

1. В пределах системы всех однородных величин устанавливается отношение неравенства: две величины а и b одного и того же рода или совпадают (a = b), или первая меньше второй (a a). Например, длина гипотенузы больше длины катета, масса одного апельсина меньше массы одного арбуза, площадь детской комнаты равна площади спальни и т.д.

2. Величины одного и того же рода можно складывать. В результате получается величина того же рода: a + b = c, где с называют суммой величин. Например, SS=S S S

3. Величину можно умножать на действительное число, получая величину того же рода: b = x a, где величина b называется произведением. Например, длину отрезка АВ = а умножим на 5. Получим новый отрезок АС = 5а.

5. Величины одного и того же рода делят: с = а : b, где с – частное, т.е. с такая величина, что а = b c. Например, отношение длины отрезка АВ = а к длине отрезка АС = с равно 2.

6. Некоторые величины разного рода умножают и делят, получая в результате величину третьего рода. Например, S = v t, S= a h.

Источник

Свойства однородных величин

1. Однородные величины можно сравнивать. Для любых величин А и В справедливо только одно из отношений: А В, А=В.

Например, масса книги больше массы карандаша, а длина ка­рандаша меньше длины стола.

2. Однородные величины можно складывать и вычитать. В резуль­тате получается величина того же рода.

Величины, которые можно складывать, называются аддитивны­ми. Например, можно складывать длины предметов. В результате получается длина. Существуют величины, которые не являются ад­дитивными, например температура. При соединении воды разной температуры из двух сосудов получается смесь, температуру которой нельзя определить сложением величин.

Мы будем рассматривать только аддитивные величины.

Пусть: А — длина ткани,

В — длина куска, который отрезали, тогда;

3. Величину можно умножать и делить на положительное дей­ствительное число. В результате получается величина того же рода.

2) «Раздели ленту на 4 равные части». Если длина ленты — L, то длина каждой ее части — L.4.

4.Однородные величины можно делить. В результате получается положительное действительное число, его называют отношением ве­личин. А:В=х о А—В-х.

5. Величину можно оценить количественно, то есть измерить.

Дети уже в дошкольном возрасте учатся выделять разные пара­метры размера предмета (длину, ширину, высоту), сравнивать пред­меты по этим параметрам (наложением и приложением), измерять протяженность условными мерками. Довольно рано происходит знакомство с площадью фигур, объемом жидких и сыпучих веществ, массой физических тел, промежутками времени. В быту дети накап­ливают необходимый опыт для последующего обучения, системати­зации и расширения знаний. Измерительная деятельность формиру­ется только под воздействием целенаправленного обучения. В на­чальной школе происходит знакомство с общепринятыми единицами величин (метром, литром, килограммом и др.).

Измерение величин

Сравнивая величины непосредственно, можно установить их равенство или неравенство.

Для получения более точного результата сравнения величины измеряют. Например, измеряя массу арбуза на чашечных весах, сравнивают ее с массой гири. Измеряя длину комнаты шагами, сравнивают ее с длиной шага.

Процесс сравнения зависит от рода величины: длину измеряют с помощью линейки, массу — используя весы. Каким бы ни был этот процесс, в результате измерения получается определенное чис­ло, зависящее от выбранной единицы величины.

Измерение заключается в сравнении данной величины с некото­рой величиной того же рода, принятой за единицу.

Цель измерения — получить численную характеристику данной величины при выбранной единице величины.

Измерить величину А — это значит найти такое положительное действительное число х, что А=х Е, где Е — величина того же рода, принятая за единицу. Число х называют численным значением вели­чины А при единице величины Е.

Численное значение величины показывает, во сколько раз за­данная величина больше или меньше величины, принятой за еди­ницу.

1) Если масса дыни 3 кг, то 3 — численное значение массы дыни при единице массы килограмм.

Величины, определяемые одним численным значением, называ­ются скалярными (длина, объем, масса и др.). Существуют еще век­торные величины, которые определяются численным значением и направлением (скорость, сила и др.). Мы будем рассматривать толь­ко скалярные величины (длину, площадь, объем, массу, время).

Значение измерения очень велико. Не всегда можно сравнить или сложить (вычесть) величины непосредственно (например, дли­ну дорог). Измерение позволяет свести сравнение величин к сравне­нию чисел, а действия с величинами — к действиям над числами, что значительно проще.

Источник