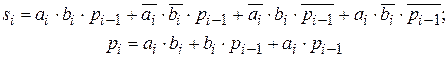что такое одноразрядный сумматор
Сумматор двоичных чисел
Логические схемы имеют практическое применение в вычислительной технике. Они используются:
Итак, как процессор выполняет математические операции?
Прежде всего, ответьте на вопросы:
— Каким образом должна быть представлена информация, чтобы с ней мог работать компьютер?
— Чтобы компьютер мог выполнять математические операции с числами, в какой системе счисления они должны быть представлены?
— Какие сигналы подаются на входы логических вентилей?
Вывод : таким образом и в двоичной системе счисления и в алгебре логики информация представлена в виде двоичных кодов.
И второй момент. Для того чтобы максимально упростить работу компьютера, все математические операции (вычитание, деление, умножение и т.д.) сводятся к сложению.
Вспомним таблицу сложения двоичных чисел. Запишем ее в несколько иной форме.
Обратите внимание на дополнительный столбец. Его мы ввели потому, что при сложении происходит перенос в старший разряд. Обозначим его Р и закончим заполнение таблицы.
Проанализируем полученный результат.
Построим к этому логическому выражению логическую схему:
Проследим за изменением сигнала при прохождении через схему:
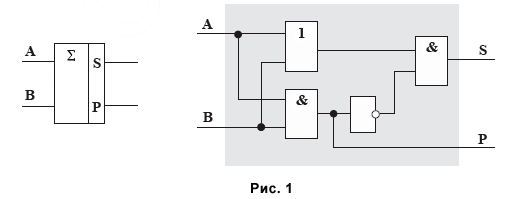
Полученная нами схема выполняет сложение двоичных одноразрядных чисел и называется полусумматором, так как не учитывает перенос из младшего разряда в старший (выход P ).
Сумматор – это логическая электронная схема, выполняющая сложение двоичных чисел. Сумматор является главной частью процессора.
Рассмотрим принцип работы одноразрядного двоичного сумматора.
Одноразрядный сумматор должен иметь три входа: А, В – слагаемые и Р 0 – перенос из предыдущего разряда и выходы: S – сумма и Р – перенос.
Нарисуем одноразрядный сумматор в виде единого функционального узла:
Связь между двоичной арифметикой и алгеброй логики позволяет реализовать логические схемы основных элементов процессора и памяти компьютера.
Рассмотрим сначала более простое устройство – полусумматор.
| A | B | P | S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
По данной таблице истинности построим СДНФ (см. алгоритм построения СДНФ):
Преобразуем логическую формулу для S:
(¬ A • B) + (A • ¬ B) = (¬ A • A) + ( ¬ A • B) + (A • ¬ B) + (¬ B • B) =
= ¬ A • (A + B) + ¬ B • (A + B) = (A + B) • ¬ (A • B)
С учетом формулы для переноса имеем:
S = (A + B) • ¬ (A • B) = (A + B) • ¬ P
Таким образом, полусумматор можно построить, используя четыре простейших логических элемента: два конъюнктора, дизъюнктор и инвертор (см. рис.1, слева показано условное обозначение полусумматора):
Итак, получено устройство, реализующее суммирование одноразрядных двоичных чисел без учета переноса из младшего разряда.
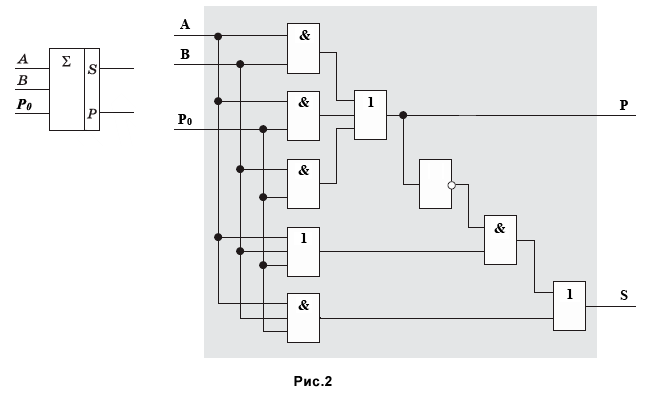
Для реализации полного одноразрядного сумматора необходимо учесть перенос из младшего разряда (P0). Поэтому сумматор должен иметь три входа. Построим таблицу истинности для устройства с учетом третьего входа:
| A | B | P0 | P | S |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Построим СДНФ для выхода P (перенос в старший разряд):
P =(¬ A ∧ B ∧ P0) ∨ (A ∧ ¬ B ∧ P0) ∨ (A ∧ B ∧ ¬ P0) ∨ (A ∧ B ∧ P0)
Преобразуем:
1) (A ∧ B ∧ ¬ P0) ∨ (A ∧ B ∧ P0) = (A ∧ B) ∧ (¬ P0 ∨ P0) = A ∧ B
Имеем, P = (¬ A ∧ B ∧ P0) ∨ (A ∧ ¬ B ∧ P0) ∨ (A ∧ B)
2) (¬ A ∧ B ∧ P0) ∨ (A ∧ B) = B ∧(¬ A ∧ P0 ∨ A) = B ∧ (¬ A ∨ A ) ∧ (P0 ∨ A) =
= B ∧ (P0 ∨ A) = (B ∧ P0) ∨ (A ∧ B)
Имеем, P = (A ∧ ¬ B ∧ P0) ∨ (B ∧ P0) ∨ (A ∧ B)
3) (A ∧ B) ∨ (A ∧ ¬ B ∧ P0) = A ∧ (B ∨ ¬ B ∧ P0) = A ∧ (B ∨ ¬ B)(B ∨ P0) =
= A ∧ (B ∨ P0) = (A ∧ B) ∨ (A ∧ P0)
Таким образом, для переноса в старший разряд получили:
P = A ∧ B ∨ A ∧ P0 ∨ B ∧ P0
Проанализируем таблицу истинности для выхода S. Значение S отлично от нуля в том случае, если единица поступает ровно на один вход (при этом на двух других входах фиксируется ноль), или на все три входа сразу, т. е.:
S = ¬ (A ∧ B ∨ A ∧ P0 ∨ B ∧ P0) ∧ (A ∨ B ∨ P0) ∨ (A ∧ B ∧ P0)
С учетом формулы для переноса в старший разряд, имеем:
S = ¬ P ∧ (A ∨ B ∨ P0) ∨ (A ∧ B ∧ P0)
Таким образом, одноразрядный двоичный сумматор можно реализовать с помощью следующей схемы (см. рис. 2, слева показано условное обозначение сумматора), которая соответствует полученным логическим формулам (1) и (2).
Заметим, что логические функции P и S можно выразить с помощью других формул. В таком случае для одноразрядного двоичного сумматора потребуется другая логическая схема.
Copyright © 2014-2021, Урок информатики
Все права защищены
Одноразрядный сумматор



Сумматоры выполняют арифметическое сложение чисел, которое производится начиная с младших разрядов чисел. В каждом разряде сумматора выполняются одинаковые действия, т. е. суммируются две двоичные цифры в соответствии с правилами сложения двоичных цифр.
При сложении двух единиц возникает единица переноса в старший разряд, которую нужно учесть при сложении цифр следующего разряда. Поэтому в каждом разряде сумматора необходимо предусмотреть возможность суммирования трех цифр: двух цифр слагаемых и единицы переноса из младшего разряда. В свою очередь, в каждом разряде необходимо сформировать не только значение одного разряда суммы, но и значение единицы переноса в соседний старший разряд. Таким образом, сумматор для сложения многоразрядных чисел можно построить из одинаковых схем, каждая из которых выполняет сложение двух цифр слагаемых и переноса из младшего разряда. Такая схема называется одноразрядным сумматором. Одноразрядный сумматор представляет собой комбинационную схему с тремя входами и двумя выходами, логика работы которой соответствует следующей таблице истинности (табл. 2.13).
Таблица 2.13. Логика одноразрядного сумматора
| Входы | Выходы | |||
| ai | bi | pi-1 | si | pi |
В соответствии с таблицей истинности уравнения выходов после минимизации имеют следующий вид:
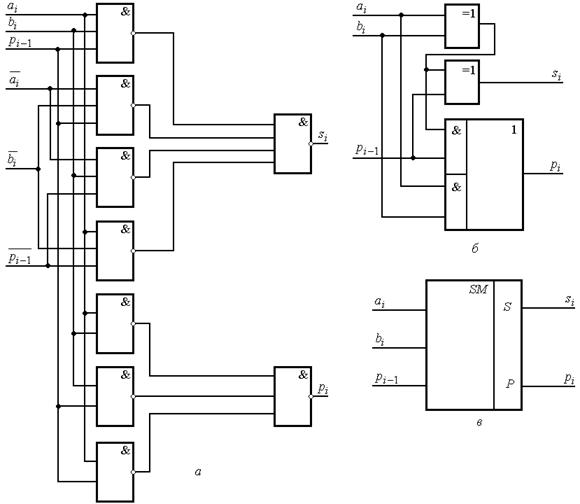
Схемы одноразрядного сумматора и его условное графическое обозначение показаны на рис. 2.25.
Рис. 2.25. Одноразрядные сумматоры:
а – схема сумматоров на элементах И-НЕ;
б – схема сумматора с использованием элементов сложения по модулю 2;
в – условное графическое обозначение
Одноразрядные сумматоры
Суммирование двух чисел происходит поразрядно, с определением цифры в данном разряде и сигнала переноса в соседний, более старший разряд.
При суммировании младших разрядов требуется одноразрядный сумматор с двумя входами, поскольку входного сигнала переноса в этом разряде нет. Такие сумматоры, в отличие от сумматоров с тремя входами, называют полусумматорами (рис. 2.7).
Рис. 2.7. Таблица истинности (а), схема (б) и условное графическое обозначение (в) полусумматора
Из таблицы истинности (рис. 2.7, а) следуют аналитические выражения функций суммы S и выходного сигнала переноса CRO (от carry output) в СДНФ:
По этим формулам синтезирована схема, показанная на рис. 2.7, б. В условном графическом обозначении (рис. 2.7, в) под сокращением HS подразумевается полусумматор.
Одноразрядный полный сумматор в отличие от полусумматора имеет три входа: для двух разрядов слагаемых (а и b) и входного сигнала переноса (СRI). В его условном обозначении (рис. 2.8) надпись SM является сокращением от слова summer.
Рис. 2.8 Условное графическое обозначение одноразрядного полного сумматора
Из анализа таблицы истинности (табл. 2.1) следует, что одноразрядный полный сумматор можно синтезировать на основе трех одноразрядных полусумматоров по схеме, представленной на рис. 2.9. Причем полусумматор, расположенный на этой схеме справа, можно заменить дизъюнктором.
Таблица истинности одноразрядного полного сумматора
Принцип работы сумматора
Сумматоры. Устройство, принцип работы
Сумматоры — это комбинационные устройства, предназначенные для сложения чисел.
Функционирование однозарядного сумматора показано в таблице, приведённой на рис.10.30. В этом случае при сложении слагаемых используется перевод десятичных чисел в двоичные числа.
Pиc.10.29. Символическое изображение одноразрядного двоичного сумматора
При сложении слагаемых или 0+1+0 получается десятичное число 1. Такому числу соответствует двоичное число 01, при этом Аналогично, 1+1+0 = 2, которому соответствует двоичное число 10, при этом . При сложении чисел 1+1+1 = 3, которому соответствует двоичное число 11, при этом и так далее.
Сумматоры могут быть последовательного и параллельного действия. В сумматорах последовательного действия коды двоичных чисел вводятся в последовательной форме слагаемое за слагаемым, начиная с младшего разряда.
На рис.10.31 изображена схема сумматора последовательного действия, предназначенного для суммирования четырёхразрядных двоичных чисел. Сумматор построен на трёх регистрах сдвига, D-триггере и на одноразрядном сумматоре.
Рис.10.30. Таблица функционирования одноразрядного сумматора
Рис.10.31. Схема сумматора последовательного действия
Функционирование сумматора приведено в таблице рис.10.32, где слагаемое pi для первого разряда всегда равно нулю.
Рис.10.32. Таблица функционирования сумматора
Для ускорения операции сложения используются сумматоры параллельного действия, которые состоят из нескольких однозарядных сумматоров. В таких сумматорах слагаемые поступают одновременно на соответствующие входы однозарядных сумматоров, при этом каждый из однозарядных сумматоров формирует на своих выходах суммы соответствующих разрядов и слагаемые переноса, передаваемых на входы старших разрядов. Схема четырёхразрядного сумматора параллельного действия приведена на рис.10.33.
Рис.10.33. Схема четырёхразрядного сумматора параллельного действия
Что такое сумматор
В общем смысле слова, сумматор – это какое-либо устройство, которое что-либо суммирует и выдает на выходе сумму этих воздействий. Сумматор можно представить в виде какого-либо неизвестного нам ящика, на который поступает входные воздействия и на выходе такого ящика выдается их сумма.
В электронике сумматоры делятся на две группы:
В этой статье мы будем разбирать аналоговые сумматоры.
Аналоговый сумматор
Многие помнят осциллограмму постоянного напряжения.
Если, допустим, цена нашего квадратика 1 В, то на данной картинке мы видим постоянное напряжение амплитудой в 1 В. Суммировать постоянное напряжение – одно удовольствие. Для этого достаточно сложить амплитуды этих сигналов в любой момент времени.
На рисунке ниже мы видим два сигнала A и B и сумму этих сигналов: A+B. Если сигнал A = 2 В, сигнал B = 1 В, то сумма этих сигналов составит 3 В.
Все то же самое касается и сигналов с отрицательной полярностью.
При сложении сигналов с равной амплитудой, но разной полярности, в сумме получаем 0. То есть эти два сигнала взаимно себя скомпенсировали: 1 +(-1)=0. Все становится намного веселее, если мы начинаем складывать сигналы, которые меняются во времени, то есть переменные сигналы. Они могут быть как периодические, так и непериодические.
Рассмотрим самый простой пример. Есть два синусоидальных сигнала с одинаковыми амплитудами, частотами и фазами. Подадим их на сумматор. Что получится в итоге?
В момент времени t1 у нас амплитуда сигнала А была равна 1 В, амплитуда сигнала В тоже 1 В.
В сумме их результат в момент времени t1 будет равен 2 В, что мы и видим на сигнале A+B
Если сместить фазу одного из сигналов на 180 градусов, относительно другого, а амплитуды и частоты сигналов оставить без изменения, то чему будет равняться их сумма? Сместим второй сигнал на 180 градусов и суммируем их амплитуды в каждый момент времени. Сумма будет равняться нулю, что и видно на рисунке ниже.
Сложение двух сигналов в Proteus
Если надо сложить в теории два каких-нибудь два сложных сигнала с разными фазами, амплитудами, частотами, то проще всего прибегнуть к различным симуляторам.
Один из них – это Proteus. С помощью него можно сложить два любых сигнала и посмотреть их сумму.
Для этого надо выбрать синусоидальный генератор.
Затем виртуальный осциллограф.
Задать параметры генератору.
Теперь можно сложить два синусоидальных сигнала с одинаковыми амплитудами, фазами и частотами.
Прописать амплитуду и частоту каждого сигнала и нажать «пуск».
Нажать правой кнопкой мыши на виртуальный осциллограф и нажать Digital Oscilloscope.
Для того, чтобы найти их сумму, достаточно нажать на кнопку A+B.
Получаем сумму двух сигналов.
В таком виртуальном осциллографе можно складывать любые два сигнала.