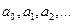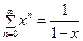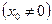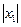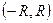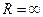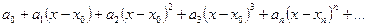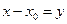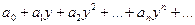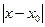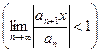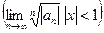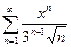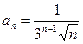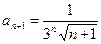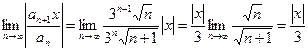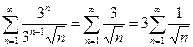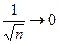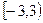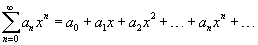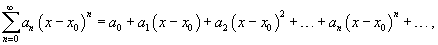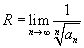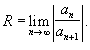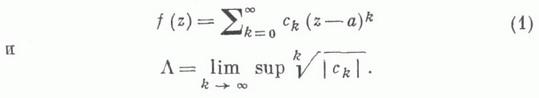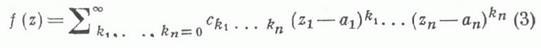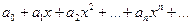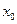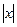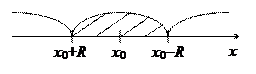что такое область сходимости степенного ряда
Степенные ряды
Функциональный ряд вида
Значит, ряд сходится при и расходится при 
.
Формула Коши Адамара получается применением признака Коши для положительных рядов к степенному ряду. Похожая формула для радиуса сходимости получается, если мы применим признак Даламбера к степенному ряду:
Итак, для определения области сходимости, нужно сначала определить радиус сходимости по одной из формул, а затем исследовать сходимость ряда в концах интервала сходимости. Для разложения произвольной функции в степенной ряд нужно знать определение ряда Тейлора и пять основных разложений.
Пять основных разложений:
Пример 4. Разложить функцию в ряд Маклорена и найти область сходимости.
Воспользуемся стандартным разложением:
Пример 5. Определить радиус сходимости ряда и исследовать поведение ряда на границе промежутка сходимости.Находим радиус сходимости. Используем вторую формулу:
Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.
Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.
Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.
Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).
В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.
В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.
Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.
Нужна помощь с курсовой или дипломной работой?
Степенные ряды
Содержание
Определение [ править ]
Лемма Абеля [ править ]
Вся теория степенных рядов основана на лемме Абеля.
[math]|a_n x_1^n| = |a_n x_0^n| \left(\frac<|x_1|><|x_0|>\right)^n[/math]
[math]\sum\limits_ Можно определить важнейшую для теории величину — радиус сходимости ряда. 1) [math]|x| \lt R[/math] [math]\Rightarrow[/math] ряд абсолютно сходится. 2) [math]\forall [a; b] \in (-R; R)[/math] ряд сходится абсолютно и равномерно. 3) [math]|x| \gt R[/math] [math]\Rightarrow[/math] ряд расходится. 4) [math]|x| = R[/math] — неопределённость. 2) [math]\exists \delta \gt 0 : [a; b] \subset [-\delta; \delta] \subset (-R; R)[/math] 3) Следствие определения радиуса сходимости. 4) Ну неопределённость [math]:)[/math] Докажем первый пункт. Второй доказывается аналогично. Рассмотрим [math]\sum\limits_ Итого: [math]|x| \lt q[/math] — ряд сходится, [math]|x| \gt q[/math] — ряд расходится. Второй пункт доказывается аналогично радикальным признаком Коши. По теореме о радиусе сходимости, на промежутке сходимости ряд сходится абсолютно. Если взять два степенных ряда, то на общей части их промежутка сходимости, ряды будут абсолютно сходиться, и, значит, с ними можно делать любые арифметические действия. В частности, их можно умножать по Коши: [math]f(x) g(x) = \sum\limits_ Вывод: произведение двух степенных рядов по правилу Коши — степенной ряд с суммой, равной произведению сумм исходных рядов. По теореме о радиусе сходимости, на любом отрезке из [math](-R; R)[/math] степенной ряд сходится равномерно. Значит, по теоремам о почленном дифференцировании и интегрировании рядов, их можно дифференцировать и интегрировать, и опять будет получаться сходящийся степенной ряд. Вопрос: «Каковы будут радиусы сходимости почленно проинегрированных или продифференцированных рядов?» Ответ: «Почленное интегрирование или дифференцирование не меняет радиуса сходимости ряда». Выясним, что для [math]f(x)[/math] и [math]f'(x)[/math] одинаковые радиусы сходимости. Поэтому, промежуток сходимости продифференцированного ряда [math]\subset[/math] промежутку сходимости исходного ряда. Перейдем к рассмотрению рядов, членами которых являются функции, в частности, степенные функции. Определение 1. Степенным рядом называется ряд вида: При а=0 степенной ряд примет вид: Определение 2.Совокупность значений x, при которых степенной ряд сходится, называется областью сходимостью степенного ряда. Пример. Найти область сходимости. Это геометрический рядq = x. Он сходится при Структура области сходимости степенного ряда устанавливается с помощью теоремы Н. Абеля: 1. Если степенной ряд (2) сходится приx = x0≠ 0, то он абсолютно сходится и при всех значениях x, удовлетворяет неравенству 2. Если степенной ряд (2) расходится приx = x1≠ 0, то он расходится и при всех значениях x, удовлетворяет неравенству Из теоремы Н. Абеля следует, что существует такое число R ≥ 0, что при всех Число Rназывается радиусом сходимости степенного ряда, а интервал (−R; R) называется интервалом сходимости. На концах интервала сходимости ряд (2) может, как сходится, так и расходится. Для ряда (1) получим: Радиус сходимости степенного ряда находится по формуле: Следовательно, (−2; 2) – интервал сходимости. При Следовательно,при Тогда (−1;1) – интервал сходимости. При x=1ряд расходится, как обобщенный гармонический. При x=−1 получим знакочередующийся ряд. На основании признака Лейбница он сходится, т.к. Следовательно, область сходимости −1≤x˂1 Пусть степенной ряд имеет интервал сходимости Тогдаряд, полученный из данного ряда почленным дифференцированием или интегрированием, имеет тот же интервал сходимости. Следовательно, на интервале сходимости степенные ряды можно почленно дифференцировать и интегрировать. Если функция Этот ряд называется рядом Тейлора. В частном случае при a=0 ряд примет вид: Этот ряд называется рядом Маклорена. Разложение в степенные ряды элементарных функций Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом: Часто рассматривается также ряд, расположенный по степеням (x − x0), то есть ряд вида где x0 − действительное число. Интервал и радиус сходимости Рассмотрим функцию или на основе признака Даламбера: пусть задан степенной ряд Если План лекции Лекция 6. Степенные ряды Озерная (лимническая) группа континентальных отложений Озерные отложения являются субаквальными образованиями, и те из них, которые образуются в крупных озерах, по своей характеристике стоят ближе к морским, чем к континентальным отложениям. Особенно это относится к таким обширным солоноватоводным замкнутым водоемам, как Каспийское или Аральское моря, осадки которых являются морскими. В лимническую группу не входят также осадки старичных озер речных пойм и временных озеровидных разливов, периодически возникающих по периферии крупных конусов выноса в аридных климатических обстановках. Они относятся, соответственно, к аллювию и пролювию и должны рассматриваться как их озерные фации. Отложения приледниковых озер выделяются в особую группу ледникового ряда. Такое ограничение лимнической группы отложений вносит в классификационную схему некоторую условность, т.к. все члены сложного континентального осадочного комплекса тесно взаимосвязаны. Характер озерных осадков в значительной степени определяется климатом, который влияет на гидрологию водоемов, гидрохимию вод и массу органического вещества, образуемого водными организмами. В пресноводных проточных озерах гумидных климатических зон накапливаются илы с железо-марганцевыми конкрециями (озерные руды), сапропели (торфянистые и водорослевые) и диатомиты. В солоноватоводных и соленых бессточных озерах аридных зон – биохемогенные карбонатные (известковые и доломитовые) илы и самоосадочные соли (гипс, мирабилит, поваренная соль). В засушливых условиях накапливаются хемогенные осадки. Но в одной и той же климатической зоне сосуществуют озера с разным составом осадков, зависящим от размеров и морфологии озерного водоема, площади, рельефа и геологического строения водосбора. Поэтому в разных озерах могут преобладать то песчано-алевритовые и глинистые осадки (особенно в горах), то чисто органогенные илы. Характер напластования и присутствие остатков диатомовых водорослей, пыльцы и спор высших растений делают некоторые разновидности озерных отложений важными объектами климатостратиграфических исследований. 6.1. Область сходимости степенного ряда 6.2. Разложение функций в степенные ряды 6.3. Применение степенных рядов в приближённых вычислениях Функциональный ряд вида называется степенным рядом, где постоянные числа Теорема Абеля. Если степенной ряд сходится в т. Из теоремы Абеля следует, что существует некоторый интервал Рассмотрим степенной ряд более общего вида Рис. 3. Интервал сходимости степенного ряда Для нахождения области сходимости степенного ряда удобно пользоваться признаками Даламбера Пример. Найти область сходимости степенного ряда Решение. Данный ряд является степенным, и Ряд сходится по признаку Даламбера, если Подставив х = 3 в исходный ряд, получим Этот ряд расходится как обобщённый гармонический со степенью Следовательно, областью сходимости данного ряда является полуоткрытый интервал Степенные ряды являются равномерно сходящимися. Поэтому на них распространяются свойства этих рядов. Ещё раз их перечислим. 1. Сумма степенного ряда есть функция, непрерывная в интервале сходимости ряда. 2. Степенной ряд можно почленно дифференцировать и интегрировать в интервале сходимости, и при этом полученные ряды имеют тот же интервал сходимости.[math]\triangleleft[/math] Радиус сходимости [ править ]
[math]\triangleleft[/math] Примеры [ править ]
Произведение степенных рядов [ править ]
Степенные ряды. Область сходимости. Теорема н. Абеля.
то есть при
или
следовательно, область сходимости (−1; 1).
.
.
ряд (2) сходится, а при
расходится.
, то есть 
.Следовательно, интервал сходимости ряда (1) имеет вид:
.
ряд расходится, так как
ряд расходится.
Свойства степенных рядов
.Ряд Маклорена. Ряд Тейлора.
разлагается в степенной ряд по степеням
, то ряд имеет следующий вид:
степенные ряды
. Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости. Если интервал сходимости представляется в виде 
, где R > 0, то величина R называетсярадиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно. Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле
то ряд (1) сходится только в точке z=a; если 
то ряд (1) абсолютно сходится в круге 
радиуса
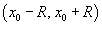
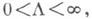
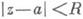
Область сходимости степенного ряда
являются коэффициентами степенного ряда.
. (5)
, то ряд сходится абсолютно для всех х, для которых 
.
с центром в т. х = 0, внутри которого ряд сходится абсолютно, а вне интервала – расходится. Этот интервал называется интервалом сходимости, а положительное число R – радиусом сходимости. Если ряд расходится при всех значениях х, кроме х = 0, то R = 0; если ряд сходится при всех значениях х (на всей числовой оси), то 
.
, из которого подстановкой 
можно получить приведённый выше ряд 
. Если радиус сходимости нового ряда равен R, то предыдущий сходится при всех х, для которых 
R ряд расходится.
или радикальным Коши 
. Из-за того, что члены функционального ряда при различных х могут быть как положительными, так и отрицательными, в пределах поставлены модули. При этом концы интервалов исследуются отдельно, так как на концах указанные пределы равны 1, и данные признаки ответа не дают.
.
, 
. Вычислим предел:
.
3 расходится. Концы интервала надо исследовать отдельно.
.
), и общий член ряда стремится к нулю при 
(
).
.