что такое нотация кнута
О действительно БОЛЬШИХ числах (часть 1)
В общем, как сказал IngvarrT в обсуждении статьи про числа-гиганты, весь дальнейший текст сводится к фразе «Прикиньте, шо придумали математики».
Все мы знаем три основные арифметические операции: сложение (a+b), умножение (a × b), возведение в степень (a b ). Никогда не задумывались, что все эти операции последовательно вытекают одна из другой? А если так:
Обобщенно эти операции называются гипероператорами. Для сложения, умножения и возведения в степень — 1-го, 2-го и 3-го порядка соответственно. Продолжение этого ряда на более высокие порядки напрашивается само собой: гипероператором 4 порядка (тетрацией) называют последовательное возведение в степень:
А вот для гипероператоров более высоких порядков использовать такую систему обозначений уже не получится — уж больно громоздкими и запутанными будут степенные башни. Поэтому для обозначение больших чисел используются другие системы нотаций.
Одной из наиболее распространенных является стрелочная нотация Дональда Кнута, предложенная в 1976 году. Принцип записи чисел вытекает из последовательности гипероператоров и по большому счету представляет собой явное указание порядка гипероператора. Обычное возведение в степень (гипероператор 3 порядка) обозначается одной стрелкой: a↑b, тетрация — двумя стрелками a↑↑b и так далее. Вот как вычисляется тетрация: 
Изменив всего одну цифру мы получаем гигантский рост значения числа:

Добавив еще одну стрелку мы получаем гипероператор 4 порядка — пентацию:

Изменение одной цифры здесь приводит к столь большому росту значения, что эпитеты можно и не подбирать:

(это число назвается тритри, и оно нам еще пригодится)
Чтобы не рисовать много стрелок, используется сокращенная запись: a↑ n b для обозначения a↑↑. ↑b с n стрелок.
Решением проблемы нотации Кнута являются цепочки Конвея. Они используются тогда, когда для записи числа даже стрелочная нотация Кнута становится слишком громоздкой. Помните про число Грэма, которое упоминалось в самом начале? Обозначить его стрелками Кнута просто невозможно. Определение цепочки и её взаимосвязь со стрелочками Кнута:

Вроде бы всё одно и то же. Но проблема «количества стрелочек» в цепочках Конвея решается легко и изящно: добавлением еще одной стрелки. А каждая стрелка обращает всю предыдущую цепочку на себя. Попробуем разобраться на примере: возьмем тетрацию 3 → 3 → 2 (что это такое: берем первые два числа и проделываем операцию возведения в степень три раза), добавим справа → 2.
3 → 3 → 2 → 2 = 3 → 3 → ( 3 → 3 → 1 → 2) → 1 = 3 → 3 → (3 → 3) = 3 → 3 → 27
Добавив всего однy стрелочку мы сразу перешли к гипероператору 27 порядка. И число Грэма, никак не представляемое в стрелочной нотации Кнута, цепочками Конвея записывается очень лаконично: 3 → 3 → 64 → 2. А ведь можно продолжать добавлять стрелочки и переходить ко всё более невообразимым порядкам чисел.
Ха! Но разве это правильно, рисовать столько стрелок? Да и слишком уж ме-е-едленно растут числа… В общем, Джонатан Бауэрс ввел массивную нотацию (array notation), которая в своей максимально расширенной форме называется BEAF (Bowers Exploding Array Function, взрывная массивная функция Бауэрса, игра слов с английским beaf — говядина. Надо отметить, что Бауэрс даже в своих научных трудах отличается особым чувством юмора). Запись ее очень проста и напоминает уже рассмотренные нотации: 3↑↑↑3 = 3 → 3 → 3 = <3,3,3>. Используется также другая система массивной нотации, когда последний элемент, обозначающий порядок гипероператора, переносится в середину записи, т.е. <3,3,2>= 3 <2>3 (логика такая — берем две цифры по краям и делаем с ними то, что указано в середине).
На данном этапе никаких отличий массивной нотации от цепочек Конвея нет. Но добавление четвертого элемента массива имеет принципиально другой смысл, а именно — количество скобочек: <3,3,3>= <3,3,3,1>, <3,3,3,2>= <<3,3,3>>.
Для наглядности посмотрим, что происходит при изменении элемента внутри центральных скобочек «всего на единицу»:
<3,3,1,2>= 3 <<1>> 3 = 3 <3 <3>3> 3 = <3, 3, <3, 3, 3>> = <3, 3, тритри>
<3,3,2,2>= 3 <<2>> 3 = 3 <<1>> 3 <<1>> 3 = <3, <3, 3, тритри>, 1, 2> = 3 <3 <3… 3 <3>3> 3… 3> 3> 3, где количесто троек, расходящихся от центра к краям, равно <3,3, тритри>.
В сравнение с цепочками Конвея взрывной рост числа происходит на этап раньше — если у Конвея лишь четвертое число обращает все предыдущие операции на себя, то у Бауэрса — уже третье. Яркий пример с рассмотренными выше числами:
у Конвея третья единица «съедает» остаток цепочки 3 → 3 → 1 → 2 = 3 → 3 = 27, то у Бауэрса она как раз «работает» на дальнейший его рост: <3,3,1,2>= <3,3, тритри>.
Кстати, это был всего лишь массив из 4 элементов. Добавим безумия? Просто увеличивать количество элементов массива через запятую, следуя уже сформулированным правилам работы с ними — это неинтересно. Поэтому Бауэрс придумывает видоизмененные «скобки» для того, чтобы хоть минимально наглядно «представить» числа в массивной нотации. Четвертое число в массиве еще остается с фигурными скобками, а дальше начинается форменное безобразие: пятое — квадратные скобки, повернутые на 90 градусов, шестое — кольца вокруг предыдущей конструкции, седьмое — обратные угловые скобки, восьмое — как трехмерные квадратные… Короче, проще это показать: 
(еще на подобные картинки можно посмотреть здесь)
Вы думаете, что Бауэрс на этом остановился? Как бы не так. Ну вот что, ЧТО еще можно придумать в записи массивов? А можно обратить внимание, что там есть запятые… Которые пусть обозначают элементы одномерного массива. А если поставить между числами (1), то это переход на следующую строку, (2) — переход на следующую плоскость.
Квадрат из троек («дутритри») записывается как <3,3,3(1)3,3,3(1)3,3,3>.
Куб из троек («диментри») — <3,3,3(1)3,3,3(1)3,3,3(2)3,3,3(1)3,3,3(1)3,3,3(2)3,3,3(1)3,3,3(1)3,3,3>.
Вот так незатейливо мы перешли от плоскостных массивов к объемным (и заметьте, это всего лишь запись некого числа, которая из-за своих масштабов потребовала выйти из плоскости просто в своем написании!). Разумеется, дальше мы вводим новые обозначения для четырехмерных, пятимерных «объектов» (простите, называть эти монструозные контрукции числами уже сложно). Например, & означает «массив из»: <10,100,2>& 10. То есть <10,100,2>-массив десяток, или же 10↑↑100-массив десяток. Ну то есть нужно 100 раз возвести десять в десятую степень, построить решетку с таким количеством ячеек (причем она будет находиться в стозмерении, то есть измерении измерений измерений… измерений (слово повторено сто раз)), затем заполнить все ячейки десятками — и только тогда можно приниматься решать этот массив.
Думаете хотя бы на этом всё? Неа. Обозначим «легион» прямым слэшем (/). В массиве
Еще одно расширение Бауэрс сделал добавив символ @ (a@b обозначает «легионный массив размера a из b») и обратный слэш \ (лугион). Ну тут уже всё понятно:
Понятно, что процесс придумывания новых наименований для каких-то операций не может быть бесконечным (за легионами и лугионами идут лагионы, лэгионы и лигионы, но очевидно, что это ничто, учитывая наш размах), поэтому Бауэрс сделал проще — определил L как прогрессию из легионов, лугионов, лагионов, лэгионов и лигионов: L1, L2, L3… И далее число опередляется индексами.
Например для «вычисления» (смешно, конечно, говорить о вычислениях на таких масштабах)
Кстати, для 340 больших чисел Бауэрс ввел собственные наименования, многие из которых по своей безумности полностью соответствуют алгоритмам расчета. Встречайте, МЕАМЕАМЕАЛОККАПУВА УМПА: <
Как уже говорилось выше, BEAF по своей мощи значительно превосходит цепочки Конвея, не говоря уже о нотации Кнута… Интересно, что дальше?
А дальше мы вступаем на поле скорее философии, нежели собственно математики. Все описанные выше нотации представляют собой вычислимые функции или функции, которые могут быть реализованы на машине Тьюринга.
Во второй части мы рассмотрим невычислимые функции: задачу усердных бобров, сигма-функцию Радо Σ(n), число Райо, BIG FOOT и другие, а также рассмотрим быстрорастущую иерархию, чтобы понять, есть ли предел этому математическому безумию.
Рональд Грэм, друг Бесконечности
Для своего времени (1977 год) и на протяжении многих лет это было самое больше число, использованное в математическом доказательстве.
И тем число Грэма ещё восхитительней, что для его понимания не нужно обладать специальным математическим образованием. Его может понять и испытать невероятный душевный трепет самый обычный человек с элементарными знаниями и хорошим творческим мышлением. Я это докажу.
Число Грэма настолько велико, что для него бессмысленны такие эпитеты как «огромное», «гигантское», «сверх-гигантское», «колоссальное», «чудовищное» и так далее. Любые определения превосходных категорий крайне убоги на фоне этого числа, поэтому мы сразу же успокоимся и для простоты назовём его просто: «Очень Большое число».

Число Грэма не имеет эквивалента в физическом мире, его невозможно отобразить предметно и даже вообразить в объеме чего-либо.
Это не количество песчинок в пустыне Сахара и всех остальных пустынь, не количество молекул воды в Мировом океане и не количество атомов во всей наблюдаемой Вселенной (≈10 80 ).
Как первое, так второе и третье, как бы это выразиться. ну скажем: ничтожное чуть более, чем ничто по сравнению с числом Грэма.
Более того, если представить, что существует столько других Вселенных, сколько атомов в нашей Вселенной, и в каждой из них тоже столько же атомов, сколько в нашей, и если все атомы этой Мультивселенной взять вместе – то это тоже будет чуть более, чем ничто по сравнению с числом Грэма.
Это выходит, что 10 80 нужно умножить на 10 80 – при умножении с одинаковыми основаниями показатели степени просто складываются, а основание остаётся неизменным: получится 10 160 – невидимая пыль в масштабе числа Грэма.
Можно в буквальном смысле всю жизнь сидеть и придумывать Мультивселенные мультивселенных, складывать и перемножать их атомы, но результатом будет все тот же: ничтожное чуть более, чем ничто по сравнению с числом Грэма.
Ну мы гугол даже рассматривать не будем в масштабе числа Грэма, эту станцию мы давно проехали. Но есть такое число как гуголплекс – десять в степени гугол.
Впечатляет, да? Цифру 10 нужно перемножить гугол раз. Гуголплекс нельзя записать в десятичной системе. Потому что придется написать цифру 1, а после неё гугол нулей. Понимаете? Не миллиард нулей написать после цифры 1, не триллион нулей, не дециллион, а гугол нулей!
Но у нас во Вселенной атомов меньше, чем гугол, как мы помним!
То есть если даже мы решим, что каждый атом – это отдельная цифра – «1» и «0», то их не хватит, чтобы записать гуголплекс! Да на чём писать-то?! На производство бумаги уже ничего не останется во Вселенной.
Поэтому гуголплекс можно записать только в виде степени, как показано выше.
Большое число гуголплекс? Оооочень большое!
А по сравнению с числом Грэма? Гм. ничтожное чуть более, чем ничто. Простите!
А гуголплекс в степени гуголплекс? Может уже близко к числу Грэма?
Ничтожное чуть более, чем ничто.
А гуголплекс в степени гуголплекс в степени гуголплекс в степени гуголплекс в степени гуголплекс – и так гуголплекс раз?! Ничтожное чуть более, чем ничто.
Я сильно понижу планку сравнений, потому что говорил о вещах абстрактных с крайне малым индексом воображения. А представьте себе обычную пшеничную муку. У каждого на кухне есть. Если набить пшеничной мукой под завязку нашу Вселенную, как мешок размером в 93 миллиарда световых лет, то будет слишком нелепо сравнивать количество крупинок муки с числом Грэма. Слишком нелепо! Число Грэма больше в невообразимое количество раз.
Я понимаю: рассуждения кажутся густо заливистыми и мошенническими – ну разве может такое быть, чтобы число атомов вселенных и мультивселенных, гуголплексы в степени гуголплексов – и всё это ничтожное?! – может, автор чеканулся?! – но когда вы позже поймёте число Грэма, сомнения развеются.
Но достаточно лирики в отношении предмета, перейдём к прозаическому его разъяснению. Конечно, я наговорил о нём предостаточно необъятно-возвышенного. Однако, с помощью особой записи, которую можно понять и без математического образования, вы осознаете если не масштаб числа Грэма (это невозможно), но хотя бы ухватите рассудком крупицу числа Грэма, затмевающую Вселенную.
Природа числа
Эту главу можно не читать, здесь просто объясняется, как Грэм пришёл к своему числу.
Важно понимать: число Грэма – это не просто выдуманная от нечего делать величина в математике, выдумать-то можно, что угодно. Оно не символическая абстракция, а прикладной инструмент. Число Грэма – доказательство в решении математической задачи.
Сама задача из области математики под названием комбинаторика. Тоже можно понять без специального образования. Я понял, поймете и вы.
Напишу предельно простым языком, не употребляя такие слова как «графы» и «подграфы»
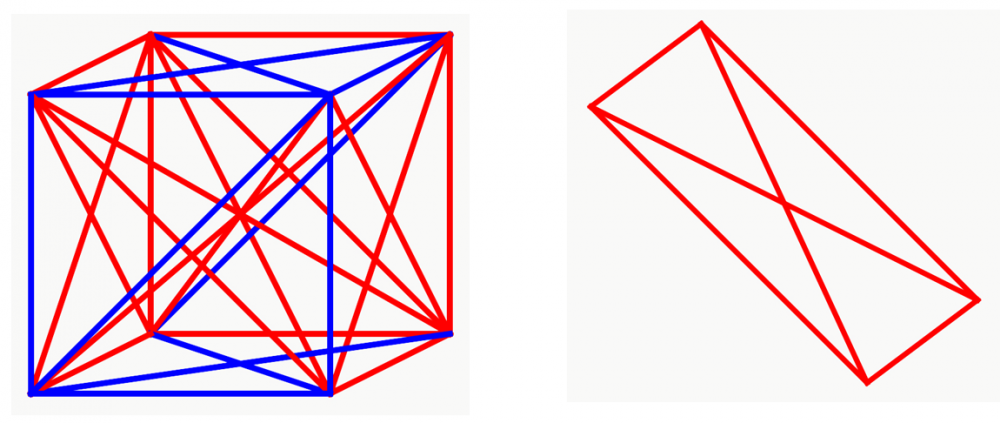
В общем так: у нас есть трехмерный куб. Все его вершины соединены линиями двух цветов – синего и красного. В произвольном порядке (но из каждой вершины должна исходить хотя бы одна линия другого цвета).
Можно распределить цвета так, что внутри куба получатся линии только одного цвета и лежащие в одной плоскости.
Как на рисунке справа.
Этакий красненький «андреевский» флаг или «почтовый» конвертик, как кому нравится. Но можно по-другому распределить цвета, и они не будут одного цвета в одной же плоскости – закрасить, например, одну линию «конвертика» синим.
А в четырехмерном кубе – тессеракте – можно тоже два варианта? Да, можно.
А в пятимерном? Да, можно.
В общем, математики дошли до шестимерного куба, и там всё также срабатывали оба варианта: можно и с одноцветным «конвертиком», и без него разукрасить.
На этом они остановились, потому что дело было в 70-х, и это был предел математических способностей того времени.
Но, конечно же, учёных продолжал безумно волновать вопрос: какой минимальной размерности должен быть куб, чтобы ИЗБЕЖАТЬ одноцветных линий в одной плоскости было НЕЛЬЗЯ?!
«Сколько-мерный» куб должен быть построен, когда как ни старайся, как ни комбинируй цветные линии, одноцветный «конвертик» обязательно будет наличествовать?!
Рональд Грэм предложил сокрушительный метод решения задачи: он доказал, что та самая размерность находится между цифрой 6 и неким Большим числом, которое он предложил. Может, уже семимерный куб даст неизбежный одноцветный «конвертик», а может, предпоследнее число перед Большим числом – где-то между ними – обязательно.
Проще говоря: Большое число – верхний предел размерности куба. Впоследствии это Большое число и назвали числом Грэма.
Кстати, в наше время нижняя граница поднялась повыше: до 13-мерного куба рассчитали математики – нет ещё обязательного одноцветного «конвертика»)))
Да, вы, конечно, можете поинтересоваться: «А почему они это делают, Грэм и другие?! Строят кубы, разрисовывают квадратики, ищут плоскости? Кому это надо вообще?!» Конечно, конечно. Но давайте так: две с половиной тысячи лет назад подобные вопросы задавали Пифагору и Евклиду их незатейливые современники, а вон оно как вышло. Не уподобляйтесь незатейливым современникам.
Приступим к осознанию числа Грэма.
Тройка
Нам понадобится цифра «3», которая должна быть возведена в Очень Большую Степень.
Но как я уже сказал, число Грэма нельзя записать не только в десятичной системе, но даже в виде степени это сделать невозможно. Однако, в семидесятых годах другой математик по имени Дональд Кнут разработал метод записи Больших чисел, который после назвали стрелочная нотация Кнута. Очень красиво звучит. Даже поэтически.
Я не буду разъяснять отдельно, что такое стрелочная нотация Кнута, чтобы не перегружать. Вы поймёте этот метод по ходу осознания числа Грэма. Также я не буду использовать особые термины (тетрация, пентация и гексация) с той же целью: не утяжелять восприятие. Как говорил Эйнштейн, нужно упрощать всё до предела, но не более того.
Итак, первый уровень:
«Одна стрелка»
Одна стрелка в нотации Кнута означает простое возведение цифры в какую-либо степень: 2↑4 = 2 4 = 16; 5↑3 = 5 3 = 125; 10↑5 = 10 5 = 100 000
Но у нас в основе цифра «3».
Всё просто! Пока всё очень просто.
Переходим на второй уровень.
«Две стрелки»
Тут тоже всё достаточно просто. При двух стрелках в нотации Кнута число справа указывает, в каком количество будет представлено число, которое находится слева, при горизонтальной развёртке записи «две стрелки» в запись «одна стрелка» – упрощаем.
Справа у нас цифра «3». И слева, так получилось, что она же.
Таким образом 3↑↑3 = 3↑3↑3 – и мы получаем последовательное возведение в степени троек.
Важно. Вычисление в стрелочной нотации Кнута производится справа-налево.
– это не 27↑3 = 27 3 = 19 683! – неправильно!
3↑↑3 = 3↑3↑3 = 3↑27 = 3 27 = 7 625 597 484 987!
Всего две стрелки в нотации Кнута и уже более 7 с половиной триллионов!
Но это ещё не всё. Нам придётся задержаться на уровне «две стрелки» и ввести такое понятие как «степенная башня», потому что дальше нам без него не обойтись.
Итак, возвращаемся к записи «две стрелки»: 3↑↑3
Схема построения степенной башни такая же, как при горизонтальной развёртке. Проще говоря, степенная башня – это вертикальная развёртка нотации Кнута.
Число справа указывает, в каком количестве будет представлено число, которое находится слева, при вертикальной развёртке:
– у нас получилась степенная башня!
Важно. Результат степенной башни вычисляется сверху-вниз!
То есть самое верхнее число обозначает степень, в которую нужно возвести число ниже, результат сам становится степенью, в которую нужно возвести число ниже. И так далее до самого нижнего числа.
3↑↑3 = 3 3 3 = 3 27 = 7 625 597 484 987
– как и при горизонтальной развёртке! Ну надо же – один результат )
Чтобы вы понимали: если бы справа была цифра «5», то развёртка выглядела бы так: 3↑↑5 = 3↑3↑3↑3↑3 – пять троек. И степенная башня состояла бы из пяти троек, и башню нужно было бы вычислять сверху вниз. Число уже огромное, позже придём к нему.
Думаю, всё понятно с двумя стрелками. Переходим на следующий уровень.
«Три стрелки»
Тут сложнее, но всё равно ещё доступно для быстрого понимания.
Применяем метод горизонтальной развёртки при трёх стрелках. Число справа указывает, в каком количестве будет представлено число слева, при горизонтальной развёртке записи «три стрелки» в запись «две стрелки».
Тогда 3↑↑↑3 = 3↑↑(3↑↑3) – три тройки, а между ними по две стрелки.
Берём развёртку в «две стрелки» и вычисляем правую часть, которая в скобках:
. (3↑↑3) – скобки и вставлены для того, чтобы показать очередность вычислений.
Это простая запись в «две стрелки», которую мы уже вычислили выше в виде горизонтальной развёртки в три тройки справа-налево и в виде степенной башни в три тройки же сверху-вниз, и у нас получилось 7 625 597 484 987.
Тогда подставляем это число вместо троек с двумя стрелками в скобках:
3↑↑↑3 = 3↑↑7 625 597 484 987
Как мы прекрасно помним, в записи «две стрелки» число справа указывает, в каком количестве будет представлено число, которое находится слева, при горизонтальной развёртке записи «две стрелки» в запись «одна стрелка».
3↑↑↑3 = 3↑↑7 625 597 484 987 = 3↑3↑3↑3. 3↑3↑3↑3
– и количество троек, между которыми будет «одна стрелка», будет равняться числу 7 625 597 484 987!
То есть цифры «3» нужно последовательно возвести в непомерно возрастающие степени, вычисляя справа-налево – когда результат вычисления справа становится степенью для тройки левее и так далее – 7 625 597 484 987 раз!
Или можно создать вертикальную развёртку и построить «степенную башню», при которой цифра «3» вытянется лестницей степеней в количестве 7 625 597 484 987 раз!
Если каждую тройку записывать в тетрадную клеточку, то высота такой башни составит примерно 38 миллионов километров – это расстояние до планеты Венеры.
Важно. Степенная башня высотой до Венеры – это не число с таким количеством цифр – да, оно тоже было бы гигантским! А это именно что степенная башня, которую нужно ещё вычислять, чтобы получить конечный результат в виде числа. И вычислять нужно, как мы помним, сверху-вниз!
Так вот если мы представим, что на Венере существует какая-то древняя могущественная цивилизация, и один из её представителей возьмётся для нас вычислить степенную башню в 7 625 597 484 987 троек, то он будет спускаться по ней как по лестнице.
Первая ступенька – 3.
Вторая ступенька – 27.
Третья ступенька – 7 625 597 484 987
Четвёртая ступенька – 3 7 625 597 484 987 – понятия не имею, сколько это будет, вычислить уже нельзя подручными мощностями. Только супер-компьютер справится.
Пятая ступенька – 3 3 7 625 597 484 987 – тройка в степени тройки, которая сама в степени более 7 с половиной триллионов!
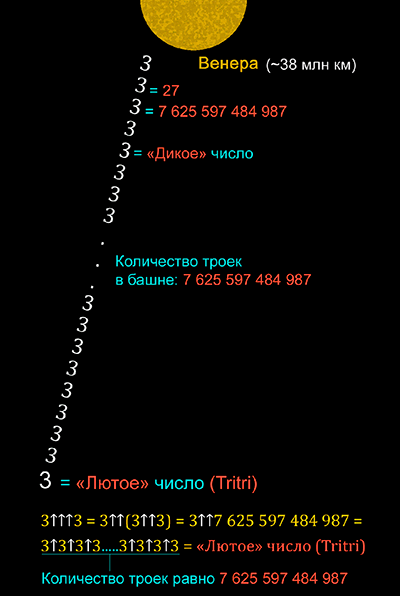
Гуголплекс побледнел перед ним и рассыпался. Это какое-то «Дикое» число! И оно всего лишь на пятой ступеньке вниз! А их там. ещё более
7 с половиной триллионов ступенек-троек! И каждая нижняя возводится в степень числа, которое получилось при вычислении верхней предыдущей.
Это – чудовищно-взрывная прогрессия.
Мы понятия не имеем в какую степень должна быть возведена самая нижняя ступенька-тройка, равно как понятия не имеем, каков будет результат – что это будет за конечное число в вычислении степенной башни?!
Но допустим, представитель древней могущественной венерианской цивилизации справился с вычислением. И не имея возможности назвать его нам, потому что в человечьем языке нет таких слов и масштабов в сознании, венерианец ограничился образным определением и назвал его «Лютое» число.
В земном научном мире у него, правда, есть название – «Tritri» («Тритри»).
Итак: 3↑↑↑3 = 3↑↑(3↑↑3) = 3↑↑7 625 597 484 987 = Лютое число (Tritri)
И для большей наглядности я нарисовал инфографику.
Переходим на следующий уровень.
«Четыре стрелки»
Я бы хотел написать «а вот это уже сложно», но если вы поняли предыдущие вычисления, то нет! Не сложно, хоть и массивней.
Применяем метод горизонтальной развёртки по прежнему алгоритму: в записи «четыре стрелки» число справа указывает, в каком количестве число слева будет представлено при переводе в запись «три стрелки»:
Мы её вычислили выше. И у нас получилось Лютое число или Тритри.
Подставляем его в горизонтальную развёртку:
Смотрим опять на нотацию «три стрелки»:.
Мы помним, что при записи «три стрелки» число справа указывает, в каком количестве число слева будет представлено в горизонтальной развёртке при переводе в запись «две стрелки». А справа у нас – Лютое-Тритри число.
. 3↑↑↑Лютое-Тритри = 3↑↑(3↑↑(3↑↑(3. (3↑↑(3↑↑(3↑↑3)) – таким образом мы видим, что при переводе записи «три стрелки» в запись «две стрелки» количество троек, между которыми «две стрелки», будет равняться. Лютому-Тритри числу!
Значит, в целом получается, что:
3↑↑↑↑3 = 3↑↑↑(3↑↑↑3) = 3↑↑↑Лютое-Тритри = 3↑↑(3↑↑(3↑↑(3. (3↑↑(3↑↑(3↑↑3)) – таким образом выходит, что в нашем случае нотация «четыре стрелки» разворачивается в конечном итоге в нотацию «две стрелки», где количество троек будет равняться Лютому-Трири числу. Скобки поставлены для того, чтобы обозначить первоочерёдность вычисления – справа-налево.
Значит, можем исключить из записи нотацию «три стрелки» – она своё отработала, и упростить нотацию «четыре стрелки».
– где количество троек в нотации «две стрелки» – Лютое-Тритри. Скобки я тоже убрал, чтобы не смущали.
Нет никакого смысла пытаться представить длину этой цепочки.
Идём дальше и метод горизонтальной развёртки дополняем вертикальными развёртками – степенными башнями.
Мы помним, что запись «две стрелки» означает, что число справа указывает, в каком количестве будет представлено число слева при вертикальной развёртке, то есть при построении степенной башни.
И у нас тут Лютое-Тритри число троек с «двумя стрелками», которые взаимосвязаны в цепочке горизонтальной развёртки.
Начинаем строить в горизонтальной развёртке степенные башни и вычислять сверху-вниз, двигаясь справа-налево.
Тогда строим башни и вычисляем, начиная с крайних справа троек:
= 3↑↑3↑↑3↑↑3. 3↑↑3↑↑3↑↑7 625 597 484 987
Получается, что тройка левее должна вырасти в степенную башню, состоящую аж из 7 625 597 484 987 троек – до Венеры, помните! Я её нарисовать уже не могу тут)
И когда мы вычислим эту башню сверху-вниз, то получим наше старое доброе Лютое-Тритри число!
А следующая тройка левее должна, соответственно, вырасти в степенную башню, состоящую и Лютого-Тритри числа троек! И когда мы вычислим эту степенную башню сверху-вниз, то получим число, назовём его Лютое-1.
А следующая тройка левее должна вырасти в степенную башню, состоящую из Лютого-1 числа троек. И так далее! – мы должны двигаться левее-левее-левее. – сверхчудовищная, сверхвзрывная прогрессия от башни к башне.
И всего троек-башен у нас, как мы помним, в цепочке горизонтальной развёртки Лютое-Тритри число (учитывая, что самая права тройка – тоже башня, маленькая такая, из одной цифры).
Помним: каждая башня левее состоит из количества троек, полученного при вычислении числа предыдущей башни, которая справа.
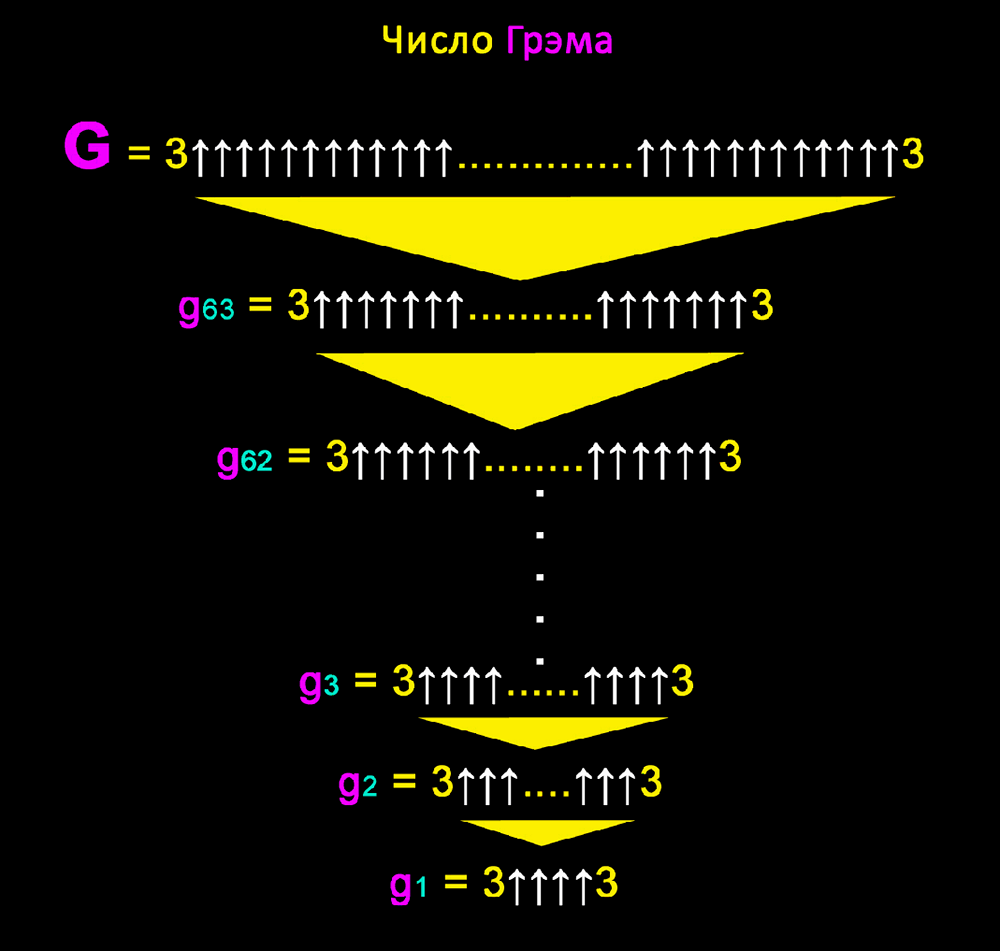
Таким образом, когда последняя тройка слева вырастит в башню, состоящую из невообразимого числа троек, полученного при вычислении предпоследней башни; и когда мы вычислим последнюю башню, то мы получим совершенно «Жуткое» число. Или как оно называется по-научному – g1.
Для простоты понимания смотрите инфографику.
Я, конечно, тут разошёлся малость – «вычислим Лютое число, вычислим Лютое-1 число, вычислим число g1!» – смешно!
Если помните, то Лютое-Тритри нам вычислил венерианец. Сами мы не вычислим ничего. Это абсолютно невозможно.
Жуткое-g1 число – запредельно, оно за гранью всех мыслимых и немыслимых Вселенных и Мультивселенных.
И это уже число Грэма? Гм. Честно сказать: не совсем )
Давайте снова маленькое лирическое отступление.
Знаете, есть такая наука палеонтология – изучение древней жизни на Земле. В нашем случае проще говоря – динозавров. Известно, что многие из них были большими и очень большими животными. Но целиком окаменелый скелет обнаружить очень трудно. Палеонтологи чаще всего находят фрагменты, например, уцелевший позвонок аргентинозавра или амфицелия, например. И учитывая размер позвонка – 1,8 – 2,5 метров высоту, прикидывают габариты животного в целом – получается внушительно: 40 – 50 метров в длину.
Так вот Жуткое-g1 число – это фрагмент числа Грэма, но! – с небольшими поправками. Всё-таки позвонок динозавра – довольно крупный фрагмент динозавра.
А g1 – как бы это сказать, не очень крупный фрагмент числа Грэма.
Это не только не позвонок, но и даже не клетка числа Грэма. А уж если быть совсем точным – это даже не атом числа Грэма.
g1 – запредельное гигантское, невообразимое число – это какая-то субатомная, запредельно маленькая частица числа Грэма, неразличимая в масштабе его тела целиком никоим образом. Никоим!
Проследим ещё раз наш путь:
3↑↑3 = 7 625 597 484 987
3↑↑↑3 = Лютое-Тритри число
3↑↑↑↑3 = Жуткое-g1 число
Понимаете, что всего четыре шага – от одной стрелки до четвёртой включительно – и мы получили феноменальную прогрессию от числа 27 до Жуткого-g1 числа.
Всего четыре стрелки!
Но вслед за g1 идёт g2 число.
Что оно из себя представляет?
Да это очень просто:
g2 = 3↑↑↑↑↑↑. ↑↑↑↑↑↑↑3 – где количество стрелок равно. g1. Это мучительно больно!
Понимаете, да?! «Четыре стрелки» катастрофическим образом разнесли наше представление о размерности и масштабах в виде необъятного числа g1.
И следующий уровень – это «g1 стрелок», которые нужно поместить между двумя тройками.
В результате мы получим число g2. То есть никогда мы ничего не получим, это я просто так говорю – образно, поэтически)))
А после g2 идёт число g3. Что это такое? Тоже просто:
g3 = 3↑↑↑↑↑↑. ↑↑↑↑↑↑↑3 – где количество стрелок равно. g2.
g4 = 3↑↑↑↑↑↑. ↑↑↑↑↑↑↑3 – где количество стрелок равно. g3.
g5 = 3↑↑↑↑↑↑. ↑↑↑↑↑↑↑3 – где количество стрелок равно. g4.
g63 = 3↑↑↑↑↑↑. ↑↑↑↑↑↑↑3 – где количество стрелок равно. g62.
И наконец 64-й слой:
g64 = 3↑↑↑↑↑↑. ↑↑↑↑↑↑↑3 – где количество стрелок равно. g63.
и привет Бесконечности! )
А есть ли число больше, чем число Грэма, которое также применялось в математическом доказательстве?
И называется это число TREE(3) – ДЕРЕВО(3)
И о нём как-нибудь в другой раз )
Конечно же, число Грэма – вымышленный персонаж физико-математического мира. Но так получилось, что многие персонажи этого мира – хоть вымышленные, хоть нет – производят несоизмеримо большее драматическое впечатление, чем любые вымышленные персонажи из лирико-художественного мира. Просто мало кто об этом задумывается.