что такое нетривиальное кольцо
Тривиальное кольцо
Важнейшими из таких объектов являются:
Всякая нулевая алгебра также тривиальна как кольцо. Нулевая алгебра над полем является нулевым линейным пространством, а над кольцом — нулевым модулем.
Содержание
Трактовка при помощи теории категорий
С точки зрения теории категорий, тривиальный объект является терминальным, а иногда (в зависимости от определения морфизма) нулевым (то есть одновременно терминальным и начальным) объектом.
Тривиальный объект единственнен с точностью до изоморфизма.
| 2 ↕ | [ 0 0 ] <\displaystyle <\begin | = | [ ] <\displaystyle <\begin | [ ] | ‹0 |
| ↔ 1 | ^ 0 | ↔ 1 | |||
| Элемент нулевого пространства, записанный как пустой вектор-столбец (справа), умножен на пустую матрицу 2×0 для получения 2-мерного нулевого вектора (слева). Правила умножения матриц соблюдены. | |||||
Структуры с единицей
В категории Ring колец с единицами, кольцо целых чисел Z является начальным объектом, а не <0>.
Теорема 1. Нетривиальное коммутативное кольцо К с единицей является целостным тогда и только тогда, когда в нем выполнен закон сокращения



Нетривиальное коммутативное кольцо К с единицей является целостным тогда и только тогда, когда в нем выполнен закон сокращения
ab = ac, a 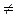
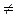
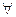
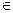
В самом деле, если в К имеет место закон сокращения, то из
аb = 0 = а0 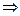
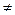
Обратно: если К область целостности, то
Например, в кольце Мn обратимый элемент это в точности матрицы с отличным от нуля определителем.
Обратный элемент a не может быть делителем 0
Инструменты пользователя
Инструменты сайта
Содержание
Кольцо (математика)
Кольца являются основным объектом изучения теории колец — крупного раздела общей алгебры, в котором разработаны инструментальные средства, нашедшие широкое применение в алгебраической геометрии, алгебраической теории чисел, алгебраической
История
Определение
Кольца могут обладать следующими дополнительными свойствами:
Простейшие свойства
Непосредственно из аксиом кольца можно вывести следующие свойства:
Основные понятия
Виды элементов кольца
Пусть в кольце есть элементы, отличные от нуля (кольцо не является тривиальным). Тогда левый делитель нуля — это ненулевой элемент кольца для которого существует ненулевой элемент кольца такой что Аналогично определяется правый делитель нуля. В коммутативных кольцах эти понятия совпадают. Пример: рассмотрим кольцо непрерывных функций на интервале Положим тогда то есть являются делителями нуля. Здесь условие означает, что является функцией, отличной от нуля, но не означает, что нигде не принимает значение 8)
Идемпотентный элемент — это такой элемент, что Например, идемпотентен любой оператор проектирования, в частности, следующий: в кольце матриц 10)
Если – произвольный элемент кольца с единицей то левым обратным элементом к называется такой, что Правый обратный элемент определяется аналогично. Если у элемента есть как левый, так и правый обратный элемент, то последние совпадают, и говорят, что обладает обратным элементом, который определён однозначно и обозначается Сам элемент называется обратимым элементом. 11)
Подкольцо
Подмножество называется подкольцом если само является кольцом относительно операций, определенных в При этом говорят, что – расширение кольца 12) Другими словами, непустое подмножество является подкольцом, если
По определению, подкольцо непусто, поскольку содержит нулевой элемент. Нуль и единица кольца являются нулем и единицей любого его подкольца. 13)
Подкольцо наследует свойство коммутативности. 14)
Пересечение любого множества подколец является подкольцом. Наименьшее подкольцо, содержащее подмножество называется подкольцом, порождённым а — системой образующих для кольца Такое подкольцо всегда существует, так как пересечение всех подколец, содержащих удовлетворяет этому определению. 15)
Подкольцо кольца с единицей порождённое его единицей, называется наименьшим или главным подкольцом кольца Такое подкольцо содержится в любом подкольце кольца 16)
Идеалы
Непустое подмножество кольца называется левым идеалом, если:
Из первого свойства следует и замкнутость I относительно умножения внутри себя, так что I является подкольцом.
Аналогично определяется правый идеал, замкнутый относительно умножения на элемент кольца справа.
Двусторонний идеал (или просто идеал) кольца — любое непустое подмножество, являющееся одновременно левым, так и правым идеалом.
Также идеал кольца может определяться как ядро некоторого гомоморфизма 18)
Идеал кольца, не совпадающий со всем кольцом, называется простым, если факторкольцо по этому идеалу не имеет делителей нуля.
Идеал кольца, не совпадающий со всем кольцом и не содержащийся ни в каком большем идеале, не равном кольцу, называется максимальным. 20)
Гомоморфизм
Гомоморфизм колец (кольцевой гомоморфизм) — это отображение, сохраняющее операции сложения и умножения. А именно, гомоморфизм из кольца в кольцо — это функция такая что
Гомоморфизм колец называется изоморфизмом, если существует обратный гомоморфизм колец. Любой биективный гомоморфизм колец является изоморфизмом. Автоморфизм — это гомоморфизм из кольца в себя, который является изоморфизмом. Пример: тождественное отображение кольца на себя является автоморфизмом. 23)
Факторкольцо
Определение факторкольца по идеалу аналогично определению факторгруппы. Более точно, факторкольцо кольца по двустороннему идеалу — это множество классов смежности аддитивной группы по аддитивной подгруппе со следующими операциями:
Аналогично случаю групп, существует канонический гомоморфизм задаваемый как Ядром при этом является идеал
Аналогично теореме о гомоморфизме групп существует теорема о гомоморфизме колец: пусть тогда изоморфен факторкольцу по ядру гомоморфизма 26)
Некоторые особые классы колец
Примеры
Конструкции
Прямое произведение
Сходная конструкция существует для произведения произвольного семейства колец (сложение и умножение задаются покомпонентно). 43)
Пусть — коммутативное кольцо и — попарно взаимно простые идеалы в нём (идеалы называются взаимно простыми, если их сумма равна всему кольцу). Китайская теорема об остатках утверждает, что отображение
Кольцо эндоморфизмов
Поле частных и кольцо частных
Пусть R — целостное кольцо, тогда следующая конструкция позволяет построить наименьшее поле, содержащее его. Поле частных кольца R — это множество классов эквивалентности формальных дробей по следующему отношению эквивалентности:
тогда и только тогда, когда
с обычными операциями:
Не вполне очевидно, что заданное отношение действительно является отношением эквивалентности: для доказательства приходиться воспользоваться целостностью кольца. Существует обобщение данной конструкции на произвольные коммутативные кольца. А именно, пусть S — мультипликативно замкнутая система в коммутативном кольце R (то есть подмножество, содержащее единицу и не содержащее нуля; произведение любых двух элементов из подмножества снова ему принадлежит). Тогда кольцо частных — это множество классов эквивалентности формальных дробей по отношению эквивалентности:
Также эту конструкцию называют локализацией кольца (так как в алгебраической геометрии она позволяет исследовать локальные свойства многообразия в отдельной его точке). Пример: кольцо десятичных дробей — это локализация кольца целых чисел по мультипликативной системе
Категорное описание
Кольца вместе с гомоморфизмами колец образуют категорию, обычно обозначаемую Ring (иногда так обозначают категорию колец с единицей, а категорию обычных колец обозначают Rng). Категория колец с единицей обладает многими полезными свойствами: в частности, она полна и кополна. Это значит, что в ней существуют все малые пределы и копределы (например, произведения, копроизведения, ядра и коядра). Категория колец с единицей обладает начальным объектом (кольцо ) и терминальным объектом (нулевое кольцо).
Можно дать следующее категорное определение кольца: ассоциативное кольцо с единицей — это моноид в категории абелевых групп (абелевы группы образуют моноидальную категорию относительно операции тензорного произведения). Действие кольца R на абелевой группе (кольца, рассматриваемого как моноид по умножению) превращает абелеву группу в R-модуль. Понятие модуля обобщает понятие векторного пространства: грубо говоря, модуль — это «векторное пространство над кольцом». 48) 49)




