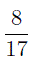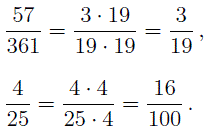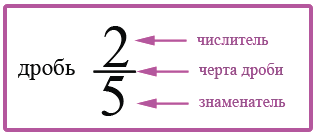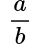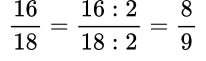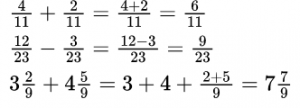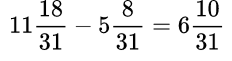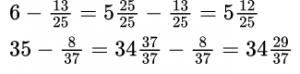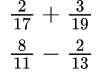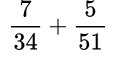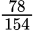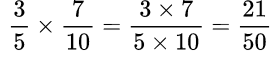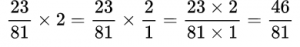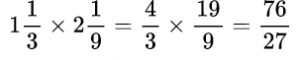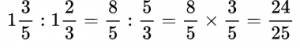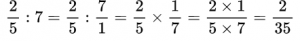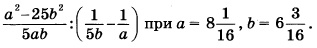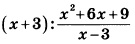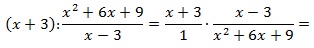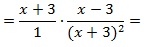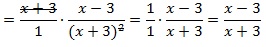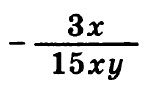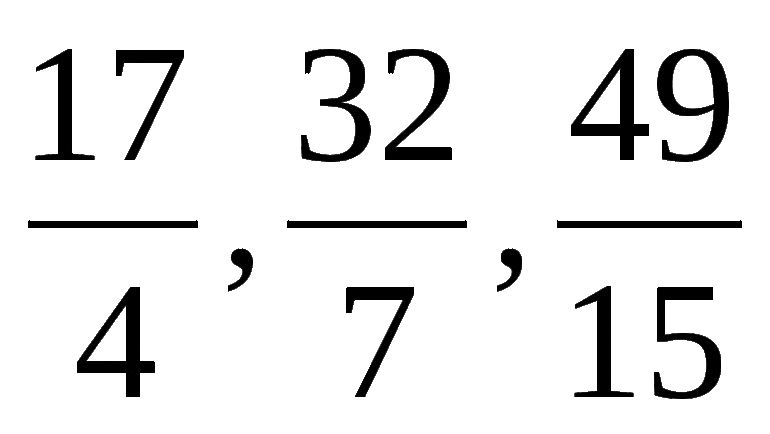что такое неравные дроби

Дробь. Правильные и неправильные дроби. Смешанные числа

Содержание

Дробь. Числитель и знаменатель дроби

Дробь записывают при помощи двух натуральных чисел, одно из которых стоит над горизонтальной чертой, а второе – под нею.

Знаменатель дроби показывает, на сколько одинаковых долей мы делим предмет или величину, а числитель дроби показывает, сколько таких долей взято.

Из рисунка 1 видно, что 24 километра составляют 4 из 7 частей маршрута. Таким образом, 1 часть маршрута равна

а весь маршрут равен

Термин дробь имеет синонимы: простая дробь, обыкновенная дробь, рациональная дробь, дробное число.

Правильные и неправильные дроби. Смешанные числа

– правильная дробь, и – неправильные дроби.

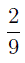
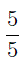
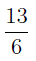
Неправильную дробь всегда можно представить в виде суммы целого числа и правильной дроби. Эту операцию называют выделением целой части из неправильной дроби и осуществляют при помощи деления с остатком числителя неправильной дроби на знаменатель.

Число 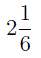является примером смешанного числа. Целое число 2 и правильную дробь называют целой и дробной частью смешанного числа соответственно.

Любое смешанное число всегда можно обратить в неправильную дробь, например,

Основное свойство дроби, сокращение дробей, несократимая дробь

Основным свойством дроби называют следующее

При помощи сокращений любую дробь можно превратить в равную ей несократимую дробь.

Источник

Доли. Обыкновенные дроби

Нам известно, что при подсчете чего-либо мы используем натуральные числа, но часто приходится что-то целое делить на части. Например, нам дан апельсин:

Допустим, нам надо разделить апельсин на 6 равных частей:

В этом случае каждую часть называют долей. То есть целый апельсин разделили на 6 частей, поэтому мы можем сказать, что апельсин это 1 целая, и 6 долей апельсина тоже составляет 1 целую:

Название долей зависит от числа частей. Каждая доля в нашем случае будет называться «одной шестой долей апельсина» или, короче, «одной шестой апельсина«. Если апельсин поделить на 8 частей, то мы получим восьмые доли. При этом, чем на большее число частей делят целое, тем меньше доля.

Например, рассмотрим брусок:

Разделим его на 5 частей:

То есть мы получим пятые доли бруска. Закрасим две части красным:

Теперь закрасим три части бруска:

Мы закрасили три пятые доли. Дробь, обозначающая эти доли, записывается так: .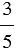

Теперь закрасим желтым цветом пять частей бруска:

Мы закрасили пять пятых долей, то есть мы закрасили весь брусок. Дробь, обозначающая эти доли, записывается так: .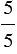

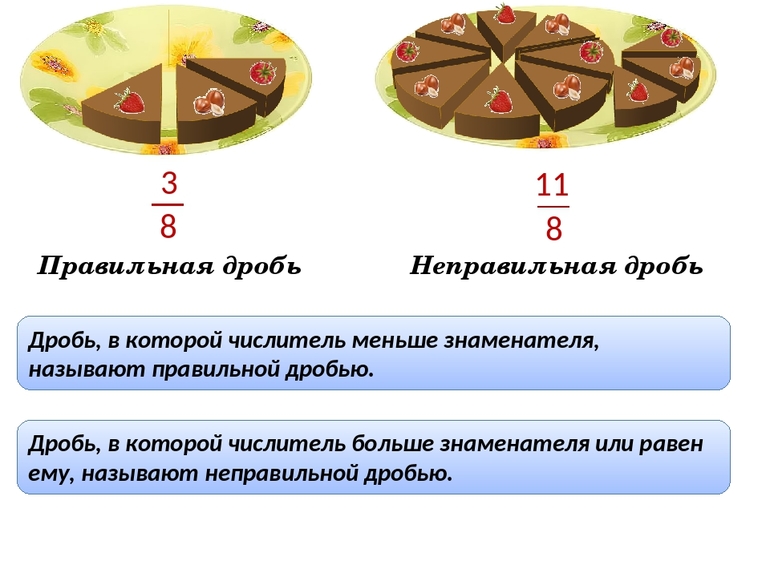
Рассмотрим рисунок ниже:

Определения

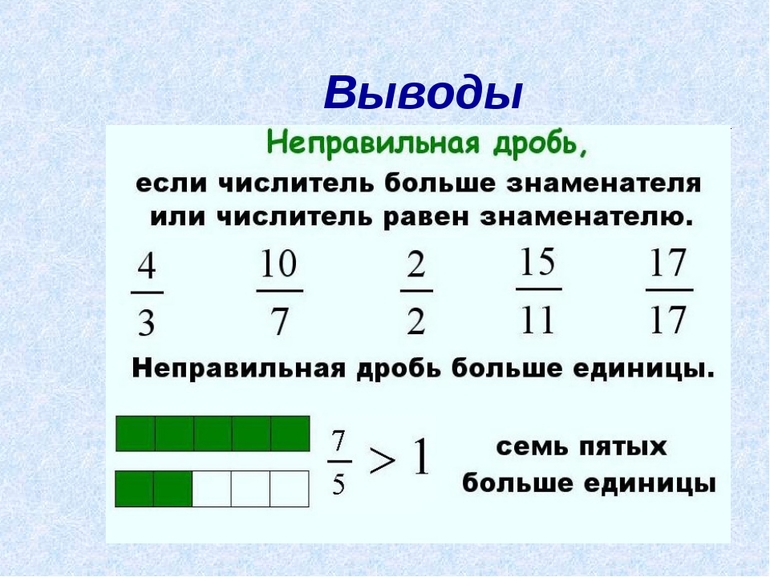
Правильная дробь – это дробь, числитель которой меньше знаменателя.

Неправильная дробь – это дробь, у которой числитель больше знаменателя или равен ему.

Поделись с друзьями в социальных сетях:

Источник

Обыкновенные дроби

теория по математике 📈 числа и вычисления

Обыкновенная дробь – это запись числа в виде:

где число a называют числителем, а число b – знаменателем дроби.

Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.

Пример №1. У первой дроби можно разделить числитель и знаменатель на одно и то же число 14, и получится равная ей дробь. Или как у второй дроби можно умножить числитель и знаменатель на одно и то же число, допустим, на 5.

Сократить дробь – значит разделить числитель и знаменатель на одно и то же число.

Пример №2. Чтобы сократить данную дробь надо вспомнить признаки делимости и увидеть, что числитель и знаменатель дроби — четные числа, значит, их можно разделить на 2, то есть дробь сокращается на 2:

Пример №3. По признаку делимости числитель и знаменатель делятся на 5, значит, сокращается данная дробь на 5.

Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями

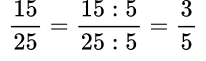
При сложении (вычитании) обыкновенных дробей с одинаковыми знаменателями нужно знаменатель оставить тем же, а числители сложить (вычесть). Если дроби смешанные, то отдельно складывают (вычитают) целые части.

Решения можно записывать короче, выполняя устно сложение или вычитание целых частей, а также – числителей.

Вычитание обыкновенной дроби из целого числа

Чтобы вычесть дробь из единицы, нужно единицу представить в виде неправильной дроби, числитель и знаменатель которой равны знаменателю вычитаемой дроби.

Пример №5. Представляем единицу в виде дроби и получаем вычитание дробей с одинаковыми знаменателями (числители можно вычесть устно).

Вычитание обыкновенной дроби из бóльшего числа

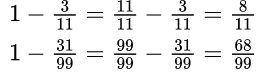
Чтобы вычесть обыкновенную дробь из числа, большего 1, необходимо представить эту дробь в виде смешанного числа, числитель и знаменатель которой равны также знаменателю вычитаемой дроби.

Сложение и вычитание дробей с разными знаменателями

Сложение и вычитание дробей с разными знаменателями требует предварительного приведения дробей к общему знаменателю. Существуют несколько приемов, которыми можно воспользоваться для нахождения общего знаменателя.

Нахождение общего знаменателя

Наименьшее общее кратное (НОК) – это наименьшее число, которое делится без остатка на данные знаменатели одновременно. Обычно его находят устно при выполнении действий с дробями.

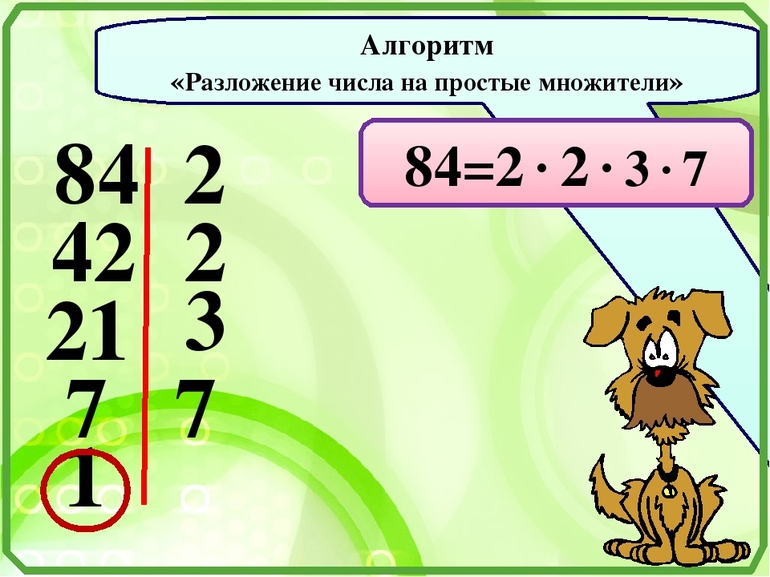
Правило нахождения НОК рассмотрим на примере чисел 12 и 15. Пример №7. 1. Нужно разложить на простые множители каждое число:

2. Затем найти одинаковые множители (подчеркиваем):

В данном случае это только множитель 3.

3. Взять одно из данных чисел и домножить на оставшиеся (не подчеркнутые) множители другого числа:

12 домножаем на 5: 12×5=60, или

15 домножаем на 2 и 2: 15×2×2=60

Таким образом, НОК =60. Обычно достаточно просто внимательно посмотреть на числа и в уме подобрать для них НОК.

Перемножение знаменателей. Приём №2.

Нам необходимо просто перемножить знаменатели. Обычно этот прием используется тогда, когда даны простые числа (которые делятся на 1 и на само себя) и на множители их не разложить.

Пример №8.

Для нахождения общего знаменателя в первом случае: 17×19=323, во втором: перемножаем 11 и 13, получаем 143.

Последовательный подбор. Приём №3.

Данный способ можно применить для небольших чисел устно: возьмем больший из знаменателей, умножим его на 2 и проверим, делится ли это число на второй знаменатель. Если нет, то умножим последовательно на 3, 4 и проверим аналогично.

Пример №9. Возьмем число 51, умножим на 2, получим 102 — видим, что 102 делится на 34, поэтому 102 и будет общий знаменатель.

После того, как мы научились находить общий знаменатель, приступаем непосредственно к алгоритму сложения (или вычитания) обыкновенных дробей с разными знаменателями.

Находим общий знаменатель. Можно использовать прием, когда умножаем 11 и 14, так как 11 — простое число. Следовательно, общий знаменатель равен 154. Находим дополнительный множитель к каждому числителю:

Выполняем умножение в числителе: Выполняем сложение дробей с одинаковыми знаменателями:

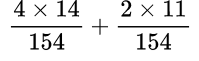
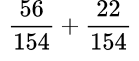
Умножение обыкновенных дробей

При умножении обыкновенных дробей получают дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.

При умножении обыкновенной дроби и целого числа необходимо целое число представить в виде дроби, числитель которой равен этому числу, а знаменатель равен 1 (что по сути означает перемножение числителя единственной первой дроби и целого числа, знаменатель же остается от первой дроби, так не меняется при умножении на единицу).

Если даны смешанные дроби, то необходимо сначала смешанную дробь перевести в неправильную, а затем выполнить умножение.

Пример №11. Здесь числитель 3 умножили на числитель 7, знаменатель 5 на знаменатель 10.

Пример №12. Случай, когда мы находим произведение дроби и целого числа. Целое число представили в виде дроби со знаменателем 1.

Пример №13. Нам даны смешанные дроби, переводим их в неправильные для выполнения умножения.

Деление обыкновенных дробей

При делении обыкновенных дробей необходимо делимое (то есть первую дробь) умножить на перевернутую вторую дробь, то есть дробь, обратную второй.

Если даны смешанные числа, то перед выполнением деления их необходимо перевести в обыкновенные неправильные дроби.

Если дробь нужно разделить на целое число, то его сначала нужно представить в виде дроби, а затем выполнить деление по правилу.

Пример №14. Делимое умножаем на число, обратное делителю. 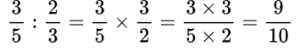Пример №15. Смешанные дроби сначала переводим в неправильные, а затем выполняем деление.

Пример №16. Деление дроби на целое число, где целое число 7 представлено в виде обыкновенной дроби.

Найдите значение выражения:

Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:

теперь переходим от деления дробей к их умножению:

затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:

сокращаем выражение на (a–5b): Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений): Подставим полученные значения в выражение и найдем конечный результат: Ответ: 39

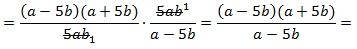
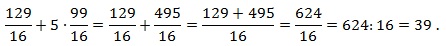
pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения при x = 12:

Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:

далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):

теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:

Подставляем числовое значение для х в полученное выражение и находим результат:

Ответ: 0,6

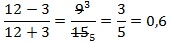
pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения

В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю — это b, для этого умножим первое слагаемое на b, после этого получим в числителе:

Приведем подобные слагаемые — это 9b² и — 9b², в числителе остается 5a. Запишем конечную дробь:

Вычислим её значение, подставив числа из условия:

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения:

Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель — это 15 x y, для этого необходимо первую дробь домножить на 5 y — и числитель и знаменатель, естественно:

Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:

5 y — (3 x + 5 y) = 5 y — 3 x — 5 y = — 3 x

Тогда дробь примет вид:

Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: — 1/5 y

Подставим значение y = 0,5: — 1 / (5 • 0,5) = — 1 / 2,5 = — 0,4

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения:

В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.

Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй — в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:

Далее выносим из числителя второй дроби a:

Подставляем значение a = 13:

pазбирался: Даниил Романович | обсудить разбор | оценить

Какое из данных ниже чисел является значением выражения?

Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?

Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.

После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:

Суммарно наши действия выглядят так:

pазбирался: Даниил Романович | обсудить разбор | оценить

Аналогично предыдущим заданиям вычисляем знаменатель: для этого приводим дроби к общему знаменателю — это 84. Для этого первую дробь умножаем на 4, а вторую на 3, получим:

1/21 + 1/28 = 4/84 + 3/84

Итак, мы получили в знаменателе 7/84, теперь делим числитель на знаменатель — это все равно что умножить 1 на обратную 7/84 дробь:

1 / ( 7 / 84 ) = 1 •84/7 = 84/7

Далее остается поделить 84 на 7:

pазбирался: Даниил Романович | обсудить разбор | оценить

Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что 1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17 • 1/3, поэтому её можно легко вынести за скобку.

Проведя вычисления в скобках, получим:

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник

Общие сведения

Слово «дробь» в обиход ввёл математик средневековой Европы Фибоначчи. На Руси под этим понятием понимались доли чисел. В дословном переводе на русский с арабского термин обозначает «ломать» или «раздроблять». Вид записи выражения, который применяется и сегодня, предложили арабы. Но фундамент теории заложили греческие и индийские учёные.

В математике под дробным отношением понимают число, образованное из некоторой части единицы. Простыми словами это можно объяснить на наглядном примере. Пусть на столе лежит две круглые пиццы. Каждую из них разрезали на восемь равных частей. Всего получилось шестнадцать долей. Через какое-то время было съедено одиннадцать кусков. Соответственно на столе осталось пять. В математической записи такое действие будет выглядеть как 11 / 8.

Число, стоящее в верхней части выражения, называют делимым или числителем, а в нижней делителем или знаменателем. В зависимости от их числового значения все дроби разделяют на три класса:

Кроме этого, выделяют ещё одну группу выражений. Дроби, относящиеся к ней, называют десятичными. Это такие отношения, у которых знаменатель — это десятичное число, стоящее в любой натуральной степени. Для записи десятичных выражений используют не дробную черту, а запятую. Например, 12 / 10 = 1,2.

Суть отношения

Обыкновенная дробь может быть правильной или неправильной. Например, 19 / 21 — правильное выражение, так как результат деления будет меньше единицы. В то же время обыкновенные числа 32 / 6 и 90 / 90 — неправильные, так как ответ, получаемый при делении, будет больше единицы в первом случае и равен ей во втором.

Чтобы разобраться, почему же дробные выражения, у которых числитель превосходит или равняется знаменателю называют «неправильными» можно порассуждать следующим образом.

Пусть имеется неправильная дробь 10 / 10. Эта запись обозначает, что взято десять долей чего-то состоящего из такого же числа частей. Иными словами, из имеющихся десяти долей можно сложить целый предмет. Неправильное выражение вида 10 / 10, по сути, означает целый предмет. Значит, можно записать, что 10 / 10 =1. Следовательно, такое отношение можно заменить натуральным числом.

Теперь можно рассмотреть неправильные отношения 7 / 3 и 12 / 4. Совершенно очевидно, что из этих семи третьих долей легко составляется два целых числа. Одно из них будет содержать три части. Значит, для оставшихся двух долей понадобится шесть частей: 3 + 3 = 6. При этом останется ещё одна доля — третья. Таким образом, выражение семь третьих означает две целые части и ещё одну третью от них. Аналогично из двенадцати четвёртых можно сформировать три целых числа по четыре доли в каждом. То есть дробное отношение 12 / 4 означает, по сути, три целых предмета.

Если провести анализ полученных результатов, то можно сделать вывод о том, что неправильные дроби, могут быть представлены в двух видах:

Особенный интерес вызывает представление неправильной дроби в виде суммы натурального числа и правильной части. Это действие называется выделением целой доли из неправильного отношения. Причём такая операция может быть выполнена и в обратном направлении — трансформация выражения в смешанное.

Превращение дробей

По смыслу неправильные выражения представляют собой целую и дробную часть, записанную в виде отношения. Поэтому любую смешанную дробь можно превратить в правильную, и наоборот. Деление целого числа на такое же можно объяснить так. Пусть нужно разделить четыре на пять. Значит, единицу понадобится разделить на пять равных частей, то есть 1 / 5. Четыре же единицы дадут 1 / 5 + 1/ 5 + 1 / 5 + 1 / 5 = 4 / 5. В этом случае получается правильное выражение. Но бывает, что числитель количественно превышает знаменатель. Значит, для более понятной формы записи нужно из такого выражения выделить целую часть.

Например, нужно преобразовать число 25 / 8. Это действие подразумевает нахождение целых единиц, содержащихся в выражении. Рассуждать нужно следующим образом. Одна единица может быть представлена как 8 / 8, две — 16 / 8, три — 24 / 8. Значит, число состоит из трёх единиц и оставшейся 1 / 8 части. Поэтому записать его можно так: 3 (1 / 8).

Такого вида преобразования часто приходится выполнять при решении примеров с дробями в 5 классе. Поэтому понять принцип превращения лучше всего на конкретное задание. При этом можно использовать следующий алгоритм:

Итак, пусть имеется выражение 3 (5 / 7). Так как фактически это сумма трёх и пяти седьмых, то следуя алгоритму, можно решение расписать так: 3 + 5 / 7 = (3 * 7 + 5) / 7 = (21 + 5) / 7 = 26 / 7. Аналогичный результат мог быть получен при простом сложении двух частей смешанного числа: 3 / 1 + 5 / 7 = (3 * 7) / 1 * 7 + 5 / 7 = 21 / 7 + 5 / 7 = (21 + 5) / 7 = 26 / 7. Первый вариант, конечно же, более удобен. Его можно выразить формулой: a (c / d) = (a * d + c) / d.

Эту выражение нужно обязательно запомнить, так как его придётся довольно часто использовать при решении задач различной сложности.

Выполнение действий

Отличие неправильной дроби от правильной заключается в том, что первая равна или больше единицы, а вторая меньше её. Поэтому правило выполнения арифметических действий одинаковое для этих двух групп. Для того чтобы ребёнок понял, как правильно решать простые и сложные задания объяснение в 5 классе неправильных дробей и действий над ними начинают с повторения правила разложения числа на простые множители.

Выполняется оно за несколько шагов. Вначале ищут минимальную величину, на которую можно разделить исходное без остатка. Далее, находят результат деления и повторяют действие, но уже для полученного числа. Операцию повторяют до тех пор, пока в ответе не получится единица.

Разложение на простые множители используется при поиске наименьшего знаменателя при сложении или вычитании неправильных дробей с разными делителями. Существует алгоритм, придерживаясь которого можно выполнить любое арифметическое действие над двумя и более дробными выражениями. Он заключается в следующем:

Например, 4 / 3 + 9 / 7 = (7 * 4) / 21 + (3 * 9) / 21 = 28 / 21 + 27 / 21 = (28 + 27) / 21 = 55 / 21 = 2 (13 / 21) и 56 / 9 — 6 / 9 = (56 — 6) / 9 = 50 / 9 = 5 (5 / 9).

Неправильные выражения можно не только складывать, но и вычитать. Для того чтобы их перемножить следует отдельно найти произведение делимых и делителей. Затем в числитель записать первый результат, а в знаменатель второй. То есть действие нужно выполнять по формуле: f / n * s / m = (f * s) / (n * m). Выполнить деление также просто. Для этого действия в вычитаемом выражении меняется местами аргументы и выполняется умножение: (f / n) / (s / m) = (f * m) / (n * s).

Источник