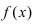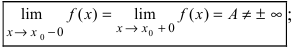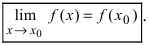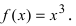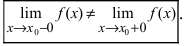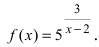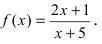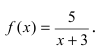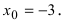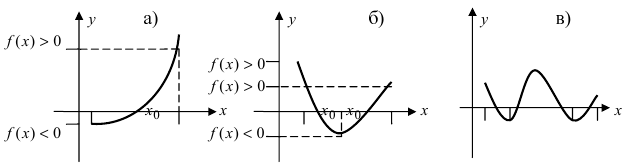что такое непрерывность в математике
Непрерывность (математика)
Исторически определенное для функций действительной переменной, понятие непрерывности обобщается на функции между метрическими пространствами или между топологическими пространствами в локальной форме и в глобальной форме.
Резюме
Определение реальных функций
Функция f называется непрерывной по a, если:
Комментарий
Примеры
Характеристики
Понятие непрерывности на интервале вещественных функций
Комбинация непрерывных функций является непрерывной функцией. Соединение непрерывной функции и сходящейся последовательности является сходящейся последовательностью.
Ошибки, которых следует избегать
Определение в случае метрических пространств
Определение
Мы говорим, что отображение f непрерывно в точке a, если:
Примеры
Общее определение (топологические пространства)
Местное определение
Мы можем сделать так, чтобы локальное определение (то есть точки) непрерывности опиралось на понятие предела :
Функция f называется непрерывной в точке a, если f ( a ) является пределом функции f в этой точке.
Глобальные характеристики
Мы можем вывести из локального определения три эквивалентные характеристики приложений, которые являются непрерывными (в любой точке исходного пространства).
Связь с интуитивным понятием заключается в следующем: когда функция «прыгает», это означает, что точки, очень близкие к исходному пространству, обнаруживаются на очень удаленных точках по прибытии. Однако для непрерывного приложения эти скачки невозможны, потому что, если мы рассмотрим начальную точку и ее изображение по прибытии, мы знаем, что вся окрестность этой начальной точки должна прибыть в окрестности точки прибытия. [не ясно]
Примеры
Эквивалентность метрического и топологического определения
Концепция преемственности в истории
Преемственность не всегда определялась прежним образом.
Эйлер в своем Introductio in analysin infinitorum определяет непрерывную функцию как функцию, определяемую одним конечным или бесконечным аналитическим выражением ( целым рядом ), и называет прерывными или смешанными функциями те, которые имеют несколько аналитических выражений в зависимости от интервалов. Сильвестр Лакруа (1810) называет непрерывной функцией функцию, все значения которой определяются одним и тем же законом или зависят от одного и того же уравнения. Это понятие непрерывности называется эйлеровой непрерывностью и является более строгим, чем нынешнее определение. Например, функция, определенная для любого отрицательного действительного числа как f ( x ) = x и любого положительного действительного числа как f ( x ) = x 2, является непрерывной в текущем смысле и смешанной (разрывной) в смысле Эйлера.
Непрерывность функций и точки разрыва с примерами решения
Содержание:
Непрерывность функций и точки разрыва
Непрерывность функции
Определение: Функция
— предел функции в точке 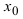
Пример:
Найти область непрерывности функции
Решение:
Данная функция непрерывна 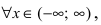
Замечание: Всякая элементарная функция непрерывна в области своего определения.
Точки разрыва
Определение: Точки, в которых не выполняется хотя бы одно из условий непрерывности функции, называются точками разрыва. Различают точки разрыва первого и второго родов.
Определение: Точкой разрыва I рода называется точка, в которой нарушается условие равенства лево- и правостороннего пределов, т.е.
Пример:
Доказать, что функция 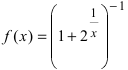
Решение:
Нарисуем график функции в окрестности нуля (Рис. 64): 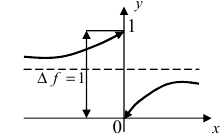
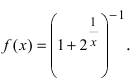
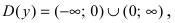
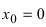
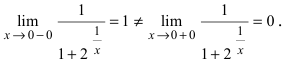
Замечание: По поводу точки разрыва I рода иначе говорят, что в этой точке функция испытывает конечный скачок (на Рис. 64 скачок равен 1).
Определение: Точка, подозрительная на разрыв, называется точкой устранимого разрыва, если в этой точке левосторонний предел равен правостороннему.
Пример:
Доказать, что функция 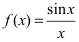
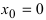
Решение:
В точке 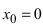
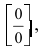
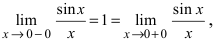
Определение: Все остальные точки разрыва называются точками разрыва II рода.
Замечание: Для точек разрыва второго рода характерен тот факт, что хотя бы
один из односторонних пределов равен 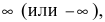
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 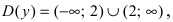
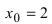
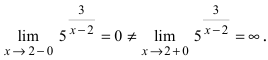
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 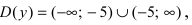
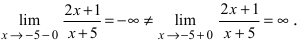
Операции над непрерывными функциями
Теорема: Сумма (разность) непрерывных функций есть непрерывная функция.
Доказательство: Докажем приведенную теорему для суммы двух функций 
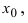
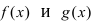
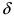
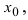
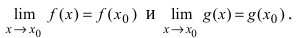
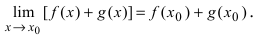
Теорема: Произведение непрерывных функций есть непрерывная функция.
Теорема: Частное двух непрерывных функций 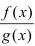
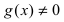
Теорема: Сложная функция от непрерывных функций есть непрерывная функция.
Схема исследования функции на непрерывность
Исследование функции на непрерывность проводят по следующей схеме:
Пример:
Исследовать на непрерывность функцию
Решение:
Согласно схеме исследования функции на непрерывность имеем:
Рис. 65. Поведение графика функции 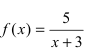
Из рисунка видно, что график функции 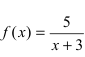
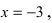
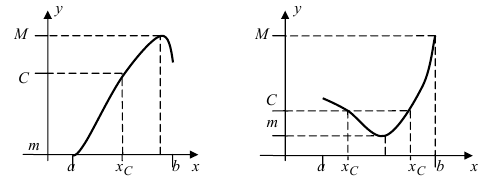
Свойства непрерывных функций на отрезке (a; b)
Свойства непрерывных функций на отрезке 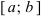
Определение: Замкнутый интервал 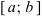
Приведем без доказательства свойства непрерывных функций на сегменте 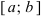
Теорема: Если функция 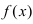
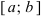
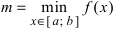
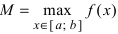
Пример:
Привести примеры графиков функций, удовлетворяющих условиям теорем(см. Рис. 66).
Рис. 66. Графики функций, удовлетворяющих условиям теоремы.
Решение:
На графике а) функция достигает своего наименьшего 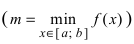
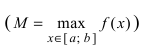
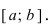
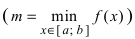
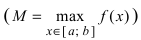
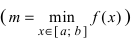
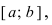
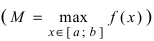
Тб. Если функция 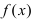
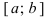
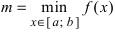
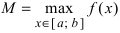
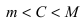
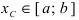
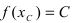
Пример:
Изобразить графики функций, удовлетворяющих условиям Тб (см. Рис. 67).
Рис. 67. Графики функций, удовлетворяющих условиям Тб.
Теорема: Если функция 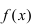
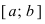
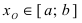
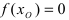
Пример:
Изобразить графики функций, удовлетворяющих условиям теоремы(см. Рис. 68).
Рис. 68. Графики функций, удовлетворяющих условиям теоремы.
На графике а) существует единственная точка, в которой выполняются условия теоремы. На графиках б) и в) таких точек две и четыре, соответственно. Однако в случаях б) и в) для удовлетворения условий теоремы надо разбивать сегмент на отдельные отрезки.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Непрерывность функции в точке, разрывы первого и второго рода
Процесс исследования функции на непрерывность неразрывно связан с навыком нахождения односторонних пределов функции. Поэтому, чтобы приступить к изучению материала данной статьи, желательно предварительно разобрать тему предела функции.
Непрерывность функции в точке
Данное определение позволяет вывести следствие: значение предела функции в точках непрерывности совпадает со значением функции в этих точках.
Решение
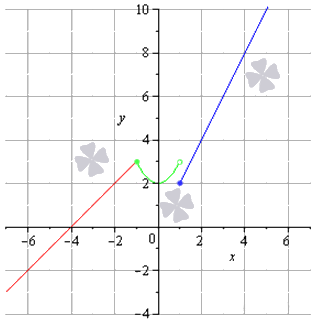
Соответствующая последовательность значений функций выглядит так:
на чертеже они обозначены зеленым цветом.
Соответствующая последовательность функций:
на рисунке обозначена синим цветом.
После вычисления значения функции в заданной точке очевидно выполнение равенства:
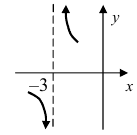
Устранимый разрыв первого рода
Решение
Ответ: пределы справа и слева являются равными, а заданная функция в точке х 0 = 5 не определена, т.е. в этой точке функция имеет устранимый разрыв первого рода.
Неустранимый разрыв первого рода
Неустранимый разрыв первого рода также определяется точкой скачка функции.
Решение
Определим пределы справа и слева от этих точек и значение заданной функции в этих точках:
Ответ: в конечном счете мы получили:
Нам остается только подготовить чертеж данного задания.
Разрыв второго рода (бесконечный разрыв)
Решение
Зададим произвольную последовательность значений аргумента, сходящуюся к х 0 слева. К примеру:
Ей соответствует последовательность значений функции:
CS108a. Непрерывная математика
Тематический план
Общее
Институт математики, механики и компьютерных наук им. И. И. Воровича
Направление «Фундаментальная информатика и информационные технологии»
Лектор к. ф.-м. н., доцент кафедры ИВЭ А.В. Абрамян
Лекция 1. Введение
Содержание лекции 1. Функция «модуль» и ее свойства. Функции «сигнум», «пол» и «потолок». Промежутки. Аксиома полноты. Ограниченные множества Свойства ограниченных множеств. Максимальный и минимальный элемент. Единственность максимального и минимального элемента. Верхняя и нижняя грань множества. Точная верхняя и точная нижняя грань множества.
Вводная лекция. Часть 1
Вводная лекция. Часть 2
Лекция 2. Предел последовательности
Содержание лекции 2. Определение последовательности. Предел последовательности Сходящиеся последовательности. Теорема о единственности предела последовательности. Теорема об ограниченности сходящейся последовательности. Теорема о пределе суммы, разности и произведения последовательностей. Следствие.
Лекция 3. Предел последовательности
Лекция 4. Предел последовательности
Содержание лекции 4. Бесконечно большие и бесконечно малые последовательности. Монотонные последовательности. Критерий сходимости возрастающей последовательности. Следствия. Приложения теоремы о пределе монотонной последовательности (шесть примеров). Число е.
Бесконечно большие и бесконечно малые последовательности. Монотонные последовательности. Критерий сходимости возрастающей последовательности. Следствия 1-3.
Следствие 4. Приложения теоремы о пределе монотонной последовательности (шесть примеров).
Лекция 5. Предел последовательности
Содержание лекции 5. Подпоследовательность. Теорема о пределе подпоследовательности. Частичный предел. Лемма Больцано-Вейерштрасса. Критерий Коши сходимости последовательности. Пример применения критерия Коши (расходимость гармонической последовательности)..
Подпоследовательность. Теорема о пределе подпоследовательности. Частичный предел. Лемма Больцано-Вейерштрасса.
Критерий Коши сходимости последовательности. Пример применения критерия Коши (расходимость гармонической последовательности).
Лекция 6. Предел функции
Ограниченные функции. Точная верхняя и точная нижняя грань функции. Максимум м минимум функции. Окрестность и выколотая окрестность точки. Свойства выколотых окрестностей.
Предел функции в точке. Теорема о единственности предела. Односторонний предел. Теорема о связи предела функции и односторонних пределов (критерий).
Лекция 7. Свойства пределов
Содержание лекции 7. Локальные свойства функции, имеющей предел. Арифметические операции с пределами.
Локальные свойства функции, имеющей предел. Арифметические операции с пределами: предел суммы и разности функций.
Арифметические операции с пределами: предел произведения и частного функций
Лекция 8. Свойства пределов
Содержание лекции 8. Свойства пределов, связанные с неравенствами. Монотонные функции. теорема об односторонних пределах монотонной функции на промежутке. Следствия. Первый замечательный предел. Второй замечательный предел. Бесконечно малые и бесконечно большие функции. Свойства бесконечно малых и бесконечно больших функций.
Три свойства пределов, связанные с неравенствами:
Определение монотонной и строго монотонной функции. Теорема о существовании односторонних пределов монотонной функции.
Три следствия к теореме о существовании односторонних пределов монотонной функции.
Лекция 9. Предел функции. Непрерывные функции
Содержание лекции 9.
Критерий Коши существования предела функции.Пример применения Критерия Коши.
Непрерывность
Полезное
Смотреть что такое «Непрерывность» в других словарях:
непрерывность — непрерывность … Орфографический словарь-справочник
Непрерывность — способность системы функционировать с заданными рабочими характеристиками в течение определенного периода. Примечание. Непрерывность характеризуется соответствующей вероятностью. Источник … Словарь-справочник терминов нормативно-технической документации
непрерывность — беспрерывность, непрестанность, беспрестанность, непрерывность; континуум, ежеминутность, постоянность, неизменность, неустанность, нескончаемость, сплошность, безустанность, перманентность, неумолчность, безостановочность, постоянство. Ant.… … Словарь синонимов
НЕПРЕРЫВНОСТЬ — неразрывная связь в бытии или переход в становлении. Всеобщность лейбницевского «закона непрерывности» (природа не делает скачков), согласно которому в природе нет никаких перерывов, пробелов и все связано благодаря переходам, была опровергнута… … Философская энциклопедия
непрерывность — Способность системы функционировать без перерывов в обслуживании с заданными рабочими характеристиками. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь справочник. Под редакцией Ю.М. Горностаева. Москва, 2002]… … Справочник технического переводчика
НЕПРЕРЫВНОСТЬ — НЕПРЕРЫВНОСТЬ, непрерывности, мн. нет, жен. отвлеч. сущ. к непрерывный. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
непрерывность — НЕПРЕРШЫВНЫЙ, ая, ое; вен, вна. Не имеющий перерывов, промежутков. Н. поток. Н. стаж работы. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
НЕПРЕРЫВНОСТЬ — (continuity) Отсутствие внезапных скачков функции. Функция у=f(x) является непрерывной, если при изменении значения х на сколь угодно малую величину не происходит внезапных изменений значения у. Некоторые функции непрерывны при всех значениях х,… … Экономический словарь
Непрерывность — [continuity] общее понятие математики и кибернетики, не имеющее, по видимому, общепринятого определения. В математике непрерывная функция та, значения которой близки, если близки значения аргументов. Для кибернетики здесь важно, что при… … Экономико-математический словарь
Непрерывность — (в рекламе) стратегия и тактика, используемые для составления графика рекламирования на все время рекламной кампании … Реклама и полиграфия
Непрерывность — В математике Непрерывная функция Непрерывное множество Непрерывное отображение Непрерывность (философия) Непрерывность (юридическая) действующий принцип, согласно которому судебное заседание по каждому делу происходит непрерывно, кроме времени,… … Википедия