что такое неориентированный граф
Основные определения теории графов
Содержание
Ориентированные графы [ править ]
| Определение: |
| Конечным графом (англ. finite graph) [math]G[/math] называется граф, в котором множества [math]V[/math] и [math]E[/math] — конечны. Следует заметить, что большинство рассматриваевых нами графов — конечны. |
| Определение: |
| Изоморфные графы (англ. isomorphic graphs) — два графа [math]A[/math] и [math]B[/math] называются изоморфными, если можно установить биекцию между их вершинами и соответствующими им рёбрами. |
Инцидентность (англ. incidence) — понятие, используемое только в отношении ребра и вершины. Две вершины или два ребра не могут быть инцидентны.
Заметим, что по определению ориентированного графа, данному выше, любые две вершины [math]u,
Данное определение разрешает соединять вершины более чем одним ребром. Такие рёбра называются кратными (иначе — параллельные, англ. multi-edge, parallel edge). Граф с кратными рёбрами принято называть мультиграфом (англ. multigraph). Если в мультиграфе присутствуют петли, то такой граф называют псевдографом (англ. pseudograph).
Неориентированный граф
В математической теории графов и информатике граф — это совокупность объектов со связями между ними.
Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.
Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные рёбра) — это связи, созданные гиперссылками (см. Тематическая карта).
Содержание
Определения
Теория графов не обладает устоявшейся терминологией. В различных статьях под одними и теми же терминами понимаются разные вещи. Приводимые ниже определения — наиболее часто встречаемые.
V (а значит и E ) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становятся ложными в случае бесконечных множеств.
Вершины и рёбра графа называются также элементами графа, число вершин в графе | V | — порядком, число рёбер | E | — размером графа.
Два ребра называются смежными, если они имеют общую концевую вершину.
Два ребра называются кратными, если множества их концевых вершин совпадают.
Степенью degV вершины V называют количество рёбер, для которых она является концевой (при этом петли считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
Ориентированный граф
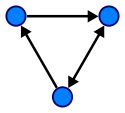
Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v 
Смешанный граф
Понятно, что ориентированный и неориентированный графы являются частными случаями смешанного.
Прочие связанные определения
Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Ориентированным путём в орграфе называют конечную последовательность вершин vi 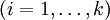
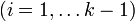
Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u,v,u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.
Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:
Бинарное отношение на множестве вершин графа, заданное как «существует путь из u в v », является отношением эквивалентности, и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.
Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа G. Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов
Ребро графа называется мостом, если его удаление увеличивает число компонент.
Дополнительные характеристики графов
Способы представления графа в информатике
Матрица смежности
Матрица смежности — таблица, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).
Недостатком являются требования к памяти — очевидно, квадрат количества вершин.
Матрица инцидентности
Данный способ является самым ёмким (размер пропорционален | E | | V | ) и неудобным для хранения, но облегчает нахождение циклов в графе.
Список рёбер
Список рёбер — это тип представления графа в памяти, подразумевающий, что каждое ребро представляется двумя числами — номерами вершин этого ребра. Список рёбер более удобен для реализации различных алгоритмов на графах по сравнению с матрицей смежности.
Обобщение понятия графа
Простой граф является одномерным симплициальным комплексом.
Более абстрактно, граф можно задать как тройку 


Под данное выше определение не подходят некоторые другие обобщения:
Литература
См. также
Ссылки
Популярные программы для визуализации графов
Что такое неориентированный граф
3.1 пТЙЕОФЙТПЧБООЩЕ Й ОЕПТЙЕОФЙТПЧБООЩЕ ЗТБЖЩ.
уРПУПВЩ ЪБДБОЙС ЗТБЖПЧ
V U E ПВТБЪХЕФ НОПЦЕУФЧП ЬМЕНЕОФПЧ ЗТБЖБ; РТЙ ЬФПН РТЕДРПМБЗБЕФУС, ЮФП е 
2. юБУФП ВЩЧБЕФ ЧБЦОП ПРТЕДЕМЙФШ, ЛБЛЙЕ ЗТБЖЩ УЮЙФБАФУС ТБЪМЙЮОЩНЙ, Б ЛБЛЙЕ ОЕ ТБЪМЙЮБАФУС. пВЩЮОП ЬФП УЧСЪЩЧБАФ У РПОСФЙЕН ЙЪПНПТЖЙЪНБ ЗТБЖПЧ. дЧБ ЗТБЖБ G1= (V1, E1, з1) Й G2= (V2, е2, з2) ОБЪЩЧБАФУС ЙЪПНПТЖОЩНЙ, ЕУМЙ УХЭЕУФЧХАФ ЧЪБЙНОП ПДОПЪОБЮОЩЕ ПФПВТБЦЕОЙС f: V1 V2 Й g: е1 е2, УПИТБОСАЭЙЕ ЙОГЙДЕОФОПУФШ, Ф.Е. ФБЛЙЕ, ЮФП ДМС ЧУСЛПЗП Е ™ е, ТБЧЕОУФЧП з1(e) = (v1,v2) ЧМЕЮЕФ ЪБ УПВПК ТБЧЕОУФЧП з2 (gЕ) = (fv1, fv2).
чП НОПЗЙИ УМХЮБСИ НПЦОП ТБУУНБФТЙЧБФШ ЗТБЖЩ У ФПЮОПУФША ДП ЙЪПНПТЖЙЪНБ, Ф.Е. ОЕ ТБЪМЙЮБФШ ЙЪПНПТЖОЩЕ ЗТБЖЩ; ПДОБЛП, ЕУМЙ ЛБЛЙЕ-ФП ЧЕТЫЙОЩ ЙМЙ ТЕВТБ ЗТБЖПЧ ПВМБДБАФ ТБЪМЙЮОПК ЙОДЙЧЙДХБМШОПУФША, ОБРТЙНЕТ, ПОЙ ЪБОХНЕТПЧБОЩ ЙМЙ ЙН УПРПУФБЧМЕОЩ ЛБЛЙЕ-МЙВП ЮЙУМЕООЩЕ ИБТБЛФЕТЙУФЙЛЙ (ЧЕУ ТЕВТБ, ДМЙОБ ТЕВТБ Й ДТ.), ФП ЕУФЕУФЧЕООП РТЙ УТБЧОЕОЙЙ ДЧХИ ЗТБЖПЧ ЬФХ ЙОДЙЧЙДХБМШОПУФШ ХЮЙФЩЧБФШ.
3. уХЭЕУФЧХЕФ ОЕУЛПМШЛП УРПУПВПЧ ЪБДБОЙС ЗТБЖПЧ, УЧСЪБООЩИ У ТБЪМЙЮОПК ЖПТНПК ЪБДБОЙС ЖХОЛГЙЙ з. чПФ ОЕЛПФПТЩЕ ЙЪ ОЙИ ДМС ЛПОЕЮОЩИ
1) рЕТЕЮЙУМЕОЙЕ (УРЙУПЛ) ТЕВЕТ ЗТБЖБ У ХЛБЪБОЙЕН ЙИ ЛПОГПЧ Й ДПВБЧМЕОЙЕН УРЙУЛБ ЙЪПМЙТПЧБООЩИ ЧЕТЫЙО.
еУМЙ НБФТЙГБ ЙОГЙДЕОГЙК ЪБДБЕФ ЗТБЖ ПДОПЪОБЮОП, ФП НБФТЙГБ УПУЕДУФЧБ ЧЕТЫЙО ПРТЕДЕМСЕФ ЗТБЖ У ФПЮОПУФША ДП ЪБНЕОЩ МАВПЗП ОЕПТЙЕОФЙТПЧБООПЗП ТЕВТБ РБТПК РТПФЙЧПРПМПЦОП ОБРТБЧМЕООЩИ ДХЗ НЕЦДХ ФЕНЙ ЦЕ ЧЕТЫЙОБНЙ. пДОБЛП ДМС ЗТБЖПЧ ВЕЪ ЛТБФОЩИ ТЕВЕТ ЪБДБОЙЕ ЗТБЖБ Й ЬФПК НБФТЙГЕК ПДОПЪОБЮОП, ЬМЕНЕОФЩ НБФТЙГЩ УПУЕДУФЧБ ТБЧОЩ Ч ЬФПН УМХЮБЕ 0 ЙМЙ 1.
нПЦОП РПЛБЪБФШ, ЮФП ЧУСЛЙК ЗТБЖ У ЛПОЕЮОЩН (Й ДБЦЕ УЮЕФОЩН) ЮЙУМПН ЬМЕНЕОФПЧ НПЦЕФ ВЩФШ ТЕБМЙЪПЧБО Ч ФТЕИНЕТОПН РТПУФТБОУФЧЕ, РТЙЮЕН, ЕУМЙ ЗТБЖ ОЕ УПДЕТЦЙФ ЛТБФОЩИ ТЕВЕТ, ФП ТЕВТБ НПЦОП ТЕБМЙЪПЧБФШ РТСНПМЙОЕКОЩНЙ ПФТЕЪЛБНЙ. оБ РМПУЛПУФЙ ТЕБМЙЪХЕФУС ОЕ ЧУСЛЙК ЗТБЖ, ЮФП РПТПЦДБЕФ ТБЪДЕМЕОЙЕ ЗТБЖПЧ ОБ РМПУЛЙЕ Й ОЕРМПУЛЙЕ. фЕН ОЕ НЕОЕЕ ДБЦЕ ОЕРМПУЛЙК ЗТБЖ ВЩЧБЕФ ХДПВОП ЙЪПВТБЦБФШ ОБ РМПУЛПУФЙ, ОБДП ФПМШЛП ПФМЙЮБФШ ЧЕТЫЙОЩ ПФ РЕТЕУЕЮЕОЙК ТЕВЕТ ОБ ТЙУХОЛЕ (ОБРТЙНЕТ, ЙЪПВТБЦБФШ ЧЕТЫЙОЩ ЛТХЦЛБНЙ); ПТЙЕОФБГЙА ТЕВЕТ РПЛБЪЩЧБАФ УФТЕМЛБНЙ.
еУМЙ РТЕДУФБЧЙФШ ЗТБЖПН ХМЙЮОХА (ДПТПЦОХА) УЕФШ, ЗДЕ ТЕВТБ ЙЪПВТБЦБАФ ПФТЕЪЛЙ ДПТПЗ, УЧСЪЩЧБАЭЙЕ УПУЕДОЙЕ ЧЕТЫЙОЩ (РМПЭБДЙ Й РЕТЕЛТЕУФЛЙ), ФП ДМС ОЕВПМШЫПЗП ОБУЕМЕООПЗП РХОЛФБ ФБЛПК ЗТБЖ НПЦЕФ ВЩФШ РМПУЛЙН, ОП ДМС ЗПТПДБ У РХФЕРТПЧПДБНЙ, НПУФБНЙ Й ФТБОУРПТФОЩНЙ ТБЪЧСЪЛБНЙ Ч ТБЪОЩИ ХТПЧОСИ, ПО УЛПТЕЕ ЧУЕЗП ОЕРМПУЛЙК.
| A= |  | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |  |
| -1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | -1 | 1 | 1 | -1 | -1 | 1 | 1 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | -1 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 2 |
| B= |  | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |  |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 1 | 0 | 2 | 0 | 0 | 0 | 0 | |||
| 0 | 1 | 2 | 0 | 3 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 2 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
4. тБУУНПФТЙН ОЕУЛПМШЛП РТЙНЕТПЧ ЗТБЖПЧ, ЙНЕАЭЙИ ЙОФЕТЕУОЩЕ РТЙНЕОЕОЙС.
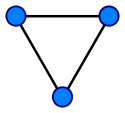
оБ ТЙУХОЛЕ 2 Б, В, Ч ЙЪПВТБЦЕОЩ ЗТБЖЩ л3, л4, л5. оБ ТЙУХОЛЕ 2 З ЗТБЖ л5 РТЕДУФБЧМЕО У НЙОЙНБМШОЩН ЮЙУМПН РЕТЕУЕЮЕОЙК ЙЪПВТБЦЕОЙК ТЕВЕТ: ХУФТБОЙФШ ЙИ РПМОПУФША ОЕМШЪС.
 |  |  |  |
| a | В | Ч | З |
| тЙУХОПЛ 2 | |||
(3) n-НЕТОЩН ЕДЙОЙЮОЩН ЛХВПН ОБЪЩЧБЕФУС ЗТБЖ еn, ЧЕТЫЙОБНЙ ЛПФПТПЗП СЧМСАФУС ЧУЕ ОБВПТЩ ДМЙОЩ n ЙЪ ОХМЕК Й ЕДЙОЙГ, Б ТЕВТБ УПЕДЙОСАФ ЧЕТЫЙОЩ, ТБЪМЙЮБАЭЙЕУС ТПЧОП Ч ПДОПК ЛПНРПОЕОФЕ. уМХЮБЙ n = 3 Й n = 4 РТЕДУФБЧМЕОЩ ОБ ТЙУХОЛЕ 4 Б, В.
 |  |
| a | В |
| тЙУХОПЛ 4 | |
хРТБЦОЕОЙЕ. дПЛБЦЙФЕ, ЮФП ЗТБЖЩ еn СЧМСАФУС ДЧХДПМШОЩНЙ (ХЛБЪБОЙЕ: ТБУУНПФТЙФЕ ОБВПТЩ У ТБЪМЙЮОЩН ЮЙУМПН ЕДЙОЙГ).
5. зТБЖ о = (V’, е’) ОБЪЩЧБЕФУС РПДЗТБЖПН ЗТБЖБ G = (V, е), ПВПЪОБЮЕОЙЕ: о G, ЕУМЙ V’ V, е’ е Й ДМС НОПЦЕУФЧ V’ Й е’ УПИТБОСАФУС ЙОГЙДЕОГЙЙ ЗТБЖБ G. рТЙ ЬФПН, ПЮЕЧЙДОП, ЛБЦДПЕ ТЕВТП ЙЪ е’ ЧИПДЙФ Ч РПДЗТБЖ о ЧНЕУФЕ УП УЧПЙНЙ ЛПОГБНЙ.
йОПЗДБ ТБУУНБФТЙЧБАФУС ФПМШЛП РПДЗТБЖЩ ВЕЪ ЙЪПМЙТПЧБООЩИ ЧЕТЫЙО ЙМЙ ФПМШЛП РПДЗТБЖЩ, УПДЕТЦБЭЙЕ ЧУЕ ЧЕТЫЙОЩ ЗТБЖБ (Й ФПМШЛП ЮБУФШ ТЕВЕТ); ФБЛЙЕ РПДЗТБЖЩ РПМОПУФША ПРТЕДЕМСАФУС НОПЦЕУФЧПН УЧПЙИ ТЕВЕТ. ч ЬФЙИ УМХЮБСИ НПЦОП ЕУФЕУФЧЕООЩН ПВТБЪПН ПРТЕДЕМЙФШ ФЕПТЕФЙЛП-НОПЦЕУФЧЕООЩЕ ПРЕТБГЙЙ ОБД РПДЗТБЖБНЙ: РЕТЕУЕЮЕОЙЕ, ПВЯЕДЙОЕОЙЕ, УЙННЕФТЙЮЕУЛХА ТБЪОПУФШ (ОБЪЩЧБЕНХА ФБЛЦЕ УХННПК РП НПДХМА 2 ЙМЙ РТПУФП УХННПК), ДПРПМОЕОЙЕ ДП ЧУЕЗП ЗТБЖБ. рПДЗТБЖПН, ОБФСОХФЩН ОБ НОПЦЕУФЧП ЧЕТЫЙО V’ V ЗТБЖБ G, ОБЪЩЧБЕФУС РПДЗТБЖ, УПДЕТЦБЭЙК ЧЕТЫЙОЩ ЙЪ V Й ЧУЕ ТЕВТБ ЗТБЖБ G, УПЕДЙОСАЭЙЕ РБТЩ ЧЕТЫЙО ЙЪ V’.
рПДЗТБЖ Z 




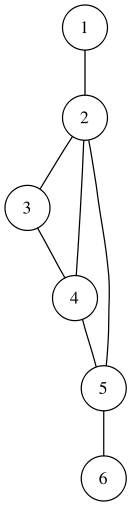
дМС ЗТБЖБ, ЙЪПВТБЦЕООПЗП ОБ ТЙУХОЛЕ 1, s(v1) = 1, s(v2) = s(v3) = 3, s(v4)= 7,s(v6) = 0.
еУМЙ ЧУЕ ЧЕТЫЙОЩ ЗТБЖБ ЙНЕАФ ПДЙОБЛПЧХА УФЕРЕОШ s (ФБЛПК ЗТБЖ ОБЪЩЧБАФ ПДОПТПДОЩН), ФП УХННБ УФЕРЕОЕК ЕЗП ЧЕТЫЙО ТБЧОБ b • s, Б ЮЙУМП ТЕВЕТ ТБЧОП b • s / 2.
хРТБЦОЕОЙЕ. пРТЕДЕМЙФЕ ЮЙУМП ТЕВЕТ Ч ЗТБЖБИ е3, е4 (ТЙУХОПЛ 4Б, В).
ч ОЕПТЙЕОФЙТПЧБООПН ЗТБЖЕ УХННБ УФЕРЕОЕК ЧУЕИ ЧЕТЫЙО ТБЧОБ ХДЧПЕООПНХ ЮЙУМХ ТЕВЕТ m ЗТБЖБ, Ф.Е. ЮЕФОБ.
рЕФМС ДБЕФ ЧЛМБД 2 Ч УФЕРЕОШ ЧЕТЫЙОЩ.
пФУАДБ УМЕДХЕФ, ЮФП Ч ОЕПТЙЕОФЙТПЧБООПН ЗТБЖЕ ЮЙУМП ЧЕТЫЙО ОЕЮЕФОПК УФЕРЕОЙ ЮЕФОП.
рЕФМС ДБЕФ ЧЛМБД 1 Ч ПВЕ ЬФЙ УФЕРЕОЙ.
ч ПТЗТБЖЕ УХННЩ УФЕРЕОЕК ЧУЕИ ЧЕТЫЙО ρ1(ν) Й ρ2(ν) ТБЧОЩ ЛПМЙЮЕУФЧХ ТЕВЕТ m ЬФПЗП ЗТБЖБ, Б ЪОБЮЙФ, Й ТБЧОЩ НЕЦДХ УПВПК.
еУМЙ УФЕРЕОШ ЧЕТЫЙОЩ ТБЧОБ 0, Ф.Е. d(ν)=0, ФП ЧЕТЫЙОБ ОБЪЩЧБЕФУС ЙЪПМЙТПЧБООПК. еУМЙ УФЕРЕОШ ЧЕТЫЙОЩ ТБЧОБ 1, d(ν)=1, ФП ЧЕТЫЙОБ ОБЪЩЧБЕФУС ЛПОГЕЧПК ЙМЙ ЧЙУСЮЕК.
уХННБ УФЕРЕОЕК ЧЕТЫЙО ЗТБЖБ ТБЧОБ ХДЧПЕООПНХ ЛПМЙЮЕУФЧХ ТЕВЕТ.
нОПЦЕУФЧП ЧЕТЫЙО ЗТБЖБ ОБЪЩЧБЕФУС ОЕЪБЧЙУЙНЩН (ЧОХФТЕООЕ ХУФПКЮЙЧЩН), ЕУМЙ ОЙЛБЛЙЕ ДЧЕ ЧЕТЫЙОЩ ЙЪ ЬФПЗП НОПЦЕУФЧБ ОЕ УНЕЦОЩ. оЕЪБЧЙУЙНПЕ НОПЦЕУФЧП ЧЕТЫЙО ОБЪЩЧБЕФУС НБЛУЙНБМШОЩН, ЕУМЙ ПОП ОЕ СЧМСЕФУС УПВУФЧЕООЩН РПДНОПЦЕУФЧПН ОЕЛПФПТПЗП ДТХЗПЗП ОЕЪБЧЙУЙНПЗП НОПЦЕУФЧБ. оБЙВПМШЫЕЕ РП НПЭОПУФЙ ЙЪ НБЛУЙНБМШОЩИ ОЕЪБЧЙУЙНЩИ НОПЦЕУФЧ ОБЪЩЧБЕФУС ОБЙВПМШЫЙН. юЙУМП ЧЕТЫЙО Ч ОБЙВПМШЫЕН ОЕЪБЧЙУЙНПН НОПЦЕУФЧЕ ЗТБЖБ G ОБЪЩЧБЕФУС ЮЙУМПН ОЕЪБЧЙУЙНПУФЙ (ЮЙУМПН ЧОХФТЕООЕК ХУФПКЮЙЧПУФЙ, ОЕРМПФОПУФША) Й ПВПЪОБЮБЕФУС ЮЕТЕЪ α0(G).
оБ ТЙУХОЛЕ 5 РПЛБЪБО ЗТБЖ G, Х ЛПФПТПЗП ЮЙУМП ОЕЪБЧЙУЙНПУФЙ α0(G)=4. нОПЦЕУФЧП ЧЕТЫЙО <ν1,ν2,ν3,ν7>; <ν1,ν2,ν3,ν8>; <ν2,ν3,ν5,ν7>; <ν2,ν3,ν5,ν8> СЧМСАФУС ОБЙВПМШЫЙНЙ ОЕЪБЧЙУЙНЩНЙ НОПЦЕУФЧБНЙ. нОПЦЕУФЧП ЧЕТЫЙО <ν4,ν7> СЧМСЕФУС НБЛУЙНБМШОЩН ОЕЪБЧЙУЙНЩН НОПЦЕУФЧПН, ОП ОЕ ОБЙВПМШЫЙН.
оЕЪБЧЙУЙНЩЕ НОПЦЕУФЧБ ТЕВЕТ ЗТБЖБ G ОБИПДСФУС ЧП ЧЪБЙНОП ПДОПЪОБЮОПН УППФЧЕФУФЧЙЙ У ОЕЪБЧЙУЙНЩН НОПЦЕУФЧПН ЧЕТЫЙО ТЕВЕТОПЗП ЗТБЖБ L(G), Ф.Е. α1(G)=α0((L)G)).
Граф (теория графов)
В математической теории графов и информатике граф — это совокупность объектов со связями между ними.
Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.
Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные рёбра) — это связи, созданные гиперссылками (см. Тематическая карта).
Содержание
Определения
Теория графов не обладает устоявшейся терминологией. В различных статьях под одними и теми же терминами понимаются разные вещи. Приводимые ниже определения — наиболее часто встречаемые.
V (а значит и E ) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становятся ложными в случае бесконечных множеств.
Вершины и рёбра графа называются также элементами графа, число вершин в графе | V | — порядком, число рёбер | E | — размером графа.
Два ребра называются смежными, если они имеют общую концевую вершину.
Два ребра называются кратными, если множества их концевых вершин совпадают.
Степенью degV вершины V называют количество рёбер, для которых она является концевой (при этом петли считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
Ориентированный граф
Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v 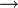
Смешанный граф
Понятно, что ориентированный и неориентированный графы являются частными случаями смешанного.
Прочие связанные определения
Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Ориентированным путём в орграфе называют конечную последовательность вершин vi 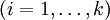
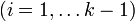
Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u,v,u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.
Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:
Бинарное отношение на множестве вершин графа, заданное как «существует путь из u в v », является отношением эквивалентности, и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.
Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа G. Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов
Ребро графа называется мостом, если его удаление увеличивает число компонент.
Дополнительные характеристики графов
Способы представления графа в информатике
Матрица смежности
Матрица смежности — таблица, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).
Недостатком являются требования к памяти — очевидно, квадрат количества вершин.
Матрица инцидентности
Данный способ является самым ёмким (размер пропорционален | E | | V | ) и неудобным для хранения, но облегчает нахождение циклов в графе.
Список рёбер
Список рёбер — это тип представления графа в памяти, подразумевающий, что каждое ребро представляется двумя числами — номерами вершин этого ребра. Список рёбер более удобен для реализации различных алгоритмов на графах по сравнению с матрицей смежности.
Обобщение понятия графа
Простой граф является одномерным симплициальным комплексом.
Более абстрактно, граф можно задать как тройку 


Под данное выше определение не подходят некоторые другие обобщения:
Литература
См. также
Ссылки
Популярные программы для визуализации графов