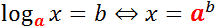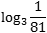что такое натуральный логарифм простыми словами
Что такое логарифм
Логарифмы всегда считались сложной темой в школьном курсе математики. Существует много разных определений логарифма, но большинство учебников почему-то используют самые сложные и неудачные из них.
Мы же определим логарифм просто и наглядно. Для этого составим таблицу:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.
А теперь — собственно, определение логарифма:
Например, 2 3 = 8 ⇒ log2 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2 3 = 8). С тем же успехом log2 64 = 6, поскольку 2 6 = 64.
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log2 2 = 1 | log2 4 = 2 | log2 8 = 3 | log2 16 = 4 | log2 32 = 5 | log2 64 = 6 |
Если взять калькулятор и посчитать, чему равны такие логарифмы, то получатся очень длинные числа. Взгляните сами:
log2 5 = 2,32192809.
log3 8 = 1,89278926.
log5 100 = 2,86135311.
Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log2 5, log3 8, log5 100.
Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:
Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.
Как считать логарифмы
С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:
Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0, a > 0, a ≠ 1.
Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:
Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.
Посмотрим, как работает эта схема на конкретных примерах:
Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. И если такие множители нельзя собрать в степени с одинаковыми показателями, то и исходное число не является точной степенью.
Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14.
8 = 2 · 2 · 2 = 2 3 — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;
Заметим также, что сами простые числа всегда являются точными степенями самих себя.
Десятичный логарифм
Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.
Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.
Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x = log10 x
Все, что верно для обычных логарифмов, верно и для десятичных.
Натуральный логарифм
Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.
Не будем углубляться, что это за число и зачем нужно. Просто помните, что e — основание натурального логарифма:
ln x = log e x
Таким образом, ln e = 1; ln e 2 = 2; ln e 16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.
Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.
Логарифм. Натуральный логарифм.
За основание логарифмов нередко берут цифру е = 2,718281828. Логарифмы по данному основанию именуют натуральным. При проведении вычислений с натуральными логарифмами общепринято оперировать знаком ln, а не log; при этом число 2,718281828, определяющие основание, не указывают.
Само число е определяет предел монотонной ограниченной последовательности
Весьма часто для фиксации в памяти какого либо числа, цифры необходимого числа ассоциируют с какой-нибудь выдающейся датой. Скорость запоминания первых девяти знаков числа е после запятой возрастет, если заметить, что 1828 — это год рождения Льва Толстого!
На сегодняшний день существуют достаточно полные таблицы натуральных логарифмов.
График натурального логарифма (функции y = ln x) является следствием графика экспоненты зеркальным отражением относительно прямой у = х и имеет вид:
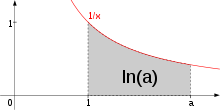
Натуральный логарифм может быть найден для каждого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a.
Элементарность этой формулировку, которая состыковывается со многими другими формулами, в которых задействован натуральный логарифм, явилось причиной образования названия «натуральный».
Если анализировать натуральный логарифм, как вещественную функцию действительной переменной, то она выступает обратной функцией к экспоненциальной функции, что сводится к тождествам:
По аналогии со всеми логарифмами, натуральный логарифм преобразует умножение в сложение, деление в вычитание:
Логарифм может быть найден для каждого положительного основания, которое не равно единице, а не только для e, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, обычно, определяются в терминах натурального логарифма.
Проанализировав график натурального логарифма, получаем, что он существует при положительных значениях переменной x. Он монотонно возрастает на своей области определения.
При x →0 пределом натурального логарифма выступает минус бесконечность ( –∞ ).При x → +∞ пределом натурального логарифма выступает плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a возрастает быстрее логарифма. Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумы у него отсутствуют.
Использование натуральных логарифмов весьма рационально при прохождении высшей математики. Так, использование логарифма удобно для нахождения ответа уравнений, в которых неизвестные фигурируют в качестве показателя степени. Применение в расчетах натуральных логарифмом дает возможность изрядно облегчить большое количество математических формул. Логарифмы по основанию е присутствуют при решении значительного числа физических задач и естественным образом входят в математическое описание отдельных химических, биологических и прочих процессов. Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.
Натуральный логарифм
Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа, о чём будет сказано ниже.
Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:

Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:
Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции:
Логарифм может быть определён для любого положительного основания, отличного от 1, а не только для e, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, как правило, определяются в терминах натурального логарифма. Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности. Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
Содержание
История
Конвенции об обозначениях
Русская (и советская в целом) система
Натуральный логарифм принято обозначать через «ln(x)», логарифм по основанию 10 — через «lg(x)», а прочие основания принято указывать явно при символе «log».
Во многих работах по дискретной математике, кибернетике, информатике авторы используют обозначение «log(x)» для логарифмов по основанию 2, но это соглашение не является общепринятым и требует разъяснения либо в списке использованных обозначений, либо (при отсутствии такого списка) сноской или комментарием при первом использовании.
Англо-американская система
Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(x)» (или изредка «loge(x)»), когда они имеют в виду натуральный логарифм, а запись «log(x)» у них означает log10(x).
В теоретической информатике, теории информации и криптографии «log(x)» обычно означает логарифм по основанию 2 «log2(x)» (хотя часто вместо этого пишется просто lg(x)).
Техника
В наиболее часто используемых языках программирования и пакетах прикладных программ, включая C, C++, SAS, MATLAB, Фортран и BASIC функция «log» или «LOG» относится к натуральному логарифму.
В ручных калькуляторах натуральный логарифм обозначается ln, тогда как log служит для обозначения логарифма по основанию 10.
Происхождение термина натуральный логарифм
Сначала может показаться, что поскольку наша система счисления имеет основание 10, то это основание является более «натуральным», чем основание e. Но математически число 10 не является особо значимым. Его использование скорее связано с культурой, оно является общим для многих систем счисления, и связано это, вероятно, с числом пальцев у людей. [5] Некоторые культуры основывали свои системы счисления на других основаниях: 5, 8, 12, 20 и 60. [6] [7] [8]
loge является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции: [9]
Если основание b равно e, то производная равна просто 1/x, а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора, чего нельзя сказать о других логарифмах.
Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николай Меркатор называли их логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление. [10]
Определение
Формально ln(a) может быть определён как площадь под кривой графика 1/x от 1 до a, т. е. как интеграл:
Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:
Это можно продемонстрировать, допуская 
Число e может быть определено как единственное действительное число a такое, что ln(a) = 1.
Или же, если показательная функция была определена раньше с использованием бесконечных рядов, натуральный логарифм может быть определён как обратная к ней функция, т. е. ln — это функция, такая что 
Свойства
Производная, ряд Тейлора
Производная натурального логарифма равна
На основании этого можно выполнить разложение 

С помощью преобразования Эйлера ряда Меркатор можно получить следующее выражение, которое справедливо для любого х больше 1 по абсолютной величине:
Этот ряд похож на формулу Бэйли—Боруэйна—Плаффа.
Также заметим, что 

Натуральный логарифм в интегрировании
Натуральный логарифм даёт простую интегральную функцию вида g(x) = f ‘(x)/f(x): первообразная функции g(x) имеет вид ln(|f(x)|). Это подтверждается цепным правилом и следующим фактом:
Ниже дан пример для g(x) = tan(x):


где C — произвольная константа.
Натуральный логарифм можно проинтегрировать с помощью интегрирования по частям:
Численное значение
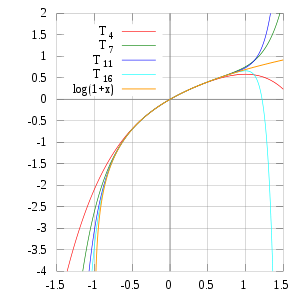
Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:
Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:
 |  |
 |
при условии, что y = (x−1)/(x+1) и x > 0.
Для ln(x), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:
 |  |
 | |
 | |
 |
Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.
Высокая точность
Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона, чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой для очень высокой точности расчёта является формула: [12] [13]
где M обозначает арифметико-геометрическое среднее 1 и 4/s, и

,» border=»0″ />
m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)
Вычислительная сложность
Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M(n) ln n). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M(n) — вычислительная сложность умножения двух n-значных чисел.
Непрерывные дроби
Хотя для представления логарифма отсутствуют простые непрерывные дроби, но можно использовать несколько обобщённых непрерывных дробей, в том числе:

Комплексные логарифмы
Логарифм не может быть определён на всей комплексной плоскости, и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi. Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi, и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi, или 10πi или −6 πi, и так далее.
Логарифмы и их свойства
Обычно определение логарифма дают очень сложно и запутанно. Мы постараемся сделать это очень просто и наглядно.
Для того, чтобы разобраться, что такое логарифм, давайте рассмотрим пример:
Все знакомы, что такое степень числа (если нет, то вам сюда). В таблице приведены различные степени числа 2. Глядя на таблицу, ясно, что, например, число 32 – это 2 в пятой степени, то есть двойка, умноженная на саму себя пять раз.
Теперь при помощи этой таблицы введем понятие логарифма.
Логарифм от числа 32 по основанию 2 (\(log_<2>(32)\)) – это в какую степень нужно возвести двойку, чтобы получить 32. Из таблицы видно, что 2 нужно возвести в пятую степень. Значит наш логарифм равен 5:
Аналогично, глядя в таблицу получим, что:
Естественно, логарифм бывает не только по основанию 2, а по любым основаниям больших 0 и неравных 1. Можете так же создавать таблицы для разных чисел. Но, конечно, со временем вы это будете делать в уме.
Теперь дадим определение логарифма в общем виде:
Логарифмом положительного числа \(b\) по основанию положительно числа \(a\) называется степень \(c\), в которую нужно возвести число \(a\), чтобы получить \(b\)
Но, конечно, вы часто будете сталкиваться не с такими простыми логарифмами, как в примерах с двойкой, а очень часто будет, что логарифм нельзя в уме посчитать. Действительно, что скажете про логарифм пяти по основанию два:
Как его посчитать? При помощи калькулятора. Он нам покажет, что такой логарифм равен иррациональному числу:
Или логарифм шести по основанию 4:
На уроках математики пользоваться калькулятором нельзя, поэтому на экзаменах и контрольных принято оставлять такие логарифмы в виде логарифма – не считая его, это не будет ошибкой!
Но иногда можно столкнуться с заданием, где нужно примерно оценить значение логарифма – это очень просто! Давайте для примера оценим логарифм \(log_<4>(6)\). Необходимо подобрать слева и справа от 6 такие ближайшие числа, логарифм от которых мы сможем посчитать, другими словами, надо найти степени 4-ки ближайшие к 6ке:
Значит \(log_<4>(6)\) принадлежите промежутку от 1 до 2:
Как посчитать логарифм
Почему так? Это следует из определения показательной функций. Показательная функция не может быть \(0\). А основание не равно \(1\), потому что тогда логарифм теряет смысл – ведь \(1\) в любой степени это будет \(1\).
При этих ограничениях логарифм существует.
В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.
Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д.
Теперь давайте разберем общий алгоритм вычисления логарифмов:
Давайте разберем на примерах.
Пример 1. Посчитать логарифм \(9\) по основанию \(3\): \(log_<3>(9)\)
Пример 2. Вычислить логарифм \(\frac<1><125>\) по основанию \(5\): \(log_<5>(\frac<1><125>)\)
Пример 3. Вычислить логарифм \(4\) по основанию \(64\): \(log_<64>(4)\)
Пример 4. Вычислить логарифм \(1\) по основанию \(8\): \(log_<8>(1)\)
Пример 5. Вычислить логарифм \(15\) по основанию \(5\): \(log_<5>(15)\)
Как понять, что некоторое число \(a\) не будет являться степенью другого числа \(b\). Это довольно просто – нужно разложить \(a\) на простые множители.
\(16\) разложили, как произведение четырех двоек, значит \(16\) будет степенью двойки.
Разложив \(48\) на простые множители, видно, что у нас есть два множителя \(2\) и \(3\), значит \(48\) не будет степенью.
Теперь поговорим о наиболее часто встречающихся логарифмах. Для них даже придумали специально названия – десятичный логарифм и натуральный логарифм. Давайте разбираться.
Десятичный логарифм
Натуральный логарифм
Натуральные и десятичные логарифмы подчиняются тем же самым свойствам и правилам, что и обыкновенные логарифмы.
У логарифмов есть несколько свойств, по которым можно проводить преобразования и вычисления. Кроме этих свойств, никаких операций с логарифмами делать нельзя.
Свойства логарифмов
Давайте разберем несколько примеров на свойства логарифмов.
Пример 8. Воспользоваться формулой \(3\). Логарифм от произведения – это сумма логарифмов.
Пример 9. Воспользоваться формулой \(4\). Логарифм от частного – это разность логарифмов.
Пример 10. Формула \(5,6\). Свойства степени.
Логично, что будет выполняться и такое соотношение:
Пример 11. Формулы \(7,8\). Переход к другому основанию.