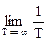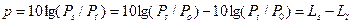ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ СИГНАЛОВ

Математик может говорить все, что взбредет ему в голову, но физик обязан сохранять хотя бы крупицу здравого смысла.
Джосайя Гиббс. Американский физик, XIX в.

Содержание: Введение. 7.1. Мощность и энергия сигналов. 7.2. Энергетические спектры сигналов. Скалярное произведение сигналов. Взаимный энергетический спектр. Энергетический спектр сигнала. Литература.

введение

Понятия мощности и энергии в теории сигналов не относятся к характеристикам каких-либо физических величин сигналов, а являются их количественными характеристиками, отражающими определенные свойства сигналов и динамику изменения их значений во времени, в пространстве или по любым другим аргументам.

Энергия сигналов может быть конечной или бесконечной. Конечную энергию имеют финитные сигналы и сигналы, затухающие по своим значениям в пределах конечной длительности, которые не содержат дельта-функций и особых точек (разрывов второго рода и ветвей, уходящих в бесконечность). В противном случае их энергия равна бесконечности. Бесконечна также энергия периодических сигналов.

7.1. Мощность и энергия сигналов [1,3,16].

Частотное представление применяется не только для спектрального анализа сигналов, но и для упрощения вычислений энергии сигналов и их корреляционных характеристик.

Энергия сигнала равна интегралу от мощности по всему интервалу существования сигнала. В пределе:

Е s =w(t)dt =|s(t)| 2 dt.

По существу, мгновенная мощность является плотностью мощности сигнала, так как измерения мощности возможны только через энергию, выделяемую на определенных интервалах ненулевой длины:

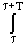
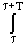
W T ( t ) = (1/T)w(t) dt = (1/T)|s(t)| 2 dt.

Понятие средней мощности может быть распространено и на незатухающие сигналы, энергия которых бесконечно велика. В случае неограниченного интервала Т строго корректное определение средней мощности сигнала производится по формуле:

W s = 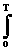w(t) dt.

Энергия и норма сигналов связаны соотношениями:

7.2. Энергетические спектры сигналов [1].

Скалярное произведение сигналов. Энергия суммы двух произвольных сигналов u(t) и v(t) определяется выражением :

E = [u(t)+v(t)] 2 dt = E u + E v + 2u(t)v(t) dt. (7.2.1)

Как следует из этого выражения, энергии сигналов, в отличие от самих сигналов, в общем случае не обладают свойством аддитивности. Энергия суммарного сигнала u(t)+v(t), кроме суммы энергий составляющих сигналов, содержит в себе и так называемую энергию взаимодействия сигналов или взаимную энергию :

E uv = 2u(t)v(t) dt. (7.2.2)

Интеграл выражения (7.2.2) для двух вещественных сигналов является фундаментальной характеристикой, пропорциональной взаимной энергии сигналов. Его называют скалярным произведением сигналов :

Скалярное произведение обладает следующими свойствами :

Линейное пространство сигналов с таким скалярным произведением называется гильбертовым пространством Н. С учетом того, что cos j Ј 1, в гильбертовом пространстве справедливо неравенство Коши-Буняковского :

Для комплексного гильбертова пространства скалярное произведение также представляет собой вещественное число и вычисляется по формуле :

П uv =u(t)v*(t) dt є u*(t)v(t) dt. (7.2.3′)

Из выражения (7.2.3) следует, что косинус угла между сигналами :

cos j = П uv / (||u|| Ч ||v||). (7.2.5)

При полной тождественности сигналов (равенстве амплитуд и временных координат) имеем j = 0, cos j = 1, и скалярное произведение становится равным энергии сигналов:

Взаимный энергетический спектр. Из очевидной однозначности энергии взаимодействия сигналов независимо от формы их математического представления (в динамической и частотной модели) следует выражение для скалярного произведения произвольных вещественных сигналов u(t) и v(t) через спектральные плотности сигналов U( w ) и V( w ) в комплексном гильбертовом пространстве:

W uv ( w ) = U( w )V*( w ), W vu ( w ) = U*( w )V( w ), W uv ( w ) = W vu * ( w ), (7.2.7)

для которых справедливо выражение (7.2.6), называется взаимными энергетическими спектрами вещественных сигналов, и являются функциями распределения плотности энергии взаимодействия сигналов (мощности взаимодействия) по частоте.

В общем случае, за исключением спектров четных функций, взаимные энергетические спектры также являются комплексными функциями:

U( w ) = A u ( w ) + j B u ( w ), V( w ) = A v ( w ) + j B v ( w ).

С учетом четности реальной части и нечетности мнимой части энергетических спектров, интеграл мнимой части выражения (7.2.7′) равен нулю, а, следовательно, скалярное произведение сигналов всегда является вещественным и неотрицательным, как и энергия сигналов:

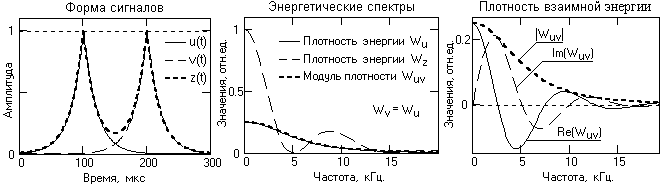
Рис. 7.2.1. Форма и энергетические спектры сигналов.

На рис. 7.2.1 приведена форма двух одинаковых сдвинутых во времени и частично перекрывающихся лапласовских импульсов u(t) и v(t), а также суммарный импульс z(t)=u(t)+v(t). Плотности энергии сигналов W(f) приведены в относительных единицах плотности энергии суммарного сигнала W z (f) на нулевой частоте.

Как видно из графиков, плотности энергии сигналов являются вещественными неотрицательными функциями и содержат только реальные части. В отличие от них, плотность взаимной энергии сигналов является комплексной функцией, при этом модуль плотности по своим значениям на шкале частот соизмерим со средними значениями плотности энергии сигналов на этих частотах и не зависит от их взаимного расположения на временной оси. Для сигналов, одинаковых по форме, модуль взаимной плотности равен значениям плотности энергии сигналов.

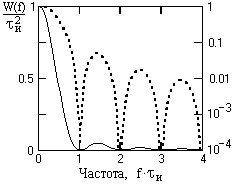
Рис. 7.2.2. Взаимные энергетические спектры сигналов.

На рис. 7.2.2 приведены плотности взаимной энергии тех же сигналов при разной величине временного сдвига D t между сигналами. Однако при постоянном значении модуля взаимной энергии сигналов действительная и мнимая функции спектра мощности существенно изменяются при изменении сдвига между сигналами. При незначительной величине временного перекрытия сигналов частота осцилляций реальной и мнимой части плотности взаимной энергии достаточно велика, а относительный коэффициент затухания колебаний (уменьшение амплитудных значений от периода к периоду) достаточно мал. Соответственно, при вычислении скалярного произведения по формуле (7.2.8) положительные амплитудные значения осцилляций Re(W uv ) практически полностью компенсируются отрицательными значениями и результирующий интеграл, а равно и энергия взаимодействия сигналов (удвоенное значение скалярного произведения), близка к нулевой (стремится к нулю по мере увеличения сдвига между сигналами).

При увеличении степени взаимного перекрытия сигналов частота осцилляций плотности взаимной энергии уменьшается ( D t = 50 mkc на рис. 7.2.2) и основным по энергии реальной части спектра становится центральный низкочастотный пик, площадь которого не компенсируется площадью последующей отрицательной полуволны осцилляции. Соответственно, возрастает и энергия взаимодействия сигналов. При полном перекрытии сигналов (при нулевом фазовом угле между сигналами) осцилляции исчезают, и энергия взаимодействия сигналов максимальна.

Энергетический спектр сигнала. Если функция s(t) имеет фурье-образ S( w ), то плотность мощности сигнала ( спектральная плотность энергии сигнала ) определяется выражением:

w(t) = s(t)s*(t) = |s(t)| 2 Ы |S( w )| 2 = S( w )S*( w ) = W( w ). (7.2.9)

W uv ( w ) = U( w )V*( w ) = U( w )U*( w ) = |U( w )| 2 = W u ( w ). (7.2.10)

Соответственно, полная энергия сигнала:

Для произвольного сигнала s(t) равенство

|s(t)| 2 dt =|S(f)| 2 df

обычно называют равенством Парсеваля (в математике – теоремой Планшереля, в физике – формулой Релея). Равенство очевидно, так как координатное и частотное представления по существу только разные математические отображения одного и того же сигнала. Аналогично для энергии взаимодействия двух сигналов:

u(t) v*(t) dt =U(f) V*(f) df.

Из равенства Парсеваля следует инвариантность скалярного произведения сигналов и нормы относительно преобразования Фурье:

В целом ряде чисто практических задач регистрации и передачи сигналов энергетический спектр сигнала имеет весьма существенное значение.

Периодические сигналы переводятся в спектральную область в виде рядов Фурье. Запишем периодический сигнал с периодом Т в виде ряда Фурье в комплексной форме:

s(t) =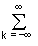S k exp(j2 p kt/T),

и вычислим среднюю мощность сигнала за один период:

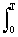
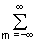
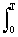
W T = (1/T)s 2 (t) dt = (1/T)S k S m exp(j2 p( k+m)t/T) dt.

Интегрированием энергетического спектра по интервалам лепестков спектра нетрудно вычислить, что в пределах первого лепестка сосредоточено 90.2% энергии всего сигнала, в пределах второго – 4.8%, в пределах третьего – 1.7%, и т.д. Если форма сигналов в пункте их приема (детектирования) существенного значения не имеет, а регистрация сигналов идет на уровне статистических шумов, равномерно распределенных по всему частотному диапазону, то такие сигналы целесообразно пропускать через фильтр нижних частот с выделением только первого энергетического лепестка сигнала. Естественно, что при этом фронты регистрируемого сигнала будут сглажены. Но при расширении полосы пропускания фильтра на два или три лепестка энергия принимаемого сигнала будет увеличена соответственно на 4.8 или 6.5%, в то время как энергия шумов в 2 или 3 раза.

Источник

Мощность и энергия сигналов

Понятия мощности и энергиив теории сигналов не относятся к характеристикам каких-либо физических величин сигналов, а являются их количественными характеристиками, отражающими определенные свойства сигналов и динамику изменения их значений (отсчетов) во времени, в пространстве или по любым другим аргументам.

Для произвольного, в общем случае комплексного, сигнала s(t) = a(t)+jb(t), где а(t) и b(t) – вещественные функции, мгновенная мощность (instantaneous power) сигнала по определению задается выражением:

т.е. функция распределения мгновенной мощности по аргументу сигнала равна квадрату функции его модуля, для вещественных сигналов – квадрату функции амплитуд.

Аналогично для дискретных сигналов:

Энергия сигнала (также по определению) равна интегралу от мощности по всему интервалу существования или задания сигнала. В пределе:

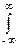
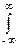
Е_s =w(t)dt =|s(t)| 2 dt. (2.10)

Мгновенная мощность w(t) является плотностью мощности сигнала, так как измерения мощности возможны только через энергию на интервалах ненулевой длины:

w(t) = (1/Dt)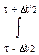|s(t)| 2 dt.

Энергия сигналов может быть конечной или бесконечной. Конечную энергию имеют финитные сигналы и сигналы, затухающие по своим значениям в пределах конечной длительности, которые не содержат дельта-функций и особых точек (разрывов второго рода и ветвей, уходящих в бесконечность). В противном случае их энергия равна бесконечности. Бесконечна также энергия периодических сигналов.

Как правило, сигналы изучаются на определенном интервале Т, для периодических сигналов – в пределах одного периода Т, при этом средняя мощность (average power) сигнала:

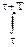
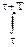
W_T(t) = (1/T)w(t) dt = (1/T)|s(t)| 2 dt. (2.11)

Понятие средней мощности может быть распространено и на незатухающие сигналы, энергия которых бесконечно велика. В случае неограниченного интервала Т строго корректное определение средней мощности сигнала должно производиться по формуле:

W_s = 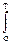w(t) dt. (2.11′)

Квадратный корень из значения средней мощности характеризует действующее (среднеквадратическое) значение сигнала (root mean sqare, RMS).

Применительно к электрофизическим системам, данным понятиям мощности и энергии соответствуют вполне конкретные физические величины. Допустим, что функцией s(t) отображается электрическое напряжение на резисторе, сопротивление которого равно R Ом. Тогда рассеиваемая в резисторе мощность, как известно, равна (в вольт-амперах):

а полная выделенная на резисторе тепловая энергия определяется соответствующим интегрированием мгновенной мощности w(t) по интервалу задания напряжения s(t) на резисторе R. Физическая размерность мощности и энергии в этом случае определяется соответствующей физической размерностью функции напряжения s(t) и сопротивления резистора R. Для безразмерной величины s(t) при R=1 это полностью соответствует выражению (2.2.1). В теории сигналов в общем случае сигнальные функции s(t) не имеют физической размерности, и могут быть формализованным отображением любого процесса или распределения какой-либо физической величины, при этом понятия энергии и мощности сигналов используются в более широком смысле, чем в физике. Они представляют собой метрологические характеристики сигналов.

Из сравнения выражений (2.9) и (2.10) следует, что энергия и норма сигнала связаны соотношениями:

Пример.Цифровой сигнал задан функцией s(n) = <0,1,2,3,4,5,4,3,2,1,0,0,0,0. >.

Энергия сигнала: E_s = 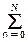s 2 (n) = 1+4+9+16+25+16+9+4+1 = 85.

Норма: ||s(n)|| = 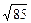» 9.22

Вычислим энергию суммы двух произвольных сигналов u(t) и v(t):

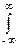
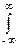
E =[u(t)+v(t)] 2 dt = E_u + E_v + 2u(t)v(t) dt. (2.13)

Как следует из этого выражения, энергия сигналов (а равно и их мощность), в отличие от самих сигналов, в общем случае не обладают свойством аддитивности. Энергия суммарного сигнала u(t)+v(t), кроме суммы энергий составляющих сигналов, содержит в себе и так называемую энергию взаимодействия сигналов или взаимную энергию:

E_uv = 2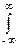u(t)v(t) dt. (2.14)

Нетрудно заметить, что энергия взаимодействия сигналов равна их удвоенному скалярному произведению:

При обработке данных используются также понятия мощности взаимодействия двух сигналов x(t) и y(t):

Для вещественных сигналов:

С использованием выражений (2.15-2.16) интегрированием по соответствующим интервалам вычисляются значения средней мощности взаимодействия сигналов на определенных интервалах Т и энергия взаимодействия сигналов.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ И ПОМЕХ

Энергетические характеристики. Основными энер­гетическими характеристиками вещественного сигнала s(t) явля­ются его мощность и энергия.

Если S(t) — напряжение u(t) или ток i(t), то мгновенная мощ­ность, выделяемая на активном сопротивлении R, определяется через квадрат мгновенного значения

Обычно в теории электросвязи принимают R=l Ом (кроме особо оговариваемых случаев), и тогда в общем виде

Принятие такого условия связано с тем, что, как правило, инте­ресуются не конкретным значением мощности, а отношениями мощностей сигнала и помехи. При вычислении отношения сопро­тивление R сокращается и для упрощения вычислений его можно принять единичным.

Энергия сигнала на интервале (t_1, t₂) определяется как интег­рал от мгновенной мощности

(2.26)
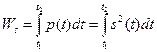
Отношение

(2.27)

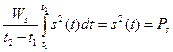
имеет смысл средней мощности P_s = s 2 (/) на интервале t₁. t₂—Напомним, что волнистая черта означает усреднение по времени. Для случайных сигналов (помех) среднюю мощность можно вы­числить по спектральной плотности мощности Gx(f)- Поскольку функция G_x(f) показывает распределение мощности по частотам (см. (2.22)), полная мощность выражается интегралом

(2.28)

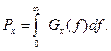
Чтобы найти, например, мощность случайного сигнала (поме­хи), заключенную в полосе частот f₁. f₂, надо провести интегри­рование (2.28) в этой полосе:

(2.29)

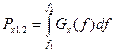
Устанавливая в (2.29) пределы интегрирования от f до f+ получим сред­нюю мощность шума

(2.30)

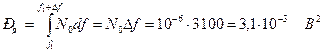
Распределение мощности в спектре периоди­ческого сигнала. Средняя мощность периодического сиг­нала, рассматриваемая на всей оси времени, совпадает со средней мощностью за период Т.

Для гармонического сигнала u(t)=u_mcos(wt+y₀) согласнo(2.27) средняя мощность

(2.31)

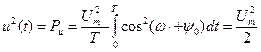
не зависит ни от частоты, ни от начальной фазы.

Поскольку периодический сигнал s(t) можно представить в ви­де тригонометрического ряда Фурье (2.6) и интеграл суммы ра­вен сумме интегралов, из (2.27) и (2.31) следует

(2.32)

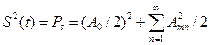
Децибелы, опре­деленные относительно уровня Р_о = 1 мВт, называются децибел-милливаттом и обозначаются дБм.

При логарифмической единице измерения уровней такая ха­рактеристика качества, как отношение сигнал-помеха будет равна разности уровней сигнала L_s и помехи L_n, так как динамический диапазон и коэффициент амп­литуд ы.

Динамический диапазон D_s, дБ, характеризует пределы изменения мгновенной мощности и определяется выражением:

Коэффициентом амплитуды сигнала К 2 _А называется отношение его максимальной мощности к средней. В логарифмических еди­ницах, дБ,

K 2 _A=10lg(pmax/P)(2.33)

В некоторых случаях динамический диапазон и коэффициенты амплитуды определяются не в логарифмических, а в абсолютных единицах (в «разах»).

Длительность и ширина спектра с и г н а л а. Под длительностью сигнала понимают интервал времени его сущест­вования. Вычисляется как разность между временем окончания сигнала t₂ и временем его начала t_1:

Ширина спектра — это интервал частот, занимаемый спектром сигнала. Вычисляется как разность между максимальной частотой спектра сигнала fmax и минимальной fmin’

Вычисление длительности и ширины спектра сигнала не вызы­вает трудностей, если сигнал имеет четко выраженные начало и конец, а спектр — граничные частоты. Но из преобразования Фурье следует, что если сигнал имеет конечную длительность, то спектр его бесконечный. И наоборот. В этом случае необходимо условиться об определении длительности и ширины спектра.

В практике применяются различные определения, выбор кото­рых зависит от назначения сигнала, его формы, структуры спект­ра. В некоторых случаях выбор даже произволен. Наибольшее применение нашли следующие способы определения Dt_s и Df_s.

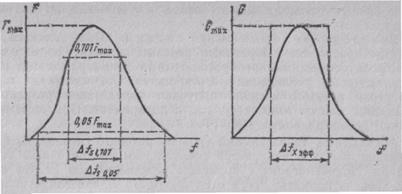
1. Отсчет на заданном уровне от максимального. Обычно дли­тельность импульсного сигнала и ширину его спектра определяют на уровне 1/ 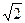от максимального значения соответственно s(t) или F(w). Но можно выбрать для вычислений любой другой уро­вень, например 5% максимального, как показано на рис. 2.18.

2. Энергетический способ. За длительность сигнала (ширину спектра) принимают такой интервал времени (частот), в который попадает заданная часть полной энергии сигнала, например 0,9
или 0,95.

3. Замена реального сигнала (спектра) равновеликим прямо­угольным. Такая процедура показана на рис. 2.19, где изображе­на спектральная плотность мощности случайного сигнала Gx(f). Площади прямоугольника и фигуры, ограниченной кривой Gx(f)

Рис. 2.18. Определение ширины Рис. 2.19. К определению

спектра на заданном уровне эффективной ширины спект-

ра методом равновеликого прямоугольника

Из рисунка следует, что ширина спектра, называемая эффективной.

Числовые характеристики сигналов и помех широко использу­ются в электросвязи. По энергетическим характеристикам опре­деляется требуемое превышение сигнала над помехой, по ширине спектра сигнала устанавливается полоса пропускания канала электросвязи, необходимая для неискаженной передачи. Для не­прерывных первичных сигналов ширина спектра определяется обычно опытным путем (см. § 2.9). Для импульсных сигналов приопределении ширины спектра можно воспользоваться важней­шим положением теории сигналов: если oзначает ширину спек­тра некоторого сигнала длительностью Dt_s то всегда имеет место соотношение

где μ— постоянная величина, порядка единицы (μ≈1) для видео-

импульсов и порядка двух (μ≈2) для радиоимпульсов. Смысл

єтого соотношения состоит в том, что ширина спектра сигнала обратно пропорциональна его длительности.

Источник