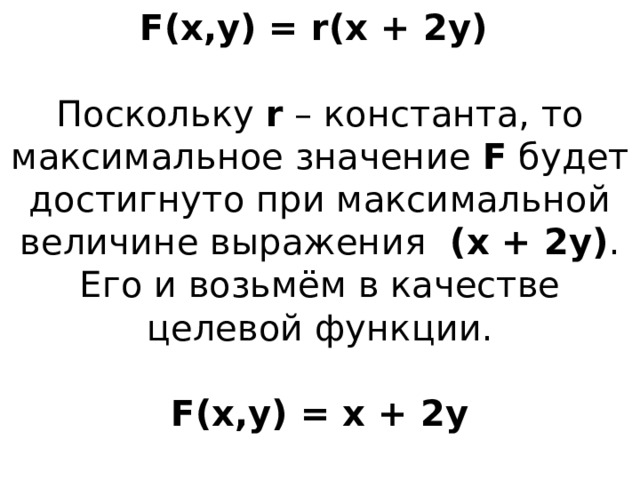что такое модель оптимального планирования
Содержание урока
Оптимальное планирование
Модели оптимального планирования (§20)
Оптимальное планирование
Проблема, к обсуждению которой мы теперь переходим, называется оптимальным планированием. Объектами планирования могут быть самые разные системы: деятельность отдельного предприятия, отрасли промышленности или сельского хозяйства, региона, наконец государства. Постановка задачи планирования выглядит следующим образом:
• имеются некоторые плановые показатели: X, Y, и др.;
• имеются некоторые ресурсы: R1, R2 и др., за счет которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены;
• имеется определенная стратегическая цель, зависящая от значений X, Y и др. плановых показателей, на которую следует ориентировать планирование.
Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Это и будет оптимальным планом.
Приведем примеры. Пусть объектом планирования является детский сад. Ограничимся лишь двумя плановыми показателями: количеством детей и количеством воспитателей. Основными ресурсами деятельности детского сада являются объем финансирования и площади помещения. А каковы стратегические цели?
Естественно, одной из них является сохранение и укрепление здоровья детей. Количественной мерой такой цели является минимизация заболеваемости воспитанников детского сада.
Другой пример: планирование экономической деятельности государства. Безусловно, это слишком сложная задача для того, чтобы нам с ней полностью разобраться. Плановых показателей очень много: это производство различных видов промышленной и сельскохозяйственной продукции, подготовка специалистов, выработка электроэнергии, размер зарплаты работников бюджетной сферы и многое другое. К ресурсам относятся: количество работоспособного населения, бюджет государства, природные ресурсы, энергетика, возможности транспортных систем и пр. Как вы понимаете, каждый из этих видов ресурсов ограничен. Кроме того, важнейшим ресурсом является время, отведенное на выполнение плана. Вопрос о стратегических целях довольно сложный. У государства их много, но в разные периоды истории приоритеты целей могут меняться.
Например, в военное время главной целью является максимальная обороноспособность, военная мощь страны. В мирное время в современном цивилизованном государстве приоритетной целью должно быть достижение максимального уровня жизни населения.
Если мы хотим использовать компьютер для решения задачи оптимального планирования, то нам снова нужно построить математическую модель. Следовательно, всё, о чем говорилось в примерах, должно быть переведено на язык чисел, формул, уравнений и других средств математики. В полном объеме для реальных систем эта задача очень сложная. Как и раньше, мы пойдем по пути упрощения. Рассмотрим очень простой пример, из которого вы получите представление об одном из подходов к решению задачи оптимального планирования.
Пример. Школьный кондитерский цех готовит пирожки и пирожные. В силу ограниченности емкости склада за день можно приготовить в совокупности не более 700 штук изделий. Рабочий день в кондитерском цехе длится 8 часов. Производство пирожных более трудоемко, поэтому если выпускать только их, за день можно произвести не более 250 штук, пирожков же можно произвести 1000 штук (если при этом не выпускать пирожных). Стоимость пирожного вдвое выше, чем стоимость пирожка. Требуется составить такой дневной план производства, чтобы обеспечить наибольшую выручку кондитерского цеха.
Разумеется, это чисто учебный пример. Вряд ли существует такой кондитерский цех, который выпускает всего два вида продукции, да и наибольшая выручка — не единственная цель его работы. Но зато математически формулировка задачи будет простой. Давайте ее выработаем.
Плановыми показателями являются:
• х — дневной план выпуска пирожков;
• у — дневной план выпуска пирожных.
Что в этом примере можно назвать ресурсами производства? Из того, о чем говорится в условии задачи, это:
• длительность рабочего дня — 8 часов;
• вместимость складского помещения — 700 мест.
Предполагается для простоты, что другие ресурсы (сырье, электроэнергия и пр.) не ограничены. Формализацию цели (достижение максимальной выручки цеха) мы обсудим позже.
Получим соотношения, следующие из условий ограниченности времени работы цеха и вместимости склада, т. е. суммарного числа изделий.
Из постановки задачи следует, что на изготовление одного пирожного затрачивается в 4 раза больше времени, чем на выпечку одного пирожка. Если обозначить время изготовления пирожка как t мин, то время изготовления пирожного будет равно 41 мин. Значит, суммарное время на изготовление х пирожков и у пирожных равно
tx + 4ty = (х + 4y)t.
Но это время не может быть больше длительности рабочего дня. Отсюда следует неравенство:
(х + 4y)t ≤ 8 • 60,
(х + 4y)t ≤ 480.
Легко посчитать t — время изготовления одного пирожка. Поскольку за рабочий день их может быть изготовлено 1000 штук, на один пирожок тратится 480/1000 = 0,48 мин. Подставляя это значение в неравенство, получим:
(х + 4у) • 0,48 ≤ 480.
х + 4у ≤ 1000.
Ограничение на общее число изделий дает совершенно очевидное неравенство:
х + у ≤ 700.
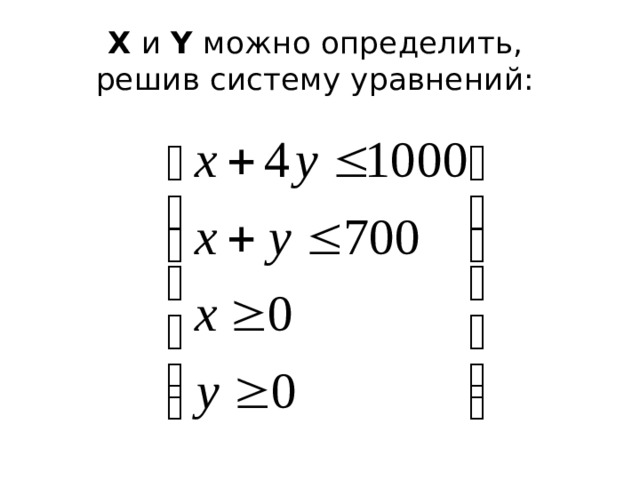
К двум полученным неравенствам следует добавить условия положительности значений величин х и у (не может быть отрицательного числа пирожков и пирожных). В итоге получим систему неравенств:
Следующая страница 
Целевая функция
Модели оптимального планирования
Презентация по учебнику информатики для 10-11 классов авторов Семакин И.Г., Хеннер Е.К. Модели оптимального планирования..
Просмотр содержимого документа
«Модели оптимального планирования»
Модели оптимального планирования
Постановка задачи планирования
Объект планирования: ДЕТСКИЙ САД
Объект планирования: Кондитерский цех
Если мы хотим использовать компьютер для решения задачи, то нам нужно построить мат.модель!
X и Y можно определить, решив систему уравнений:
Формализация цели (max выручка):
Если мы хотим использовать компьютер для решения задачи, то нам нужно построить мат.модель!
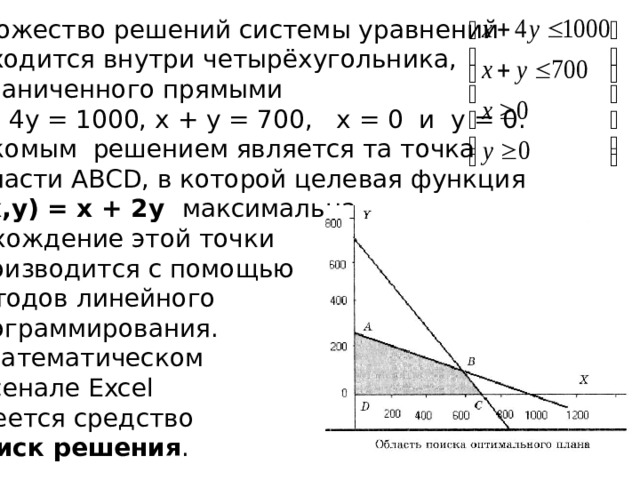
Множество решений системы уравнений
находится внутри четырёхугольника, ограниченного прямыми x + 4y = 1000, x + y = 700, x = 0 и y = 0.
Искомым решением является та точка области ABCD, в которой целевая функция
§ 20. Модели оптимального планирования
Проблема, к обсуждению которой мы теперь переходим, называется оптимальным планированием. Объектами планирования могут быть самые разные системы: деятельность отдельного предприятия, отрасли промышленности или сельского хозяйства, региона, наконец государства. Постановка задачи планирования выглядит следующим образом:
Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Это и будет оптимальным планом.
Приведем примеры. Пусть объектом планирования является детский сад. Ограничимся лишь двумя плановыми показателями: количеством детей и количеством воспитателей. Основными ресурсами деятельности детского сада являются объем финансирования и площади помещения. А каковы стратегические цели? Естественно, одной из них является сохранение и укрепление здоровья детей. Количественной мерой такой цели является минимизация заболеваемости воспитанников детского сада.
Другой пример: планирование экономической деятельности государства. Безусловно, это слишком сложная задача для того, чтобы нам с ней полностью разобраться. Плановых показателей очень много: это производство различных видов промышленной и сельскохозяйственной продукции, подготовка специалистов, выработка электроэнергии, размер зарплаты работников бюджетной сферы и многое другое. К ресурсам относятся: количество работоспособного населения, бюджет государства, природные ресурсы, энергетика, возможности транспортных систем и пр. Как вы понимаете, каждый из этих видов ресурсов ограничен. Кроме того, важнейшим ресурсом является время, отведенное на выполнение плана. Вопрос о стратегических целях довольно сложный. У государства их много, но в разные периоды истории приоритеты целей могут меняться. Например, в военное время главной целью является максимальная обороноспособность, военная мощь страны. В мирное время в современном цивилизованном государстве приоритетной целью должно быть достижение максимального уровня жизни населения.
Если мы хотим использовать компьютер для решения задачи оптимального планирования, то нам снова нужно построить математическую модель. Следовательно, всё, о чем говорилось в примерах, должно быть переведено на язык чисел, формул, уравнений и других средств математики. В полном объеме для реальных систем эта задача очень сложная. Как и раньше, мы пойдем по пути упрощения. Рассмотрим очень простой пример, из которого вы получите представление об одном из подходов к решению задачи оптимального планирования.
Пример. Школьный кондитерский цех готовит пирожки и пирожные. В силу ограниченности емкости склада за день можно приготовить в совокупности не более 700 штук изделий. Рабочий день в кондитерском цехе длится 8 часов. Производство пирожных более трудоемко, поэтому если выпускать только их, за день можно произвести не более 250 штук, пирожков же можно произвести 1000 штук (если при этом не выпускать пирожных). Стоимость пирожного вдвое выше, чем стоимость пирожка. Требуется составить такой дневной план производства, чтобы обеспечить наибольшую выручку кондитерского цеха.
Разумеется, это чисто учебный пример. Вряд ли существует такой кондитерский цех, который выпускает всего два вида продукции, да и наибольшая выручка — не единственная цель его работы. Но зато математически формулировка задачи будет простой. Давайте ее выработаем.
Предполагается для простоты, что другие ресурсы (сырье, электроэнергия и пр.) не ограничены. Формализацию цели (достижение максимальной выручки цеха) мы обсудим позже.
Получим соотношения, следующие из условий ограниченности времени работы цеха и вместимости склада, т. е. суммарного числа изделий.
Из постановки задачи следует, что на изготовление одного пирожного затрачивается в 4 раза больше времени, чем на выпечку одного пирожка. Если обозначить время изготовления пирожка как t мин, то время изготовления пирожного будет равно 4t мин. Значит, суммарное время на изготовление х пирожков и у пирожных равно
Но это время не может быть больше длительности рабочего дня. Отсюда следует неравенство:
Легко посчитать t — время изготовления одного пирожка. Поскольку за рабочий день их может быть изготовлено 1000 штук, на один пирожок тратится 480/1000 = 0,48 мин. Подставляя это значение в неравенство, получим:
Ограничение на общее число изделий дает совершенно очевидное неравенство:
К двум полученным неравенствам следует добавить условия положительности значений величин х и у (не может быть отрицательного числа пирожков и пирожных). В итоге получим систему неравенств:
А теперь перейдем к формализации стратегической цели: получению максимальной выручки. Выручка — это стоимость всей проданной продукции. Пусть цена одного пирожка — r рублей. По условию задачи, цена пирожного в два раза больше, т. е. 2r рублей. Отсюда стоимость всей произведенной за день продукции равна
Целью производства является получение максимальной выручки. Будем рассматривать записанное выражение как функцию от х, у:
Она называется целевой функцией.
Поскольку значение r — константа, максимальное значение F(x, у) будет достигнуто при максимальной величине выражения (х + 2у). Поэтому в качестве целевой функции можно принять
Следовательно, получение оптимального плана свелось к следующей математической задаче:
Требуется найти значения плановых показателей х и у, удовлетворяющих данной системе неравенств (1) и придающих максимальное значение целевой функции (2).
Итак, математическая модель задачи оптимального планирования для школьного кондитерского цеха построена.
Теперь следующий вопрос: как решить эту задачу? Вы уже догадываетесь, что решать ее за нас будет компьютер с помощью табличного процессора Excel. А мы обсудим лишь подход к решению, не вникая в подробности метода.
Математическая дисциплина, которая посвящена решению таких задач, называется математическим программированием. А поскольку в целевую функцию f(x, у) величины х и у входят линейно (т. е. в первой степени), наша задача относится к разделу этой науки, который называется линейным программированием.
Система написанных выше неравенств представляется на координатной плоскости четырехугольником, ограниченным четырьмя прямыми, соответствующими линейным уравнениям:
На рис. 3.10 эта область представляет собой четырехугольник ABCD и выделена заливкой. Любая точка четырехугольника является решением системы неравенств (1). Например, х = 200, у = 100. Этой точке соответствует значение целевой функции f(200, 100) = 400. А другой точке (х = 600, у = 50) соответствует f(600, 50) = 700. Но, очевидно, искомым решением является та точка области ABCD, в которой целевая функция максимальна. Нахождение этой точки производится с помощью методов линейного программирования.
Рис. 3. 10. Область поиска оптимального плана
В математическом арсенале Excel имеется средство Поиск решения. Как решать данную задачу с помощью этого средства, вы узнаете из компьютерного практикума.
В результате решения задачи получается следующий оптимальный план дневного производства кондитерского цеха: нужно выпускать 600 пирожков и 100 пирожных. Эти плановые показатели соответствуют координатам точки В на рис. 3.10. В этой точке значение целевой функции f(600, 100) = 800. Если один пирожок стоит 5 рублей, то полученная выручка составит 4000 рублей.
Система основных понятий
Вопросы и задания
б) Внесите изменение в постановку задачи оптимального планирования из этого параграфа для двух видов продукции с учетом еще одного ограничения: число пирожных должно быть не меньше числа пирожков. На координатной плоскости постройте область поиска решения.
Презентация по информатике по теме «Модели оптимального планирования»
Описание презентации по отдельным слайдам:
МОДЕЛИ ОПТИМАЛЬНОГО ПЛАНИРОВАНИЯ
А теперь перейдем к формализации стратегической цели: получению максимальной выручки. Выручка — это стоимость всей проданной продукции. Пусть цена одного пирожка — r рублей. По условию задачи, цена пирожного в два раза больше, т. е. 2r рублей. Отсюда стоимость всей произведенной за день продукции равна rх + 2rу = r(х + 2у). Целью производства является получение максимальной выручки. Будем рассматривать записанное выражение как функцию от х, у: F(x, у) = r(х + 2у). Она называется целевой функцией. Поскольку значение r — константа, максимальное значение F(x, у) будет достигнуто при максимальной величине выражения (х + 2у). Поэтому в качестве целевой функции можно принять f(x, у) = х + 2у. Следовательно, получение оптимального плана свелось к следующей математической задаче: Требуется найти значения плановых показателей х и у, удовлетворяющих данной системе неравенств и придающих максимальное значение целевой функции. ЦЕЛЕВАЯ ФУНКЦИЯ
А теперь перейдем к формализации стратегической цели: получению максимальной выручки. Выручка — это стоимость всей проданной продукции. Пусть цена одного пирожка — r рублей. По условию задачи, цена пирожного в два раза больше, т. е. 2r рублей. Отсюда стоимость всего rх + 2rу = r(х + 2у). Целью производства является получение максимальной выручки. Будем рассматривать записанное выражение как функцию от х, у: F(x, у) = r(х + 2у). Она называется целевой функцией. Поскольку значение r — константа, максимальное значение F(x, у) будет достигнуто при максимальной величине выражения (х + 2у). Поэтому в качестве целевой функции можно принять f(x, у) = х + 2у. Следовательно, получение оптимального плана свелось к следующей математической задаче: Требуется найти значения плановых показателей х и у, удовлетворяющих данной системе неравенств и придающих максимальное значение целевой функции. ЦЕЛЕВАЯ ФУНКЦИЯ
Система написанных неравенств представляется на координатной плоскости четырехугольником, ограниченным четырьмя прямыми, соответствующими линейным уравнениям: х + 4у = 1000, х + у = 700, х = 0 (ось У). у = 0 (ось X) Искомым решением является та точка области ABCD, в которой целевая функция максимальна. Нахождение этой точки производится с помощью методов линейного программирования. В математическом арсенале Excel имеется средство Поиск решения. Как решать данную задачу с помощью этого средства, вы узнаете из компьютерного практикума. В результате решения получается следующий оптимальный план : нужно выпускать 600 пирожков и 100 пирожных. Если один пирожок стоит 5 рублей, то полученная выручка составит 4000 рублей.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс профессиональной переподготовки
Методическая работа в онлайн-образовании
Курс профессиональной переподготовки
Математика и информатика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-628227
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
На новом «Уроке цифры» школьникам расскажут о разработке игр
Время чтения: 1 минута
В МГУ разрабатывают школьные учебники с дополненной реальностью
Время чтения: 2 минуты
Российские школьники установили рекорд на олимпиаде по астрономии
Время чтения: 2 минуты
Российские адвокаты бесплатно проконсультируют детей 19 ноября
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Педагогов и учеников предлагают тренировать на случай нападения
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Конспект урока по информатике на тему «Модели оптимального планирования. Стратегическая цель планирования. Задача линейного программирования для нахождения оптимального плана» (11 класс)
Урок №__________11 класс Дата___________
Конспект урока по информатике
Тема: «Модели оптимального планирования. Стратегическая цель планирования. Задача линейного программирования для нахождения оптимального плана»
Цель урока : научить учащихся решать задачи оптимального планирования средствами MS Excel.
образовательная : познакомить учащихся с особым видом экономических задач – задач оптимального планирования, способом их решения в среде MS Excel;
развивающая: закрепить навыки работы с формулами в среде электронных таблиц; развивать умение анализировать и обобщать материал, строить математическую модель задачи;
воспитательная: воспитывать самостоятельность и ответственность в принятии решения.
Оборудование: компьютер учителя, компьютеры учащихся, Программное обеспечение: MS PowerPoint, MS Excel, доска, проектор, тетради, учебники
Актуализация опорных знаний и умений.
а) Что такое корреляционная зависимость?
б) Что такое корреляционный анализ?
в) Какие типы задач можно решать с помощью корреляционного анализа?
г) Какая величина является количественной мерой корреляции? Какие значения она может принимать?
д) С помощью какого средства табличного процессора можно вычислить коэффициент корреляции?
е) Для данных из таблицы, представленной на рис. 2.18, постройте две линейные регрессионные модели.
ж) Для этих же данных вычислите коэффициент корреляции. Сравните с приведенными на рис. 2.18 результатами.
3. Изучение нового материала.
Объектами планирования могут быть самые разные системы: деятельность отдельного предприятия, отрасли промышленности или сельского хозяйства, региона, наконец государства.
Постановка задачи планирования выглядит следующим образом:
имеются некоторые плановые показатели: X, У, и др.;
имеются некоторые ресурсы: R1, R2 и др., за счет которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены;
имеется определенная стратегическая цель, зависящая от значений X, У и др. плановых показателей, на которую следует ориентировать планирование.
Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Это и будет оптимальным планом.
Приведём примеры. Пусть объектом планирования является детский сад. Ограничимся лишь двумя плановыми показателями: количеством детей и количеством воспитателей. Основными ресурсами деятельности детского сада являются объем финансирования и площади помещения. А каковы стратегические цели? Естественно, одной из них является сохранение и укрепление здоровья детей. Количественной мерой такой цели является минимизация заболеваемости воспитанников детского сада.
Другой пример: планирование экономической деятельности государства. Безусловно, это слишком сложная задача для того, чтобы нам с ней полностью разобраться. Плановых показателей очень много: это производство различных видов промышленной и сельскохозяйственной продукции, подготовка специалистов, выработка электроэнергии, размер зарплаты работников бюджетной сферы и многое другое. К ресурсам относятся: количество работоспособного населения, бюджет государства, природные ресурсы, энергетика, возможности транспортных систем и пр.
Как вы понимаете, каждый из этих видов ресурсов ограничен. Кроме того, важнейшим ресурсом является время, отведенное на выполнение плана. Вопрос о стратегических целях довольно сложный. У государства их много, но в разные периоды истории приоритеты целей могут меняться. Например, в военное время главной целью является максимальная обороноспособность, военная мощь страны. В мирное время в современном цивилизованном государстве приоритетной целью должно быть достижение максимального уровня жизни населения.
Если мы хотим использовать компьютер для решения задачи оптимального планирования, то нам снова нужно построить математическую модель. Следовательно, все, о чем говорилось в примерах, должно быть переведено на язык чисел, формул, уравнений и других средств математики. В полном объеме для реальных систем эта задача очень сложная. Как и раньше, мы пойдем по пути упрощения. Рассмотрим очень простой пример, из которого вы получите представление об одном из подходов к решению задачи оптимального планирования.
Пример. Школьный кондитерский цех готовит пирожки и пирожные. В силу ограниченности емкости склада за день можно приготовить в совокупности не более 700 штук изделий. Рабочий день в кондитерском цехе длится 8 часов. Поскольку производство пирожных более трудоемко, то если выпускать только их, за день можно произвести не более 250 штук, пирожков же можно произвести 1000 штук (если при этом не выпускать пирожных). Стоимость пирожного вдвое выше, чем стоимость пирожка. Требуется составить такой дневной план производства, чтобы обеспечить наибольшую выручку кондитерского цеха.
Разумеется, это чисто учебный пример. Вряд ли существует такой кондитерский цех, который выпускает всего два вида продукции, да и наибольшая выручка — не единственная цель его работы. Но зато математически формулировка задачи будет простой. Давайте ее выработаем.
Плановыми показателями являются:
х — дневной план выпуска пирожков;
у — дневной план выпуска пирожных.
Что в этом примере можно назвать ресурсами производства? Из того, о чем говорится в условии задачи, это:
длительность рабочего дня — 8 часов;
вместимость складского помещения — 700 мест.
Предполагается для простоты, что другие ресурсы (сырье, электроэнергия и пр.) не ограничены. Формализацию цели (достижение максимальной выручки цеха) мы обсудим позже.
Получим соотношения, следующие из условий ограниченности времени работы цеха и вместимости склада, т. е. суммарного числа изделий.
Из постановки задачи следует, что на изготовление одного пирожного затрачивается в 4 раза больше времени, чем на выпечку одного пирожка. Если обозначить время изготовления пирожка как t мин, то время изготовления пирожного будет равно 41 мин. Значит, суммарное время на изготовление х пирожков и у пирожных равно
Но это время не может быть больше длительности рабочего дня. Отсюда следует неравенство:
Легко посчитать t — время изготовления одного пирожка. Поскольку за рабочий день их может быть изготовлено 1000 штук, то на один пирожок тратится 480/1000 = 0,48 мин. Подставляя это значение в неравенство, получим:
Ограничение на общее число изделий дает совершенно очевидное неравенство:
К двум полученным неравенствам следует добавить условия положительности значений величин х и у (не может быть отрицательного числа пирожков и пирожных). В итоге получим систему неравенств:
А теперь перейдем к формализации стратегической цели : получению максимальной выручки. Выручка — это стоимость всей проданной продукции. Пусть цена одного пирожка — г рублей. По условию задачи, цена пирожного в два раза больше, т. е. 2r рублей.
Отсюда стоимость всей произведенной за день продукции равна
Целью производства является получение максимальной выручки. Будем рассматривать записанное выражение как функцию от х, у:
Она называется целевой функцией.
Поскольку значение r — константа, то максимальное значение F(x, у) будет достигнуто при максимальной величине выражения (х + 2у). Поэтому в качестве целевой функции можно принять
Следовательно, получение оптимального плана свелось к следующей математической задаче:
Требуется найти значения плановых показателей х и у, удовлетворяющих данной системе неравенств и придающих максимальное значение целевой функции.
Итак, математическая модель задачи оптимального планирования для школьного кондитерского цеха построена.
Теперь следующий вопрос: как решить эту задачу?
Вы уже догадываетесь, что решать ее за нас будет компьютер с помощью табличного процессора Excel. А мы обсудим лишь подход к решению, не вникая в подробности метода.
Математическая дисциплина, которая посвящена решению таких задач, называется математическим программированием. А поскольку в целевую функцию f(x, у) величины х и у входят линейно (т. е. в первой степени), то наша задача относится к разделу этой науки, который называется линейным программированием.
Система написанных выше неравенств представляется на координатной плоскости четырехугольником, ограниченным четырьмя прямыми, соответствующими линейным уравнениям:
х + 4у = 1000,
х + у = 700,
х = 0 (ось Y),
у = 0 (осьХ).
На рис. 6.9 эта область представляет собой четырехугольник ABCD и выделена заливкой. Любая точка четырехугольника является решением системы неравенств.
Например, х = 200, у = 100.
Этой точке соответствует значение целевой функции f(200, 100) = 400. А другой точке
(х = 600, у = 50) соответствует f(600, 50) = 700. Но, очевидно, искомым решением является та точка области ABCD, в которой целевая функция максимальна. Нахождение этой точки производится с помощью методов линейного программирования.
В результате решения задачи получается следующий оптимальный план дневного производства кондитерского цеха: нужно выпускать 600 пирожков и 100 пирожных. Эти плановые показатели соответствуют координатам точки В на рис. 6.9. В этой точке значение целевой функции f(600, 100) = 800. Если один пирожок стоит 5 рублей, то полученная выручка составит 4000 рублей.
4.Подведение итогов урока, выставление оценок
Сегодня мы с вами узнали, что такое оптимальное планирование, получили представление о решении задач оптимального планирования, закрепили на практике знания и навыки работы с надстройкой «Поиск решения» в MS Excel, выработали навыки работы с задачами оптимального планирования в MS Excel.
Система основных понятий
5. Домашнее задание:
Читать §_________с.______________, отвечать на вопросы._________________________________