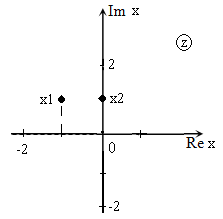что такое мнимые корни квадратного уравнения

Квадратное уравнение с комплексными корнями

Вы будете перенаправлены на Автор24

Рассмотрим решение уравнений с комплексными корнями и коэффициентами.

Рассмотрим три случая:

\[x_ <1>=\sqrt[<3>] <8>\cdot \left(\cos \frac<2\pi > <3>+i\cdot \sin \frac<2\pi > <3>\right)=\sqrt[<3>] <8>\cdot (-\frac<1> <2>+\frac <\sqrt<3>> <2>\cdot i)=2\cdot (-\frac<1> <2>+\frac <\sqrt<3>> <2>\cdot i)=-1+\sqrt <3>\cdot i.\]

\[x_ <2>=\sqrt[<3>] <8>\cdot \left(\cos \frac<4\pi > <3>+i\cdot \sin \frac<4\pi > <3>\right)=\sqrt[<3>] <8>\cdot (-\frac<1> <2>-\frac <\sqrt<3>> <2>\cdot i)=2\cdot (-\frac<1> <2>-\frac <\sqrt<3>> <2>\cdot i)=-1-\sqrt <3>\cdot i.\]

Готовые работы на аналогичную тему

Вычислим модуль исходного комплексного числа:

Вычислим аргумент исходного комплексного числа:

\[\varphi =\arg z=arctg\frac<1> <1>=arctg1=\frac<\pi > <4>\]

Подставим полученные значения и получим:

Уравнение перепишем в виде:

В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.

\[D=2^ <2>-4\cdot 1\cdot 5=4-20=-16.\]

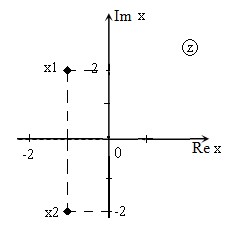
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.

В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.

Запишем уравнение следующим образом:

\[x^ <2>-(1-2i)\cdot x-x\cdot (1+2i)+(1-2i)\cdot (1+2i)=0\] \[x^ <2>-x+2i\cdot x-x-2i\cdot x+1-4i^ <2>=0\] \[x^ <2>-2x+1+4=0\] \[x^ <2>-2x+5=0\]

Рассмотрим квадратное уравнение с комплексными коэффициентами.

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.

В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.

Источник

Квадратное уравнение с комплексными корнями

Всем известно из школы квадратное уравнение:

,

поиск дискриминанта и решение вопроса: имеет ли квадратное уравнение корни или корень или нет. Как следует из основной теоремы алгебры, любое уравнение — ой степени имеет ровно корней с учетом кратности этих корней. Таким образом, любое квадратное уравнение с действительными или комплексными коэффициентами имеет ровно два корня. При этом кратные корни в комплексном анализе считаются ровно столько раз, какая у них кратность.

Утверждение. Пусть коэффициенты многочлена — ой степени

– действительные и его комплексный корень, тогда тоже является корнем этого многочлена.

Получили , следовательно, — также корень многочлена .

Если коэффициенты квадратного трехчлена действительны, а дискриминант отрицательный, то пару сопряженных корней можно найти через дискриминант.

При этом в формуле

нужно учесть что .

Решить квадратное уравнение с действительными коэффициентами: .

Решаем по «половинной» формуле: .

Если квадратный трехчлен имеет хотя бы один не действительный коэффициент, то корни не будут комплексно сопряженными.

Рассмотрим уравнение с комплексными коэффициентами:

Решаем через дискриминант. .

Таким образом, — корни нашего уравнения.

Пример 3

Решить квадратное уравнение:

Опять используем школьную формулу решения. Находим дискриминант:

Чтобы извлечь корень из дискриминанта обратимся к формуле извлечения корня ой степени из комплексного числа. Если , то корни ой степени из имеют вид:

В нашем случае .

Так что корни такие:

Теперь запишем корни исходного квадратного уравнения: .

Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.

Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.

Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.

Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).

В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.

В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.

Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.

Нужна помощь с курсовой или дипломной работой?

Источник

Лекция 4. КОМПЛЕКСНЫЕ ЧИСЛА

Начнем с нескольких напоминаний.

Одна из причин введения рациональных чисел обусловлена требованием, чтобы всякое линейное уравнение ax = b (где a № 0) было разрешимо. В области целых чисел линейное уравнение разрешимо лишь в том случае, когда b делится нацело на a.

Одна из причин расширения множества рациональных чисел до множества действительных чисел была связана с разрешимостью квадратных уравнений, например, уравнения вида x 2 = 2. На множестве рациональных чисел это уравнение не разрешимо, так как среди рациональных нет числа, квадрат которого равен двум. Как известно, – число иррациональное. На множестве же действительных чисел уравнение x 2 = 2 разрешимо, оно имеет два решения x₁ = и x₂ = – .

И все же нельзя считать, что на множестве действительных чисел разрешимы все квадратные уравнения. Например, квадратное уравнение x 2 = – 1 на множестве действительных чисел решений не имеет, так как среди действительных чисел нет такого числа, квадрат которого отрицателен.

Таким образом, действительных чисел явно недостаточно, чтобы построить такую теорию квадратных уравнений, в рамках которой каждое квадратное уравнение было бы разрешимо. Это соображение приводит к необходимости вводить новые числа и расширять множество действительных чисел до множества комплексных чисел, в котором было бы разрешимо любое квадратное уравнение.

Вспомним о едином принципе расширения числовых систем и поступим в соответствии с этим принципом.

Если множество А расширяется до множества В, то должны быть выполнены следующие условия:

1. Множество А есть подмножество В.
2. Отношения элементов множества А (в частности, операции над ними) определяются также и для
элементов множества В; смысл этих отношений для элементов множества А, рассматриваемых уже как элементы множества В, должен совпадать с тем, какой они имели в А до расширения.
3. В множестве В должна выполняться операция, которая в А была невыполнима или не всегда выполнима.
4. Расширение В должно быть минимальным из всех расширений данного множества А, обладающих первыми тремя свойствами, причем это расширение В должно определяться множеством А однозначно (с точностью до изоморфизма).

Итак, расширяя множество действительных чисел до множества новых чисел, названных комплексными, необходимо, чтобы:

а) комплексные числа подчинялись основным свойствам действительных чисел, в частности, коммутативному, ассоциативному и дистрибутивному законам;
б) в новом числовом множестве были разрешимы любые квадратные уравнения.

Множество действительных чисел недостаточно обширно, чтобы в нем были бы разрешимы все квадратные уравнения. Поэтому, расширяя множество действительных чисел до множества комплексных чисел, мы потребуем, чтобы в нем можно было бы построить полную и законченную теорию квадратных уравнений. Другими словами, мы расширим множество действительных чисел до такого множества, в котором можно будет решить любое квадратное уравнение. Так, уравнение x 2 = – 1 не имеет решений во множестве действительных чисел потому, что квадрат действительного числа не может быть отрицательным. В новом числовом множестве оно должно иметь решение. Для этого вводится такой специальный символ i, называемый мнимой единицей, квадрат которого равен – 1.

Ниже будет показано, что введение этого символа позволит осуществить расширение множества действительных чисел, пополнив его мнимыми числами вида bi (где b – действительное число) таким образом, чтобы в новом числовом множестве (множестве комплексных чисел) при сохранении основных законов действительных чисел были разрешимы любые квадратные уравнения.

Основные определения. Операции над комплексными числами

1. Существует элемент i (мнимая единица) такой, что i 2 = – 1.

2. Символ a + bi называют комплексным числом с действительной частью a и мнимой частью bi, где a и b – действительные числа, b – коэффициент мнимой части.

Комплексное число a + 0i отождествляется с действительным числом a, т.е. a + 0i = a, в частности, 0 + 0i = 0. Числа вида bi (b № 0) называют чисто мнимыми.

Например, комплексное число 2 + 3i имеет действительную часть – действительное число 2 и мнимую часть 3i, действительное число 3 – коэффициент мнимой части.

Комплексное число 2 – 3i имеет действительную часть число 2, мнимую часть – 3i, число – 3 – коэффициент при мнимой части.

3. Правило равенства. Два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей.

Т.е., если a + bi = c +di, то a = c, b = d: и, обратно, если a = c, b = d, то a + bi = c +di.

4. Правило сложения и вычитания комплексных чисел.

(a + bi) + (c + di) = (a + c) + (b + d)i.

(2 + 3i) + (5 + i) = (2 + 5) + (3 + 1)i = 7 + 4i;

(– 2 + 3i) + (1 – 8i) = (– 2 + 1) + (3 + (– 8))i = – 1 – 5i;

(– 2 + 3i) + (1 – 3i) = (– 2 + 1) + (3 + (– 3))i =

Вычитание комплексных чисел определяется как операция, обратная сложению, и выполняется по формуле:

(a + bi) – (c + di) = (a – c) + (b – d)i.

(5 – 8i) – (2 + 3i) = (3 – 2) + (– 8 – 3)i = 1 – 11i;

(3 – 2i) – (1 – 2i) = (3 – 1) + ((– 2) – (– 2))i = 2 + 0i = 2.

5. Правило умножения комплексных чисел.

(a + bi)(c + di) = (aс + bd) + (ad + bc)i.

Из определений 4 и 5 следует, что операции сложения, вычитания и умножения над комплексными числами осуществляются так, как будто мы выполняем операции над многочленами, однако с условием, что i 2 = – 1.

Действительно: (a + bi)(c + di) = ac + adi + bdi 2 = (ac – bd) + (ad + bc)i.

Например, (– 1 + 3i)(2 + 5i) = – 2 – 5i + 6i + 15i 2 = – 2 – 5i + 6i – 15 = – 17 + i; (2 + 3i)(2 – 3i) = 4 – 6i + 6i – 9i2 = 4 + 9 = 13.

Из второго примера следует, что результатом сложения, вычитания, произведения двух комплексных чисел может быть число действительное. В частности, при умножении двух комплексных чисел a + bi и a – bi, называемых сопряженными комплексными числами, в результате получается действительное число, равное сумме квадратов действительной части и коэффициента при мнимой части. Действительно:

Произведение двух чисто мнимых чисел – действительное число.

Например: 5i•3i = 15i 2 = – 15; – 2i•3i = – 6i 2 = 6, и вообще bi•di = bdi 2 = – bd.

6. Деление комплексного числа a + bi на комплексное число c + di № 0 определяется как операция обратная умножению и выполняется по формуле:

Формула теряет смысл, если c + di = 0, так как тогда c 2 + d 2 = 0, т. е. деление на нуль и во множестве комплексных чисел исключается.

Обычно деление комплексных чисел выполняют путем умножения делимого и делителя на число, сопряженное делителю.

Опираясь на введенные определения нетрудно проверить, что для комплексных чисел справедливы коммутативный, ассоциативный и дистрибудивный законы. Кроме того, применение операций сложения, умножения, вычитания и деления к двум комплексным числам снова приводит к комплексным числам. Тем самым можно утверждать, что множество комплексных чисел образует поле. При этом, так как комплексное число a + bi при b = 0 отождествляется с действительным числом a = a + 0i, то поле комплексных чисел включает поле действительных чисел в качестве подмножества.

Приведем классификацию комплексных чисел:

Решение квадратных уравнений

Одна из причин введения комплексных чисел состояла в том, чтобы добиться разрешимости любого квадратного уравнения, в частности уравнения

Покажем, что расширив поле действительных чисел до поля комплексных чисел, мы получили поле, в котором каждое квадратное уравнение разрешимо, т.е. имеет решение. Так, уравнение x 2 = – 1 имеет два решения: x₁ = i, x₂ = – i.

Это нетрудно установить проверкой: i•i = i 2 = – 1, (– i)•(– i) = i 2 = – 1.

Перейдем теперь к вопросу о решении полного квадратного уравнения. Квадратным уравнением называют уравнение вида:

ax 2 + bx + c = 0 (a № 0),

где x – неизвестная, a, b, c – действительные числа, соответственно первый, второй коэффициенты и свободный член, причем a № 0. Решим это уравнение, выполнив над ним ряд несложных преобразований.

Теперь можно исследовать полученное решение. Оно зависит от значения подкоренного выражения, называемого дискриминантом квадратного уравнения. Если b 2 – 4ac > 0, то есть действительное число и квадратное уравнение имеет действительные корни. Если же – мнимое число, квадратное уравнение имеет мнимые корни.

Результаты исследования представлены ниже в таблице:

Итак, введение комплексных чисел позволяет разработать полную теорию квадратных уравнений. В поле комплексных чисел разрешимо любое квадратное уравнение.

1. Решите уравнение x 2 – 2x – 8 = 0.

Решение. Найдем дискриминант D = b 2 – 4ac = (– 2) 2 – 4•1•(– 8) = 36 > 0.

Уравнение имеет два действительных корня:

2. Решите уравнение x 2 + 6x + 9 = 0.

Решение. D = 6 2 – 4•1•9 = 0, уравнение имеет два равных действительных корня:

3. Решите уравнение x 2 – 4x + 5 = 0.

Решение. D = 16 – 4•1•5 = – 4

Геометрическая интерпретация комплексных чисел

Известно, что отрицательные числа были введены в связи с решением линейных уравнений с одной переменной. В конкретных задачах отрицательный ответ истолковывался как значение направленной величины (положительные и отрицательные температуры, передвижения в противоположных направлениях, прибыль и долг и т.п.). Однако еще в ХVI веке многие математики не признавали отрицательных чисел. Только с введением координатной прямой и координатной плоскости отчетливо проявился смысл отрицательных чисел, и они стали такими же «равноправными» и понятными, как и натуральные числа. Аналогично обстоит дело с комплексными числами. Смысл их отчетливо проявляется при введении их геометрической интерпретации.

Геометрическая интерпретация комплексных чисел состоит в том, что каждому комплексному числу z = x + yi ставится в соответствие точка (x, y) координатной плоскости таким образом, что действительная часть комплексного числа представляет собой абсциссу, а коэффициент при мнимой части – ординату точки.

Таким образом, устанавливается взаимно однозначное соответствие между множеством комплексных чисел и множеством точек координатной плоскости. Подобным образом было установлено соответствие между множеством действительных чисел и множеством точек числовой прямой.

На рисунке 1 изображена координатная плоскость. Числу 2 + 3i соответствует точка A(2, 3) плоскости; числу 2 – 3i – точка B(2, – 3); числу – 2 + 3i – точка C(– 2, 3); числу – 2 – 3i – точка D(– 2; – 3). Числу 3i соответствует точка E(0, 3); а числу – 3i – точка F(0, – 3). Итак, каждому комплексному числу соответствует единственная точка координатной плоскости и, обратно, каждой точке координатной плоскости соответствует единственное комплексное число, при этом двум различным комплексным числам соответствуют две различные точки координатной плоскости. Ясно, что действительным числам x + 0i соответствуют точки оси абсцисс, а чисто мнимым числам 0 + yi, где y № 0 – точки оси ординат. Поэтому ось Oy называют мнимой, а ось Ox – действительной. Сопряженным комплексным числам соответствуют точки, симметричные относительно оси абсцисс (рис. 2).

Тригонометрическая форма комплексного числа

Точка координатной плоскости, соответствующая комплексному числу z = x + yi, может быть указана по-другому: ее координатами могут быть расстояние r от начала координат и величина угла j между положительной полуосью Ox и лучом Oz (рис. 3).

Расстояние r от начала системы координат до точки, соответствующей комплексному числу z, называют модулем этого числа. Тогда по теореме Пифагора (рис. 2) имеем: r 2 = x 2 + y 2 = (x + yi)(x – yi) = z•z.

Отсюда найдем модуль комплексного числа как арифметическое (неотрицательное) значение корня:

Если комплексное число z изображается точкой оси абсцисс (т.е. является действительным числом), то его модуль совпадает с абсолютным значением. Все комплексные числа, имеющие модуль 1, изображаются точками единичной окружности – окружности с центром в начале системы координат, радиуса 1 (рис. 4).

Угол j между положительной полуосью Ox и лучом Oz называют аргументом комплексного числа z = x + yi (рис. 3).

В отличие от модуля аргумент комплексного числа определяется неоднозначно. Аргумент одного и того же комплексного числа может иметь бесконечно много значений, отличающихся друг от друга на число, кратное 360°. Например, число z (рис. 3) имеет модуль r, аргумент же этого числа может принимать значения j; j + 360°; j + 720°; j + 1080°; … или значения j – 360°; j –720°; j – 1080°; … Данное значение модуля r и любое из приведенных выше значений аргумента определяют одну и ту же точку плоскости, соответствующую числу z.

Пусть точке с координатами (x; y) соответствует комплексное число z = x + yi. Запишем это комплексное число через его модуль и аргумент. Воспользуемся определением тригонометрических функций синуса и косинуса (рис. 3):

Тогда число z выражается через модуль и аргумент следующим образом: z = x + yi = r(cos j + i sin j ).

Выражение z = r(cos j + i sin j ) называют тригонометрической формой комплексного числа, в отличии от выражения z = x + yi, называемого алгебраической формой комплексного числа.

Приведем примеры обращения комплексных чисел из алгебраической формы в тригонометрическую:

Для числа i имеем r = 1, j = 90°, поэтому i = 1(cos 90° + i sin 90°);

Для числа – 1 имеем r = 1, j = 180°, поэтому – 1 = 1(cos 180° + i sin 180°);

Для числа 1 + i имеем поэтому

Для числа имеем r = 1, j = 45°, поэтому

Для числа имеем r = 2, j = 120°, поэтому

Справедливость приведенных равенств нетрудно проверить путем подстановки в их правой части числовых значений тригонометрических функций. Итак, для того, чтобы комплексное число, заданное в алгебраической форме, обратить в тригонометрическую форму, необходимо найти его модуль r и аргумент j, пользуясь формулами:

Комплексные числа и векторы

Таким образом, может быть установлено взаимно однозначное соответствие между множеством точек координатной плоскости (комплексными числами) и множеством векторов, отложенных от начала системы координат.

Если z = x + yi (рис. 5), то вектор , отложенный от начала системы координат до точки, изображающей число z, будет иметь координаты (x; y). Известно, что равные векторы имеют равные координаты.

Итак, мы рассмотрели два способа интерпретации комплексных чисел: их можно изображать либо точками координатной плоскости, либо векторами, отложенными от начала системы координат. При этом любые два равных вектора (имеющих одно и то же направление и равные длины) изображают одно и то же комплексное число, а векторы, отличные либо длиной, либо направлением, изображают разные числа. На рисунке 6 с помощью векторов изображены различные комплексные числа: изображает число 2 + 0i; – число – 3 + 0i; – число 0 + i; – число 0 + 2i; – число 0 – 3i; – число 3 + 2i; – число – 1 – 2i.

Ясно, что любой ненулевой вектор, лежащий на оси Oy (или параллельный ей), изображает чисто мнимое число yi, причем y > 0, если направление вектора совпадает с направлением оси, y

Векторная интерпретация комплексных чисел позволяет уяснить геометрический смысл операций над комплексными числами. Например, сумма двух комплексных чисел 2 + i и 1 + 4i равна 3 + 5i. Каждое из слагаемых изображает соответствующий вектор, отложенный от начала O координат (рис. 7):

= 2 + i; = 1 + 4i.

Для того, чтобы лучше уяснить себе геометрический смысл умножения двух комплексных чисел, воспользуемся их тригонометрической формой. Пусть векторы изображают соответственно комплексные числа:

соответственно модули этих чисел, а j ₁ и j ₂ – их аргументы. Найдем произведение этих чисел:

Воспользуемся известными из школы теоремами сложения синуса и косинуса:

Тогда произведение данных комплексных чисел равно комплексному числу:

Последнее соотношение позволяет сформулировать правило умножения комплексных чисел: при умножении двух комплексных чисел их модули перемножаются, а их аргументы складываются. Это проиллюстрировано на рисунке 8.

Ясно, что произведение комплексных чисел связано с поворотом (вращением). Так, произведение z₁z₂ изображается вектором представляющим собой образ вектора , повернутого на угол j ₂ (или образ вектора , повернутого на угол j ₁), при этом модуль вектора равен произведению модулей данных векторов.

Связь произведения комплексных чисел с вращением становится более наглядной, если рассматривать произведение различных комплексных чисел (векторов) на комплексное число i, у которого модуль равен 1, а аргумент 90°. Например, найдем произведение комплексных чисел z₁ = 1 + i и z₂ = i.

z = z₁z₂ = (1 + i)i = i + i 2 = – 1 + i.

Числа z₁ и z₂ соответственно изображают векторы и (рис.9). Мы видим, что модуль комплексного числа z равен модулю числа z₁:

Источник