что такое метод координат расскажите о нем

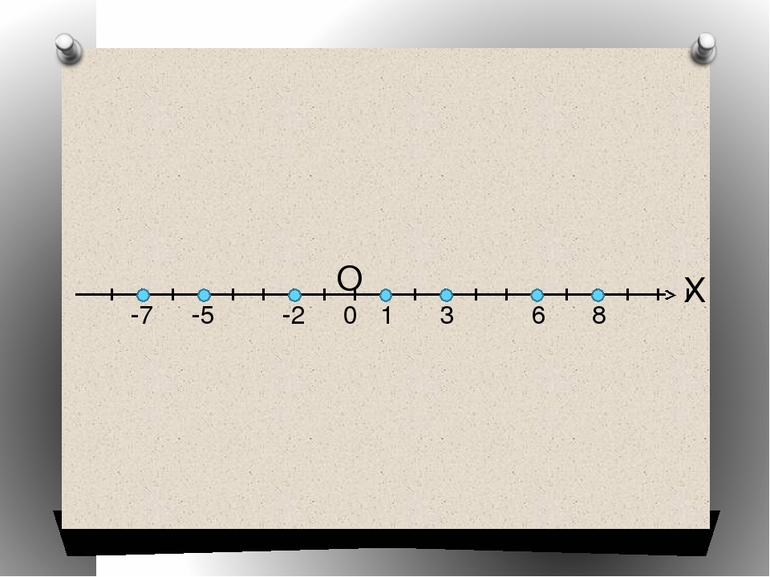
Координаты на прямой

Исследование свойств геометрических тел привело к возникновению отдельной науки — аналитической геометрии. Основополагающим открытием, позволяющим решать задачи, связанные с фигурами, стал координатный метод. В математике принято под координатами понимать положение точки на линии, поверхности или пространстве.

Особенностью способа является нахождение геометрических тел уравнениями. Такой подход позволяет исследовать фигуры и решать задания, взяв за основу алгебраические формулы.

Самая элементарная задача, дающая возможность разобраться в сути, связана с определением положения точки на прямой. Пусть на линии указаны две произвольные точки A и B. Отрезок, который они ограничивают, принимают за единицу длины. Каждой точке P, входящей в AB, соответствует величина, называемая координатой.

Принимать она может три значения:

При выполнении этих условий отрезок называют числовой осью, а A — началом координат. Любая точка, располагающаяся на прямой, имеет свою координату, отличную от других. Но при этом каждое действительное число указывает на расположение точки на рассматриваемой числовой оси. Например, запись вида A (2), B (-¾) обозначает, что числа в скобках являются координатами соответствующих точек.

Расположение на плоскости

Пусть существуют две плоскости, образующие между собой прямой угол. Их точка пересечения A является началом отсчёта любой из них. Если ось одной плоскости обозначить за X, а второй — за Y, то общим для них пространством будет Axy. Ось, совпадающая с X, называется абсциссой, а Y — ординатой. Единица длины для них одинакова. Пересекающиеся оси образуют четверти. Нумерацию принято вести с верхней правой части против часовой стрелки.

Пусть в плоскости Axy находится произвольная точка. Проведя с неё перпендикуляры на оси, получим два пересечения. Числовые значения в этих местах и будут определять положение A на плоскости, то есть её координаты. Записывают их как A (x, y) и называют декартовыми. Таким образом, нахождение A сводится к определению двух точек, лежащих на осях x и y.

Когда точка располагается на оси X, то её ордината имеет нулевое значение, а если Y — абсцисса. В зависимости от того, в какой четверти находится исследуемый объект, определяется знак его координат. В первой оба числа положительные, а в третьей — отрицательные. Во второй же абсцисса имеет положительное значение, а ордината — отрицательное. В третьей же знаки координат обратные второй четверти.

Естественно, что каждой точке на плоскости соответствует пара чисел. Любая фигура состоит из множества точек. Проведя учёт точек и зная их взаимоотношение относительно друг друга, можно изучить свойство объекта. Эти вычисления позволяет выполнить алгебра и арифметика. Поэтому появляется возможность решать геометрические задачи наглядными алгебраическими способами.

В этом и лежит основа использования метода координат в пространстве. Формулы, применяемые при расчётах, хотя и выглядят устрашающе, на самом деле запоминаются легко. Правда, для этого следует выполнить несколько практических заданий.

Скалярное произведение

Пусть есть два вектора a и b с известными координатами (x1, y1) и (x2, y2). Формула для выражения скалярного произведения векторов через координаты будет иметь вид: a* b = x1*x2 + y1*y2. То есть это сумма произведений соответствующих координат.

Для доказательства следует отложить два вектора из одной точки, направленные в разные стороны. Соединив их конечные точки, можно утверждать, что полученный вектор будет равняться разности a и b. Для образованного треугольника выполняется теорема косинусов: AB 2 = OA 2 + OB 2 — 2*OA*OB * cosα. Так как AB — это всё равно, что длина вектора по модулю в квадрате, то вместо AB можно написать вектор, равный a-b.

В итоге получится: |a-b| 2 = |a| 2 + |b| 2 — 2 |a|*|b|*cosα. Последнее перемножение на косинус по определению является скалярным произведением a и b. Выразив его из выражения, справедливо будет записать: a*b = (|a| 2 + |b| 2 — |a — b| 2 ) /2. Подставив координаты в формулу, получим следующее: a*b = (x1 2 + y1 2 + x2 2 + y2 2 — (x1-x2) 2 + (y1-y2) 2 ) /2 = x1*x2 + y1*y2. Равенство доказано.

Основные формулы

Кроме нахождения длины отрезка, к основным формулам относят:

Для понимания формул нужно знать о векторном и смешанном произведении векторов, а также об определителе матрицы. Зная их, можно решать задачи по вычислению элементов простейших многогранников, находить площади и объёмы.

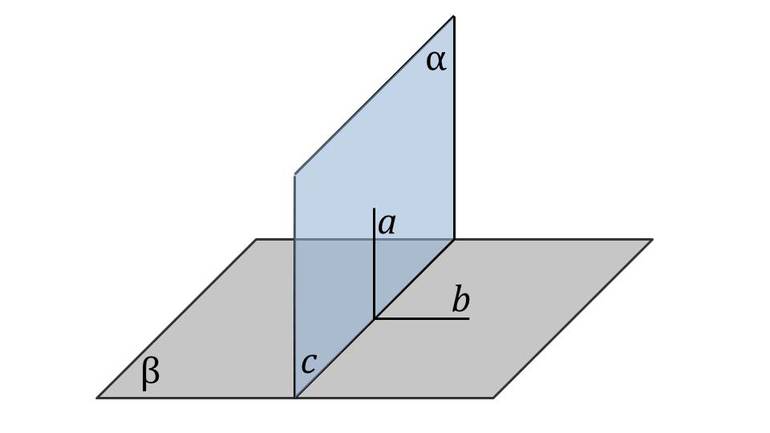
Нахождение угла

Например, необходимо найти угол между плоскостями. Координатным методом решить поставленную задачу несложно. С точки зрения геометрии, это угол между двумя параллелями. Отметив на поверхности начало координат, через него можно провести перпендикуляры обеим плоскостям. Образованный угол и будет искомым. Поэтому для решения задачи необходимо:

Для составления уравнений следует найти положение трёх точек, лежащих в плоскости, но не на одной нормали. Затем каждое из них подставить в уравнение и получить систему. Решается последняя любым доступным методом, например, нахождением определителя матрицы или графическим смешанным методом. В итоге находят корни системы A, B, C и составляют вектор нормали. При этом полученные координаты не должны быть коллинеарными, то есть не лежать на одной прямой или быть параллельными.

Пусть имеется единичный куб, в котором нужно найти угол, образованный A1, B1, C1 и C1, D, A1. Вначале определяют координаты первой плоскости и подставляют их в уравнение: Ax+By+Cz+1 = 0. Тут следует отметить: свободный член добавляется из-за того, что поверхности не проходят через середину координат. Точки определяются значениями: A1 (1, 0, 1), B (0,0,1), D (1,1,0). После подстановки система уравнений примет вид:

Теперь, когда известны N1 и N2, нужно найти косинус между ними, являющийся углом двух искомых плоскостей. Используя формулу для вычисления угла векторов, можно получить следующее: cosα = |½ + ½| / (2 ½ * ¾ ½ ) = 1 / (6 ½ /2) = 2/6 ½ = 6 ½ / 3. Соответственно, угол равен: α = arccos = 6 ½ / 3.

Вычисление площади и высоты

Таким образом, у треугольника две стороны равны, а значит, он равнобедренный. У найденных сторон общей точкой является B (вершина). Следовательно, углы A и C будут равны. Что и требовалось доказать.

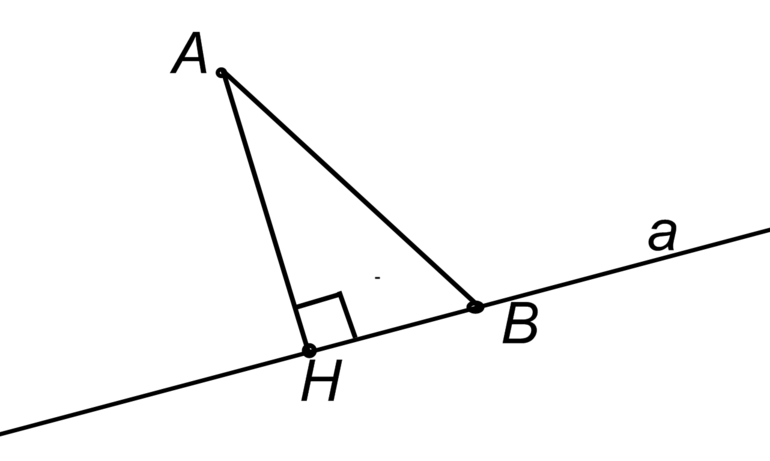
Для того чтобы найти площадь треугольника, используется правило, что она находится умножением высоты на длину стороны, к которой проведена, и делением полученного результата на два: S = h*a/2 = BH * AC /2, где H — точка пересечения высоты и основания.

В равнобедренном треугольнике высота является биссектрисой и медианой, поэтому H лежит на середине отрезка AC. Чтобы найти её положение, используют формулу нахождения координат середины отрезка: H (x, y): X = (-2+4) /2 = 1, Y = (-3+5) / 2 = 1. Искомая точка имеет координаты H (1,1).

Высота находится как корень квадратный из двух точек: BH = ((-3−1) 2 + (4−1) 2 ) ½ = (16+9) ½ = 5. Теперь нужно найти основание треугольника AC. Разницы, из какой координаты вычитать другую, нет, так как результат учитывается по модулю. Основание будет равно: AC = ((-2−4) 2 + (-3−5) 2 ) ½ = (36 + 64) ½ = 10. Полученные значения высоты и основания подставляют в формулу нахождения площади и получают, что она равна: S = 5*10/2 = 25. Задача решена.

Расчёт на онлайн-калькуляторе

Существуют сервисы, позволяющие решать геометрические задачи координатным методом без утомительных самостоятельных вычислений. Сам расчёт обычно занимает не более трёх секунд, а за достоверность результата можно не беспокоиться.

Воспользоваться услугами таких сайтов сможет любой пользователь интернета, даже не имеющий представления о геометрии. Всё, что от него требуется — это подключение к сети и веб-обозреватель с поддержкой Flash-технологии.

Пользователю необходимо ввести условие задания, при этом система будет сама направлять действия и в случае каких-либо ошибок укажет на них, а затем нажать кнопку «Рассчитать». Привлекательность таких сайтов состоит ещё и в том, что ответ будет содержать объяснения с необходимыми формулами и рисунками.

Источник

Метод координат

Метод координат — способ определять положение точки или тела с помощью чисел или других символов (например, положение шахматных фигур на доске определяется с помощью чисел и букв). Числа (символы), определяющие положение точки (тела) на прямой, плоскости, в пространстве, на поверхности и так далее, называются её координатами. В зависимости от целей и характера исследования выбирают различные системы координат.

См. также

Литература

Полезное

Смотреть что такое «Метод координат» в других словарях:

Метод Хука — Дживса (англ. Hooke Jeeves), также как и алгоритм Нелдера Мида, служит для поиска безусловного локального экстремума функции и относится к прямым методам, то есть опирается непосредственно на значения функции. Алгоритм делится на две… … Википедия

Метод главных компонент — (англ. Principal component analysis, PCA) один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих областях,… … Википедия

Метод Главных Компонент — (англ. Principal components analysis, PCA) один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих областях, таких как… … Википедия

метод — метод: Метод косвенного измерения влажности веществ, основанный на зависимости диэлектрической проницаемости этих веществ от их влажности. Источник: РМГ 75 2004: Государственная система обеспечения еди … Словарь-справочник терминов нормативно-технической документации

МЕТОД ИЗОХРОН — математический метод обработки экспериментальных данных, применяемый для установления истинного возраста гр. одновозрастных м лов или г. п. На основании аналитических данных, по содержанию радиоактивных элементов и продуктов их распада полученных … Геологическая энциклопедия

Метод оскулирующих элементов — (Небесная механика) метод качественного анализа траектории возмущённого движения небесного тела. Для улучшения этой статьи желательно?: Дополнить статью (статья слишком короткая либо содержит лишь словарное определение). Найти и… … Википедия

Метод Тёрнера — Метод Тернера классический метод астрофотометрии, предназначен для калибровки координат камеры. Предложен Гербертом Тёрнером в 1893 году.[1] В основу метода положено разложение в ряд функции отображения из небесных координат в… … Википедия

Метод координирования — Метод измерения крена здания (сооружения), при котором вокруг объекта прокладывают замкнутый полигонометрический ход и вычисляют координаты трех или четырех постоянно закрепленных точек, с которых через определенные промежутки времени засечкой… … Словарь-справочник терминов нормативно-технической документации

МЕТОД ВРАЩЕНИЯ КРИСТАЛЛА — способ получения дифракционной картины, возникающей в монокристалле, вращаемом около заданного направления при облучении монохроматическими рентгеновыми лучами. Пленка, на которой фиксируется дифракционная картина, называется рентгенограммой… … Геологическая энциклопедия

Метод Гаусса — Жордана — используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе, отыскания ранга матрицы. Метод является модификацией метода Гаусса. Назван в честь… … Википедия

Источник

Метод координат

«Лучше один раз увидеть, чем сто раз услышать», — гласит народная мудрость. Действительно, рисунки, схемы, чертежи и графики способны заменить нам долгие разъяснения.

Мы с вами рассмотрим прямоугольную систему координат. Её также называют прямоугольной декартовой системой координат — в честь французского математика Рене Декарта.

Нарисуем на листе в клетку две перпендикулярные оси, точку их пересечения обозначим через О.

Горизонтальная ось называется осью ОХ, вертикальная — осью OY. Место пересечения осей ОХ и OY называется началом координат, которое также обозначают цифрой 0 («ноль»). Каждая точка на координатной плоскости имеет свой точный адрес. Это пара чисел: первое число по оси ОХ, второе по оси ОУ. Эти числа называются координатами точки. А чтобы не путать порядок следования координат, вспомните, как устроены наши дома: сначала мы заходим в нужный подъезд (по оси ОХ), а затем поднимаемся на нужный этаж (по оси ОУ).

Посмотрите на шахматную доску. Вдоль её нижнего края идет ряд букв, а вдоль левого — ряд цифр. С их помощью можно однозначно определять положение любой фигуры на шахматной доске.

Оси координат разбивают плоскость на четыре части, которые называются координатными четвертями. Далее мы будем работать только в первой координатной четверти.

Пример. Известны координаты пятнадцати точек:

А(4, 1), В(4, 2), С(1, 2), Д(4, 5), Е(2, 5), F(4, 7), G(3, 7), H(5, 9), I(7, 7), J(6, 7), К(8, 5), L(6, 5), М(9, 2), N(6, 2), 0(6, 1).

Мы провели работу по декодированию графического изображения, состоящего из 15 соединённых отрезками точек, заданных с помощью декартовых прямоугольных координат. Другими словами, мы изменили форму представления информации с числовой на графическую.

Об использовании метода координат в игре Морской бой можно прочитать в § 3.7.

Самое главное

6. Игра «Шифровальщик». Выполните действия по следующему плану:

1) на листочке в клетку нарисуйте произвольный многоугольник;
2) пронумеруйте его вершины и закодируйте их с помощью координат:
3) задайте порядок соединения вершин;
1) проверьте, не допущена ли вами ошибка при кодировании рисунка;
5) координаты точек и порядок их соединения выпишите на отдельный листок;
6) предложите кому-нибудь восстановить ваш рисунок по этому коду;
7) сравните результаты — возможно искажение информации при декодировании.

Босова Л. Л., Информатика и ИКТ : учебник для 5 класса Л. Л. Босова. М. : БИНОМ. Лаборатория знаний, 2009. 192 с. : ил.

Источник

Класс: 9

Презентация к уроку

Профиль класса: физико-математический

Тип урока – повторительно-обобщающий, 45 мин.

Ход урока

1.1. Взаимное приветствие учителя и учащихся

1.2. Сообщение темы и цели урока.

1.3. Настрой на урок.

Цель: Выяснить у ответственных учеников о готовности учащихся к уроку.

II. Проверка домашнего задания: №902; №1000а; №1044а; 1041а.

3 мин.№900. Дано: ABC, A(4;8), B(12;11), C(7;0)

Доказать: ABC – равнобедренный, но не равносторонний.

1) d=

AB=

2) AC=

3) BC=

Так как AB=AC, то ABC – равнобедренный с основанием BC.

Ответ: ABC– равнобедренный с основанием BC.

№1000.

Выяснить: Является ли это уравнение уравнением окружности, если “да”, то найти координаты центра и радиус окружности.

Ответ: R=5; (1;-2) – координаты центра данной окружности.

№1041.

Дано: , ,

Найти:

=

=

Ответ:

№1044(а).

Дано:

Найти:

x₁x₂+y₁y₂

а) “Из истории возникновения и развития метода координат”. Приготовил: Патрашкин Егор.

Первоначально идея координат зародилась в древности в связи с потребностями астрономии, географии, живописи. Так, на стене одной из древнеегипетских погребальных камер была обнаружена квадратная сетка (палетка), которой пользовались для увеличения изображений

Древнегреческий астроном Клавдий Птолимей применил географические координаты для определения местонахождения мореплавателя. Идеей координат пользовались в середине века для определения положения светил на небе, для определения места на поверхности Земли. Прямоугольной сеткой пользовались художники эпохи Возрождения.

Применять координаты в математике впервые стали Ферма и Декарт. В 1637 году вышла книга Декарта Рассуждения о методе, в которой наряду с общими философскими рассуждениями о материи значительное место уделяется универсальной математике.

Заслуга Декарта состояла в том, что он ввел переменные координаты.

Так, в уравнении ах + ву = с,

буквы х и у стали рассматриваться не как неизвестные, а как переменные.

Метод координат позволяет строить графики уравнений, изображать геометрически различные зависимости, выраженные аналитически с помощью уравнений и формул, решать различные геометрические задачи с помощью алгебры. Термины абсцисса, ордината были введены в употребление Г. Лейбницем в 70, 80-е годы XVII в.

Выполнил Путрин Антон:

Дан треугольник ABC, где M – середина отрезка AB. Найти координаты M, если A(3;5), а B(3;8).

Источник

Класс: 5

Презентация к уроку

Класс: 5 класс. Программа «Школа 2100» ФГОС.

Тип урока: Урок освоения новых знаний и способов действий.

Цель урока: Способствовать формированию у обучающихся навыков кодирования графической информации с помощью метода координат.

Решаемые учебные задачи:

Методы: Репродуктивный, словесный, наглядный.

Методические приемы: Анализ задач, эвристическая беседа

Оборудование: Компьютеры; Мультимедийный проектор и экран.

План урока:

Планируемые результаты

Ход урока

Создать благоприятный психологический настрой на работу

Приветствие. Проверка готовности учащихся к уроку

Садятся согласно ряду и месту, указанному на билете.

Эмоционально настраиваются на работу, включаются в деловой ритм урока

Личностные: психологическая готов-ность учащихся к уроку, создание благоприятного микроклимата

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками

Слайд 1

– Что такое кодирование?

– Какие виды информации вы знаете?

– Какой вид информации мы кодировали на прошлом уроке?

Молодцы! Все эти понятия мы прошли с вами на предыдущих уроках.

В виде чисел на слайде закодирована текстовая информация, связанная с темой нашего сегодняшнего урока.

Четко и быстро отвечают на вопросы и выполняют задание

Личностные: самоопределение

Регулятивные: целеполагание, взаимокон-троль, коррекция, самооценка качества усвоения материала

Познавательные: формирование представ-ления об основных изучаемых понятиях: кодирование, метод координат, координатная плоскость. Умение соотносить определения и термины

Коммуникативные: постановка вопросов, умение слушать собеседника

Актуализация опорных знаний и способов действий.

Слайд 2

– Что мы с вами сейчас сделали?

– Какой способ кодирование здесь был применен?

– Какой вид информации мы будем кодировать сегодня?

– Так что же будет являться целью нашего урока?

Декодируют словосочетание «Метод координат»

Кодирование графической информации с помощью метода координат

Обеспечение мотивации учения детьми, принятие ими целей урока.

Слайд 3

На уроках математики вы уже сталкивались с простым видом системы координат — числовой осью. Но сегодня мы познакомимся с декартовой системой координат.

Слайд 4

Идет обсуждение сообщения, задаются вопросы.

Обучающиеся смотрят на слайд

Один ребенок читает сообщение о Рене Декарте. Остальные слушают. Общаются, отвечают на вопросы.

Регулятивные: принимать учебную задачу и следовать инструкции учителя

Коммуникативные: умение слышать и слушать

Создание проблемной ситуации. Спрогнозировать предстоящую деятельность

Слайд 5

Давайте посмотри как же выглядит декартовая (прямоугольная) система координат.

– Что вы можете сказать про ось X? Про ось Y?

– На сколько частей делится плоскость?

Правильно, молодцы, это 4 четверти, мы с вами будем работать с первой частью, где используются положительные числа.

– Если я поставлю точку на плоскости, то как я смогу ее закодировать?

Учащиеся отвечают на вопросы, идет обсуждение

Пересечение двух прямых.

Х – горизонтальная, Y – вертикальная.

Дети выдвигают свои версии, идет обсуждение.

Личностные: Способность к избирательному отношению к получаемой информации за счет умений ее анализа и критичного оценивания;

Познавательные: самостоятельное решение проблем творческого и поискового характер

Коммуникативные: умение слышать и слушать

Изучение нового материала

Слайд 6

Для кодирования точки есть определенное правило. В скобках записывается через запятую два числа, первое по оси X, второе по оси Y. Запомнить это правило мне помогла такая схема. Представьте, что вы возвращаетесь из школы домой. Вы живете во втором подъезде на втором этаже.

– Вдоль какой оси вы вначале пойдете?

– На второй этаж вдоль какой оси будете подниматься?

Обучающиеся слушают и отвечают на вопросы.

Познавательные: осуществляют поиск и выделение необходимой информации.

Регулятивные: принимать учебную задачу и следовать инструкции учителя

Коммуникативные: умение слышать и слушать

Умение выделять главное, существенное, логически излагать свои мысли

Слайд 7-8

Давайте теперь потренируемся определять координаты.

Слайд 9

А теперь, наоборот, по заданным координатам построим изображение.

Слайд 10-11

В рабочих тетрадках выполните задание № 99 на странице 69.

Сравните получены результат с изображением на слайде. Те, кто быстро делает работу получают дополнительно задание.

Слайд 12

Обучающиеся определяют координаты геометрических фигур

В тетрадях рисуют систему координат и строят изображение

обучающиеся выполняют физкультминутку

Личностные: Способность к избирательному отношению к получаемой информации за счет умений ее анализа и критичного оценивания;

Регулятивные: принимать учебную задачу и следовать инструкции учителя

Познавательные осуществляют поиск и выделение необходимой информации.

Тренировать навыки работы с «Координатной плоскостью»

Совместно с учащимися рассматриваем интерфейс новой программы, знакомимся с ее возможностями.

Раздаю карточки с заданием. Тот, кто быстро работает, получает карточку с дополнительным заданием или помогает отстающим.

Слайд 13-15

Проверяем полученные результаты.

Слайд 16

Пересаживаемся за парты. Проводится игра.

На координатной плоскости расположены разноцветные точки, определите их координаты.

Проверяем полученные результаты.

Пересаживаются за компьютеры, запускают программу «Координатная плоскость»

Определяют координаты точек

Личностные: готовность к повышению своего образовательного уровня и продолжению обучения с использованием средств ИКТ (компьютера);

Коммуникативные: умение слушать, вести диалог;

Регулятивные: принимать учебную задачу и следовать инструкции учителя; достижения цели при помощи фиксированного набора средств

Познавательные: Выполнение задания в программе «Координатная плоскость»

Дать качественную оценку работы класса и отдельных учеников

Слайд 17-18

Сегодня вы заходили в кабинет по билетам. Как вы думаете, какой способ кодирования при этом использовался?

Слайд 19-20

Приведите примеры, где еще в быту используется метод координат?

Слайд 21 Домашнее задание

Придумать и нарисовать рисунок в тетради, и написать к нему программу.

Закрепить, повторить полученные знания по темам «Кодирование информации». «Метод координат»

обучающиеся записывают домашнее задание

Личностные: самоорганизация

Регулятивные: Оценка и осознание уровня и качества усвоения; контроль

Коммуникативные умение выражать мысли, слушать, вести диалог

Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе.

Как вы считаете, все ли вам удалось выполнить, сделать за сегодняшний урок? Если нет то, какие трудности возникли при выполнении заданий?

обучающиеся отвечают, выражая собственное мнение

обучающиеся дописывают на листочках фразы

Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли;

Познавательные: рефлексия.

Источник

• ← что такое преддиабет симптомы у женщин
• ликер трипл сек что это →