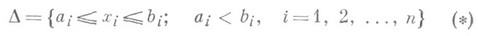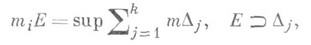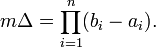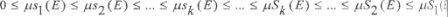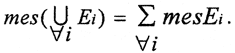что такое мера жордана

ЖОРДАНА МЕРА

в R n объем этого параллелепипеда.

Для ограниченного множества определяются: внешняя мера Жордана

и внутренняя мера Жордана

где В этом случае Ж. м. равна mE=m_eE=m_iE.

Ограниченное множество измеримо по Жордану тогда и только тогда, когда его граница имеет Ж. м. нуль (или, что равносильно, когда его граница имеет Лебега меру нуль).

Приведенное понятие меры ввели Дж. Пеано [1] и К. Жордан [2]. Внешняя Ж. м. одна и та же для Еи Е( замыкания множества Е )и равна Бореля мере Е. Измеримые по Жордану множества образуют кольцо множеств, на к-ром Ж. м. конечно аддитивная функция. См. также Квадрируемость.

Лит.:[1] Реanо G., Applicazioni geometriche del calcolo infinitesimale, Torino, 1887; [2] Jordan C, «J. math, pures et appl.», 1892, t. 8, p. 69-99; [3] Никольский С. М., Курс математического анализа, т. 2, М., 1973; [4] Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 4 изд., М., 1976.

Полезное

Смотреть что такое «ЖОРДАНА МЕРА» в других словарях:

Мера Жордана — Мера Жордана один из способов формализации понятия длины, площади и мерного объёма в мерном евклидовом пространстве. Содержание 1 Построение 2 Свойства … Википедия

МЕРА — множества, обобщение понятия длины отрезка, площади фигуры, объема тела, интуитивно соответствующее массе множества при нек ром распределении массы по пространству. Понятие М. множества возникло в теории функций действительного переменного в… … Математическая энциклопедия

Мера Лебега — на мера, являющаяся продолжением меры Жордана на более широкий класс множеств, была введена Лебегом в 1902 году. Содержание 1 Построение меры на прямой 1.1 … Википедия

Мера — в Викисловаре? … Википедия

Мера вероятности — Мера качественная и/или количественная пропорция соотношения истин. Во многом пропорция устанавливается произвольно. Термины Мера (в метрологии) синоним единицы измерения. Мера внесистемная русская единица объёма. Мера (философия) философский… … Википедия

Мера множества — У этого термина существуют и другие значения, см. Мера. Мера множества неотрицательная величина, интуитивно интерпретируемая как размер (объем) множества. Собственно, мера это некоторая числовая функция, ставящая в соответствие каждому… … Википедия

Жорданова мера — Мера Жордана один из способов формализации понятия длины, площади и n мерного обьёма в n мерном евклидовом пространстве. Содержание 1 Построение 2 Свойства 3 История … Википедия

Конечно-аддитивная мера — Мера общее название различных типов обобщений понятий евклидовой длины, площади и n мерного объёма для более общих пространств. Если обратное не указано явно, то обычно подразумевается счётно аддитивная мера. Содержание 1 Определения 1.1 Конечно … Википедия

Конечно аддитивная мера — Мера общее название различных типов обобщений понятий евклидовой длины, площади и n мерного объёма для более общих пространств. Если обратное не указано явно, то обычно подразумевается счётно аддитивная мера. Содержание 1 Определения 1.1 Конечно … Википедия

Разложение Хана-Жордана — Заряд вещественнозначная конечно аддитивная функция множества, определённая на некоторой σ алгебре, (например, борелевских подмножеств). В отличие от обычной меры под которой, обычно понимают положительную σ аддитивную функцию множества, заряд… … Википедия

Источник

Жорданова мера

Содержание

Построение

Мера Жордана mΔ параллелепипеда 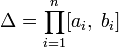в определяется как произведение

Для ограниченного множества 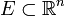определяются:

здесь 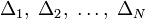— параллелепипеды описанного выше вида.

Свойства

История

Приведённое понятие меры ввели Пеано (1887) и Жордан (1892). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.

Литература

См. также

Полезное

Смотреть что такое «Жорданова мера» в других словарях:

СПЕКТРАЛЬНАЯ МЕРА — унитальный гомоморфизм нек рой булевой алгебры множеств в булеву алгебру проекторов в банаховом пространстве. Всякий оператор Тв банаховом пространстве Xопределяет С. м. на совокупности открыто замкнутых подмножеств его спектра по формуле где Г… … Математическая энциклопедия

Жордан, Мари Энмон Камиль — Мари Энмон Камиль (Камилл) Жордан Marie Ennemond Camille Jordan Дата рождения … Википедия

ДВУХ КОНСТАНТ ТЕОРЕМА — пусть D конечносвязная жорданова область на плоскости комплексного переменного z, w(z) регулярная аналитич. функция в D, удовлетворяющая неравенству причем на нек рой дуге a. границы дD выполняется соотношение тогда в каждой точке z множества где … Математическая энциклопедия

КВАДРИРУЕМОСТЬ — измеримость по Жордану множества на плоскости (см. Жордана мера). Не всякая область (т. е. открытое связное множество) и даже но всякая жорданова область (т. е. область, имеющая своей границей простую замкнутую кривую) квадрируема. С другой… … Математическая энциклопедия

ПЛАТО ЗАДАЧА — задача нахождения минимальной поверхности (м. п.) с заранее заданной границей Г. Впервые такая задача была поставлена Ж. Лагранжем (J. Lagrange, 1760), к рый свел ее в классе поверхностей вида z=z( х, у).к решению уравнения Эйлера Лагранжа м. п.… … Математическая энциклопедия

Жордан Мари Энмон Камиль — Камиль Жордан Мари Энмон Камиль (Камилл) Жордан (фр. Marie Ennemond Camille Jordan, 5 января 1838 22 января 1922) французский математик, известный благодаря своим фундаментальным работам в теории групп и «Курсу анализа». Он родился в Лионе и… … Википедия

Камилл Жордан — Камиль Жордан Мари Энмон Камиль (Камилл) Жордан (фр. Marie Ennemond Camille Jordan, 5 января 1838 22 января 1922) французский математик, известный благодаря своим фундаментальным работам в теории групп и «Курсу анализа». Он родился в Лионе и… … Википедия

Мари Энмон Камиль Жордан — Камиль Жордан Мари Энмон Камиль (Камилл) Жордан (фр. Marie Ennemond Camille Jordan, 5 января 1838 22 января 1922) французский математик, известный благодаря своим фундаментальным работам в теории групп и «Курсу анализа». Он родился в Лионе и… … Википедия

Источник

Понятие объема в n-мерном пространстве (мера Жордана). Измеримые множества

Понятие объема в n-мерном пространстве (мера Жордана). Измеримые множества

Понятие объема в n-мерном пространстве (мера Жордана). Измеримые множества. кратко напомним основные понятия, связанные с определением n-мерного объема (площади в случае n = 2), и дадим новое определение. Разделение понятия на заданный объем (меру).Это отличается от того, что было введено ранее (см. раздел 31.1). HN в N-мерном евклидовом пространстве (n = 1, 2,3,…И чтобы. Эта точка, как обычно, x-(x1,…хп).Где XI, 1 = 1,2,…n-это Координата точки x в фиксированной системе координат. Неотрицательное целое число k(k = 0, 1,…Исправить это.)Первая координатная ось ((=1, 2,…, n), то есть координаты X!= …х ^ р-x1n = … Рассмотрим множество точек x с = X / r =0. х,= 1 () РМ, М-0、±1、±2、…Через эту точку с координатами в виде Гиперплоскость размерности η-1, ортогональная этой оси.

Кроме того, множество лежит находится в многограннике»строго внутри», то есть оно не пересекается. Людмила Фирмаль

Объем его Р-размерности определяется уравнением 11 (44.2)） В Очевидно, что p5-неотрицательное число или+ oo. Здесь пусть это произвольное множество% N. 5 * = 5k(E) представляет собой множество точек всех X-мерных кубов ранга k, которые все находятся в E, а 3k = 3k (E) представляет собой множество точек всех X-мерных кубов ранга k, которые пересекают множество E, соответственно…） 8К(Е)= Г Эл、 ？л = я 8К (Е)= Г 2А, рН Людмила Фирмаль

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Математическая энциклопедия

Смотреть значение Жордана Мера в других словарях

Мера — меры, ж. 1. Единица измерения протяжения или емкости. длины. веса. Меры сыпучих тел. Кубические меры. 2. Предел, граница, размер. Чудится, будто. голубая зеркальная дорога.
Толковый словарь Ушакова

Мера — Действие, направленное для достижения чего-либо; наказание (обычно во мн. числе).
Активная, безотлагательная, благоразумная, вынужденная, высшая, действенная, демократическая.
Словарь эпитетов

Мера Ж. — 1. Единица измерения. 2. Старинная русская единица емкости для сыпучих тел, равная приблизительно одному пуду зерна. // Сосуд для измерения сыпучих тел, вмещающий такое.
Толковый словарь Ефремовой

Мера Наказания — наказание, назначаемое судом подсудимому на основании нормы уголовного права.
Экономический словарь

Мера Потребления — мера, доля национального дохода, которую должен получить каждый работающий член общества, в соответствии с затраченным трудом.
Экономический словарь

Мера Предосторожности — действие, предпринимаемое для ограждения интересов страхователя или предотвращения нежелательных рисков.
Экономический словарь

Мера Пресечения — метод пресечения попыток подозреваемого уклониться от явки в
органы дознания, в суд, помешать установлению истины или продолжить преступную деятельность. В качестве.
Экономический словарь

Мера Рентабельности (profit Margin) — Соотношение прибыли и выручки.
Прибыль может как включать, так и не включать экстраординарные события и показываться в
размере как до, так и после уплаты налогов.
Экономический словарь

Мера Торговая — установленное биржей минимальное количество ценных бумаг, образующих одну партию.
Экономический словарь

Мера Труда — мера участия каждого работника в совокупном общественном труде.
Экономический словарь

Часть, Доля, Мера, Единица — В общем значении: единица измерения. Любая часть Количества, принимаемая в качестве стандарта измерений или обмена. Например, на рынке товарно-сырьевой продукции единицей.
Экономический словарь

Мера — Общеславянское слово, образованное от индоевропейской основы те. В древнеиндийском находим mati – «мерит», в латинском – metior («мерю, измеряю»). Родственные слова: метр, английское measure («мера»).
Этимологический словарь Крылова

Мера — в России емкость для измерения жидких и сыпучих тел. Обычно равначетверику (26,24 л).
Большой энциклопедический словарь

Мера Пресечения — в уголовном процессе способ пресечения попытокобвиняемого уклониться от явки в следственные органы и в суд, помешатьустановлению истины или продолжить преступную.
Большой энциклопедический словарь

Мера — — в России емкость для измерения жидких и сыпучих тел, обычно равна четверику — 26,24 п.
Исторический словарь

Мера — Русская мера вместимости жидкостей и сыпучих тел, равная четверику = 26,24 л.
Словарь мер и весов

Мера Различий — основных тенденций социальных групп отражает различия степени или уровня влияния, оказываемого независимой переменной.
Социологический словарь

Источник

Что такое мера жордана

2.2. Понятие меры

Понятие меры есть естественное обобщение понятий длины, площади, объёма и их приложений.

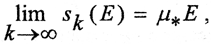
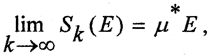
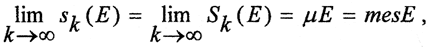
Последовательность <μs_k(E)> не убывает и ограничена сверху, а последовательность <μS_k(E)> не возрастает и ограничена снизу. Поэтому эти последовательности имеют пределы и которые называются соответственно внутренней и внешней мерой Жордана множества E. Если они совпадают, то есть то mesE называется мерой Жордана множества E, а фигура E называется измеримой (квадрируемой).

Аналогично строится мера Жордана для множества E⊂R n и для множества E⊂R. Длина, площадь, объём обладают естественными свойствами, которые, как всегда, примем за аксиомы.

Определение 1. Под мерой будем понимать функцию, заданную на множестве всех измеримых фигур, обладающую следующими свойствами:

2. Мера суммы конечной или счётной системы попарно непересекающихся множеств равна сумме их мер:

3. При перемещении множества как твёрдого тела его мера не меняется.

4. Мера единичного квадрата(отрезка, куба) равна единице.

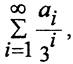
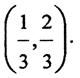
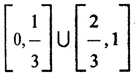
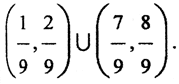
( Комментарий. Пример измеримого, но очень специфического множества даёт канторов дисконтинуум. Это подмножество отрезка [0,1] числовой оси, состоящее из всех чисел вида где a_i равно 0 или 2, которое получается следующим образом. Отрезок [0,1] делится на три части и затем выбрасывается средняя часть Оставшиеся отрезки вновь делим на три части и выбрасываем средние части И так далее. Это называют процедурой Кантора.

Ясно, что множество тех сегментов, которые целиком содержатся в канторовом дисконтинууме, пусто. Множество же тех сегментов, каждый из которых пересекается с отрезком [0,1] образует последовательность 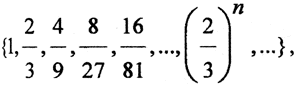которая стремится к нулю. Таким образом, мера Жордана канторова дисконтинуума равна нулю.

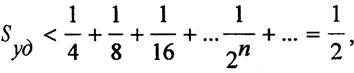
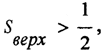
Не все множества измеримы по Жордану. Опять применим процедуру Кантора к отрезку [0,1] и удалим из него интервал с длиной, меньшей, чем 1 /₄. Затем из каждого из получившихся двух сегментов удалим интервалы с общей длиной, меньшей, чем 1 /₈, и так далее. В результате общая длина удалённых частей то есть то, что осталось, имеет длину тогда как фигура не содержит никакого отрезка. Это значит, что S_нижн. = 0. Стало быть, фигура неизмерима по Жордану.

Ещё один важный пример. Рассмотрим множество рациональных чисел сегмента [0,1]. Это множество плотно на сегменте [0,1]. То есть между любыми двумя точками сегмента [0,1] найдутся как рациональные числа, так и иррациональные. Разделим сегмент [0,1] на две части, затем на четыре части и т. д. Множество тех сегментов, которые целиком содержатся во множестве рациональных чисел, пусто, и его мера равна нулю. Множество же тех сегментов, каждый из которых пересекается с отрезком [0,1], просто состоит из этих сегментов, то есть их объединение и составляет отрезок [0,1], мера которого по определению равна единице. То есть множество рациональных чисел неизмеримо по Жордану. Абсолютно такие же рассуждения приводят к тому, что множество иррациональных чисел тоже неизмеримо по Жордану. Получается, что отрезок [0,1], мера которого равна единице, состоит из неизмеримых множеств.

Источник