что такое материальное моделирование
Идеальные и материальные модели
Неоднозначность термина «модель», огромное число типов моделирования и их быстрое развитие затрудняют в настоящее время построение логически законченной, удовлетворяющей всех классификации моделей. Любая подобная классификация условна в силу того, что она отражает, с одной стороны, субъективную точку зрения авторов, а с другой — ограниченность их знаний в конечном числе областей научного познания.
Данную классификацию следует рассматривать как попытку построения некоторого инструмента или модели для исследования свойств и характеристик самого процесса моделирования. Моделирование относится к общенаучным методам познания. Использование моделирования на эмпирическом и теоретическом уровнях исследования приводит к условному делению моделей на материальные и идеальные.
Материальное моделирование — это моделирование, при котором исследование объекта выполняется с использованием его материального аналога, воспроизводящего основные физические, геометрические, динамические и функциональные характеристики данного объекта. Основными разновидностями материального моделирования являются натурное и аналоговое. При этом оба вида моделирования основаны на свойствах геометрического или физического подобия.
Идеальное моделирование отличается от материального тем, что оно основано не на материализованной аналогии объекта и модели, а на аналогии идеальной, мыслимой и всегда носит теоретический характер. Идеальное моделирование является первичным по отношению к материальному. Вначале в сознании человека формируется идеальная модель, а затем на ее основе строится материальная.
Материальное моделирование
Основными разновидностями материального моделирования являются натурное и аналоговое. При этом оба вида моделирования основаны на свойствах геометрического или физического подобия. Две геометрические фигуры подобны, если отношение всех соответственных длин и углов одинаковы. Если известен коэффициент подобия — масштаб, то простым умножением размеров одной фигуры на величину масштаба определяются размеры другой, ей подобной геометрической фигуры. Два явления физически подобны, если по заданным характеристикам одного можно получить характеристики другого простым пересчетом, который аналогичен переходу от одной системы единиц измерения к другой. Изучением условий подобия явлений занимается теория подобия.
Натурное моделирование — это такое моделирование, при котором реальному объекту ставится в соответствие его увеличенный или уменьшенный материальный аналог, допускающий исследование (как правило, в лабораторных условиях) с помощью последующего перенесения свойств изучаемых процессов и явлений с модели на объект на основе теории подобия.
Аналоговое моделирование — это моделирование, основанное на аналогии процессов и явлений, имеющих различную физическую природу, но одинаково описываемых формально (одними и теми же математическими соотношениями, логическими и структурными схемами). В основу аналогового моделирования положено совпадение математических описаний различных объектов.
Модели физического и аналогового типов являются материальным отражением реального объекта и тесно связаны с ним своими геометрическими, физическими и прочими характеристиками. Фактически процесс исследования моделей данного типа сводится к проведению ряда натурных экспериментов, где вместо реального объекта используется его физическая или аналоговая модель.
Идеальное моделирование
Идеальное моделирование разделяют на два основных типа: интуитивное и научное.
Интуитивное моделирование — это моделирование, основанное на интуитивном (не обоснованном с позиций формальной логики) представлении об объекте исследования, не поддающимся формализации или не нуждающимся в ней. В качестве наиболее яркого примера интуитивной модели окружающего мира можно считать жизненный опыт любого человека. Любое эмпирическое знание без объяснения причин и механизмов наблюдаемого явления также следует считать интуитивным.
Научное моделирование — это всегда логически обоснованное моделирование, использующее минимальное число предположений, принятых в качестве гипотез на основании наблюдений за объектом моделирования.
Главное отличие научного моделирования от интуитивного заключается не только в умении выполнять необходимые операции и действия по собственно моделированию, но и в знании «внутренних» механизмов, которые используются при этом. Можно сказать, что научное моделирование знает не только, как необходимо моделировать, но и почему так нужно делать. Необходимо подчеркнуть чрезвычайно важную роль интуиции, интуитивных моделей в науке, без них не обходится не одно сколь-нибудь новое знание. Последнее недостижимо только методами формальной логики.
Интуитивное и научное (теоретическое) моделирование ни в коей мере нельзя противопоставлять одно другому. Они хорошо дополняют друг друга, разделяя области своего применения.
Знаковым называют моделирование, использующее в качестве моделей знаковые изображения какого-либо вида: схемы, графики, чертежи, наборы символов, включающее также совокупность законов и правил, по которым можно оперировать с выбранными знаковыми образованиями и элементами. В качестве примеров таких моделей можно назвать любой язык, например: устного и письменного человеческого общения, алгоритмический и т.д. Знаковая форма используется для передачи как научного, так и интуитивного знания. Моделирование с помощью математических соотношений также является примером знакового моделирования.
Интуитивное знание является генератором нового знания. Однако далеко не все догадки и идеи выдерживают последующую проверку экспериментом и методами формальной логики, свойственными научному подходу, выступающему в виде своеобразного фильтра для выделения наиболее ценных знаний.
Материальное моделирование
Материальные модели характерны тем, что они более наглядны и просты для понимания. В самом деле, все модели этого класса основаны на использовании свойства подобия между ними и какими–либо объектами–оригиналами. При этом физические модели обычно являются геометрически подобными оригиналам, а аналоговые – напротив, физически. Допустим, макет торпеды должен обладать геометрическим подобием, а процесс обтекания его потоками жидкости и газа или колебаний в этих средах – описываться одними и теми же математическими соотношениями.
Методы физического(натурного, предметного) моделирования нашли самое широкое применение в авиа–, автомобиле–, ракето– и судостроении, а также в других отраслях промышленности и транспорта. Например, при разработке нового летательного аппарата большое значение имеют эксперименты с натурными образцами или моделями в аэродинамической трубе. Исследование полученных там результатов их обтекания воздушным потоком позволяет найти наиболее рациональные формы корпуса самолета либо ракеты и всех их выступающих частей.
В основу аналоговогомоделирования положено совпадение (преимущественно – качественное) математического описания различных предметов, процессов и явлений. Характерным примером аналоговых моделей служат механические и электрические колебания, которые подчинены одним и тем же законам, т.е. описываются одинаковыми аналитическими формулами, но относятся к качественно различным физическим процессам.
При некоторых допущениях аналогичными можно считать большинство процессов, протекающих в газе и жидкости, включая обтекание их потоками различных тел, а также явления теплопереноса и диффузии примесей. Основное удобство аналоговых моделей заключается в том, что изучение одних процессов можно проводить в других, более удобных условиях. Например, изучение тех же механических колебаний можно вести с помощью электрической схемы, а обтекание жидкости заменить обтеканием газом, и наоборот.
Идеальное моделирование
Что касается правой части схемы классификации методов моделирования, включающей в себя идеальные (воображаемые) модели и методы их использования, то здесь ситуация значительно сложнее. Как по их количеству и строгости деления по классам, так и по однозначности восприятия и интерпретации конкретных моделей.
Под интуитивным(иногда называемым также «ненаучным») обычно подразумевают моделирование, использующее не обоснованное с позиций формальной логики представление объекта исследования, которое к тому же не поддается формализации или не нуждается в ней. Такое моделирование осуществляется в сознании человека, в форме мысленных экспериментов, сценариев и игровых ситуаций с целью его подготовки к предстоящим практическим действиям.
Естественно, что основой для подобных моделей служит жизненный опыт людей, т. е. знания и умения, накопленные каждым человеком и передающиеся от поколения к поколению. Кроме того, любое эмпирическое знание, полученное людьми из эксперимента или в процессе наблюдения без объяснения причин и механизмов наблюдаемых явлений, также можно считать интуитивным и использовать при соответствующем моделировании.
В отличие от интуитивного семантическое(смысловое) моделирование логически обосновано с помощью некоторого числа исходных предположений. Сами эти предположения нередко принимают форму гипотез, создаваемых на основе наблюдения за объектом моделирования или какими–либо его аналогами. Главное отличие этого вида моделирования от предыдущего заключается не только в умении выполнять и воспроизводить для других его действия, но и в знании внутренних механизмов, которые используются при этом.
В группу семантических методов входит вербальное (словесное) и графическое моделирование. При этом первый тип моделей образуется с помощью слов, из которых составляются высказывания, суждения и умозаключения относительно моделируемого объекта. А при графическом моделировании уже используются материальные носители информации – бумага, классная доска или монитор компьютера, на которых размещаются различные рисунки, чертежи, структурно–функциональные схемы или диаграммы причинно–следственных связей.
В отличие от смыслового семиотическое, или знаковое, моделирование является наиболее формализованным, поскольку использует не только общеизвестные слова или довольно наглядные изображения (как в семантических моделях), но и разного рода символы – буквы, иероглифы, нотные знаки, цифры. Более того, в последующем все они объединяются с помощью специфических правил, по которым принято оперировать как отдельными элементами, так и создаваемыми из них знаковыми образованиями.
Основным подвидом данного моделирования считается математическое моделирование. Далее под математическиммоделированием будет подразумеваться идеальное знаковое формальное моделирование, при котором описание объекта–оригинала осуществляется на языке математики, а исследование модели проводится с использованием тех или иных математических методов [23]. Использование математического языка предопределяет необходимость все операции и преобразования в математических моделях осуществлять над математическими объектами: числами, векторами, множествами, матрицами, функциями и т. д. В наиболее общем виде математическая модель объекта представляется уравнением
где X, Y – векторы управляемых и неуправляемых параметров модели.
В зависимости от способа исследования все математические модели принято делить на аналитическиеи алгоритмические. Аналитическое моделирование позволяет получить выходные результаты в виде конкретных аналитических выражений, использующих счетное число арифметических операций и переходов к пределу по натуральным числам. При этом частными случаями соответствующих моделей являются все корректные алгебраические выражения, а также та их часть, которая имеет умышленно ограниченное число параметров и применяется для получения приближенных результатов.
В отличие от аналитических алгоритмическиемодели могут учитывать практически любое число существенных факторов, а потому используются для моделирования наиболее сложных объектов и чаще всего с помощью мощных и быстродействующих компьютеров. Однако в большинстве подобных случаев алгоритмические модели позволяют получать лишь приближенные результаты, используя метод численного или имитационного моделирования.
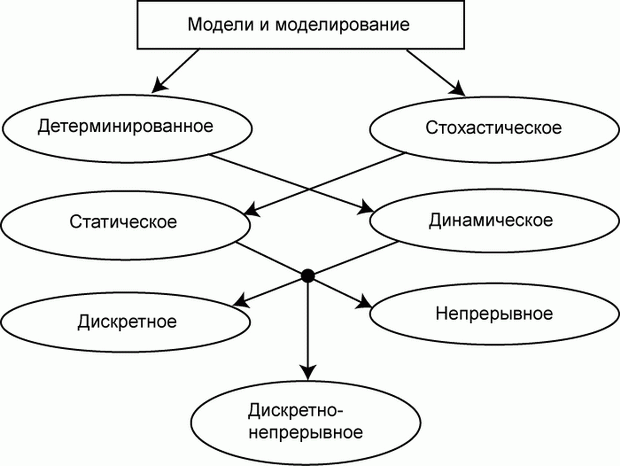
Еще одним признаком классификации математических моделей будет служить тип их входных и выходных параметров. Дело в том, что некоторые их группы нередко имеют различную «математическую природу», например, являясь постоянными величинами, или функциями, скалярами, или векторами, четкими или нечеткими подмножествами. Поэтому в зависимости от вида используемых параметров эти модели правомерно разделить на такие пять типов: детерминированные, стохастические, случайные, интервальные и нечеткие.
Перечисленные типы математических моделей отличаются между собой, прежде всего, по степени определенности или неопределенности своих параметров, обусловленной недостатком или спецификой имеющейся о них информации. Особое положение, соответствующее полной определенности, занимают детерминированныемодели. В них каждому параметру соответствует конкретное целое, вещественное или комплексное число либо соответствующая функция.
В стохастическоймодели значения всех или отдельных параметров определяются случайными величинами, заданными плотностями вероятности, чаще всего – нормально или экспоненциально распределенными. Несколько сложнее обстоит с определенностью случайноймодели, где некоторые или все параметры уже являются случайными величинами, найденными в результате статистической обработки ограниченной выборки и представленными в виде оценок соответствующих плотностей вероятности, а потому и менее точными.
Заметно более неопределенные параметры имеют интервальныемодели, в которых вместо точечных оценок их значений (как в предыдущем случае) используются интервальные. Нередко такие интервалы задаются лишь их граничными значениями (наименьшим и наибольшим из возможных). Примерно этот же способ представления параметров применяется и в нечеткихмоделях, которые уже оперируют нечеткими величинами или числами, также заданными на некоторых интервалах возможных значений [24].
Другими отличиями между интервальными и нечеткими моделями служат специфические правила арифметической и логической обработки нечетких параметров, а также нечеткие алгоритмы логического вывода относительно конечных результатов моделирования.
Рассмотренную классификацию не следует считать всеобъемлющей, так как ее можно продолжить, например, за счет классификации математических моделей, параметры которых имеют различное отношение, допустим: а) по времени – «статическая», «динамическая»; б) по размерности пространства – «одномерная», «многомерная». Имеют место и совершенно специфические модели и методы, характеризуемые неопределенностью своеобразного типа, например, той, которая рассматривается в теории игр. Ее принципиальное отличие проявляется, в том числе, и в необходимости учета злонамеренной целенаправленности соперников, обычно отсутствующей у объектов неживой природы.
4.3 Контрольные вопросы
1. На чем основан выбор методов моделирования?
2. На какие две группы можно разделить все методы моделирования?
3. В чем заключается математический метод моделирования?
4. В чем отличие детерминированных моделей от стохастических?
5. Приведите пример аналогового и физического методов моделирования.
6. В чем отличие семантического моделирования от вербального?
7. Объясните несимметричность иерархии классов методов моделирования.
8. Приведите примеры совместного применения двух или более методов моделирования для достижения цели.
9. Для чего нужен мысленный эксперимент?
10. Как формально можно представить математическую модель?
1. Информатика. Базовый курс. 2-е издание. Под ред. Симоновича С.В. – СПб.:Питер, 2005. – 640 с.
2. Могилев А.В., Пак Н.И., Хеннер Е.К. Информатика. – М.: Academia, 2004. – 848 с.
3. Информатика для юристов и экономистов. Под ред. Симоновича С.В. – СПб.:Питер, 2001. – 688 с.
4. Румянцева Е.Л., Слюсарь В.В. Информационные технологии. – М.: Форум, Инфра-М, 2007. – 256 с.
5. Информатика: Учебник / Под общ. ред. А.Н. Данчула. – М.: Изд-во РАГС, 2004. – 528 с.
6. Гук М.Ю. Аппаратные средства IBM PC. Энциклопедия. – СПб.: Питер, 2001. – 816 с.
7. Унру Н.Э. Основы организации ЭВМ и систем: Учеб. пособие. – Новосибирск: СГГА, 1999. – 113 с.
8. Шагурин И.И., Бердышев Е.М. Процессоры семейства Intel P6. Pentium, Pentium II, Pentium III и др. – СПб.: Питер, 2001. – 260 с.
9. Гук М., Юров В. Процессоры Pentium 4, Athlon, Duron. – СПб.: Питер, 2001. – 512 с.
10. Цилькер Б.Я., Орлов С.А. Организация ЭВМ и систем: Учебник для вузов. – СПб.: Питер, 2006. – 668 с.
11. Бройдо В.Л., Ильина О.П. Архитектура ЭВМ и систем: Учебник для вузов. – СПб.: Питер, 2006. – 718 с.
12. Колесниченко О., Шишигин И. Аппаратные средства PC. 4–е изд., перераб. и доп. – СПб.: БХВ – Петербург, 2001. – 847 с.
13. Нортон П., Гудман Дж. Внутрений мир персональных компьютеров. – 8–е изд. /Пер. с анг/. – Киев: Диа–Софт, 1999. – 584 с.
14. Перегудов Ф.И., Тарасенко Ф.П. Основы системного анализа: Учеб. 2-е изд., доп.-Томск: Изд-во НТЛ, 1997.-396 с.: ил.
16. Седов Л.И. Теория подобия и размерности в механике. –М.: ГИТТЛ, 1954.
17. Советов Б.Я., Яковлев С.А. Моделирование систем: Учеб. Для вузов – 3-е изд., перераб. И доп.- М.: Высш.шк., 2001. – 343 с.: ил.
18. Веников В.А., Веников Г.В. Теория подобия и моделирования. – М.: Высшая школа, 1984.
19. Вовк, И.Г. Введение в математическое моделирование: учеб. пособие / И.Г. Вовк. – Новосибирск: СГГА, 1997. – 45 с.
20. Угринович Н.Д. Информатика и информационные технологии. Учебник для 10-11 классов/ Н.Д.Угринович. – М.:БИНОМ. Лаборатория занятий, 2003. – 512 с.: ил.
22. Белов П.Г. Системный анализ и моделирование опасных процессов в техносфере: Учеб. Пособие для студ. высш. учеб. заведений/П.Г.Белов. – М.: Издательский центр «Академия», 2003. – 512 с.
24. Дюбуа Д., Прад А. Теория возможностей // Приложения к представлению знаний в информатике: Пер. с франц. – М.: Радио и связь, 1990. – 288 с.
Большая Энциклопедия Нефти и Газа
Материальное моделирование
Материальное моделирование подразделяется на физическое И предметно-математическое. Физическое моделирование предполагает использование для исследований моделей, имеющих одну и ту же физическую природу, с моделируемыми объектами. Оно основано на теории подобия и анализе размерностей. Физическая модель сохраняет геометрическое и физическое подобие параметров и процессов, происходящих в натурном объекте. Между значениями переменных величин, характеризующих явления в натурном объекте и модели, в определенные моменты времени должна соблюдаться пропорциональность. Величины, характеризующие процессы в физической модели и натурном объекте, определяются только масштабом. [1]
Итак, материальное моделирование может применяться для анализа экономических явлений в крайне ограниченном объеме. [4]
Другим частным случаем материального моделирования является аналоговое моделирование, основанное на аналогии явлений, имеющих различную физическую природу, но описываемых одинаковыми математическими уравнениями. [5]
Третья подгруппа методов материального моделирования связана с использованием материальных моделей, имеющих другую физическую природу, по описывающихся теми же математическими соотношениями, что и изучаемый объект. Такое моделирование называется аналоговым и основывается па аналогии в математическом описании модели и объекта. [6]
Однако и в материальном моделировании важную роль играют мысленные модели. Не имея мысленной модели оригинала, невозможно ни решить, какой должна быть материальная модель, ни распространить результаты моделирования на оригинал. Поэтому и при таком суженном понимании моделирования его теория в значительной мере связана с изучением мысленных моделей. [7]
Подчеркнем, что в обоих типах материального моделирования модели являлись материальным отражением исходного объекта и были связаны с ним своими геометрическими, физическими или другими характеристиками. [8]
Подобие, а соответственно и модели, разделяют на мыслен-н ы е, отвечающие любым видам мысленных экспериментов, и м а-т е р и а л ь н ы е, предусматривающие ту или иную конструктивную реализацию модели. Материальное моделирование оперирует с моделями разнообразного исполнения и разбивается на три большие группы. [10]
В настоящее время выделяются два основных метода моделирования: материальное и мысленное. Материальное моделирование включает следующие виды. [11]
Таким образом, материальное моделирование по своей природе является экспериментальным методом. [12]
Материальным моделирование называется в том случае, когда исследование ведется на моделях, связь которых с исследуемыми объектами существует объективно, имеет материальный характер. Модели в этом случае либо строятся исследователем, либо отбираются им в окружающем его мире. В материальном моделировании можно условно выделить три основные подгруппы методов: пространственное, физическое и аналоговое моделирование. [14]
Понятие модели и моделирования
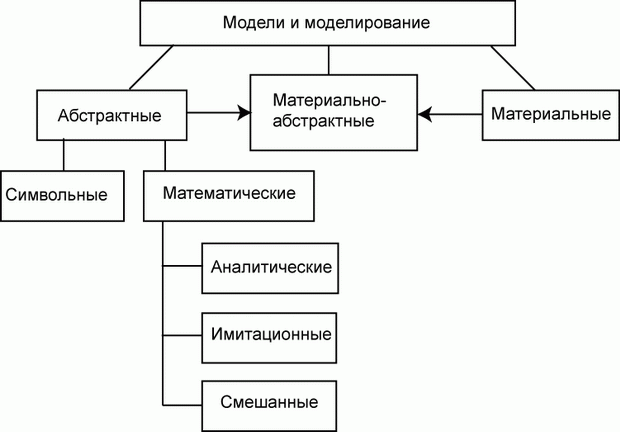
1.2.3. Классификация моделей и моделирования по признаку «способ реализации модели»
Согласно этому признаку модели делятся на два обширных класса:
Нередко в практике моделирования присутствуют смешанные, абстрактно-материальные модели.
Абстрактные модели представляют собой определенные конструкции из общепринятых знаков на бумаге или другом материальном носителе или в виде компьютерной программы.
Абстрактные модели, не вдаваясь в излишнюю детализацию, можно разделить на:
Символическая модель может иметь самостоятельное значение, но, как правило, ее построение является начальным этапом любого другого моделирования.
Математические модели могут быть:
Преобразование математических моделей по известным законам и правилам можно рассматривать как эксперименты. Решение на основе аналитических моделей может быть получено в результате однократного просчета безотносительно к конкретным значениям характеристик («в общем виде»). Это наглядно и удобно для выявления закономерностей. Однако для сложных систем построить аналитическую модель, достаточно полно отражающую реальный процесс, удается не всегда. Тем не менее, есть процессы, например, марковские, актуальность моделирования которых аналитическими моделями доказана практикой.
В чем заключается отличие имитационных и аналитических моделей?
В случае аналитического моделирования ЭВМ является мощным калькулятором, арифмометром. Аналитическая модель решается на ЭВМ.
Имитационные модели достаточно просто учитывают влияние случайных факторов. Для аналитических моделей это серьезная проблема. При наличии случайных факторов необходимые характеристики моделируемых процессов получаются многократными прогонами (реализациями) имитационной модели и дальнейшей статистической обработкой накопленной информации. Поэтому часто имитационное моделирование процессов со случайными факторами называют статистическим моделированием.
Если исследование объекта затруднено использованием только аналитического или имитационного моделирования, то применяют смешанное (комбинированное), аналитико-имитационное моделирование. При построении таких моделей процессы функционирования объекта декомпозируются на составляющие подпроцессы, и для которых, возможно, используют аналитические модели, а для остальных подпроцессов строят имитационные модели.
1.3. Этапы моделирования
Первый этап: уяснение целей моделирования. Вообще-то это главный этап любой деятельности. Цель существенным образом определяет содержание остальных этапов моделирования. Заметим, что различие между простой системой и сложной порождается не столько их сущностью, но и целями, которые ставит исследователь.
Обычно целями моделирования являются:
Третий этап: выбор языка программирования или моделирования, разработка алгоритма и программы модели. Модель может быть аналитической или имитационной, или их сочетанием. В случае аналитической модели исследователь должен владеть методами решения.
В истории математики (а это, впрочем, и есть история математического моделирования) есть много примеров тому, когда необходимость моделирования разного рода процессов приводила к новым открытиям. Например, необходимость моделирования движения привела к открытию и разработке дифференциального исчисления (Лейбниц и Ньютон) и соответствующих методов решения. Проблемы аналитического моделирования остойчивости кораблей привели академика Крылова А. Н. к созданию теории приближенных вычислений и аналоговой вычислительной машины.
Четвертый этап: планирование эксперимента. Математическая модель является объектом эксперимента. Эксперимент должен быть в максимально возможной степени информативным, удовлетворять ограничениям, обеспечивать получение данных с необходимой точностью и достоверностью. Существует теория планирования эксперимента, нужные нам элементы этой теории мы изучим в соответствующем месте дисциплины.
Пятый этап: выполнение эксперимента с моделью. Если модель аналитическая, то эксперимент сводится к выполнению расчетов при варьируемых исходных данных. При имитационном моделировании модель реализуется на ЭВМ с фиксацией и последующей обработкой получаемых данных. Эксперименты проводятся в соответствии с планом, который может быть включен в алгоритм модели. В современных системах моделирования такая возможность есть.
На этом рассмотрение последовательности моделирования закончим, сделав весьма важный вывод о необходимости документирования результатов каждого этапа. Это необходимо в силу следующих причин.
Во-первых, моделирование процесс итеративный, то есть с каждого этапа может осуществляться возврат на любой из предыдущих этапов для уточнения информации, необходимой на этом этапе, а документация может сохранить результаты, полученные на предыдущей итерации.
Во-вторых, в случае исследования сложной системы в нем участвуют большие коллективы разработчиков, причем различные этапы выполняются различными коллективами. Поэтому результаты, полученные на каждом этапе, должны быть переносимы на последующие этапы, то есть иметь унифицированную форму представления и понятное другим заинтересованным специалистам содержание.