что такое математический объект

Что такое математический объект

Беседа 4. Математические объекты

Математика, как и другие науки, изучает окружающий нас мир, природные и общественные явления, но изучает лишь особые стороны этих явлений.

В других случаях, кроме формы и размера, учитывают еще взаимное расположение частей фигуры.

Такие математические объекты, как числа, образуются путем выделения при рассмотрении различных совокупностей (множеств) однородных предметов таких общих свойств, как количество предметов в совокупности или их порядок следования, абстрагируясь от всех других свойств этих предметов (их неодинаковости, материала, цвета, величины и т. д.).

Итак, математика изучает особые идеальные математические объекты, которые образуются путем сложной мыслительной деятельности людей в процессе познания количественных свойств и отношений, а также пространственных свойств и форм предметов и явлений окружающего мира.

Поэтому первое, чему надо учиться в математике,- это умению в процессе изучения каких-то предметов или явлений для решения задач по определению количественной стороны или пространственных соотношений этих предметов или явлений образовывать, создавать математические объекты. Рассмотрим в качестве примера такую задачу.

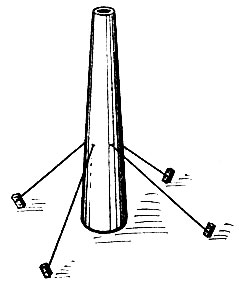
Задача.Для того чтобы укрепить железную дымовую трубу, было решено на высоте 20 м от ее основания прикрепить растяжки из стального каната, которые закрепить к четырем бетонным тумбам, находящимся на расстоянии 15 м от основания трубы. Сколько каната для этого потребуется? (Рис. 2.)

Рис. 2

Вообще надо помнить, что математическое решение любой практической задачи всегда является приближенным.

Для того чтобы закрепить полученные знания и проверить себя, как вы их усвоили, выполните следующее задание.

2.1. Какие геометрические фигуры выступают в качестве идеальных образов (моделей) реальных предметов в следующих практических задачах:

а)Найти площадь пятикопеечной монеты.

б) Найти длину обруча.

в) Найти площадь комнаты.

От каких свойств реальных предметов мы при этом абстрагируемся, а какие учитываем?

2.2. За билетами в театр стоит очередь. Какие математические объекты характеризуют положение (место) каждого человека в этой очереди? Какие практические задачи можно решить с помощью этих математических объектов?

2.3. Велосипедист выехал из города А в 9 ч утра и прибыл в город В, отстоящий от А на расстоянии 60 км, в 12 ч дня. Отдохнув в В 2 ч, он поехал дальше в город С, отстоящий от В на 72 км, и прибыл туда в 6 ч вечера.

Как можно наиболее просто и наглядно математически описать событие поездки велосипедиста из А в С? Какие практические задачи можно решить, имея это математическое описание? Какие математические объекты при этом использованы?

Источник

Единая природа математических объектов

В природе существует четыре основные первичные элементы структур, как составляющие десятирицы: монады, диады, триады и тетрады. В математике одни считают, что имеются скаляры, векторы и билинейные формы и тензоры, частными случаями последних являются все предыдущие. Другие представляют, что тензор обобщает понятия скаляра, вектора и матрицы и что привычные математические объекты лишь частные примеры более общего понятия, коим является тензор.
Кто прав? Чтобы разобраться в этом, необходимо выяснить физическую сущность математических объектов.

Математика вместе с языком, искусством и изобретательством образовывают систему мыслительной деятельности человека. Вместе с тем она сама является системой, так как содержит все присущие системам атрибуты.

Она существует в среде, которая является источником своего существования. Это можно представить, как множества с математическими объектами. В математике осуществляются какие-то операции, как аналог функционирования системы.
Она имеет свои фазовые состояния. У нее есть неопределенности, взаимодействия и преобразования. С ее помощью формулируются задачи, которые имеют решения, что аналогично органу саморегуляции в естественных системах или органу управления в искусственных системах.

Математика должна быть построена по образу и подобию естественных систем, тогда она будет способна предсказать то, что существует, но пока недоступно человеческому сознанию. Так оно, в принципе и есть, но не всегда и не везде.
Даже если математика построена на ложных физических принципах, то ее формулы работают, а теория создает некие фантастические конструкции. Так случилось и с теорией относительности, и с квантовой механикой.

Это свидетельствует о том, что законы в математике и в реальной действительности одни и те же, только сформулированы по-другому. Однако математика может «оторваться» от реальной действительности и изобрести такие конструкции, которые не существуют в реальности. В связи с этим возникает вопрос: а нужна ли человеку такая математика, которая ничего не отображает в настоящем и не может ничего отобразить в будущем?

Для того, чтобы такого не случалось, надо математику строить по законам естественного развития Природы. Прежде всего, необходимо рассмотреть единичные объекты Природы и их аналоги в математике, т.е. естественные количественные объекты и их меру.

Особенностью этих элементов является то, что каждый последующий содержит все предыдущие. Комплекс содержит два скаляра, вектор – три комплекса, в которых по два скаляра, тензор – четыре вектора, в которых по три комплекса, содержащих по два скаляра. Получается цепочка скаляров: 1-2-6-10 (рисунок). Это напоминает расположение электронов и орбит атома. Видимо не случайно.

Вообще говоря, в математике считается, что «те;нзор (от лат. tensus, «напряженный») — объект линейной алгебры, линейно преобразующий элементы одного линейного пространства в элементы другого». Или «тензор – это математический объект, который как объект не зависит от смены системы координат, но его компоненты при смене системы координат преобразуются по определенному математическому закону»

Здесь, очевидно, следует уточнить природу математических объектов. С одной стороны, меньшие образовывают большие, а большие распадаются на меньшие. Видимо, это не одно и то же. Два скаляра образуют комплекс, три комплекса – вектор, четыре вектора – тензор. А распадаются они в обратной последовательности. Поэтому, говорить о том, что меньшие являются частным случаем больших, вряд ли обоснованно.

Все структурные элементы могут существовать не только как самостоятельные целостные объекты, являясь элементами множеств, но и как среды (источники) существования систем.

Например, у естественных и технических систем таким источником является энергия, у производственных систем источником существования служат сырьевые ресурсы. Есть сырье – производство работает, нет сырья – производство стоит. Таких примеров много, где в качестве источника существования выступают, либо монады (скаляры), либо диады (комплексы), либо триады, (векторы) либо тетрады (тензоры).

Источник

Робкие шаги

Тот неловкий момент, когда призываешь подучить математику и не знаешь, с чего начать. Да и начинать надо максимально демократично, т.е. предполагая, что читатель ничего из этого не слышал, а если случайно и услышал, то старался поскорее забыть. Но и заново складывать палочки — затея не из лучших. В конце концов, именно складывание палочек во многом и привело к нынешней печальной ситуации. Мы же собираемся не навык нарабатывать, а расширять сознание.

Пересчёт же палочек, кстати, плох именно этим. Человек слишком привыкает думать о числах как о палочках, в результате чего более изящные действия, нежели наглядные арифметические, как и нестандартные понятия, вызывают неподдельный испуг, потливость ладоней и учащённое сердцебиение. В общем, палочки это плохо, понятненько?

Математические объекты

Чем тогда займёмся? Небольшим обобщением. Перед нами стоит задача изучения математики, а значит, сами объекты изучения есть объекты математические. Что такое математический объект? Никто не знает. В смысле, вы нигде не найдёте описания более подробного, чем то, что это «объект, изучаемый в математике». Положение дел во многом напоминает ситуацию, описанную в известном анекдоте: человек приходит вечером домой и обнаруживает, что его сосед по квартире разрубил на доски шкаф и жарит на нём мясо, а на вопрос «что это всё такое?» отвечает «это шашлык».

На деле оказывается, что математический объект — это любой объект с формализованными свойствами, которые при этом не противоречат друг другу. При желании вы можете самостоятельно придумать множество таких объектов, а потом приняться их изучать. Благодаря тому, что свойства одних объектов кучей образов пересекаются со свойствами других, возникают различные структуры, отношения, зависимости. Тут начинается извечное соревнование между чисто описательным подходом и интуитивным, при этом мы будем стараться делать выбор в пользу второго.

Математический объект. Под математическим объектом подразумевается любой воображаемый объект, о котором можно делать формальные утверждения.

Скажем, объяснить, что такое сэндвич, можно разными способами. Чисто формально правильным будет сказать, что это кусок серого хлеба, лист салата, кусочки огурчика и нарезанная копчёная грудинка. Кто же от такого сэндвича откажется? Но что случится, если вам встретится комбинация из чёрного хлеба, помидоров и бекона, распознаете ли вы это всё как сэндвич или нет? Скорее всего нет, если у вас отсутствует интуитивное, общее понимание сэндвича как сочетания какой-то углеводной хлебной базы с относительно питательной начинкой (про омерзительное порождение больного разума вроде «вегетарианского сэндвича» говорить не будем).

В отличие от реальных и остро стоящих перед нами кулинарных вопросов, с точки зрения математики совершенно безразлично, является ли отдельно взятый описываемый объект моделью чего-то «реально существующего» или нет. Даже в тех областях математики, чьи достижения едва ли можно будет когда-то применить практически, кипят споры и делаются настоящие открытия. Да и сами объекты, берущие за образец «реально существующее», всё же слишком условны. Например, квадратный кусок булки для бургера в строгом смысле квадратным не является.

Математические операции

Помимо многократно упомянутых объектов как таковых, нас также интересуют операции, которые с ними можно осуществлять. Операции — это такие действия, которые принимают математические объекты в качестве входящих данных и что-то с ними делают по описанным правилам, возвращая результат.

Операция. Математической операцией называется любое действие, которое берёт несколько математических объектов и что-то с ними делает, выдавая по итогам результат операции.

Хочется верить, что вы успели заметить непозволительное количество мутных, неясных словечек, с трудом представляемых на языке формул и цифр. Увы, это всё издержки естественного языка и человеческого мышления в принципе. Теории, где у всех элементов есть однозначные определения, просто-напросто невозможны (об этом мы ещё поговорим), и это с 1930-х выступает причиной немалой грусти огромной армии ортодоксальных формалистов.

Несмотря на всю любовь к точности, «точная наука математика» не является абсолютно точной и последовательной. Все надежды на то, что она такой станет, в 20-м веке подошли к концу. Поэтому как бы рьяно кто-то из знакомых технарей вам ни рассказывал, что он не гуманитарий какой-то, в своих размышлениях никаких допущений не делает, всё у него по полочкам, знайте, что он не договаривает. По возможности, конечно, используйте эти наблюдения чтобы максимально пристыдить и унизить окружающих!

Концептуально математическая операция ничем не отличается от любой из своих коллег в реальном мире. К примеру, можно рассмотреть операцию на типичной вечеринке: вы хотите успеть домой, но не хотите платить за такси, предпочитая метро. Очевидным решением будет подойти к кому-то из местных и спросить, во сколько нужно выйти, чтобы не опоздать. Следопыты наверняка обратят внимание на текущее время и степень вашего опьянения, после чего назовут примерный интервал. Иными словами, они возьмут несколько не подлинно математических объектов, проведут нам ними операцию и получат третий, не имевшийся до этого, который и станет их итоговым вердиктом.

Формальная запись

Ко всему этому математика добавляет лишь требование формальной записи происходящего, а в остальном стесняет вас даже меньше, чем правила общественного приличия на подобных мероприятиях.

То есть, мы должны говорить о чём-то конкретном, например, о неких и , или же и , если хочется экзотики.

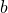
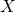
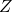
Сами буквы, которыми обозначаются объекты, не играют никакой роли (если об этом не было заявлено изначально) и представляют собой дань исторически сложившимся традициям, именно поэтому с ними иногда столько проблем.

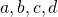
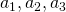
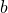
На практике следующие рядом буквы алфавита и т.п. могут использоваться, когда объектов не так много и их важно друг от друга отличать. Одни и те же буквы, но с разными индексами, полезнее, когда мы ведём речь о значительных количествах. В таком случае появляются и многие другие. В зависимости от буквы, объекты могут различаться по своей природе, если все это номера в вашей записной книжке, то это уже количество людей во френд-листе.

При перечислении мы прибегли к трюку — в обозначение каждого нового объекта подставили цифру, позволяющую отличить его от другого. Мы использовали нижний индекс, но можно писать и в верхнем, например, и так далее. Такая запись возможна, но означает не порядок элементов, а слегка другую операцию, про которую вам пока знать не положено, даже не спрашивайте. Почему цифра снизу это личный номер, а сверху — показатель степени? А просто потому, что так сложилось, и все этим пользуются.

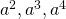
Если видишь, что буквы пошли, всякие там 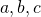и подобное, значит, разговор на общие темы сейчас. Сам подумай, я тебе могу на примерах говорить, что и как по жизни работает, а могу типа глобально сказать, если ты паренёк смышлёный и голова как надо работает. С нормальными людьми я так и говорю, «работу делай по совести», а не про каждое задание объясняю. Занятой я, некогда одно и то же растолковывать.

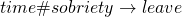
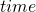
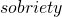
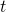
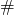
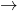
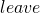
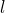
С записью операций дела обстоят не сильно сложнее. Чуть выше мы уже говорили об операции по оценке времени выхода из помещения. Всё это можно записать как . Имена и вводным данным присвоили для собственного удобства, их вполне можно заменить на и соответственно. Значок решётки в нашем случае это сама операция по оценке, а стрелочка призвана обратить наше внимание на то, что из этих данных получается некий результат , который мы также можем называть .

Свойства операций

Что мы можем сказать про нашу операцию? Если люди, к которым мы обращаемся за данной консультацией, не страдают отклонениями мышления, то они должны давать нам ответы независимо от порядка предоставления данных. Иными словами, фраза «я слегка накурен, сейчас половина одиннадцатого» должна приводить ровно к такому же результату, как и «сейчас половина одиннадцатого, я слегка накурен». Говоря формально, 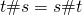. Значок говорит о том, что объекты по обе стороны от него идентичны (речь идёт об одном и том же объекте, записанном разными способами). Небольшой житейский совет — если вы накурены, то закладывайте на любое путешествие время, в полтора раза больше привычного.

Если наше предположение верно, то как мы ни спрашивай, ответ всегда будет одинаковым. В этом случае говорят, что мы имеем дело с коммутативной операцией. В самом слове «коммутативной» нет ничего ласкающего слух, это обычный термин, который используется, чтобы не тратить много времени на формулировки. Согласитесь, сказать «операция коммутативна» намного проще, чем «операция возвращает одно и то же значение независимо от порядка операндов». «Операнд«, если что, это математический объект, который берётся для операции. 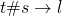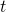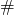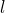В нашем случае получается, что и это операнды (или, как ещё говорят, аргументы), это операция (или знак операции), ну а это результат операции (или значение).

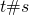
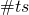
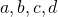
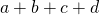
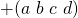
Дадим волю внутреннему бунтарю и спросим, с какой стати мы вообще пишем , почему, к примеру, не , иначе говоря, почему знак операции размещается между объектами, а не, допустим, слева от них? Никакого чёткого ответа не получим и здесь. Ничего не мешает нам писать знак операции с какой-то отдельной стороны, например, сумму элементов (о которой вы также пока ничего не знаете) вполне можно записать как , а можно и как . Последний метод известен как польская запись (польская нотация) и в математике используется редко, зато крайне популярен у [бородатых] программистов. Очевидно, в случае с большим количеством аргументов он предпочтительнее. Но дело не в польской или какой ещё записи, ведь нужно всегда задаваться вопросом, что откуда взялось и почему так работает.

Запись операции. Как правило, математические выражения, включающие операции, состоят из операндов (объектов, с которыми проводится операция, например, объекты под названием и т.п.), оператора (знак, обозначающий операцию, например, и так далее). Результат операции или указывается, или его требуется найти самостоятельно.

Звучит пока просто, но так ли это легко на самом деле? Да, это и в самом деле не требует гениальности. Все эти выражения не несут никакого скрытого смысла, это просто термины, которые не ясны окружающим ровно в той же степени, в которой шизофазическим бредом выглядит речь любителей Dota 2 или Pokemon Go.

Чтобы окончательно победить страх над непонятыми выражениями, закончим разбором одного из них.

При рассмотрении всё тех же операций упоминают о некой арности. Что такое арность операции? Это всего-навсего количество операндов/аргументов, которое эта операция принимает. Если операнд может быть только один, то операция унарная. Если два, то бинарная. Если три — дело совершенно точно идёт о триарной операции. А если их может быть сколько угодно, то перед нами операция мультиарная.

К примеру, наша операция 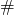оказалась бинарной, как и знакомое почти каждому человеку обычное сложение. В дальнейшем почти все (или вообще все) операции, которые мы будем изучать, будут бинарными, но за нашим уютным арифметическим болотом всегда бурлит бездонный океан.

Зачем нам вообще было это знать? Теперь мы можем заявить окружающим, что потратили вечер на создание коммутативной бинарной операции. Просто произнесите это, «коммутативная бинарная операция». Что, уже начинаете ощущать принадлежность какому-то высшему сословию?

Источник

Что такое математический объект

1. нБФЕНБФЙЮЕУЛЙК ПВЯЕЛФ ЛБЛ БВУФТБЛГЙС ПФ БВУФТБЛГЙЙ

чУЕ ЬФП, ВЕЪХУМПЧОП, УРТБЧЕДМЙЧП: Й ЧЩУПЛБС БВУФТБЛФОПУФШ, Й «ЦЕУФЛПУФШ», Й ПРПУТЕДПЧБООПУФШ. оП ЬФП ЕЭЕ ОЕ ЧУС РТБЧДБ П НБФЕНБФЙЛЕ.

дПУФБФПЮОП ПФЧМЕЮЕООПК УФЕРЕОЙ ПВЭОПУФЙ Й ДБЦЕ ЧУЕПВЭОПУФЙ ЧМБДЕАФ Й ОЕЛПФПТЩЕ ДТХЗЙЕ ОБХЛЙ. оЕ ФПМШЛП ЖЙМПУПЖЙС, Б ФБЛЦЕ ЖЙЪЙЛБ, МПЗЙЛБ. тБЧОП Й ИБТБЛФЕТЙУФЙЛБ «ЦЕУФЛПУФЙ». чППВЭЕ, ДЕМБС ЪБСЧМЕОЙС ПФОПУЙФЕМШОП ЖЙЪЙЮЕУЛЙИ ПВЯЕЛФПЧ, ОЕ РТЙИПДЙФУС ЗПЧПТЙФШ П РПУФПСОУФЧЕ УФТХЛФХТ Й ТБЪНЕТОПУФЕК, РПУЛПМШЛХ ОБ ЗТБОЙГБИ ФЕМ ОЕРТЕТЩЧОП УПЧЕТЫБАФУС РЕТЕНЕОЩ, РПДФБЮЙЧБАЭЙЕ ЙОЧБТЙБОФОХА УФТПЗПУФШ. фЕН ОЕ НЕОЕЕ Ч ПРТЕДЕМЕООЩИ ТБНЛБИ ЬФЙ ПВЯЕЛФЩ РТЙОЙНБАФУС УЕВЕФПЦДЕУФЧЕООЩНЙ. уЮЙФБЕФУС, ЮФП НБФЕНБФЙЮЕУЛЙЕ ПВЯЕЛФЩ Ч ОБЙВПМШЫЕК УФЕРЕОЙ ХДПЧМЕФЧПТСАФ ЪБЛПОХ ФПЦДЕУФЧБ, ЙВП ПОЙ ОБУФПМШЛП ПВТБВПФБОЩ НЩУМША, ЮФП ЙН ОЕ ПУФБЧМЕОП ЧПЪНПЦОПУФЙ ДМС ЛБЛЙИ ВЩ ФП ОЙ ВЩМП ЙЪНЕОЕОЙК. оП ЧПФ, ЮФП ПФНЕЮБЕФ м.чЙФЗЕОЫФЕКО.

чПЪШНЕН УФТПЛХ, УПУФБЧМЕООХА ЙЪ УФБ НЙММЙПОПЧ НБФЕНБФЙЮЕУЛЙИ ЪОБЛПЧ. б ЪБФЕН ЧЕТОЕНУС Л ОЕК, УЛБЦЕН, ЮЕТЕЪ ПДЙО ЮБУ. тБЪЧЕ ПОБ ЪБ ЬФП ЧТЕНС ОЕ НПЦЕФ ЙЪНЕОЙФШУС? чЕДШ УФТПЛБ У РПДПВОЩН ЛПМЙЮЕУФЧПН ЪОБЛПЧ ОЕПВПЪТЙНБ ЪБ ХЛБЪБООЩК УТПЛ ЧТЕНЕОЙ. йОБЮЕ УЛБЪБФШ, УЧЕТИДМЙООЩЕ УФТПЛЙ ЪОБЛПЧ ПЛБЪЩЧБАФУС ОЕЦЕУФЛЙНЙ Й РПФПНХ Л ОЙН ОЕ ДПМЦОП ВЩФШ ДПЧЕТЙС. уМЕДПЧБФЕМШОП, Й РП РБТБНЕФТХ «ЦЕУФЛПУФЙ» НБФЕНБФЙЮЕУЛЙЕ ПВЯЕЛФЩ ПФМЙЮБАФУС ПФ ПВЯЕЛФПЧ, У ЛПФПТЩНЙ ПРЕТЙТХАФ ДТХЗЙЕ ОБХЛЙ, Ч МХЮЫЕН УМХЮБЕ МЙЫШ ЛПМЙЮЕУФЧЕООПК НЕТПК.

оБЛПОЕГ, УЧПКУФЧП НБФЕНБФЙЛЙ РТЕДУФБЧМСФШ ПРПУТЕДПЧБООПЕ ПФОПЫЕОЙЕ Л НЙТХ. ч ЬФПН ПУПВПК РТЙЧЙМЕЗЙЙ Х ОЕЕ ОЕФ. мАВБС ОБХЛБ, ЕУМЙ ПОБ ЦЕМБЕФ ВЩФШ ФЕПТЕФЙЮЕУЛПК, БДТЕУХЕФ УЧПЙ ЧЩУЛБЪЩЧБОЙС ТЕБМШОПУФЙ ОЕ РТСНП, Б ЮЕТЕЪ ЛПОГЕРФХБМШОЩЕ УЙУФЕНЩ, ДПВЩФЩЕ МПЗЙЛП-ЗОПУЕПМПЗЙЮЕУЛПК ТЕЛПОУФТХЛГЙЕК ЮХЧУФЧЕООП ДБООПЗП. фБЛ, Ч ЛМБУУЙЮЕУЛПК НЕИБОЙЛЕ НБФЕТЙБМШОЩЕ ФЕМБ РТЕДУФБЧМЕОЩ ЙДЕБМЙЪЙТПЧБООЩНЙ ПВТБЪБНЙ НБФЕТЙБМШОЩИ ФПЮЕЛ Й БВУПМАФОП ФЧЕТДЩИ ФЕМ. ч ЕЭЕ ВПМШЫЕК УФЕРЕОЙ ФЕПТЕФЙЮОЩ Й ПРПУТЕДПЧБОЩ РПОСФЙС ОЕЛМБУУЙЮЕУЛПК ЖЙЪЙЛЙ.

фЕРЕТШ ЧПЪШНЕН НБФЕНБФЙЮЕУЛПЕ РПОСФЙЕ. оБРТЙНЕТ, ЮЙУМП, РТЙФПН, ЧОБЮБМЕ ОЕ БВУФТБЛФОПЕ ЮЙУМП ЧППВЭЕ, Б ЛПОЛТЕФОПЕ: 5, 7, 8 12 Й Ф.Д.

лПОЕЮОП, БВУФТБЛГЙЙ, (ЛБЛ Й БВУФТБЛГЙЙ ВПМЕЕ ЧЩУПЛЙИ РПТСДЛПЧ) ЙНЕАФ НЕУФП Й Ч ДТХЗЙИ ОБХЛБИ. лТПНЕ ФПЗП, РПУМЕДОЙЕ ПРЕТЙТХАФ Й НБФЕНБФЙЮЕУЛЙНЙ ПВЯЕЛФБНЙ (ПУПВЕООП ЖЙЪЙЛБ). оЕ ЪОБЮЙФ МЙ ЬФП, ЮФП Х НБФЕНБФЙЛЙ ОЙЛБЛПК УРЕГЙЖЙЛЙ ОЕФ?

дЕМП Ч ФПН, ЮФП УПВУФЧЕООП НБФЕНБФЙЮЕУЛЙК РПДИПД ПФМЙЮБЕФУС ПФ ПУФБМШОЩИ ОБХЛ. фБЛ Ч УМХЮБЕ У ЮЙУМБНЙ. пРЕТЙТХС У УПЧПЛХРОПУФСНЙ ЛПОЛТЕФОЩИ ПВЯЕЛФПЧ Й УФБЧС ЙИ Ч ПДОП-ПДОПЪОБЮОПЕ УППФЧЕФУФЧЙЕ (ФП ЕУФШ ПВТБЪХС НБФЕНБФЙЮЕУЛХА БВУФТБЛГЙА ЮЙУМБ), НБФЕНБФЙЛ ОЕ БОБМЙЪЙТХЕФ УЧПКУФЧБ ЧИПДСЭЙИ Ч УПЧПЛХРОПУФЙ ПВЯЕЛФПЧ. пО ВЕТЕФ Ч ЛБЮЕУФЧЕ ЙУИПДОПК БВУФТБЛГЙЙ УБНЙ УПЧПЛХРОПУФЙ, ЪДЕУШ ЧБЦОП ОЕ «ЮФП», Б «УЛПМШЛП». фП ЕУФШ Ч БМЖБЧЙФ НБФЕНБФЙЮЕУЛПЗП СЪЩЛБ ЧЛМАЮБАФУС ПВЯЕЛФЩ ОЕ ОЙЦЕ РЕТЧПЗП ФЙРБ (ЛМБУУЩ, ЛМБУУЩ ЛМБУУПЧ Й Ф.Д.). ч ДТХЗЙИ ЦЕ ОБХЛБИ БМЖБЧЙФ УПУФБЧМЕО ЙЪ ПВЯЕЛФПЧ ОХМЕЧПЗП ФЙРБ (ЧЕЭЙ). рПДТПВОЕЕ ПВ ЬФПН Ч УЧСЪЙ У ФЕПТЙЕК ФЙРПЧ в. тБУУЕМБ (ЗМ. V, 4). бОБМПЗЙЮОП ФПЮЛБ Ч ЖЙЪЙЛЕ ИПФС Й ОЕ ЙНЕЕФ ЙЪНЕТЕОЙК, ОП ПВМБДБЕФ НБУУПК, НБФЕНБФЙЮЕУЛБС ЦЕ ФПЮЛБ ОЕ ОБДЕМЕОБ ОЙЛБЛЙНЙ ЖЙЪЙЮЕУЛЙНЙ УЧПКУФЧБНЙ. уЧПКУФЧП ЦЕ ТБЪНЕТОПУФЙ РХФЕН РТЕДЕМШОПЗП РЕТЕИПДБ УЧЕДЕОП Л ОХМА.

Источник