что такое мантисса целого числа
Что такое мантисса и порядок числа
Содержание статьи
Значение мантиссы
Мантисса – одна из частей числа, которое представлено форматом с плавающей точкой. Второй частью этого числа является показатель степени. По сути, это дробная составляющая логарифма.
Значение мантиссы в том, что по ней находится число, которое является источником логарифма. Целая часть показывает только степень десяти или тривиальный множитель, тогда как сама мантисса показывает, какое именно число должно быть умножено на тривиальный множитель, который имеет вид 0,001 или 100.
Экспоненциальная запись представляет это в следующем виде: N = M*n^p, где мантиссой является M. Для примера можно взять число 3600 и представить его в экспоненциальной записи. Получится следующее: 3600 = 3,6*10^3. Учитывая вышесказанное, мантиссой будет являться число 3,6.
Важно понимать, что число, имеющее плавающую запятую, также имеет изменяющуюся абсолютную точность и фиксированную относительную точность. Использование чисел с плавающей запятой лучше, чем представление чисел с фиксированной запятой, так как есть возможность применения большого диапазона значений, тогда как относительная точность не меняется. Это поможет понять следующий пример: форма, имеющая фиксированную запятую, позволяет представить число, которое занимает 2 разряда после запятой и 8 разрядов в целой части, в виде 8765,43; 123456,78 и так далее. Если же брать формат, имеющий плавающую запятую, можно произвести следующую запись: 1,2345678; 0,000012345678 и так далее. Однако для того, чтобы так сделать, важно иметь двухразрядное дополнительное поле, позволяющее записать показатели степени 10, начиная от 0 и кончая 1610. Общее число разрядов составит 10, то есть 8+2.
Мантисса, как для отрицательных, так и для положительных чисел, выражается в прямом коде. Различие в знаке будет отражено лишь в значении знакового разряда. Однако мантисса числа не может превышать единицы. Обычно точка в мантиссе располагается с левой стороны от старшего разряда. Для того, чтоб получить истинное значение числа, нужно умножить мантиссу на 16 в степени порядка. Порядок, полученный этим путем, называется характеристикой. Получается, что характеристика, которая отсчитывается от 64, будет всегда положительной.
В нормальной записи мантисса числа — всегда правильная дробь. Ее запись в ячейку производится так же, как запись числа с запятой в ячейку машины. Запятая фиксируется перед первым разрядом цифрового вида.
Мантисса числа, имеющая плавающую запятую, выражается шестнадцатеричными цифрами, при этом запятая располагается слева от самой высокой цифры мантиссы
Форма мантиссы
Есть две формы, позволяющие понять место применения мантиссы. Первая — нормальная форма числа. Эта форма, которая имеет мантиссу без учета знака на полуинтервале, то есть [0; 1) (0le a
Число с плавающей запятой состоит из:
* Мантиссы (выражающей значение числа без учёта порядка)
* Знака мантиссы (указывающего на отрицательность или положительность числа)
* Порядка (выражающего степень основания числа, на которое умножается мантисса)
* Знака порядка
[править] Нормальная форма и нормализованная форма
Что ты хочешь узнать?
Ответ
Нормализация мантиссы позволяет сэкономить один разряд в ее двоичном представлении. В обоих случаях заранее известно, что первый значащий разряд равен единице, поэтому его можно не хранить. Иногда это называется использованием неявного старшего бита.
Нормализация мантиссы результата независимо от режима не выполняется.
Нормализация мантиссы результата заключается в повторении операции сдвига мантиссы на один десятичный разряд с обнулением младшего разряда, а также в уменьшении порядка на единицу до тех пор, пока в знаковом разряде К2 ( Д9) не будет находиться наибольшая значащая цифра мантиссы. При переполнении разрядной сетки в области мантиссы выполнение этой процедуры может привести к переполнению разрядной сетки в области порядка.
00111001000100100000000000000000 – нули слева убираем:
111001000100100000000000000000 – нормализуем мантиссу:
1.11001000100100000000000000000 х 2^29.
Стандартная форма записи числа, мантисса числа, порядок числа
Положительное число, записанное в стандартной форме, имеет вид
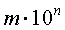
Число m является натуральным числом или десятичной дробью, удовлетворяет неравенству
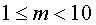
и называется мантиссой числа, записанного в стандартной форме.
Число n является целым числом (положительным, отрицательным или нулем) и называется порядком числа, записанного в стандартной форме.
Например, число 3251 в стандартной форме записывается так:
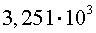
Здесь число 3,251 является мантиссой, а число 3 является порядком.
Стандартная форма записи числа часто используется в научных расчетах и очень удобна для сравнения чисел.
Для того, чтобы сравнить два числа, записанных в стандартной форме, нужно сначала сравнить их порядки. Большим будет то число, порядок которого больше. Если же порядки сравниваемых чисел одинаковы, то нужно сравнить мантиссы чисел. Большим в этом случае будет то число, у которого мантисса больше.
Например, если сравнить между собой записанные в стандартной форме числа
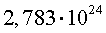
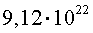
то, очевидно, первое число больше второго, поскольку у него порядок больше.
Если же сравнить между собой числа
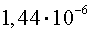
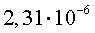
то, очевидно, что второе число больше, чем первое, поскольку порядки у этих чисел совпадают, а мантисса у второго числа больше.
Что такое мантисса
Содержание статьи
Значение мантиссы
Значение мантиссы в том, что по ней находится число, которое является источником логарифма. Целая часть показывает только степень десяти или тривиальный множитель, тогда как сама мантисса показывает, какое именно число должно быть умножено на тривиальный множитель, который имеет вид 0,001 или 100.
Экспоненциальная запись представляет это в следующем виде: N = M*n^p, где мантиссой является M. Для примера можно взять число 3600 и представить его в экспоненциальной записи. Получится следующее: 3600 = 3,6*10^3. Учитывая вышесказанное, мантиссой будет являться число 3,6.
Важно понимать, что число, имеющее плавающую запятую, также имеет изменяющуюся абсолютную точность и фиксированную относительную точность. Использование чисел с плавающей запятой лучше, чем представление чисел с фиксированной запятой, так как есть возможность применения большого диапазона значений, тогда как относительная точность не меняется. Это поможет понять следующий пример: форма, имеющая фиксированную запятую, позволяет представить число, которое занимает 2 разряда после запятой и 8 разрядов в целой части, в виде 8765,43; 123456,78 и так далее. Если же брать формат, имеющий плавающую запятую, можно произвести следующую запись: 1,2345678; 0,000012345678 и так далее. Однако для того, чтобы так сделать, важно иметь двухразрядное дополнительное поле, позволяющее записать показатели степени 10, начиная от 0 и кончая 1610. Общее число разрядов составит 10, то есть 8+2.
Мантисса, как для отрицательных, так и для положительных чисел, выражается в прямом коде. Различие в знаке будет отражено лишь в значении знакового разряда. Однако мантисса числа не может превышать единицы. Обычно точка в мантиссе располагается с левой стороны от старшего разряда. Для того, чтоб получить истинное значение числа, нужно умножить мантиссу на 16 в степени порядка. Порядок, полученный этим путем, называется характеристикой. Получается, что характеристика, которая отсчитывается от 64, будет всегда положительной.
В нормальной записи мантисса числа — всегда правильная дробь. Ее запись в ячейку производится так же, как запись числа с запятой в ячейку машины. Запятая фиксируется перед первым разрядом цифрового вида.
Мантисса числа, имеющая плавающую запятую, выражается шестнадцатеричными цифрами, при этом запятая располагается слева от самой высокой цифры мантиссы
Форма мантиссы
Есть две формы, позволяющие понять место применения мантиссы. Первая — нормальная форма числа. Эта форма, которая имеет мантиссу без учета знака на полуинтервале, то есть [0; 1) (0\le a
Числа с плавающей запятой
Плавающая запятая — форма представления действительных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто используемое представление утверждено в стандарте IEEE 754. Реализация математических операций с числами с плавающей запятой в вычислительных системах может быть как аппаратная, так и программная.
Содержание
«Плавающая запятая» и «плавающая точка»
Так как в некоторых, преимущественно англоязычных и англофицированных, странах (см. подробный список Decimal separator (англ.) ) при записи чисел целая часть отделяется от дробной точкой, то в терминологии этих стран фигурирует название «плавающая точка» (floating point (англ.) ). Так как в России целая часть числа от дробной традиционно отделяется запятой, то для обозначения того же понятия исторически используется термин «плавающая запятая», однако в настоящее время в русскоязычной литературе и технической документации можно встретить оба варианта.
Происхождение названия
Название «плавающая запятая» происходит от того, что запятая в позиционном представлении числа (десятичная запятая, или, для компьютеров, двоичная запятая — далее по тексту просто запятая) может быть помещена где угодно относительно цифр в строке. Это положение запятой указывается отдельно во внутреннем представлении. Таким образом, представление числа в форме с плавающей запятой может рассматриваться как компьютерная реализация экспоненциальной записи чисел.
Преимущество использования представления чисел в формате с плавающей запятой над представлением в формате с фиксированной запятой (и целыми числами) состоит в том, что можно использовать существенно больший диапазон значений при неизменной относительной точности. Например, в форме с фиксированной запятой число, занимающее 8 разрядов в целой части и 2 разряда после запятой, может быть представлено в виде 123456,78; 8765,43; 123,00 и так далее. В свою очередь, в формате с плавающей запятой (в тех же 8 разрядах) можно записать числа 1,2345678; 1234567,8; 0,000012345678; 12345678000000000 и так далее, но для этого необходимо двухразрядное дополнительное поле для записи показателей степени 10 от 0 до 1610, при этом общее число разрядов составит 8+2=10.
Скорость выполнения компьютером операций с числами, представленными в форме с плавающей запятой, измеряется в мегафлопcах (от англ. FLOPS — число операций с плавающей запятой в секунду ), гигафлопcах и так далее, и является одной из основных единиц измерения быстродействия вычислительных систем.
Структура числа
Число с плавающей запятой состоит из:
Нормальная форма и нормализованная форма
Использование в вычислительных машинах
В вычислительных машинах показатель степени принято отделять от мантиссы буквой «E» (exponent). Например, число 1,528535047×10 −25 в большинстве языков программирования высокого уровня записывается как 1.528535047E-25.
Краткий обзор
Существует несколько способов того, как строки из цифр могут представлять числа:
Запись числа в форме с плавающей запятой позволяет производить вычисления над широким диапазоном величин, сочетая фиксированное количество разрядов и точность. Например, в десятичной системе предоставления чисел с плавающей запятой (3 разряда) операцию умножения, которую мы бы записали как
в нормальной форме представляется в виде
(1,20×10 −1 ) × (1,20×10 −1 ) = (1,44×10 −2 ).
В формате с фиксированной запятой мы бы получили вынужденное округление
Мы потеряли крайний правый разряд числа, так как данный формат не позволяет запятой «плавать» по записи числа.
Диапазон чисел, представимых в формате с плавающей запятой
Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. На обычной 32-битной вычислительной машине, использующей двойную точность (64 бита), мантисса составляет 1 бит знак + 52 бита, показатель — 1 бит знак + 10 бит. Таким образом получаем диапазон точности примерно от 4,94×10 −324 до 1.79×10 308 (от 2 −52 × 2 −1022 до
1 × 2 1024 ). Пара значений показателя зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся значения NaN (Not a Number, не число) и +/-INF (Infinity, бесконечность), получающихся в результате операций типа деления на ноль нуля, положительных и отрицательных чисел. Также сюда попадают денормализованные числа, у которых мантисса меньше единицы. В специализированных устройствах (например GPU) поддержка специальных чисел часто отсутствует. Существуют программные пакеты, в которых объём памяти выделенный под мантиссу и показатель задаётся программно, и ограничивается лишь объёмом доступной памяти ЭВМ.
Машинная эпсилон
В отличие от чисел с фиксированной запятой, сетка чисел, которые способна отобразить арифметика с плавающей запятой, неравномерна: она более густая для чисел с малыми порядками и более редкая — для чисел с большими порядками. Но относительная погрешность записи чисел одинакова и для малых чисел, и для больших. Поэтому можно ввести понятие машинной эпсилон.
Машинной эпсилон называется наименьшее положительное число ε такое, что 


Разбираемся в числах с плавающей точкой (часть 0)
Здравствуйте, хабровчане. Я давно увлекаюсь темой регистров с плавающей точкой. Меня всегда волновало то, как происходит вывод на экран и т.д. Помню, давным-давно в универе реализовывал свой класс чисел с плавающей точкой, состоящих из 512 бит. Единственное, что я не мог никак реализовать — это вывод на экран.
Как только у меня появилось свободное время, я взялся за старое. Завел себе тетрадку и пошло-поехало. Хотелось додуматься до всего самому, лишь иногда заглядывая в стандарт IEEE 754.
И вот что из всего этого вышло. Интересующихся прошу под кат.
Чтобы освоить эту статью, надо знать следующее: что такое бит, двоичная система, арифметика на уровне знания отрицательных степеней. В статье не будут затронуты инженерные подробности реализации на уровне процессора а также нормализованные и денормализованные числа. Больший упор сделан на перевод числа в двоичную форму и наоборот, а также объяснение того, как вообще хранятся числа с плавающей точкой в виде битов.
Числа с плавающей точкой — очень мощный инструмент, которым надо уметь правильно пользоваться. Они не столь банальны, как целочисленные регистры, но и не столь сложны, если в них грамотно и потихоньку вникнуть.
В сегодняшней статье для примера я буду использовать 32-битные регистры. Числа с двойной точностью (64-битные) работают абсолютно по той же логике.
Сначала поговорим о том, как хранятся числа с плавающей точкой. Старший 31 бит у нас знаковый. Единичка значит, что число отрицательное, а ноль, соответственно наоборот. Далее идут 8 бит экспоненты. Эти 8 битов представляют из себя обычное беззнаковое число. И в самом конце идут 23 бита мантиссы. Для удобства будем обозначать знак как S, экспоненту как E, а мантиссу, как ни странно, M.
Получаем общую формулу
У мантиссы принято считать один неявный единичный бит. То есть мантисса будет представлять из себя 24 бита, но так как старший 23-й бит всегда единица, то его можно не записывать. Таким образом это «ограничение» будет давать нам единственность представления любого числа.
Мантисса из себя представляет обычное двоичное число, но в отличие от целых чисел, старший бит это 2^0 степени и далее по убыванию степеней. Вот тут и пригождается экспонента. В зависимости от ее значения, степень двойки старшего бита увеличивается либо уменьшается. Вот и вся гениальность этой задумки.
Давайте попробуем показать это на наглядном примере:
Представим число 3.625 в двоичном виде. Поначалу разобьем это число на степени двойки.
Степень старшей двойки равна единице. E – 127 = 1. E = 128.
0 1000000 11010000000000000000000
Вот и все наше число.
Попробуем также и в обратную сторону. Пусть у нас есть 32 бита, произвольные 32 бита.
0 10000100 (1)11011100101000000000000
В скобочках указан тот самый неявный старший бит.
Сначала вычислим экспоненту. E = 132. Соответственно степень старшей двойки будет равна 5. Итого имеем следующее число:
Нетрудно догадаться, что мы можем хранить всего лишь диапазон из 24-х степеней двойки. Соответственно, если два числа отличаются в экспоненте на больше чем 24, то при сложении число остается равным большему среди них.
Для удобной конвертации я накидал небольшую программу на языке C.
Шагом сетки является минимальная разницу между двумя соседними числами с плавающей точкой. Если представить последовательность битов такого числа как обычное целое число, то соседнее число с плавающей точкой будет отличаться в битах как целое число на единицу.
Можно выразиться иначе. Два соседних числа с плавающей точкой будут отличаться на 2 ^ (E — 127 — 23). То есть на разницу, равную значению младшего бита.
В качестве доказательства можете поменять main в коде и скомпилировать еще раз.
Думаю на сегодня можно закругляться, а то получается слишком длинно. В следующий раз буду писать о сложении чисел с плавающей точкой и потере точности при округлении.

