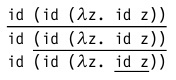что такое лямбда в термодинамике
Краткая история Лямбды, или почему Итан привирает
Пронаблюдав за удалёнными сверхновыми и измерив, как Вселенная расширялась миллиарды лет, астрономы обнаружили нечто удивительное, загадочное и неожиданное.
By observing distant supernovae and measuring how the Universe had expanded over billions of years, astronomers discovered something remarkable, puzzling and entirely unexpected
О какой неожиданности может идти речь? Там ведь совершенно шикарная история длиной в 80 лет с яркими открытиями и закрытиями. История про то, как на самом деле делается настоящая наука. История скорее про физиков, чем про физику.
О чём вообще весь сыр-бор?
Первую версию Общей Теории Относительности (ОТО) Альберт Эйнштейн представил публике 25 ноября 1915 года. В оригинале уравнения ОТО Эйнштейна выглядели вот так:
или, в современной записи, вот так:
Для неумеющего в тензоры читателя понятнее уравнение (1) в оригинальной записи Эйнштейна. Там написано, что энергия-импульс материи G равен кривизне пространства R плюс тензор Риччи S. (Этот самый тензор Риччи тоже есть кривизна, только в более другой форме).
Сейчас, решая уравнение ОТО, энергию-импульс обычно считают известным, а ищут как раз кривизну. Поэтому в современной записи стороны уравнения поменяли местами. Заодно поменяли буковки: G → T, S → Rμν.
Откуда есть пошла лямбда
Одним из первых серьёзных математиков, который занялся проверкой выкладок Эйнштейна, стал Эли Жозеф Картан (не путать с его сыном Анри, тоже известным математиком).
Картан-папа нашёл у Эйнштейна ряд технических ошибок, в частности, такую, которая современному поколению ЕГЭ известна под кодовым названием «потерять константу при интегрировании». Сегодня эту потерянную константу обозначают заглавной греческой буквой лямбда, Λ.
Но физика — это вам не математика. Здесь нельзя взять формулу и напихать в неё добавочных слагаемых просто так. Нужно иметь очень веские основания, и теоретические, и экспериментальные.
Хотя ниже вы увидите, насколько мало Эйнштейн знал о Вселенной в те годы, но тогда, в 1916, такие основания у него были. Альберт Германович точно знал, что звёзды не попадали друг на друга и совершенно не собираются этого делать в обозримом будущем. Однако, в ОТО-1915 было только притяжение, которое нужно было чем-то сбалансировать.
Вводимая в уравнения лямбда как раз отвечала за отталкивание. Поэтому в 1917 Эйнштейн опубликовал «дополненную и улучшенную» версию ОТО с космологической постоянной Λ. В современной записи уравнение выглядит так:
Первое физическое толкование смысла лямбды
Возьмём уравнение ОТО-1917 и вынесем за скобки метрический тензор . Тогда внутри скобок у нас останется выражение (R/2 — Λ). Здесь R без индексов — это обычная, «школьная» скалярная кривизна. Если на пальцах — это число, обратное радиусу окружности/сферы. Плоскому пространству соответствует R = 0.
В такой трактовке ненулевое значение Λ означает, что наша Вселенная искривлена сама по себе, в том числе и при отсутствии какой-либо гравитации. Ну, вот такой нам достался мир. Однако, большинство физиков в это не верят, и считают, что у наблюдаемого искривления должна быть какая-то внутренняя причина. Какая-то неведомая доселе фигня, которую можно открыть.
На сегодняшний день измеренная кривизна пространства Вселенной таки равна нулю, но с очень паршивой точностью, порядка 0.4%. И не очень-то видно способов эту точность улучшить.
С измерениями кривизны есть две концептуальные проблемы.
Первая в том, что мы не можем измерить совсем пустое пространство, потому что просто ничего там не видим. А если там есть что-то, что мы таки видим, то пространство уже не пустое и, значит, уже дополнительно искривлено гравитацией.
Вторая проблема сложнее и носит персональное название «проблема систем отсчёта». Смысл там вот в чём.
Допустим, у нас есть как-то измеренные координаты объектов, плюс пачка фотографий этих объектов в разных ракурсах (снятых из разных точек). Тогда мы можем вычислить кривизну пространства. Например, гравитация Солнца отклоняет пролетающий мимо свет далёких звёзд. Во время солнечных затмений это отклонение можно измерить экспериментально и сравнить с предсказаниями ОТО.
Теперь наоборот: допустим, мы знаем кривизну пространства, и у нас есть пачка фотографий. Тогда, если кривизна достаточно хорошая, без чёрных дыр и т.п. — мы можем вычислить координаты объектов на фото. Именно так работают наши глаза, точнее мозги, когда вычисляют расстояние до объектов по двум фоткам с разных точек.
Но вот для далёких галактик всё плохо. Мы не знаем их точных координат. И кривизну пространства на больших масштабах мы тоже не знаем. И даже пачки фотографий у нас нет: на таких масштабах можно считать, что все они сделаны практически из одной точки. Поэтому за пределами Млечного Пути мы не можем быть уверены ни в координатах, ни в кривизне.
И в силу универсальности гравитации это касается не только собственно «фотографий», но абсолютно любых измерений удалённых объектов.
Поэтому измерить кривизну наблюдаемой Вселенной в целом мы можем только из очень окольных соображений.
Вселенная Фридмана
Meanwhile in Russia, не смотря на войны и революции, над теорией ОТО бился прапорщик (и по совместительству профессор) Александр Александрович Фридман. Он рассмотрел все варианты лямбд и выяснил следующее:
При Λ 0 на больших расстояниях заруливает геометрия, а звёзды и галактики ускоренно разлетаются «с горки» (вариант Эйнштейна-1917). При достаточно большой лямбде на небе может вообще ни остаться ни одной звезды кроме Солнца, при умеренном значении — останется только наша галактика, слившаяся с ближайшими соседями.
Но самое интересное происходит при Λ = 0. Здесь всё зависит от начальных условий — т.е. координат и скоростей конкретных галактик. Возможны три варианта: большое сжатие, большой разлёт и стационарный вариант, когда галактики разлетаются, но с относительно небольшими скоростями и без ускорения.
Сегодня вышеописанные ситуации называются космологическими решениями Фридмана.
Статьи Фридмана 1922 и 1924 годов отменяли необходимость в лямбда-члене, из-за чего поначалу были приняты Эйнштейном в штыки.
За свою работу Фридман вполне мог претендовать на Нобелевку.
Из решений Фридмана вытекало, что у Вселенной может быть начало. Эту идею подхватили многие физики, а возглавил то, что позже назвали «теорией Большого Взрыва», русско-американец Георгий Гамов, полагавший Λ = 0.
И да, статья Итана про примерно такой график (конкретно на этом учтены данные на 2010 год):

Здесь по горизонтали отложено z — это красное смещение, по вертикали наблюдаемая яркость сверхновых особого типа Ia, которые всегда выделяют одно и то же количество энергии. Вообще, это два способа измерения одного и того же расстояния, но, так сказать, в разные моменты времени.
Серые палки — наблюдавшиеся события с их погрешностью измерений. Синим пунктиром отложено предсказание при Λ = 0, красной линией — аппроксимация фактически наблюдаемых значений. Отклонение красной линии от прямой означает, что Вселенная расширяется ускоренно. Но Эйнштейн об этом так и не узнал.
Вселенная Каптейна
Перейдём к экспериментальной части.
Голландский астроном Якобус Корнелиус Каптейн открыл звезду Каптейна в 1897, после чего приступил к opus magnum всей своей жизни. Объединяя огромное количество наблюдений разных обсерваторий, он попытался создать первую карту Вселенной. По его карте выходило, что вселенная имеет форму вращающегося (sic!) диска крышесносящего по тем временам размера 40000 световых лет, причём Солнце находится отнюдь не в центре, а вполне себе на задворках. Закончена и опубликована эта работа была только в 1922.
Для понимания уровня тогдашних знаний: то, что Каптейн считал невероятно огромной Вселенной, сегодня считается совершенно рядовой, ничем не примечательной среди миллиардов таких же… галактикой Млечный Путь. Тем не менее, заслуга Каптейна в том, что он открыл её вращение и приблизительно вычислил её центр.
Наблюдения Хаббла (астронома, а не телескопа)
Если говорить про астрономов, то больше всех для истории лямбды сделал Эдвин Хаббл. Он чувствовал, что с туманностями что-то не так, и в 1922 предположил, что часть из них — не облака газа, а очень удалённые объекты. Проверяя свою теорию, в 1924 он первым в мире разглядел отдельные звёзды в туманности Андромеды (да, ему всю жизнь везло на очень хорошие телескопы. И после смерти — продолжило везти). Именно Хаббл предложил термин «галактика» — собственно, это «млечный путь» по-гречески.
Статью со своими открытиями, из которой следовало, что Вселенная значительно больше, чем наш Млечный путь, Хаббл представил американскому астрономическому обществу первого января 1925. За что и был освистан страдающими от похмелья коллегами, едва свыкшимися с расстояниями Каптейна.
Хаббл не унимался и прикрутил к телескопу ещё и спектрометр. Анализируя красное смещение галактик, он выяснил, что галактики разбегаются, а Вселенная, соответственно, расширяется. Заодно он открыл закон имени себя с константой имени себя (впрочем, закон был предсказан Леметром), и описал всё это в статьях к концу 20-ых годов. Согласно его наблюдениям, оказалась верна модель Фридмана для Λ = 0.
Это выбило из-под лямбды теперь уже и экспериментальные основания её существования.
Эйнштейн, гляда на это, оперативно вычеркнул космологическую постоянную из уравнений ОТО, а в конце жизни считал историю с лямбдой «самой большой своей ошибкой».
Так что, кроме всех своих открытий, Хаббл также невольно «закрыл» лямбду. На целых 70 лет.
Здесь ещё нужно упомянуть, что первоначальные оценки Хаббла были очень уж неточными и показывали возраст Вселенной порядка 2 миллиардов лет. Позднее это войдёт в противоречие с данными геофизиков, которые при помощи радиоизотопного анализа оценят возраст Земли в несколько миллиардов лет, и десятилетиями будет сильнейшей головной болью для физиков-космологов.
Стационарная Вселенная Хойла
С начала 30-ых годов вопрос с лямбдой считался решённым, и из мейнстримных физиков ей никто толком не занимался. Одним из редких исключений, рискнувших попереть супротив самого Эйнштейна, стал британец Фред Хойл.
Речь пойдёт о гелии. Этот элемент феноменально инертен и не хочет ни с чем реагировать. Причём не только химически, но и физически тоже, если мы говорим про гелий-4. Его ядро — альфа частица — имеет пиковую энергию связи на нуклон в своей области. см. рис из какого-то реферата:
Это значит, что альфа-частица не может присоединить дополнительные протоны или другую альфа-частицу иначе как случайно: это просто-напросто энергетически невыгодно. А в ядрах звёзд ничего кроме протонов и альфа-частиц и нет.
Возникал резонный вопрос: а откуда, собственно, взялись химические элементы тяжелее гелия?
Ближайшее ядро, в которое может превращаться гелий-4, это углерод-12. Но для этого нужно объединить три альфа-частицы.
Проблема в том, что вероятность столкновения трёх альфа-частиц одновременно слишком мала. А двухшаговый процесс (сначала сталкиваются две частицы, потом очень быстро, пока они не разлетелись обратно на две альфа-частицы, в них врезается ещё одна), в принципе, возможен, но расчёты Эдвина Солпитера показывали, что такой процесс идёт слишком вяло, чтобы производить существенные количества углерода.
И вот весной 1953 года в Калтех приехал британец Фред Хойл, тогда ещё без приставки «сэр», и сразу отправился к местному завлабу Уильяму Фаулеру.
Там он с порога спросил: может ли углерод-12 обладать энергетическим уровнем, равным 7,69 МэВ? Фаулер сначала подумал, что к нему припёрся очередной сумасшедший, но решил спросить — «вообще-то нет, а вам, собственно, зачем?» На что Хойл ответил: ну, я же существую, значит, у ядра углерода должен быть такой энергетический уровень. Отличная аргументация!
Однако, по расчётам Хойла выходило, что при наличии такого уровня в три-альфа процессе наступает резонанс, и звёзды — красные гиганты производят достаточно много углерода для нашего существования.
Удивительно, но американцы решили провести небольшой эксперимент на своём ускорителе. И да — триумфально нашли нужный энергетический уровень на 7.65 МэВ, который физики-ядерщики всего мира почему-то проглядели во всех предыдущих экспериментах.
Сегодня такое возбуждённое состояние углерода-12, когда три альфа-частицы фактически выстраиваются по линии, называется хойловским. Соответствующая статья Хойла, Фаулера и супругов-астрономов Джефри и Маргерит Бёрбиджей является краеугольным камнем современных теорий звёздного нуклеосинтеза и настолько часто цитируется, что обозначается просто B²FH, без ссылок и расшифровок.
И — да, на сегодня это чуть ли не единственное известное успешное предсказание на основе антропного принципа.
Хойл был вполне авторитетным учёным в области космологии, причём, в отличие от многих коллег, так сказать «прикладной», т.е. относительно просто проверяемой, космологии. Именно он объяснил, как из однородных разреженных облаков газа путём гравитационного сжатия образуются звёзды и галактики. Также именно Хойл придумал название «Большой взрыв», причём использовал это название в ругательном смысле.
Хойлу и его соавторам — Бонди и Голду — очень не нравился «большой хлопок» (более корректный перевод фразы big bang), при котором у Вселенной есть начало. Они считали, что так же, как равноправны все точки пространства, должны быть равноправны и все точки во времени. У такой Вселенной нет ни начала, ни конца, и при этом она постоянно, хотя и очень медленно расширяется.
Однако, из квантовых флуктуаций постоянно рождается новое вещество, причём так, что средняя плотность материи остаётся одинаковой. Расчёты показывают, что в одном кубическом километре пространства должен рождаться всего-навсего один протон раз в 300000 лет (а так же один электрон или что-то типа того для сохранения электрического заряда). Прекрасное число, чтобы исключить любую возможность какой-либо экспериментальной проверки!
Теория стационарной Вселенной серьёзно рассматривалась как альтернатива теории Большого Взрыва в 50-х и начале 60-х. Но экспериментальное открытие в 1964 году предсказанного ТББ реликтового излучения поставило на ней крест.
Хойл, впрочем, не унимался и совершенствовал свою теорию до самого выхода на пенсию. Последняя редакция, разработанная на пару с его другом Джефри Бёрбиджем в 1993, так называемая «квази-стационарная Вселенная», предполагает локальные мини-взрывы и объясняет примерно все наблюдаемые факты, но какой-либо популярностью не пользуется. И да, она подозрительно похожа на общепринятую на сегодня теорию инфляции (но отличается знаками плюс-минус в некоторых местах).
За статью B²FH дали Нобелевку. Но только Фаулеру, который распорядился провести десятидневный эксперимент. Ни супругам Бёрбиджам, проводившим длительные астрономические наблюдения и собственно написавшим статью, ни автору идеи Хойлу нобелевку не дали — за упорствование в космологической ереси.
Самое интересное, что Хойл дожил до экспериментального подтверждения ускоренного разбегания галактик в 1998. Но даже это не стало поводом для нобелевского комитета исправить очевидную ошибку.
Квантовая лямбда
Вернёмся к уравнению ОТО.
Слева (в современной записи) стоит кривизна пространства, сиречь гравитация по ОТО. Справа — тензор энергии-импульса. Под этим тензором стоит жутко сложный матан, но суть в следующем: там учтена вся-вся-вся материя Вселенной во всех видах и состояниях. И обычное вещество, и всякие хитрые частицы, и все виды излучений (кроме гравитации, которая слева).
Теперь мысленно перенесём лямбду вправо. В такой записи это будет не дополнительная кривизна, а какая-то неучтённая энергия (замечу, отрицательная, раз уж мы считаем лямбду положительной). И здесь просматриваются две возможности.
Первая гипотеза состоит в том, что лямбда — это энергия собственно вакуума. Звучит диковато, но на самом деле вполне согласуется с квантовой механикой. Возьмём кусок пространства и уберём из него всё, что хотя бы в принципе можно убрать. Уберём всё вещество, все частицы и все волны, независимо от их природы. Останутся только физические поля в невозмущённом состоянии. Полный штиль.
Так вот, у некоторых полей (например, Хиггсовских) в пустоте ненулевое значение. И теоретически у них есть некоторая энергия. Кроме того, в силу принципа неопределённости у любых полей есть квантовые флуктуации — и они тоже имеют некоторую энергию.
Возникает, правда, маленькая техническая проблемка. Если всё аккуратно посчитать, расчётный результат отличается от наблюдаемого на 120 — нет, не раз, на 120 порядков. В 100 миллиардов миллиардов гуглов раз! Это по праву считается «худшим предсказанием в истории теоретической физики».
Вторая возможность: физики всё-таки забыли что-то посчитать, когда вычисляли тензор энергии-импульса. Это «что-то» должно быть весьма странным (давать отрицательное давление), ничего похожего мы пока не знаем, так что тут скорее ситуация «не знал — не знал, и забыл». Сейчас это «что-то» называется «тёмная энергия», и этой энергии должно быть примерно в два раза больше, чем энергии у обычной и тёмной материи вместе взятых. ← современная физика находится здесь.
Вместо заключения
Звоночки о ненулевом значении лямбды начали появляться на рубеже 90-ых — из точных измерений реликтового излучения и т.д., и к 1997 превратились в набат. Совсем неудивительно, что сразу две группы физиков вооружились современными инструментами и бросились перепроверять дедушку Хаббла. Поэтому, когда Итан пишет про «совершенно неожиданно», он, мягко говоря, привирает.
И пока для объяснения лямбды у нас нет ничего лучше «тёмной энергии», эта история будет продолжаться.
λ-исчисление. Часть первая: история и теория
Идею, короткий план и ссылки на основные источники для этой статьи мне подал хабраюзер z6Dabrata, за что ему огромнейшее спасибо.
UPD: в текст внесены некоторые изменения с целью сделать его более понятным. Смысловая составляющая осталась прежней.
Вступление
Возможно, у этой системы найдутся приложения не только
в роли логического исчисления. (Алонзо Чёрч, 1932)
Вообще говоря, лямбда-исчисление не относится к предметам, которые «должен знать каждый уважающий себя программист». Это такая теоретическая штука, изучение которой необходимо, когда вы собираетесь заняться исследованием систем типов или хотите создать свой функциональный язык программирования. Тем не менее, если у вас есть желание разобраться в том, что лежит в основе Haskell, ML и им подобных, «сдвинуть точку сборки» на написание кода или просто расширить свой кругозор, то прошу под кат.
Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.
Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…
λ-исчисление: основные понятия
Синтаксис
В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции, только хардкор. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.
Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.
Процесс вычисления
Рассмотрим следующий терм-применение:
Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:
который для простоты можно переписать как
(напомним, что id — это функция тождества вида λx.x )
В этом терме содержится три редекса:
Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение
(λx.λy. x) z ((λx.x x)(λx.x x))
Этот терм имеет нормальную форму z несмотря на то, что его второй аргумент такой формой не обладает. На её-то вычислении и зависнет стратегия вызова по значению, в то время как стратегия вызова по имени начнёт с самого внешнего терма и там определит, что второй аргумент не нужен в принципе. Вывод: если у редекса есть нормальная форма, то «ленивая» стратегия её обязательно найдёт.
На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.
Объяснение лямбда-выражений
У меня возникли вопросы о лямбда-выражениях и RxJava. Эти вопросы в основном касаются не полного понимания лямбда-выражений или RxJava. Я попытаюсь объяснить лямбда-выражения как можно проще. RxJava я опишу отдельно.
Лямбда-выражения и RxJava
Что такое лямбда-выражения? Лямбда-выражения – это «всего лишь» новый способ сделать то же самое, что мы всегда могли сделать, но в более чистом и менее многословном новом способе использования анонимных внутренних классов.
Анонимный внутренний класс в Java – это класс без имени, он должен использоваться, если вам необходимо переопределить методы класса или интерфейса. Анонимный внутренний класс может быть создан из класса или интерфейса.
В Android мы обычно используем анонимный внутренний класс в качестве слушателя, например, для кнопок такого рода:
Вернемся к лямбда-выражениям. Это следующая часть, которая является частью предыдущего кода, который считается анонимным внутренним классом.
Лямбда-выражения могут использоваться только в том случае, если вам нужно переопределить не более одного метода. К счастью для нас, View.OnClickListener содержит только один. Посмотрите на код ниже. Как думаете, какую его часть нам придётся убрать?
В некоторых случаях вам может потребоваться добавить тип к параметру, если компилятору не удается его угадать, вы можете сделать это, добавив его перед параметром:
Вы также можете использовать многострочный код:
Если у вас есть интерфейс с методом, принимающим два параметра…
…лямбда-выражение будет выглядеть следующим образом:
Если метод имеет возвращаемый тип…
…лямбда-выражение будет выглядеть следующим образом:
Но это еще не все, есть некоторые специальные случаи, которые делают код еще меньше. Если тело вашего метода содержит только одну строку кода, вы можете удалить фигурные скобки <>. Если вы удаляете фигурные скобки, вам также необходимо удалить точку с запятой, оставив следующее:
Есть еще одна вещь, которую мы можем сделать. Если у нас только одна строка кода, то компилятор может понять, нужна ли возвращаемая часть или нет, поэтому мы можем оставить ее следующим образом:
Если бы у нас был многострочный код, это свелось бы к следующему:
Так что же мы сделали? Мы взяли это:
и превратили вот в это:
Осталось только одна вещь, ссылки на методы. Допустим, у нас есть интерфейс, как и раньше, и метод, который этот интерфейс принимает как параметр:
Без лямбда-выражения это выглядело бы так:
Добавив лямбда-выражение, как мы это делали раньше, получим следующее:
Но это еще не все. Если используемый код – однострочный и вызываемая функция принимает один параметр, мы можем передавать ссылку на метод в таком виде:
Параметр будет передаваться автоматически, без необходимости использования другого кода! Удивительно, правда? Надеюсь, вы узнали что-то новое!