что такое линейный график
Линейная функция, ее свойства и график
теория по математике 📈 функции
Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.
Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.
Число k называется угловым коэффициентом прямой.
Свойства линейной функции
Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.
Пример №1
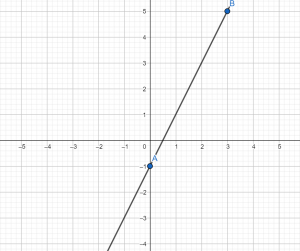
Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:
Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).
Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:
Вписываем в таблицу значения у:
Теперь строим систему координат, отмечаем в ней точки с координатами А(0; –1) и В(3;5), проводим через эти две точки прямую.
Итак, по формуле мы видим, что угловой коэффициент — положительный, значит, график – возрастает, что мы и видим на нашем графике.
Пример №2.
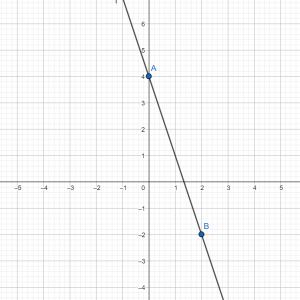
Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.
По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).
Пример №3
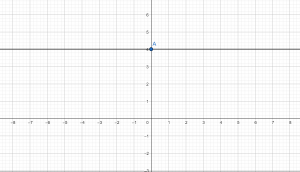
Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:
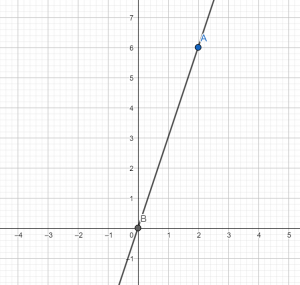
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ассмотрим коэффициенты под №3. Если k 90 0 ) угол с положит.направлением оси абсцисс (Ох). Если b 0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом ( 0 ). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b 0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
График данной функции зависит от k и b.
pазбирался: Даниил Романович | обсудить разбор | оценить
График линейной функции (ЕГЭ 2022)
Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое линейная функция.
Начнем с небольшой проверки:
Если хоть один вопрос вызвал затруднения, прочти тему «Линейная функция».
Приступим к покорению линий и графиков!
График линейной функции — коротко о главном
График линейной функции – прямая линия. Прямую можно провести через две точки.
Чтобы построить график линейной функции вида y=kx+b, нужно:
Рассмотрим пример для функции \( y=2x+1\):
Проще всего найти функцию, если аргумент: \( x=0:y\left( 0 \right)=2\cdot 0+1=1\).
Итак, первая точка имеет координаты \( \left( 0;1 \right)\).
Теперь возьмем любое другое число в качестве \( x\), например, \( x=1:y\left( 1 \right)=2\cdot 1+1=3\).
Вторая точка имеет координаты \( \left( 1;3 \right)\).
Угловой коэффициент \( \displaystyle k\) – это тангенс угла наклона прямой.
Для его нахождения выберем две точки \( \displaystyle A\) и \( \displaystyle B\) на графике и построим прямоугольный треугольник с гипотенузой \( \displaystyle AB\)
\( \displaystyle k=tg\alpha =\frac
Построение графика линейной функции
Итак, ты уже умеешь обращаться с линейной функцией, анализировать ее график и строить его по точкам. Кстати, сколько нужно точек, чтобы построить график линейной функции?
Скажу сразу, эта тема настолько простая, что много нового ты здесь не выучишь. Но ты научишься не теряться во всяких нестандартных ситуациях.
Итак, дамы и господа, линейная функция:
Построение графика линейной функции: ты берешь два каких-либо икса, (например, \( \displaystyle 0\) и \( \displaystyle 1\)), подставляешь их в формулу, находишь соответствующие игреки.
Затем отмечаешь эти две точки на координатной плоскости, прикладываешь линейку, и график готов. Просто и быстро, и ничего выдумывать не надо.
Но бывает, что функция задана по-другому, например, неявно. Сейчас разберем, как быстро справляться с такими ситуациями.
Пример неявно заданной линейной функции
Постройте график уравнения \( \displaystyle 2y+3x=6\).
Ну а что тут сложного? Чтобы произвести построение графика линейной функции выражаем y и строим по точкам.
Это да, но можно сделать проще и интересней!
Выясним, в какой точке эта прямая будет пересекать ось \( \displaystyle Ox\).
Что характерно для этой точке? Правильно, \( \displaystyle y=0\). Так и пишем:
\( \displaystyle 2\cdot 0+3x=6\text< >\Rightarrow \text< >x=2\)
А теперь проделаем то же самое с другой осью: в какой точке график пересекает ось \( \displaystyle Oy\)?
\( \displaystyle x=0\text< >\Rightarrow \text< >2y+3\cdot 0=6\text< >\Rightarrow \text< >y=3\)
Бум! Вот и они – две точки графика. Осталось только приложить линейку:
Согласись, это было быстро и просто!
А теперь сам:
Ладно, а как еще можно задать функцию?
Ну, например словесно:
Прямая проходит через точку \( \displaystyle A\left( 2;3 \right)\), а ее угловой коэффициент равен \( \displaystyle 0,75\).
Ну что же, вспоминаем: что такое угловой коэффициент?
Что такое угловой коэффициент
Это, с одной стороны, коэффициент при \( \displaystyle x\), а с другой – это тангенс угла между прямой и осью \( \displaystyle Ox\).
Вот это мы и используем когда делаем построение графика линейной функции: ставим точку \( \displaystyle A\), и рисуем прямоугольный треугольник так, что один его катет параллелен оси \( \displaystyle Ox\), а другой – перпендикулярен.
При этом второй катет должен быть ровно в \( \displaystyle 0,75\) раз больше первого.
Очень удобно в этом случае, чтобы первый катет был равен \( \displaystyle 4\), тогда второй будет равен \( \displaystyle 3\):
4 примера построения графика линейных функций
Пример №1
Прямая, уравнение которой имеет вид \( y=-2x+b\) (\( b\) неизвестно), проходит через точку \( M\left( 1;2 \right)\). Постройте ее.
Должно получиться вот так:
Пример №2
Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку \( A\left( 3;1 \right)\) и параллельной прямой \( y=-1,5x+1\).
Строить график прямой \( y=-1,5x+1\) нельзя.
О, это что-то новенькое. Про параллельность прямых мы еще не учили.
Но как обычно, все просто. Нарисуем несколько параллельных прямых на координатной плоскости:
Что у них общего? Вообще, какие параметры важны для графиков? Конечно же, коэффициенты \( k\) и \( b\).
И сразу становится ясно: раз \( k\) отвечает за наклон, а наклон у них одинаковый (это же параллельные прямые, а ось \( Ox\) – секущая), значит, у них одинаковый коэффициент \( k\)!
Вернемся к задаче. Напомню условие:
Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку \( A\left( 3;1 \right)\) и параллельной прямой \( y=-1,5x+1\).
График
Опубликовано 27.06.2021 · Обновлено 27.06.2021
Что такое График?
Линейный график – это графическое представление исторического движения цены актива, которое соединяет ряд точек данных непрерывной линией. Это самый простой тип графиков, используемых в финансах, и обычно он отображает только цены закрытия ценных бумаг с течением времени. Линейные графики можно использовать на любом таймфрейме, но чаще всего с ежедневными изменениями цен.
Ключевые моменты
Пример линейной диаграммы
Объяснение линейных диаграмм
Линейный график дает трейдерам четкое представление о том, куда изменилась цена ценной бумаги за определенный период времени. Поскольку линейные графики показывают только цены закрытия, они уменьшают шум от менее критических моментов торгового дня, таких как открытие, максимум и минимум. Поскольку цены закрытия обычно считаются наиболее важными, понятно, почему линейные графики популярны среди инвесторов и трейдеров. К другим популярным стилям диаграмм относятся гистограммы, свечные диаграммы и точечные и фигурные диаграммы. Трейдеры могут использовать линейные графики с другими графиками, чтобы увидеть полную техническую картину.
Преимущества использования линейных графиков
Простота в использовании : линейные графики идеально подходят для использования начинающими трейдерами из-за своей простоты. Они помогают научить базовым навыкам чтения графиков, прежде чем изучать более продвинутые методы, такие как чтение японских свечей или изучение основ точечных и фигурных графиков. Объем и скользящие средние можно легко применить к линейному графику, пока трейдеры продолжают свое обучение.
Ограничения использования линейных графиков
Как визуализировать данные: типы графиков
Редактор Наталия Шергина специально для блога Нетологии адаптировала статью об эффективных способах визуализации данных.
Предположим, вы понимаете важность визуального представления данных, знаете, какие навыки для этого нужны и, более того, обладаете ими. Заодно представим, что у вас есть данные для визуализации, осталось только разобраться, какие виды графиков и диаграмм подойдут. В статье мы расскажем о самых эффективных способах визуализации данных — вам будет из чего выбрать.
Столбчатая диаграмма (Bar Graph)
Скорее всего, это был первый способ визуализации, с которым вы столкнулись. Вспомните школьные учебники, таких диаграмм там было много. Если вы думали, что столбчатые диаграммы вместе со школой остались позади — не спешите с ними прощаться. Многие виды данных удобно представлять с их помощью: информацию о пробках на дороге, увеличение клиентской базы, график продаж. Столбчатые диаграммы — один из самых наглядных видов представления статистики.
Линейная диаграмма (Line Chart)
Этот вид графиков напоминает вершины горного хребта, и это сравнение неслучайно. С помощью линейных диаграмм можно графически представить горы данных и извлечь столько же инсайтов. Подходят для представления колебаний акций, темпа роста компании, построения прибыльной системы.
Гистограмма с несколькими осями (Multi-Axis Charts)
Это сочетание столбчатой диаграммы и линейного графика. Подойдёт, если нужно представить два или более фактора для выявления параллелей или сравнения. Гистограммы с осями часто используют на заседании членов советов компании, чтобы сопоставить, например, рыночную цену и общую выручку.
Гистограмма (Bar Histograms)
Ещё один график из школьных учебников. Гистограммы используют для представления числовых данных одной категории и их изменения с течением времени. Пример — изменение численности населения страны за конкретный период.
Как и столбчатые диаграммы, гистограммы состоят из столбцов. Поэтому эти два вида графиков часто путают. Давайте разбираться.
Круговая диаграмма (Pie Charts)
Кто работал с Экселем, тот наверняка знаком с круговыми диаграммами. Поставил её — и отчёт сразу выглядит презентабельнее, так? А если серьёзно, то круговые диаграммы — это отличный способ представить части одного целого. Например, долю компании на рынке, ваш вклад в общий проект или разработку секторов для инвестиционного плана.
Каждому из нас приходилось работать хотя бы с одной из перечисленных диаграмм. А если нет, то их названия вы точно слышали. На этом мейнстрим заканчивается. Далее — менее популярные графики.
Диаграмма спагетти (Spaghetti Charts)
К сожалению, это не совсем о еде. Диаграмма спагетти — очень необычный вид графиков, который только набирает популярность. Здесь без визуальной подсказки не объяснишь.
Помимо метеорологии, эти диаграммы подходят для визуализации взаимосвязей, что особенно полезно в юридических и судебных вопросах.
Географическая диаграмма (Map Charts)
Географические диаграммы специально разработаны для анализа географической информации, представления пространственных отношений и региональных данных. Используйте их, если нужно графически изобразить глобальную клиентуру, план расширения компании или план диверсификации производства. Эти диаграммы покажут, какие географические области развиваются, а каким нужно больше внимания. Также они помогают принимать решение — например, куда инвестировать или какие страны лучше для жизни.
Стрим-график или график потока (Stream Graph)
Даже если вы ни разу не видели землетрясения, то о сейсмографе слышали наверняка. Это машина, которая реагирует на сейсмическую активность и записывает сейсмоволны в виде графика.
Сейсмограф фиксирует толчки 24 часа 7 дней в неделю. Данные представляются графически в виде «потока» или «волн» вдоль центральной оси. Сейсмография — не единственная сфера применения графиков потока. Они особенно эффективны для графического изображения изменений за период времени.
Пузырьковая диаграмма (Bubble Charts)
Не очень серьёзное название, но суть не в нём. Сфера применения таких диаграмм в представлении и анализе данных огромна. Если говорить технически, пузырьковая диаграмма пригодится для визуализации анализа взаимодействий и распределения. А проще говоря, информация представлена в трёх измерениях или плоскостях. Допустим, у вас три вида данных: общее количество товаров, число каждого проданного продукта и выручка от продаж каждого продукта. Если вы хотите видеть взаимосвязь этих данных на одном графике, то пузырьковая диаграмма для вас.
Лучевая диаграмма (Sunburts)
Любители интернет-магазинов, эта информация для вас. Ваше поведение на сайте и то, на какие страницы вы заходите, заносится в историю, а админы магазинов могут легко представить эту информацию в виде лучевой диаграммы, чтобы понять, куда идёт основной трафик на сайте и какие страницы посещают реже всего. Такие диаграммы идеальны для представления иерархических данных.
Полярные часы (Polar Clock)
Ещё один интересный, но пока не самый популярный вид представления данных. График работает по принципу часов и каждую секунду показывает количество проделанной работы. Похоже на окно «копирование файлов», где зелёный индикатор показывал, сколько процентов данных уже скопировано. Представьте себе то же самое, только в форме круга — это и есть диаграмма полярные часы.
Интерактивная кольцевая диаграмма (Donut Transitions)
Это та же кольцевая диаграмма, только анимированная. Интерактивная кольцевая диаграмма — один из лучших способов для выявления закономерностей между несколькими параметрами. Эффективна для представления части целого и анализа зависимости величин. При изменении анализируемых параметров изменяются и пропорции диаграммы. Пригодится тем, кто следит за динамикой изменения — например, изменения стоимости акций в результате каких-либо действий компании.

Инфографика
Это одни из наиболее эффективных способов визуализации данных. Какие-то из них более привычны, о других пока мало кто знает. Новые виды графиков и диаграмм появляются вместе с новыми видами данных, что происходит непрерывно. Это значит, что скоро появятся более продвинутые способы визуализации.

Мнение автора и редакции может не совпадать. Хотите написать колонку для «Нетологии»? Читайте наши условия публикации. Чтобы быть в курсе всех новостей и читать новые статьи, присоединяйтесь к Телеграм-каналу Нетологии.
Линейная функция (ЕГЭ 2022)
Зависимость одной величины от другой математики называют функций одной величины от другой.
Количество денег — это функция вашей зарплаты (иногда говорят «от зарплаты»).
Вес — это функция от съеденных круассанов. Чем меньше съел, тем меньше весишь.
Расстояние — это функция времени. Чем дольше ты будешь идти, тем больше пройдешь.
Ну а теперь перейдем к одному из видов функций – линейной функции.
Линейная функция — коротко о главном
Линейная функция –это функция вида \( y=kx+b\), где \( k\) и \( b\) – любые числа (коэффициенты).
Рассмотрим, как коэффициенты влияют на месторасположение графика:
Общие варианты представлены на рисунке:
Линейная функция
Но сначала официальное определение «Функции» – теперь ты его поймешь. Держи в уме: деньги – зарплата, вес – круассаны, расстояние – время.
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция \( y=f\left( x \right)\), это значит что каждому допустимому значению переменной \( x\) (которую называют «аргументом») соответствует одно значение переменной \( y\) (называемой «функцией»).
Что значит «допустимому»?
Все дело в понятии «область определения»: для некоторых функций не все аргументы «одинаково полезны» — не все можно подставить в зависимость.
Например, для функции \( y=\sqrt
Ну и вернемся, наконец, к теме данной статьи.
Линейной называется функция вида \( y=kx+b\), где \( k\) и \( b\) – любые числа (они называются коэффициентами).
Другими словами, линейная функция – это такая зависимость, что функция прямо пропорциональна аргументу.
Как думаешь, почему она называется линейной?
Все просто: потому что графиком этой функции является прямая линия. Но об этом чуть позже.
Как уже говорилось в теме «Функции», важнейшими понятиями, связанными с любой функцией, являются ее область определения \( D\left( y \right)\) и область значений \( E\left( y \right)\).
Область определения линейной функции
Какими могут быть значения аргумента линейной функции \( y=kx+b\)? Правильно, любыми. Это значит, что область определения – все действительные числа:
\( D\left( y \right)=\mathbb
А множество значений?
Область значений линейной функции
Тут тоже все просто: поскольку функция прямо пропорциональна аргументу, то чем больше аргумент \( x\), тем больше значение функции \( y\).
Значит, \( y\) так же как и \( x\) может принимать все возможные значения, то есть \( E\left( y \right)=\mathbb
Верно, да не всегда. Есть такие линейные функции, которые не могут принимать любые значения. Как думаешь, в каком случае возникают ограничения?
Вспомним формулу: \( y=kx+b\). Какие нужно выбрать коэффициенты \( k\) и \( b\), чтобы значение функции y не зависело от аргумента \( x\)?
А вот какие: \( b\) – любое, но \( k=0\). И правда, каким бы ни был аргумент \( x\), при умножении на \( k=0\) получится \( 0\)!
Тогда функция станет равна \( y=0\cdot x+b=b\), то есть она принимает одно и то же значение при всех \( x\):
\( y = kx + b:<\rm< >>\left[ \begin
Теперь рассмотрим несколько задач на линейную функцию.
Три задачи на линейную функцию
Решение задачи №1
Пусть начальное значение аргумента равно некому числу \( <
Чему была равна функция до увеличения? Подставляем аргумент в формулу:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Решение задачи №2
Аналогично предыдущей задаче:
Начальное значение аргумента равно \( <
Начальное значение функции: \( <
В этот раз функция не увеличилась, а уменьшилась. Это значит, что конечное значение будет меньше начального, а значит, изменение (разность конечного и начального) будет отрицательным:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Определение прямой пропорциональной зависимости
Если проанализировать решения этих двух задач, можно прийти к важному выводу.
При изменении аргумента линейной функции на \( \Delta x\) функция изменяется на \( k\cdot \Delta x\). То есть изменение функции всегда ровно в \( \mathbf
\) раз больше изменения аргумента.
По сути это является определением прямой пропорциональной зависимости.
Решение задачи №3
Подставим известные значения аргумента и функции в формулу \( y=kx+b\):
Получили два уравнения относительно \( k\) и \( b\). Теперь достаточно решить систему этих двух уравнений:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
График линейной функции
Как я уже упоминал ранее, график такой функции – прямая линия.
Как известно из геометрии, прямую можно провести через две точки (то есть, если известны две точки, принадлежащие прямой, этого достаточно, чтобы ее начертить).
Предположим, у нас есть функция линейная функция \( y=2x+1\). Чтобы построить ее график, нужно вычислить координаты любых двух точек.
То есть нужно взять любые два значения аргумента \( x\) и вычислить соответствующие два значения функции.
Затем для каждой пары \( \left( x;y \right)\) найдем точку в системе координат, и проведем прямую через эти две точки.
Проще всего найти функцию, если аргумент \( x=0:y\left( 0 \right)=2\cdot 0+1=1\).
Итак, первая точка имеет координаты \( \left( 0;1 \right)\).
Теперь возьмем любое другое число в качестве \( x\), например, \( x=1:y\left( 1 \right)=2\cdot 1+1=3\).
Вторая точка имеет координаты \( \left( 1;3 \right)\).
Ставим эти две точки на координатной плоскости:
Теперь прикладываем линейку, и проводим прямую через эти две точки:
Вот и все, график построен!
Давай теперь на этом же рисунке построим еще два графика: \( y=
Построй их самостоятельно так же: посчитай значение y для любых двух значений \( x\), отметь эти точки на рисунке и проведи через них прямую.
Должно получиться так:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Видно, что все три прямые по-разному наклонены и в разных точках пересекают координатные оси. Все дело тут в коэффициентах \( \displaystyle k\) и \( \displaystyle b\).
Давай разберемся, на что они влияют.
Коэффициенты линейной функции
Для начала выясним, что делает коэффициент \( \displaystyle b\). Рассмотрим функцию \( \displaystyle y=x+b\), то есть \( \displaystyle k=1\).
Меняя \( \displaystyle b\) будем следить, что происходит с графиком.
Что ты можешь сказать о них? Чем отличаются графики?
Это сразу видно: чем больше \( \displaystyle b\), тем выше располагается прямая.
Более того, заметь такую вещь: график пересекает ось \( \displaystyle \mathbf
И правда. Как найти точку пересечения графика с осью \( \displaystyle y\)? Чему равен \( \displaystyle x\) в такой точке?
В любой точке оси ординат (это название оси \( \displaystyle y\), если ты забыл) \( \displaystyle x=0\).
Значит достаточно подставить \( \displaystyle x=0\) в функцию, и получим ординату пересечения графика с осью \( \displaystyle y\):
\( \displaystyle y=k\cdot 0+b=b\)
Теперь по поводу \( \displaystyle k\). Рассмотрим функцию \( \displaystyle \left( b=0 \right).\) Будем менять \( \displaystyle k\) и смотреть, что происходит с графиком.
Так, теперь ясно: \( \displaystyle k\) влияет на наклон графика.
Чем больше \( \displaystyle k\) по модулю (то есть несмотря на знак), тем «круче» (под большим углом к оси абсцисс – \( \displaystyle Ox\)) расположена прямая.
Если \( \displaystyle k>0\), график наклонен «вправо», при \( \displaystyle k
Выберем на графике две точки \( \displaystyle A\) и \( \displaystyle B\). Для простоты выберем точку \( \displaystyle A\) на пересечении графика с осью ординат. Точка \( \displaystyle B\) – в произвольном месте прямой, пусть ее координаты равны \( \displaystyle \left( x;y \right)\).
Рассмотрим прямоугольный треугольник \( \displaystyle ABC\), построенный на отрезке \( \displaystyle AB\) как на гипотенузе.
Из рисунка видно, что \( \displaystyle AC=x\), \( \displaystyle BC=y-b\).
Подставим \( \displaystyle y=kx+b\) в \( \displaystyle BC:BC=y-b=kx+b-b=kx\).
Получается, что \( BC = k \cdot AC<\rm< >> \Rightarrow <\rm< >>k = \frac<
Итак, коэффициент \( \displaystyle k\) равен тангенсу угла наклона графика, то есть угла между графиком и осью абсциссс.
Именно поэтому его (коэффициент \( \displaystyle k\)) обычно называют угловым коэффициентом.
В случае, когда \( k
Если же \( \displaystyle k=0\), тогда и \( <\mathop<\rm tg>\nolimits> \alpha = 0,\) следовательно \( \displaystyle \alpha =0\), то есть прямая параллельна оси абсцисс.
Понимать геометрическое значение коэффициентов очень важно, оно часто используется в различных задачах на линейную функцию.
Разбор еще трех задач на линейную функцию
1. Найдите коэффициенты \( \displaystyle k\) и \( \displaystyle b\) линейной функции, график которой приведен на рисунке. Запишите уравнение этой функции.
2. Найдите коэффициенты \( \displaystyle k\) и \( \displaystyle b\) линейной функции, график которой приведен на рисунке. Запишите уравнение этой функции.
3. График какой из функций изображен на рисунке?
Решение задачи №1
Коэффициент \( b\) найти проще простого – это ведь точка пересечения графика с осью \( \displaystyle Oy\):
Угловой коэффициент \( \displaystyle k\) – это тангенс угла наклона прямой.
Для его нахождения выберем две точки \( \displaystyle A\) и \( \displaystyle B\) на графике и построим прямоугольный треугольник с гипотенузой \( \displaystyle AB\):