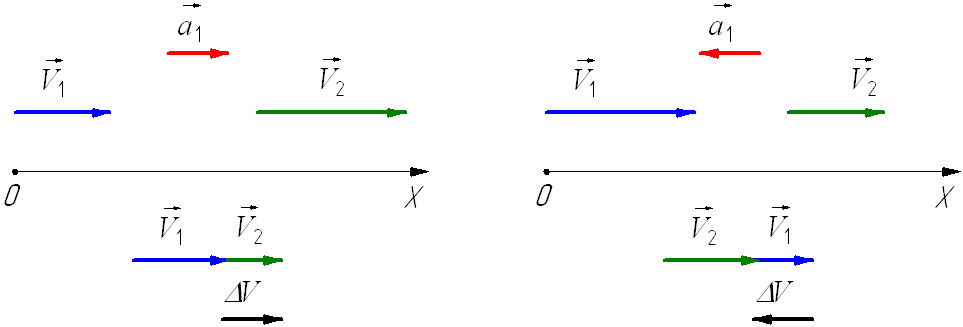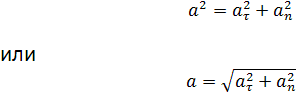что такое линейное ускорение
Что такое линейное ускорение
4.1. Движение по окружности с постоянной скоростью.
Движение по окружности — простейший вид криволинейного движения.
4.1.1. Криволинейное движение — движение, траекторий которого является кривая линия.
Для движения по окружности с постоянной скоростью:
1) траектория движения — окружность;
2) вектор скорости направлен по касательной к окружности;
3) вектор скорости постоянно меняет свое направление;
4) за изменение направления скорости отвечает ускорение, называемое центростремительным (или нормальным) ускорением;
5) центростремительное ускорение меняет только направление вектора скорости, при этом модуль скорости остается неизменным;
6) центростремительное ускорение направлено к центру окружности, по которой происходит движение (центростремительное ускорение всегда перпендикулярно вектору скорости).
4.1.2. Период (T) — время одного полного оборота по окружности.
Это величина постоянная, так как длина окружности постоянная и скорость движения постоянна
4.1.3 Частота — число полных оборотов за 1 с.
По сути, частота отвечает на вопрос: как быстро вращается тело?
4.1.4. Линейная скорость — показывает, какой путь проходит тело за 1 с (это та же самая скорость, о которой говорилось в предыдущих темах)
где R — радиус окружности.
4.1.5. Угловая скорость показывает, на какой угол поворачивается тело за 1 с.
где — угол, на который повернулось тело за время
4.1.6. Центростремительное ускорение
Напомним, что центростремительное ускорение отвечает только за поворот вектора скорости. При этом, так как скорость постоянная величина, то значение ускорения тоже постоянно.
4.1.7. Закон изменения угла поворота
Это полный аналог закона движения при постоянной скорости :
Роль координаты x играет угол роль начальной координаты
играет
скорость
— угловая скорость
И с формулой
следует работать так же, как ранее работали с формулой закона равномерного движения.
4.2. Движение по окружности с постоянным ускорением.
4.2.1. Тангенциальное ускорение
Центростремительное ускорение отвечает за изменение направления вектора скорости, но если еще меняется и модуль скорости, то необходимо ввести величину отвечающую за это — тангенциальное ускорение
Из вида формулы ясно, что
— это обычное ускорение, о котором говорилось раньше. Если
то справедливы формулы равноускоренного движения:
где S — путь, который проходит тело по окружности.
Итак, еще раз подчеркнем, отвечает за изменение модуля скорости.
4.2.2. Угловое ускорение
Мы ввели аналог скорости для движения по окружности — угловая скорость. Естественно будет ввести и аналог ускорения — угловое ускорение
Угловое ускорение связано с тангенциальным ускорением:
Из формулы видно, что если тангенциальное ускорение постоянно, то и угловое ускорение будет постоянно. Тогда можем записать:
Формула является полным аналогом закона равнопеременного движения, поэтому работать с этой формулой мы уже умеем.
4.2.3. Полное ускорение
Центростремительное (или нормальное) и тангенциальное ускорения не являются самостоятельными. На самом деле, это проекции полного ускорения на нормальную (направлена по радиусу окружности, то есть перпендикулярно скорости) и тангенциальную (направлена по касательной к окружности в сторону, куда направлен вектор скорости) оси. Поэтому
Нормальная и тангенциальные оси всегда перпендикулярны, следовательно, абсолютно всегда модуль полного ускорения можно найти по формуле:
4.4. Движение по криволинейной траектории.
Движение по окружности является частным видом криволинейного движения. В общем случае, когда траектория представляет собой произвольную кривую (см. рис.), всю траекторию можно разбить на участки: AB и DE — прямолинейные участки, для которых справедливы все формулы движения по прямой; а для каждой участка, который нельзя рассмотреть как прямую, строим касательную окружность (окружность, которая касается траектории только в этой точке) — в точках C и D. Радиус касательной окружности называется радиусом кривизны. В каждой точке траектории радиус кривизны имеет свое значение.
Формула для нахождения радиуса кривизны :
где — нормальное ускорение в данной точке (проекция полного ускорения на ось, перпендикулярную вектору скорости).
Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
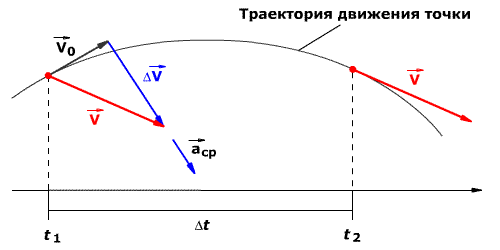
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
а направление вектора ускорения совпадает с вектором скорости
Если скорость тела по модулю уменьшается, то есть
то направление вектора ускорения противоположно направлению вектора скорости 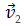
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения 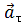
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 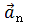
Полное ускорение
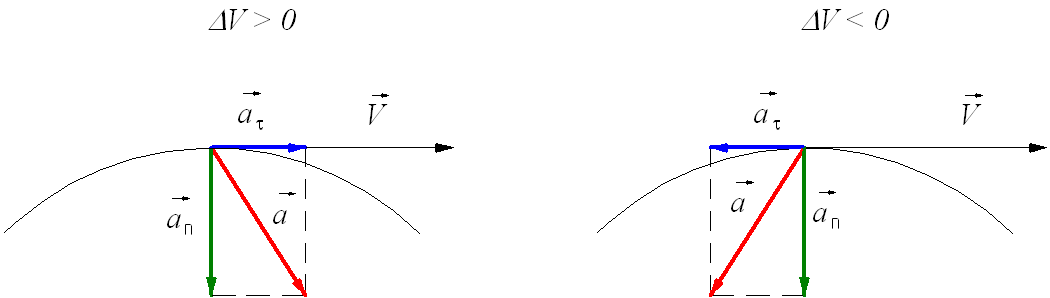
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
Какова формула линейного ускорения?
Формула линейного ускорения:
Впоследствии, почему именно V WR?
Тогда какова формула линейного движения?
Поскольку мы используем уравнение движения F = ma чтобы описать линейное движение, мы можем использовать его аналог τ = dLdt = r × F τ = d L dt = r × F, чтобы описать угловое движение.
Кроме того, что вызывает линейное ускорение?
Линейная сила (сила по прямой линии) f, приложенная к массе m, вызывает линейное ускорение a посредством соотношения, показанного в уравнениях 7.31 и 7.32. … Примерами таких сил являются сила тяжести, вязкость, трение, импульсные силы, возникающие при столкновениях, и силы, возникающие из-за подпружиненных элементов.
Как вы рассчитываете линейное движение?
Угловая скорость ω аналогична линейной скорости v. Связь между линейной скоростью и угловой скоростью можно записать двумя разными способами: v = rω или ω = v / r.
Что такое линейная скорость?
Линейная скорость расстояние, пройденное движущимся объектом. Скорость, с которой объект движется по линейной траектории, называется линейной скоростью.
Какие бывают 4 типа движений?
Какие 5 переменных в линейном движении?
Что такое пример линейного движения?
Линейное движение можно определить как движение тела по прямой без каких-либо отклонений. Важными примерами линейного движения являются: Спортсмен бежит по прямой дорожке в парке, пуля из пистолета всегда движется по прямой и т. д.
Что вы имеете в виду под линейным ускорением?
Линейное ускорение. Скорость изменения скорости без изменения направления; например, когда скорость самолета увеличивается при движении по прямой.
В контексте кругового движения линейное ускорение также называется тангенциальное ускорение at. Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления.
Какая связь между линейной и угловой скоростью?
Мы можем записать взаимосвязь между линейной скоростью и угловой скоростью двумя разными способами: v = rω или ω = v / r.
Какие 5 уравнений движения?
В условиях постоянного ускорения эти более простые уравнения движения обычно называют уравнениями «СУВАТ», возникающими из определений кинематических величин: смещение (S), начальная скорость (u), конечная скорость (v), ускорение (a) и время (t).
Что такое R * Omega?
Какова размерная формула Омеги?
Таким образом, с радиусом орбиты 42,000 км от центра Земли скорость спутника в космосе составляет v = 42,000 км × 0.26 / ч ≈ 11,000 км / ч.
| Угловая скорость | |
|---|---|
| Производные от других величин | ω = dθ / dt |
| Размеры |
Какова формула Омеги?
Угловая частота ω (в радианах в секунду) больше частоты ν (в циклах в секунду, также называемая Гц) в 2π раз. … Точки, находящиеся дальше от оси, перемещаются быстрее, удовлетворительно ω = v / r.
Угловая скорость выше линейной?
Линейная скорость всегда больше угловой скорости. Линейная скорость может быть измерена в милях в час. Линейная скорость может быть измерена в градусах. Угловая скорость зависит от длины.
Какой пример линейной скорости?
Пояснение: Линейная скорость определяется как расстояние за период времени. Например, если человек пробежал 1 милю или приблизительно 1600 метров за 7 минут, он бы преодолел около 230 метров в минуту.
Какие есть 5 типов движения?
Есть разные типы движения: поступательное, вращательное, периодическое и непериодическое движение.
В чем разница между линейным и поступательным движением?
Какой тип движения самый распространенный?
Общее движение это наиболее распространенный вид движения в спорте и физических упражнениях.
Какие два типа линейного движения?
Два типа линейного движения: равномерное движение и неравномерное движение и три типа прямолинейного движения: равномерное прямолинейное движение, равноускоренное прямолинейное движение и прямолинейное движение с неравномерным ускорением.
В чем разница между линейным и прямолинейным движением?
Ответ: Говорят, что тело / объект движется линейно. когда он движется по прямой или по кривой на плоскости. Пример: спортсмен бежит по прямой дорожке. … Другими словами, когда тело движется только по прямому пути, говорят, что оно движется по прямой.
Линейные скорости и ускорения точек вращающегося тела



Линейные скорости и ускорения точек вращающегося тела
вращающегося тела называют линейными. Для их определения достаточно одной точки М(рис. 11.5). Как уже указывалось, траектория его движения представляет собой дугу окружности. В первый момент точка м находится в положении Л40, и время с позиции Афи. Возьмем начало координат в точке Mo,
так что положительное направление координаты кривизны s совпадает с Людмила Фирмаль
направлением увеличения угла поворота тела. Тогда координаты s будут равны длине дуги M0L1|, но из геометрии видно, что длина дуги окружности равна радиусу, умноженному на соответствующий центральный угол. s=/?Р. (1 1 1. 1 4 ) Мы различаем результирующее равенство во времени: ds__ _ _ d(/? 2=/? ] / Е2+П2. (11.18) Из Формулы (11.18) следует, что чем дальше точка удаляется от оси вращения, тем больше ускорение.
Например. Шестерня / Шестерня 2 (Рис. 11.7) из оставшегося состояния начинает вращаться равномерно ускоренно с угловым ускорением 81=0,1 Радиана / сек. Решение. Так как начальная угловая скорость первой передачи равна нулю(Oi=ei/+0, l-T. Закон равного вращения первой шестерни равен= Людмила Фирмаль
Если вам потребуется заказать решение по технической механике вы всегда можете написать мне в whatsapp.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Как найти ускорение — определение и формулы расчета в физике
Что такое ускорение
Ускорение \(\overrightarrow а\) — векторная величина в физике, характеризующая быстроту изменения скорости тела.
Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.
Единица измерения
В СИ (системе интернациональной) ускорение измеряется: \( \begin
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как рассчитать ускорение: формулы
Для прямолинейного движения
Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.
В этом случае ускорение находится по следующим формулам:
Где \(a\) — достигнутое ускорение тела, \(S\) — пройденный путь (расстояние), \(t\) — затраченное время.
Время отсчитывается от начала движения тела.
При прямолинейном равномерном движении ускорение по модулю равняется нулю.
Для равноускоренного движения
Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).
Для равнозамедленного движения
Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).
Нахождение ускорения через массу и силу
Принцип инерции Галилея:
Если не действовать на тело, то его скорость не будет меняться.
Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.
Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.
Выражается по формуле:
Максимальное ускорение
\(a_
Среднее ускорение
Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.
Проекция ускорения
Определение проекции ускорения на ось \(х\) :