что такое линейное множество

Линейные множества

ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ

Основные понятия

Под множествомобычно понимают некоторый набор (совокупность) элементов произвольной природы. Например, совокупность короткозамкнутых асинхронных двигателей серии 4A, набор сопротивлений и т.д. Множества вещественных, натуральных и целых чисел являются примером числовых множеств.

Каждый из таких элементов в отдельности есть элемент множества. Фразу «е является элементом множества Е» («е принадлежит множеству Е») записывают, кратко в виде еÎЕ. Если е не принадлежит множеству Е, то пишут е ÏЕ.

Пусть a, b, c… – элементы множества E. Используя фигурные или круглые скобки можно записать

Если элементы множества E суть все целые числа от k до l (k

Операция пересечения множеств обладает сведущими свойствами:

Объединение множеств E₁ и E₂ (E₁ÈE₂) есть множество всех элементов e, содержащихся либо в E₁, либо в E₂, либо и в E₁ и в E₂ (рис. 2.3, б), т.е. в объединении находятся элементы, принадлежащие E₁, E₂ и обоим множествам вместе. Операция объединения множеств обладает следующими свойствами:

Разностьюмножеств E₁ и E₂ называют множество, состоящее из элементов, которые принадлежат множеству E₁, но не принадлежат множеству E₂ (E₁\E₂) т.е. совокупность всех eÎE₁, таких что e E₂ (рис. 2.3, в).

Рис. 2.3. Пересечение (а), объединение (б), разность (в) множеств

Если E₂ – одноэлементное множество, т.е. E₂ = <e>, то E₁\<e> будем записывать и проще: E₁–e. Число элементов во множестве E₁ (обозначается |E₁| = e) называется мощностьюконечного множества. Для бесконечного множества E₂ мощность считается равной бесконечности (|E₂| = ∞).

1) Если вектора xи y принадлежат M, тоx+y также принадлежит M.

2)Если произвольный вектор x принадлежит M, то lx при любом вещественном значении числа l также принадлежит M.

Рис. 2.4. Подпространство и линейное многообразие

Если максимальное число линейно независимых векторов, которые можно найти в M, равно r, то говорят, что M – r-мерное подпространство. Само пространство E n можно рассмотреть как n– мерное пространство.

Гиперплоскостьюв E n называется множество точек x, удовлетворяющих уравнению

Обычно приставку гиперупотребляют для обозначения пространств, имеющих более чем три измерения. Гиперплоскость = 0 содержит начало координат и является объединением всех прямых, которые проходят через начало координат и направляющие векторы которых ортогональны а,т.е. гиперплоскость есть множество точек, принадлежащим этим прямым

Гиперплоскость задает два замкнутых полупространства (рис. 2.5)

а также два открытых пространства

Н + _ab = <xÎE n | > b>, Н + _ab = <xÎE n | + _ab (рис. 2.5). Гиперплоскость Н_ab и соответствующие полупространства могут быть записаны с помощью некоторой фиксированной точки ÎН_ab. При любом вещественном числе b уравнение = b определяет линейное многообразие. Если задан некоторый вектор x 0 ÎE n такой, что 0 > = b, то линейное многообразие, определяемое уравнением = b, можно рассматривать как смещение Н_ab на x₀

Любую гиперплоскость в E n можно задать в виде множества решений уравнения (2.1), подобрав соответствующим образом вектор a и число b.

Любую прямую в E n можно задать в виде

<xÎE n | x= a+lc, lÎE> (2.2)

Отрезком,соединяющим две данные точки x₁, x₂ в E n называется множество таких точек, координаты x_j которых связаны с координатами x₁ и x₂ соотношениями вида

Конкретный выбор l определяет положениеx на отрезке (при l = 1 точка xсовпадает с x₁, при l = 0 – с x₂, при 0

Дата добавления: 2015-04-12 ; просмотров: 11 | Нарушение авторских прав

Источник

Линейно упорядоченное множество

Линейно упорядоченное множество или цепь ― частично упорядоченное множество, в котором для любых двух элементов и имеет место или .

Важнейший частный случай линейно упорядоченных множеств ― вполне упорядоченные множества.

Связанные определения

Сечением линейно упорядоченного множества называется разбиение его на два подмножества и так, что , и для любых и , Классы и называются соответственно нижним и верхним классами сечения.

Различаются следующие типы сечений:

Линейно упорядоченное множество называется непрерывным, если все его сечения дедекиндовы.

Подмножество линейно упорядоченного множества называется плотным, если каждый неодноэлементный интервал множества содержит элементы, принадлежащие .

Источник

Линейные множества

Непустое подмножество M(Ē) пространства E n называется (вещественным) линейным подпространством(рис. 2.4), если оно удовлетворяет следующим двум условиям:

1) Если вектора xи y принадлежат M, тоx+y также принадлежит M.

2)Если произвольный вектор x принадлежит M, то lx при любом вещественном значении числа l также принадлежит M.

Рис. 2.4. Подпространство и линейное многообразие

Если максимальное число линейно независимых векторов, которые можно найти в M, равно r, то говорят, что M – r-мерное подпространство. Само пространство E n можно рассмотреть как n– мерное пространство.

Гиперплоскостьюв E n называется множество точек x, удовлетворяющих уравнению

Обычно приставку гиперупотребляют для обозначения пространств, имеющих более чем три измерения. Гиперплоскость = 0 содержит начало координат и является объединением всех прямых, которые проходят через начало координат и направляющие векторы которых ортогональны а,т.е. гиперплоскость есть множество точек, принадлежащим этим прямым

Гиперплоскость задает два замкнутых полупространства (рис. 2.5)

а также два открытых пространства

Н + _ab = <xÎE n | > b>, Н + _ab = <xÎE n | + _ab (рис. 2.5). Гиперплоскость Н_ab и соответствующие полупространства могут быть записаны с помощью некоторой фиксированной точки 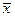ÎН_ab. При любом вещественном числе b уравнение = b определяет линейное многообразие. Если задан некоторый вектор x 0 ÎE n такой, что 0 > = b, то линейное многообразие, определяемое уравнением = b, можно рассматривать как смещение Н_ab на x₀

Любую гиперплоскость в E n можно задать в виде множества решений уравнения (2.1), подобрав соответствующим образом вектор a и число b.

Любую прямую в E n можно задать в виде

<xÎE n | x= a+lc, lÎE> (2.2)

Отрезком,соединяющим две данные точки x₁, x₂ в E n называется множество таких точек, координаты x_j которых связаны с координатами x₁ и x₂ соотношениями вида

Конкретный выбор l определяет положениеx на отрезке (при l = 1 точка xсовпадает с x₁, при l = 0 – с x₂, при 0

Источник

Большая Энциклопедия Нефти и Газа

Линейное множество

Линейные множества часто называют векторными пространствами. [4]

Линейное множество Л называется алгеброй, если на нем определена операция умножения, линейная относительно каждого сомножителя в отдельности. [5]

Конечномерное линейное множество Х0 в нормированном пространстве X замкнуто. [6]

Иногда линейное множество функций со скалярным произведением, удовлетворяющим указанным свойствам, называют функциональным гильбертовым пространством. Векторы состояний квантовых систем образуют функциональное гильбертово пространство. [7]

Рассмотрим линейное множество R всех действительных функций, заданных на всей действительной прямой. [11]

Замыкание линейного множества Х0 в пространстве X есть линейное множество. [12]

Два линейных множества X и У называются изоморфными, если между элементами этих множеств можно установить взаимно однозначное соответствие, сохраняющее операции сложения и умножения на число. При изоморфизме линейных множеств ноль переходит в ноль. Изоморфные линейные множества могут отличаться природой самих элементов. Однако все соотношения, полученные между элементами одного линейного множества посредством операций сложения и умножения на число, будут справедливы и для любого другого линейного множества, изоморфного первому. [13]

В бесконечномерном линейном множестве Е существуют счетные линейно независимые системы элементов. В самом деле, любой элемент хг Э образует линейно независимую систему, состоящую из одного элемента. [14]

Источник

ЛИНЕЙНО УПОРЯДОЧЕННОЕ МНОЖЕСТВО,

Полезное

Смотреть что такое «ЛИНЕЙНО УПОРЯДОЧЕННОЕ МНОЖЕСТВО,» в других словарях:

Упорядоченное множество — Упорядоченное множество множество с заданным отношением порядка. Частично упорядоченное множество Линейно упорядоченное множество Вполне упорядоченное множество … Википедия

УПОРЯДОЧЕННОЕ МНОЖЕСТВО — множество, на к ром задано отношение порядка. См. также Линейно упорядоченное множество, Частично упорядоченное множество … Математическая энциклопедия

Частично упорядоченное множество — У этого термина существуют и другие значения, см. Упорядоченное множество. Подмножества , упо … Википедия

Вполне упорядоченное множество — У этого термина существуют и другие значения, см. Упорядоченное множество. Вполне упорядоченное множество линейно упорядоченное множество M такое, что в любом его непустом подмножестве есть минимальный элемент, другими словами это… … Википедия

УПОРЯДОЧЕННОЕ КОЛЬЦО — частично упорядоченное кольцо, кольцо R(не обязательно ассоциативное), являющееся частично упорядоченной группой по сложению, в к ром для любых a, b, неравенства и влекут за собой неравенства и Всякое кольцо является У. к. с тривиальным порядком … Математическая энциклопедия

НЕПРЕРЫВНОЕ МНОЖЕСТВО — (линейно) упорядоченное множество X, все собственные сечония к рого являются дедекиндовыми сечениями, т. е. при любом разбиении Xна два непустых подмножества X и X» таком, что каждый элемент из X предшествует каждому элементу из X»,… … Математическая энциклопедия

ПОРЯДКОВЫЙ ТИП — линейно упорядоченного множества А свойство множества А, к рое присуще любому линейно упорядоченному множеству В, подобному А. При этом два множества Аи В, линейно упорядоченные соотношениями R и S, наз. подобными, если существует функция f,… … Математическая энциклопедия

Источник