что такое линейная засечка
Основы геодезии
О геодезии и разный полезный материал для геодезистов.
Линейная засечка
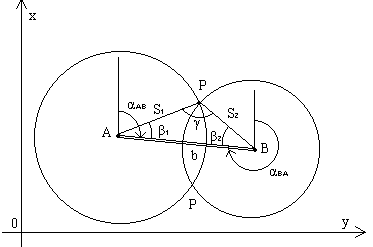
Графическое решение. Проведем вокруг пункта A окружность радиусом S1 (в масштабе чертежа), а вокруг пункта B – окружность радиусом S2; точка пересечения окружностей является искомой точкой; задача имеет два решения, так как две окружности пересекаются в двух точках (рис.2.9).
Исходные данные: XA, YA, XB, YB,
Измеряемые элементы: S1, S2,
Неизвестные элементы: X, Y.
Аналитическое решение. Рассмотрим два алгоритма аналитического решения, один – для ручного счета (по способу треугольника) и один – для машинного счета.
Алгоритм ручного счета состоит из следующих действий:
1. решение обратной геодезической задачи между пунктами A и B и получение дирекционного угла αAB и длины b линии AB,
2. вычисление в треугольнике ABP углов β1 и β2 по теореме косинусов: 
3. вычисление угла засечки γ 
4. вычисление дирекционных углов сторон AP и BP:
пункт P справа от линии AB 
пункт P слева от линии АВ 
5. решение прямых геодезических задач из пункта A на пункт P и из пункта B на пункт P:
Результаты обоих решений должны совпадать.
Алгоритм машинного решения линейной засечки состоит из следующих действий:
1. решение обратной геодезической задачи между пунктами A и B и получение дирекционного угла αAB и длины b линии AB,
2. введение местной системы координат X’O’Y’ с началом в точке A и осью O’X’, направленной вдоль линии AB, и пересчет координат пунктов A и B из системы XOY в систему X’O’Y’: 
3. запись уравнений окружностей в системе X’O’Y’: 
и совместное решение этих уравнений, которое предусматривает раскрытие скобок во втором уравнении и вычитание второго уравнения из первого: 
Если искомая точка находится слева от линии AB, то в формуле (2.39) берется знак “-“, если справа, то “+”.
4. пересчет координат X’ и Y’ точки P из системы X’O’Y’ в систему XOY по формулам (2.2): 
Линейная засечка.
Задача линейной засечки заключается в определении координат третьего пункта по координатам исходных пунктов и измеренным расстояниям от определяемого пункта до исходных (однократная засечка). Для контроля определения используются координаты третьего исходного пункта и расстояния до него от определяемого.
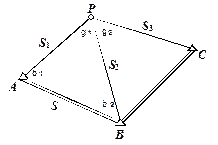 Рис. 2.24. Рис. 2.24. | Даны координаты пунктов А, B, C. Измерены линии S1, S2, S3. Требуется определить координаты точки P (X, Y). Рассмотрим однократную засечку с использованием пунктов А и В (рис. 2.24). 1. Решением обратной геодезической задачи определим дирекционный угол и длину линии АВ: |
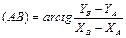
2. Определим угол β1, используя теорему косинусов:
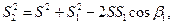
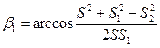
3. Определим дирекционный угол линии АР
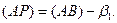
4. Определим координаты точки Р:
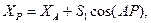
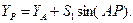
Для контроля решения задачи вычисляется длина линии ВР и сравнивается с измеренной
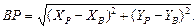
Расхождение не должно превышать 3 единиц последнего знака в измеренном значении линии S2.
Для полного контроля определения вычисляется сторона СР и сравнивается с измеренной S3
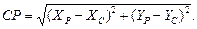
Тема: Геодезические сети. Топографические съемки
_______ Для составления карт и планов, решения геодезических задач в том числе геодезического обеспечения строительства, на поверхности Земли располагают ряд точек, связанных между собой единой системой координат. Эти точки маркируют на поверхности Земли или в зданиях и сооружениях центрами (знаками).
_______ Геодезическая сеть – это система закрепленных точек земной поверхности, положение которых определено в общей для них системе геодезических координат.
_______ Геодезические сети подразделяют на плановые и высотные : первые служат для определения координат X и Y геодезических центров, вторые — для определения их высот.
_______ Принцип построения плановых геодезических сетей заключается в следующем. На местности выбирают точки, взаимное положение которых представляется в виде геометрических фигур: треугольников, четырехугольников, ломаных линий и т.д. Причем точки выбирают с таким расчетом, чтобы некоторые элементы фигур (стороны, углы) можно было бы непосредственно измерить, а все другие элементы вычислить по данным измерений. Например, в треугольнике достаточно измерить одну сторону и три угла (один для контроля правильности измерений) или две стороны и два угла (один для контроля правильности измерений), а остальные стороны и углы вычислить. Для вычисления плановых координат вершин выбранных точек необходимо кроме элементов геометрических фигур знать еще дирекционный угол стороны одной из фигур и координаты одной из вершин.
_______ Сети строят по принципу перехода от общего к частному, т. е. от сетей с большими расстояниями между пунктами и высокоточными измерениями к сетям с меньшими расстояниями и менее точным.
_______ Геодезические сети подразделяют на четыре вида: государственные, сгущения, съемочные и специальные. Государственные геодезические сети служат исходными для построения всех других видов сетей. Началом единого отсчета плановых координат в Российской Федерации служит центр круглого зала Пулковской обсерватории в Санкт-Петербурге.
2. Методы создания геодезических сетей
_______ Плановые геодезические сети создаются методами триангуляции, полигонометрии и трилатерации. При построении геодезической сети методом триангуляции на местности закрепляется ряд точек, которые в своей совокупности образуют систему треугольников. В треугольниках измеряются все углы и некоторые стороны, которые называются базисными. По длине базисной стороны и измеренным углам, вычисляют длины всех сторон, а затем координаты всех пунктов сети.
 |
_______ Метод полигонометрии заключается в построении на местности системы ломанных линий, называемых полигонометрическими ходами. Эти ходы прокладывают обычно между пунктами триангуляции. В полигонометрических ходах измеряются все углы поворота и длины всех сторон.
 |
_______ При построении сети методом трилатерации на местности также строится сеть треугольников, в которых при помощи высокоточных дальномеров измеряются все стороны.
 |
_______ Сети сгущения строят для дальнейшего увеличения плотности (числа пунктов, приходящихся на единицу площади) государственных сетей. Плановые сети сгущения подразделяют на 1-й.и 2-й разряды.
_______ Съемочные сети — это тоже сети сгущения, но с еще большей плотностью. С точек съемочных сетей производят непосредственно съемку предметов местности и рельефа для составления карт и планов различных масштабов.
_______ Специальные геодезические сети создают для геодезического обеспечения строительства сооружений. Плотность пунктов, схема построения и точность этих сетей зависят от специфических особенностей строительства.
_______ Государственные высотные геодезические сети создают для распространения по всей территории страны единой системы высот. За начало высот в Российской Федерации и некоторых других странах принят средний уровень Балтийского моря, определение которого проводилось в период с 1825 до 1840 г. Этот уровень отмечен горизонтальной чертой на медной металлической пластине, укрепленной в устое моста через обводной канал в Кронштадте.
_______ Между пунктами государственных высотных геодезических сетей высокой точности (1-го класса) размещают пункты высотных сетей низших классов (2-го, 3-го и т.д.). Несколько пересекающихся ходов называют сетями. Как правило, сети создают из ходов, прокладываемых между тремя или более точек. В целом точки (реперы) высотных сетей, называемых нивелирными, достаточно равномерно распределены на территории страны.
_______ На незастроенной территории расстояния между реперами составляют 5. 7 км, в го- родах сеть реперов в 10 раз плотнее
_______ Для решения ограниченного круга вопросов при изысканиях, строительстве и эксплуатации зданий и сооружений создают высотную сеть технического класса.
_______ Как правило, сети образуют полигоны с узловыми точками (общими точками пересечения двух или более ходов одного и того же класса). Каждый нивелирный ход опирается обоими концами на реперы ходов более высокого класса или узловые точки.
3. Закрепление на местности пунктов геодезических сетей
_______ Точки геодезических сетей закрепляют на местности знаками. По местоположению знаки бывают: грунтовые и стенные, заложенные в стены зданий и сооружений; металлические, железобетонные, деревянные, в виде откраски и т.д.; по назначению — постоянные, к которым относятся все знаки государственных геодезических сетей, и временные, устанавливаемые на период изысканий, строительства, реконструкции, наблюдений и т.д.
 |
_______ Для того чтобы с одного знака был виден другой (смежный),над подземными центрами устанавливают наружные знаки в виде металлических или деревянных трех- или четырехгранных пирамид или сигналов.
 |
_______ Как правило, пункты плановых разбивочных сетей и сетей сгущения закрепляют подземными центрами, такими же как и пункты государственных сетей. Так как расстояния между этими пунктами сравнительно небольшие, оформления их наружными знаками не требуется. Знаки могут закладывать в зданиях и сооружениях, в этом случае их называют стенными.
_______ Иногда для различных целей могут создаваться местные геодезические сети. Обязательным требованием при установлении местных систем координат является обеспечение возможности перехода от местной системы координат к государственной системе координат, который осуществляется с использованием параметров перехода (ключей).
_______ Каждая местная система координат может создаваться с одной или несколькими трех или шести градусными зонами. Параметры местных систем координат и ключи перехода к государственной системе координат (формулы и правила, по которым координаты точек в одной системе можно получить в другой системы) устанавливает Росреестр по согласованию с Минобороны РФ.
4. Топографические съемки, ее виды
_______ Существуют следующие виды топографических съемок:
_______ • теодолитная (горизонтальная),
_______ • мензульная и др.
4.1 Что такое теодолитная съемка
_______ Теодолитной съемкой называется горизонтальная или контурная съемка местности, которая выполняется с помощью теодолита.
_______ Для проектирования зданий, сооружений необходимо на район строительства иметь топографические материалы – планы, карты. При отсутствии таких материалов выполняют съемку данного участка местности.
4.2 Сущность теодолитной съемки
_______ Теодолитная съемка выполняется с помощью теодолита и рулетки (или дальномера соотвествующей точности). В результате теодолитной съемки получают контурный план местности.
_______ Съемку контуров выполняют на основе съемочных теодолитных ходов, которые прокладываются в виде :
а) замкнутых ходов,
б) разомкнутых ходов,
в) диагональных ходов.
 |
 |
_______ Теодолитная съемка складывается из следующих видов работ :
• прокладка теодолитных ходов и привязка их к пунктам геодезической сети,
• съемка ситуации,
• обработка результатов полевых измерений,
• построение плана.
5. Прокладка теодолитных ходов. Привязка к пунктам геодезической сети
_______ Привязка теодолитных ходов заключается в измерении привычных углов между сторонами теодолитного хода и геодезической сети, обязательно с контролем.
 |
6. Съемка ситуации
_______ Съемка ситуации заключается в привязке контуров и предметов местности к сторонам и вершинам теодолитного хода.
6.1. Способ прямоугольных координат (способ перпендикуляров)
 |
6.2. Способ полярных координат (полярный способ)
 |
6.3. Способ линейных засечек
_______ Треугольники стараются делать близкими к равносторонним. Линейная засечка применяется часто при съемке строений. В этом случае расстояния измеряются лентой или рулеткой.
 |
6.4. Способ угловых засечек
_______ Способ угловых засечек применяется в тех случаях, когда определить положение точки при помощи линейных измерений не удается.
 |
6.5. Способ створов
 |
_______ Абрис – это схематический чертеж, составленный в произвольном масштабе.
_______ На абрисе зарисовывается снимаемая ситуация и записываются результаты выполняемых при съемке угловых и линейных измерений. Абрис составляется отдельно на каждую сторону теодолитного хода. На основе абриса производится нанесение контуров местности на план.
2.1.7. Линейная засечка
Исходные данные: XA, YA, XB, YB,
Измеряемые элементы: S1, S2,
Неизвестные элементы: X, Y.
Алгоритм ручного счета состоит из следующих действий:
решение обратной геодезической задачи между пунктами A и B и получение дирекционного угла αAB и длины b линии AB,
вычисление в треугольнике ABP углов β1 и β2 по теореме косинусов:
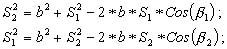
вычисление угла засечки γ

вычисление дирекционных углов сторон AP и BP:
пункт P справа от линии AB

пункт P слева от линии АВ

решение прямых геодезических задач из пункта A на пункт P и из пункта B на пункт P:

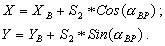
Результаты обоих решений должны совпадать.
Алгоритм машинного решения линейной засечки состоит из следующих действий:
решение обратной геодезической задачи между пунктами A и B и получение дирекционного угла αAB и длины b линии AB,
введение местной системы координат X’O’Y’ с началом в точке A и осью O’X’, направленной вдоль линии AB, и пересчет координат пунктов A и B из системы XOY в систему X’O’Y’:

запись уравнений окружностей в системе X’O’Y’:

и совместное решение этих уравнений, которое предусматривает раскрытие скобок во втором уравнении и вычитание второго уравнения из первого:

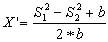

Если искомая точка находится слева от линии AB, то в формуле (2.39) берется знак «-«, если справа, то «+».
пересчет координат X’ и Y’ точки P из системы X’O’Y’ в систему XOY по формулам (2.2):
2.1.8. Обратная угловая засечка
К элементарным измерениям относится и измерение угла β на определяемой точке P между направлениями на два пункта A и B с известными координатами XA, YA и XB, YB (рис.2.10). Однако, это измерение оказывается теоретически довольно сложным, поэтому рассмотрим его отдельно.
Проведем окружность через три точки A, B и P. Из школьного курса геометрии известно, что угол с вершиной на окружности измеряется половиной дуги, на которую он опирается. Центральный угол, опирающийся на ту же дугу, измеряется всей дугой, следовательно, он будет равен 2β (рис.2.10).
Расстояние b между пунктами A и B считается известным, и из прямоугольного треугольника FCB можно найти радиус R окружности:

Уравнение окружности имеет вид:
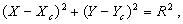
Обратной угловой засечкой называют способ определения координат точки P по двум углам β1 и β2, измеренным на определяемой точке P между направлениями на три пункта с известными координатами A, B, C (рис.2.11).
Графическое решение. Приведем способ Болотова графического решения обратной угловой засечки. На листе прозрачной бумаги (кальки) нужно построить углы β1 и β2 с общей вершиной P; затем наложить кальку на чертеж и, перемещая ее, добиться, чтобы направления углов на кальке проходили через пункты A, B, C на чертеже; переколоть точку P с кальки на чертеж.
Исходные данные: XA, YA, XB, YB, XC, YC;
Измеряемые элементы: β1, β2.
Неизвестные элементы: X, Y.
Предположим, что положение точки P известно, и проведем две окружности: одну радиусом R1 через точки A, B и P и другую радиусом R2 через точки B, C и P (рис.2.11). Радиусы этих окружностей получим по формуле (2.41):
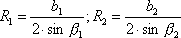
Координаты центра O1 можно найти по формулам линейной засечки из точек A и B по расстояниям R1, причем из двух решений нужно взять то, которое соответствует величине угла β1: если β1 90o, то точка O1 находится слева от линии AB.
Координаты центра O2 находятся по формулам линейной засечки из точек B и C по расстояниям R2, и одно решение из двух возможных выбирается по тому же правилу: если β2 90o, то точка O2 находится слева от линии BC.
Задача не имеет решения, если все четыре точки A, B, C и P находятся на одной окружности, так как обе окружности сливаются в одну, и точек их пересечения не существует.
Расчет разбивочных элементов в геодезии
Практически каждое строительство начинается с составления чертежа будущего объекта и проведения разбивочных работ, задачей которых является перенос на местность основных элементов проектной документации.
После установки местоположения точек, выставляются соответствующие метки, указывающие точное место возведения зданий и сооружений. Для обеспечения максимальной точности переноса точек, специалисты строят проектные углы и откладывают расстояния, переносят отметки и уклоны.
Способов проведения разбивочных работ есть немало, выбор зависит от условий местности, типа и габаритов конструкций, точности перенесения точек.
Способы разбивочных работ
Боковое нивелирование
Применяется для выноса осей в процессе проведения детальной разбивки и при установке конструкций в проектное положение.
Пересечение проектной точки К с конструкцией рассчитывается следующим образом. От точек А и В откладываются равные отрезки l для получения точек А’, В’ и линии А’В’. Над точкой А’ выставляется теодолит и наводится на точку В’. К горизонтальной конструкции прикладывается рейка и перемещается так, чтобы отсчет по ней был равен l. Пятка рейки даст положение точки К. Также определяется и положение точки К’.
Способ полярных координат
Используется при разбивке сооружений с пунктов теодолитных и полигонометрических ходов, если расстояние между исходными и выносимыми точками небольшое.
Горизонтальное положение d выясняется по формуле
Проконтролировать правильность положения точки К можно, отложив угол β’ от линии ВА и провести линию d’.
Прямая угловая засечка
Здесь положение К определяется при помощи отложения опорной линии АВ и углов β1 и β2, как на чертеже. Базой для b есть сторона разбивочной сетки либо его значение. Проектные углы β1 и β2 вычисляются путем определения разности дирекционных углов.
Способ линейной засечки
Задействуется для разбивки осей строительных конструкций. При помощи рулетки от точки А откладывается d1, от точки В – d2, место пересечения линий обозначается точкой К, которая и является проектной.
Метод пересечения створов
Используется для выноса в натуру труднодоступных точек проекта, если применение других технологий невозможно. На местности створы Т1Т’1 и Т2Т’2 задаются точками их пересечения с опорными сторонами. Местоположение точек Т1 и Т2 определяется горизонтальными продолжениями d1 и d2 от точки В вдоль опорных линий ВА и ВС, а точек Т’1 и Т’2 – от точки Е вдоль линий EF и ED.
Способ прямоугольных координат
Разбивочные работы довольно сложные и заказывать их лучше у профессионалов.