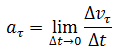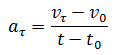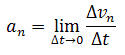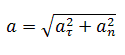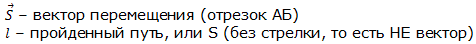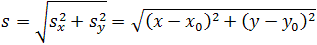что такое криволинейное движение

Криволинейное движение

Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению.

Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).

Рис. 1.19. Траектория и вектор перемещения при криволинейном движении.

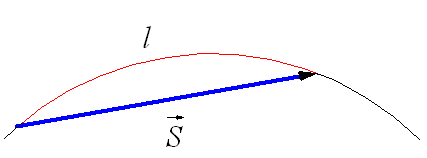
При движении по криволинейной траектории вектор перемещения направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).

Рис. 1.20. Мгновенная скорость при криволинейном движении.

Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение:

Где v_τ, v₀ – величины скоростей в момент времени t₀ + Δt и t₀ соответственно.

Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.

Нормальное ускорение — это изменение скорости по направлению за единицу времени:

Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.

Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности.

Полное ускорение при равнопеременном криволинейном движении тела равно:

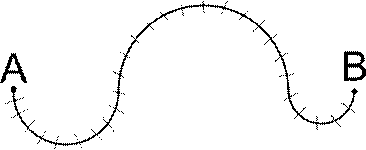
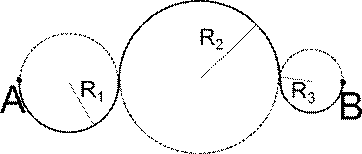
Движение тела по криволинейной траектории можно приближённо представить как движение по дугам некоторых окружностей (рис. 1.21).

Рис. 1.21. Движение тела при криволинейном движении.

Источник

Результаты поиска: Криволинейное движение

Криволинейное движение

Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению.

Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).

Рис. 1.19. Траектория и вектор перемещения при криволинейном движении.

При движении по криволинейной траектории вектор перемещения направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).

Рис. 1.20. Мгновенная скорость при криволинейном движении.

Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение:

Где v_τ, v₀ – величины скоростей в момент времени t₀ + Δt и t₀ соответственно.

Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.

Нормальное ускорение — это изменение скорости по направлению за единицу времени:

Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.

Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности.

Полное ускорение при равнопеременном криволинейном движении тела равно:

Движение тела по криволинейной траектории можно приближённо представить как движение по дугам некоторых окружностей (рис. 1.21).

Рис. 1.21. Движение тела при криволинейном движении.

Траектория

Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.

Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.

Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.

Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.

Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.

Вектор перемещения

Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.

Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.

Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).

Рис. 1.1. Вектор перемещения и пройденный путь.

Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.

Правило сложения векторов

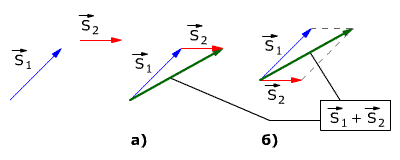
Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).

Рис. 1.2. Сложение векторов перемещений.

На рис 1.2 показаны правила сложения векторов S1 и S2:

а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма

Проекции вектора перемещения

При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения 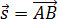(см.рис. 1.3).

Выберем ось ОХ так, чтобы вектор лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно А_x и В_x. Длина отрезка А_xВ_x на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть

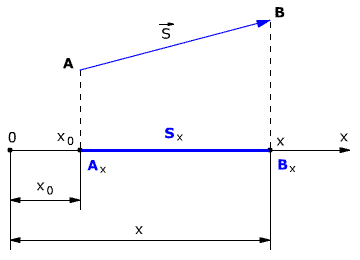
Рис. 1.3. Проекция вектора перемещения.

Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть

Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:

Здесь x₀, y₀, z₀ — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).

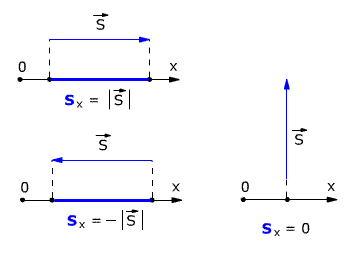
Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).

Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).

Рис. 1.4. Модули проекции вектора перемещения.

Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.

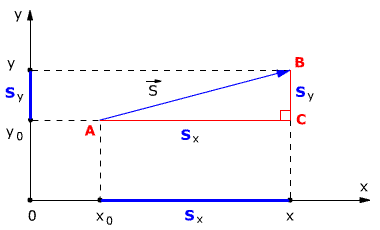
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х₀ и у₀, то есть А(х₀, у₀). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.

Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).

Рис. 1.5. Движение тела на плоскости.

Определим проекции вектора перемещения на осях ОХ и OY:

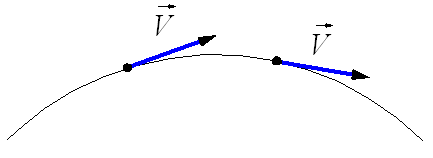
На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как

По теореме Пифагора

Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:

Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.

Источник

Криволинейное движение – формула, примеры, признаки

Если на тело не действуют внешние силы, оно движется равномерно и прямолинейно. Однако, большинство тел в природе находятся во взаимодействии с другими телами, поэтому наиболее частым видом движения является криволинейное. Рассмотрим особенности такого движения.

Описание криволинейного движения

Движение, траектория которого не является прямой линией, называется криволинейным. Примерами криволинейного движения могут являться вращение частей двигателей, колес, дрожание листвы на ветру, полет камня, брошенного под углом к горизонту, и многое другое.

Рис. 1. Криволинейное движение в природе.

Криволинейное движение – это значительно более сложное движение по сравнению с прямолинейным. При прямолинейном движении происходит изменение модулей векторов перемещения, скорости и ускорения. Их направления всегда параллельны вектору перемещения. Если же движение криволинейно, то изменяются не только модули, но и направления. Фактически, изменения направлений векторов перемещения и скорости – это главные признаки криволинейного движения.

Первым методом исследования криволинейного движения является проецирование на координатные оси. Проецированное движение является прямолинейным, и к нему можно применять законы прямолинейного движения.

Вторым методом является разбиение всей траектории пути на короткие участки, каждый из которых неограниченно приближается к прямолинейному, таким образом, в качестве формул криволинейного движения становится возможным использовать формулы прямолинейного движения.

Скорость при криволинейном движении

Перемещение – это вектор от начала рассматриваемой траектории до ее конца. При прямолинейном движении этот вектор одновременно является и траекторией движения, а направление вектора скорости совпадает с направлением вектора перемещения.

При криволинейном движении траектория длиннее вектора перемещения. Однако, чем короче вектор перемещения, тем меньше разница.

Таким образом, если разбить траекторию на много коротких отрезков, движение на каждом из них приблизится к прямолинейному. Направление скорости на каждом отрезке совпадет с направлением отрезка. По мере увеличения числа таких отрезков, каждый из них неограниченно стягивается в точку, имея направление, параллельное к касательной в этой точке.

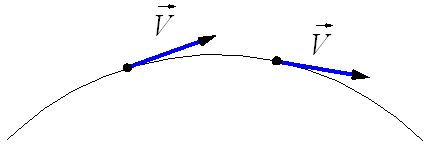
таким образом, мгновенная скорость криволинейного движения направлена по касательной к траектории движения.

Рис. 2. Мгновенная скорость криволинейного движения.

Ускорение при криволинейном движении

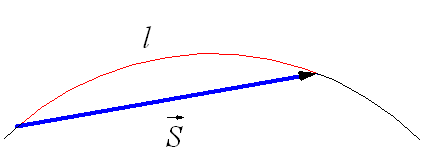
Ускорение – это мера изменения скорости. И если скорость прямолинейного движения постоянна, то и ускорение равно нулю. Для криволинейного движения скорость всегда изменяется. Модуль вектора скорости может оставаться постоянным, но из-за того, что вектор направлен всегда по касательной к траектории, а она не является прямой линией, направление этого вектора будет постоянно меняться. А если вектор скорости постоянно меняется (пусть не по модулю, а только по направлению), значит, при таком движении ускорение всегда присутствует.

Отметим, что если бы направление векторов скорости и ускорения в какой-то момент были бы одинаковыми, то в следующий момент скорость изменила бы только свой модуль, направление ее бы осталось прежним, траектория стала бы прямой линией, движение стало бы прямолинейным.

Криволинейное движение – это всегда движение с ускорением. Причем, направление вектора ускорения никогда не совпадает с направлением вектора скорости.

Рис. 3. Вектор ускорения при криволинейном движении.

Что мы узнали?

Криволинейное движение – это движение по траектории, которая не является прямой. Мгновенная скорость при криволинейном движении всегда направлена по касательной траектории. Ускорение при криволинейном движении всегда присутствует, и его направление всегда отличается от направления вектора скорости.

Источник

Криволинейное движение

Вы будете перенаправлены на Автор24

В зависимости от формы траектории, движение делится на прямолинейное и криволинейное. В реальном мире мы чаще всего имеем дело с криволинейным движением, когда траектория представляет собой кривую линию. Примерами такого движения является траектория тела, брошенного под углом к горизонту, движение Земли вокруг Солнца движение планет, конца стрелки часов по циферблату и т.д.

Рисунок 1. Траектория и перемещение при криволинейном движении

Рисунок 2. Мгновенная скорость при криволинейном движении

Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).

Для исследования криволинейного движения материальной точки применимы два разных подхода.

Можно разбить движение на отдельные участки, на каждом из которых движение можно считать прямолинейным (рис. 3).

Рисунок 3. Разбиение криволинейного движения на поступательные движения

А дальше на каждом из этих участков мы можем пользоваться законами прямолинейного движения, которые мы уже знаем. В принципе, такой подход возможен.

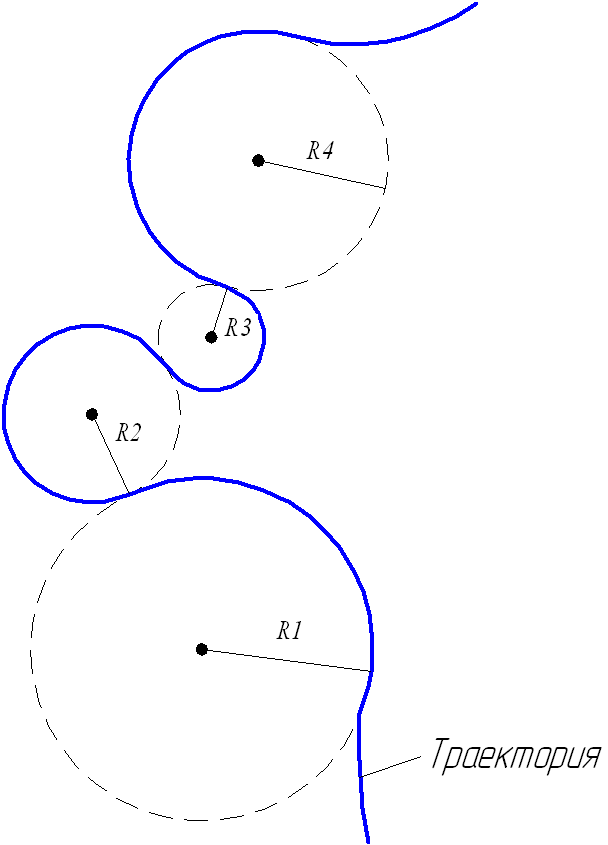
Однако более удобным является следующий подход. Можно представить это движение как совокупность нескольких движений по дугам окружностей (см. рис. 4.). Таких разбиений получится меньше, чем в предыдущем случае, кроме того, движение по окружности само является криволинейным.

Рисунок 4. Разбиение криволинейного движения на движения по дугам окружностей

Готовые работы на аналогичную тему

Для того, чтобы описывать криволинейное движение, нужно научиться описывать движение по окружности, а потом произвольное движение представлять в виде совокупностей движений по дугам окружностей.

Задачей исследования криволинейного движения материальной точки является составление кинематического уравнения, описывающего это движение и позволяющего по заданным начальным условиям определить все характеристики этого движения.

Центры окружностей лежат на одной прямой, поэтому

Траектория представляет собой сумму полуокружностей:

Источник

Криволинейное движение

Криволинейное движение. Движение по окружности. Угловая скорость. Период и частота обращения. Ускорение тела при движении по окружности. Тангенциальное и нормальное ускорение.

Криволинейное движение — механическое движение, траектория которого — кривые линии с произвольным ускорением и произвольной скоростью.

Движение тела по окружности — частный случай криволинейного движения.

Угловая скорость — величина, характеризующая скорость вращения материальной точки вокруг центра вращения. \[\fbox <$\omega=\dfrac\varphi t=\dfrac<2\pi>$>\]

Единицы измерения: \(\displaystyle [\frac<\text<рад>>]\) (радиан в секунду).

Период обращения — это время одного полного оборота.

Единицы измерения: \(\displaystyle [\text]\) (секунда)

Частота обращения — это величина, обратная периоду. Частота показывает, сколько полных оборотов совершает материальная точка за секунду. \[\fbox <$\nu=\dfrac1T$>\]

Единицы измерения: \(\displaystyle [\text<об>/\text<с>]\) (оборот в секунду), \(\displaystyle [\text<Гц>]\) (Герц).

Тангенциальное ускорение — компонента ускорения, направленная по касательной к траектории движения.

Единицы измерения: \(\displaystyle [\text<м>/\text<с>^2]\) (метр в секунду за секунду).

Нормальное (центростремительное) ускорение — компонента ускорения, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной, направленное к центру кривизны траектории. \[\fbox<$a_\text<цс>=\dfrac$>\] Единицы измерения: \(\displaystyle [\text<м>/\text<с>^2]\) (метр в секунду за секунду).

Полное ускорение тела, движущегося по окружности равно векторной сумме тангенциального и нормального ускорений. \[\fbox<$\overrightarrow a_\text<полн>=\overrightarrow a_\text<тан>+\overrightarrow a_\text<цс>$>\]

Источник