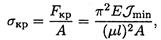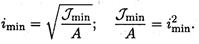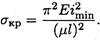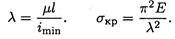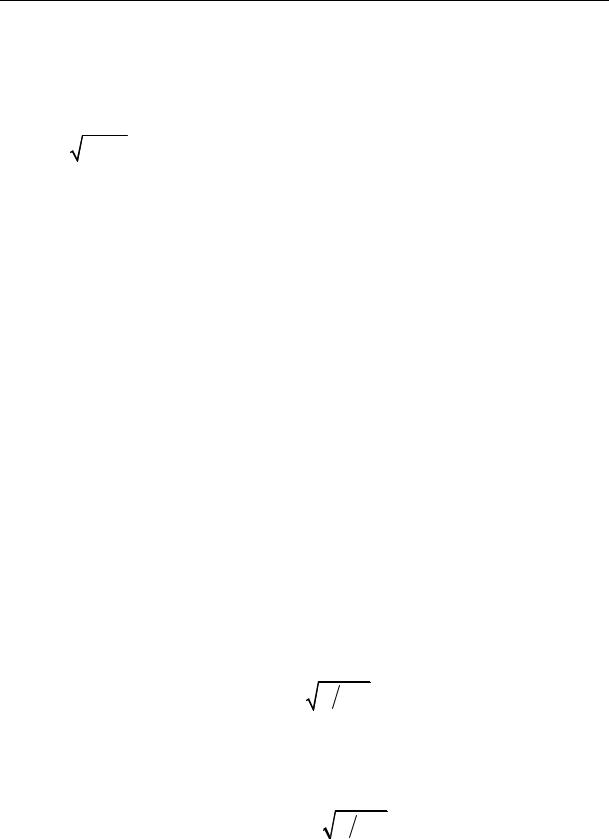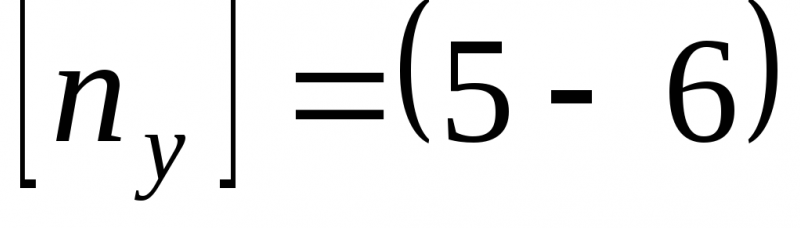что такое критическое напряжение
Критическое напряжение. Расчет колонн



Критическое напряжение. Расчет колонн
Принимая во внимание случай стойки с шарнирным концом, получим критическое напряжение путем деления критической нагрузки, определяемой по формуле (145), на площадь поперечного сечения. Найдите его таким образом ® кг / см2, Wr соединение с ОКР в случае стали.
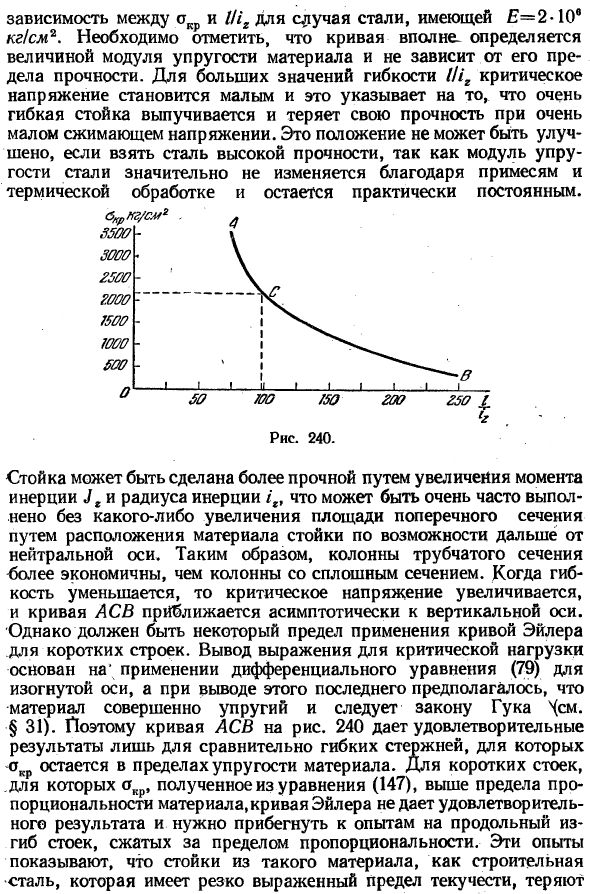
Отметим, что кривая полностью определяется модулем упругости материала и не зависит от его прочности на растяжение. При большом значении гибкости 1 НГ критическое напряжение мало, что указывает на то, что очень гибкая стойка выпячивается и теряет свою прочность при очень малом напряжении сжатия. Это положение не может быть улучшено, если используется высокопрочная сталь.
Это объясняется тем, что модуль упругости стали существенно не изменяется из-за примесей или термической обработки и остается практически постоянным. Стенд можно сделать более прочным за счет увеличения момента инерции Jr и радиуса инерции. Это можно сделать без увеличения площади поперечного сечения, поместив материал на подставку как можно дальше от нейтральной оси.
Поэтому колонны трубчатого сечения более экономичны, чем колонны непрерывного сечения columns. As гибкость уменьшается, критическое напряжение увеличивается, и кривая ASB приближается к вертикальной оси асимптотически. Однако существуют некоторые ограничения на применение кривых Эйлера с короткими структурами.
Вывод формулы критической нагрузки основан на применении дифференциальных уравнений (79) к оси кривой, и если это выводит последнее, то предполагалось, что материал полностью упруг и подчиняется закону хукена нема. § 31).Таким образом, Диа-кривая на рисунке равна 240, что дает удовлетворительный результат только для относительно гибких стержней, где ОКР находится в пределах упругого диапазона материала.
Если площадь, полученная из уравнения (147), является более короткой стойкой выше пропорционального предела материала, кривая Эйлера не даст удовлетворительных результатов, и необходимо прибегнуть к экспериментам вертикального изгиба на стойках, которые были сжаты за пропорциональным пределом. Людмила Фирмаль
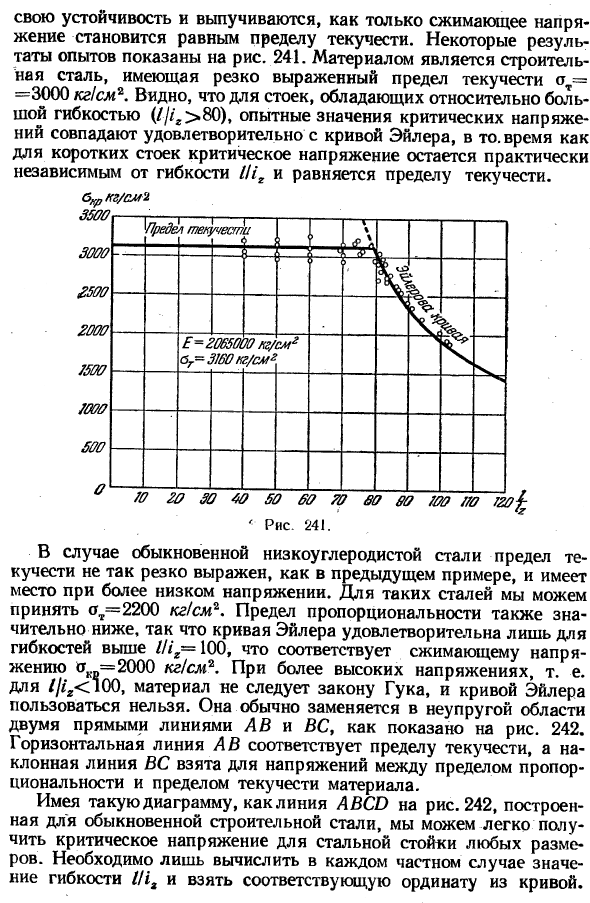
Эти эксперименты показывают, что как только напряжение сжатия становится равным пределу текучести, стеллажи из таких материалов, как строительная сталь, которые имеют ярко выраженный предел текучести, теряют свою устойчивость и разбухают. Некоторые экспериментальные результаты представлены на рисунке. 241.
Материал структурная сталь и имеет замечательную прочность выхода от= 3000 kg1cm2.В относительно гибкой стойке (/•//*>80), вы можете видеть, что экспериментальное значение критического напряжения на самом деле хорошо соответствует кривой Эйлера. С другой стороны, для коротких стоек критическое напряжение практически не зависит от гибкости Wr и равно пределу текучести. — Рисунок 241.
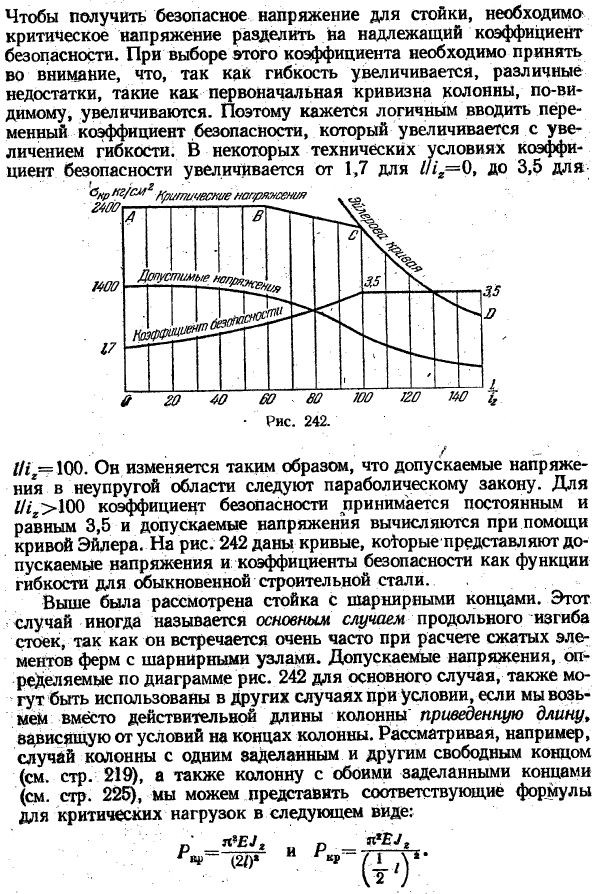
Для обычных низкоуглеродистых сталей предел текучести не так выражен, как в предыдущем примере, и он возникает при низких напряжениях. За такую сталь можно взять= 2200 кг! См2. Пропорциональный предел также намного ниже, поэтому кривая Эйлера равна a = 2000 кг! Это удовлетворительно только для гибкости, которая превышает W-100, что соответствует напряжению сжатия Cm2.At при более высоком напряжении, то есть///, 100 коэффициент запаса прочности принимается равным 3,5, а допустимое напряжение рассчитывается с использованием кривой Эйлера.
На рисунках приведены 242 кривые, которые представляют собой допустимые напряжения и коэффициент запаса прочности в зависимости от гибкости обычной строительной стали. Выше была рассмотрена стойка с шарнирами на обоих ends. In этот случай иногда называют основным случаем продольного изгиба вертикального материала, так как он очень распространен при расчете элементов сжатия ферм с шарнирными узлами.
Вместо фактической длины допустимого напряжения столба, как определено на рисунке на рисунке, 242 может также использоваться для основного случая, при условии, что длина уменьшается в 2 раза от размера условия в конце столбца. Например, формула, соответствующая критической нагрузке, может быть представлена в следующем виде с учетом случая колонны, в которой один конец запечатан, а другой конец открыт (см. стр. 219), а другой конец запечатан (см. стр. 225).: п л * ejt не п _ «*>(2/) * » П / Я Д4 *
Если сравнить эти формулы с формулой основного случая (145), то можно сделать вывод, что если вычислить столбец, в котором один вложен, а другой является свободным концом, то для использования фигуры 242 нам потребуется в 2 раза больше фактической длины. Для колонки с обоими загерметизированными концами, укороченная длина половина фактической длины. Людмила Фирмаль
Выбор соответствующих размеров поперечного сечения колонны обычно производится путем последовательных испытаний. Поскольку мы знаем нагрузку P, которая действует на колонну, мы берем некоторые размеры сечения и вычисляем Jg и UiK для этих размеров. Значение безопасного напряжения сжатия затем берется из диаграммы. 242.
Если это значение умножить на допустимую площадь поперечного сечения, то получается допустимая нагрузка на колонну. Если эта нагрузка не падает ниже P и немного больше, то допустимое сечение удовлетворительно. В противном случае расчет придется повторить. Если торцом является герметичная колонна, то при расчете ix учитывается общее поперечное сечение. это связано с тем, что отверстия в заклепке существенно не влияют на критическую нагрузку.
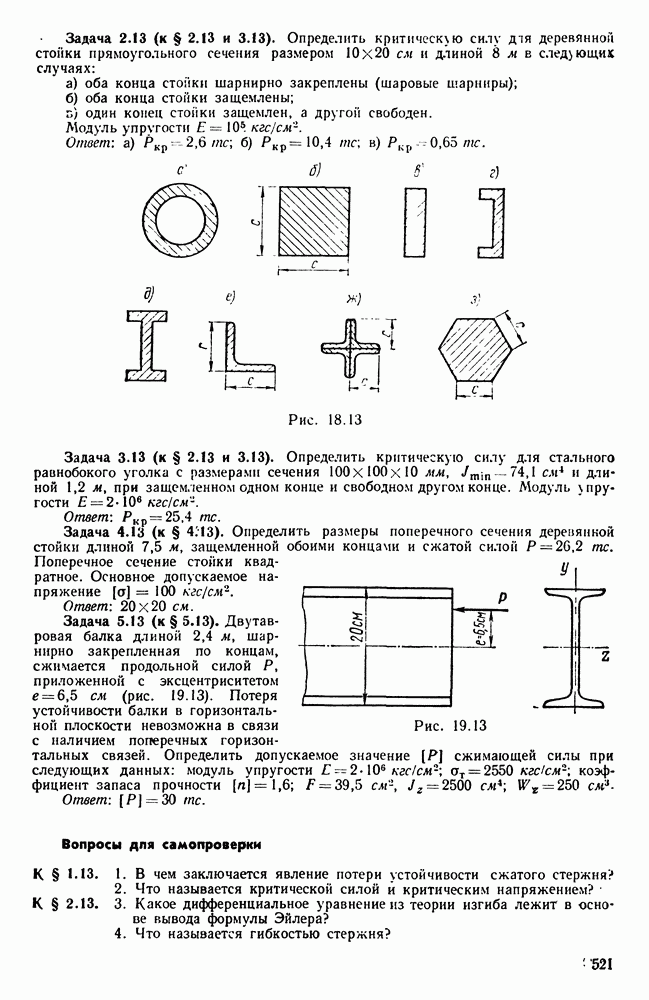
Однако при расчете безопасной нагрузки на колонну допустимое напряжение умножается на площадь чистого поперечного сечения, чтобы гарантировать отсутствие чрезмерного напряжения в колонне. Задачи 1.Стальной стержень с прямоугольным поперечным сечением 2,5 х см, концы которого соединены, сжимается под действием продольной силы.
Если предел пропорциональности материала составляет 2000 кг / см *и Е = * = 2•10 кг / см2, то определяют самую короткую длину, которую формула (147) может применить к критическому напряжению. Если длина стержня составляет 1,5 м, определите критическое значение напряжения. Ответ. Минимальная длина составляет » 72 см.«/Критическое напряжение составляет » 1,5 л. 457 кг / см2. 。 2.
Решаем предыдущую задачу, предполагая, что стержень имеет круглое поперечное сечение диаметром 2,5 см, а концы герметизированы. 3.Длина. Определить критическое / сжимающее напряжение балки двутаврового сечения, равной 1,8 м и герметизированной с обоих концов. «=64,4 см€, Jy= 712 см, F » 21,5 см2.
Используйте кривые рисунка для определения безопасной нагрузки. 242. Ответ. АКО = 1830 кг / см2,///, «104, безопасная нагрузка» = 11,240 / С Р 4.Решите предыдущую задачу, предположив, что края колонны герметичны. Воспользуйтесь фотографиями. 242. Ответ. ОКР = «2200 кг / см*, коэффициент запаса» = 2, безопасность нагрузка= 23 650 кг. Рисунок 243. 5.
Используйте диаграмму для расчета. 242 безопасная нагрузка Для стержня (рис.243), состоящего из 2 двутавровых балок с тем же поперечным сечением, что и в задаче 3 выше. Длина стержня составляет 3 л, с шарнирным концом. Предположим, что соединение очень жесткое, и оба двутавровых луча работают как 1 Луч. Решение. Y * = 2X 712 = 1424 cl4,= 2 [64,4 + 21,5 X (5) 2] = 1204 см *.
Поэтому большое значение гибкости >-300 −567 ул, гш ’» Г 2-21. Пять На рисунке показано, что допустимое напряжение сжатия 242 составляет 1030 кг / см2. Предохранительная нагрузка= 1030 * 2.21.5 = 44 300 кг 6.Мы решаем предыдущую задачу, предполагая, что оба конца стержня герметичны. 7.Шарнирная колонна длиной 3G состоит из 2 каналов JZ = 53,2 см4, Y» = 563,7 см4, T7 = 18,51 см2, центра тяжести и расстояния r0 = 1 между наружной поверхностью стенки канала. 71 см.
Если расстояние между наружными поверхностями стенок канала составляет 10 см, найдите безопасную нагрузку в колонне. 8.Если нагрузка равна Р = 16 т, а оба конца закреплены шарниром, Определите необходимое квадратное сечение стальной стойки длиной 1,8 м. воспользуйтесь фотографиями. 242. 9.It решает предыдущую проблему, предполагая, что оба конца стойки запечатаны.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Критические напряжения



Критическое напряжение — напряжение сжатия, соответствующее критической силе.
Напряжение от сжимающей силы определяется по формуле
где σкр — напряжение сжатия, при котором стержень еще устойчив. Корень квадратный из отношения минимального момента инерции сечения к площади поперечного сечения принято называть минимальным радиусом инерции iт;п:
Тогда формула для расчета критического напряжения перепишется в виде
Отношение μl/imin носит название гибкости стержня λ.
Гибкость стержня — величина безразмерная, чем больше гибкость, тем меньше напряжение:
Заметим, что гибкость не зависит от материала, а определяется только геометрией стержня.
15.5. Критическое напряжение. Гибкость стержня
И. В. Богомаз. Механика
где i x = J x 
где λ – гибкость стержня, безразмерная геометрическая характеристика, определяемая размерами стержня и способом его закрепления.
Окончательно формула для критического напряжения выглядит
При выводе формулы Эйлера была использована зависимость (15.2), полученная на основе закона Гука. Отсюда следует, что формула Эйлера справедлива лишь в пределах применимости закона Гука, т. е. при условии, что критическое напряжение не превышает предела пропорциональности материала стержня:
Отсюда значение гибкости, которое соответствует этому условию, составляет
Величину, стоящую в правой части этого неравенства, обозначим λ пред и назовем предельной гибкостью
Предельная гибкость зависит только от механических свойств материала и имеет постоянное значение. Так для стали марки ВСт3 при
15. Устойчивость сжатых стержней
E = 2,06 10 5 МПа и σ pr = 200–210 МПа по формуле (15.20) λ пред ≈ 100 ;
т. е. формула Эйлера применима только к упругим стержням, когда гибкость стержня больше или равна предельной гибкости для материала, из которого он изготовлен.
Стержни, для которых выполняется условие (15.21), называются стержнями большой гибкости.
15.6. Продольный изгиб за пределом пропорциональности. Формула Ясинского
пользование формулы Эйлера для стержней, теряющих устойчивость за пределом упругости, является недопустимым.
Теоретическое решение задачи об устойчивости за пределом пропорциональности сложно, поэтому обычно пользуются эмпирическими формулами, полученными в результате обработки большого количества опытных данных.
Наиболее простой является линейная зависимость, предложенная в начале ХХ в. немецким ученым Л. Тетмаером и независимо от него профессором Петербургского института инженеров путей сообщения Ф. С. Ясинским:
где a и b – эмпирические коэффициенты, зависящие от материала стержня и имеющие размерность напряжения. Например, для стали марки ВСт3 их значения таковы: а = 310 МПа, b = 1,14 МПа.
Для чугуна пользуются параболической зависимостью
И. В. Богомаз. Механика
Соответствующая критическая сила по формуле Ясинского находится так:
Тогда условие применимости формулы Ясинского можно записать в виде
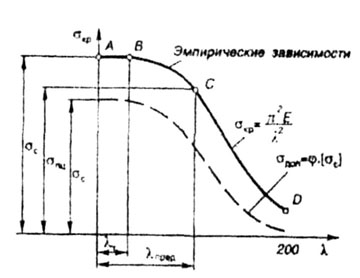
15.7. Диаграмма критических напряжений
В зависимости от гибкости сжатые стержни делятся на три категории:
1. Стержни большой гибкости (λ ≥ λ пред ), для которых расчет ведется по формуле Эйлера. В системе координат σ cr – λ зависимость
σ cr = π 2 2 E может быть представлена гиперболической кривой.
2. Стержни средней гибкости (λ 0 ≤ λ ≤ λ пред ) рассчитываются на устойчивость по эмпирической формуле Ясинского (15.22). Для них зависимость линейна:
15. Устойчивость сжатых стержней
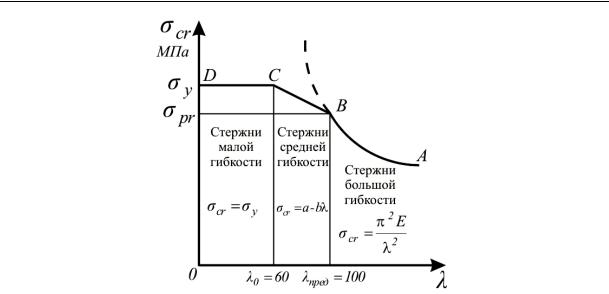
На рис. 15.6 показана диаграмма зависимости критических напряжений от гибкости сжатого стержня для стали ВСт3, которая состоит из трех частей:
• гиперболы Эйлера АВ при λ ≥ 100;
• наклонной прямой Ясинского ВС при 60 ≤ λ • горизонтальной прямой CD при λ 0 100 стержень теряет устойчивость в упругой стадии. Для значений λ ВС ). Горизонтальная прямая CD соответствует напряжению, равному пределу текучести.
Применение формул Эйлера и Ясинского позволяет решать задачи устойчивости сжатых стержней на всем интервале значений гибкостей, которые встречаются в строительной практике.
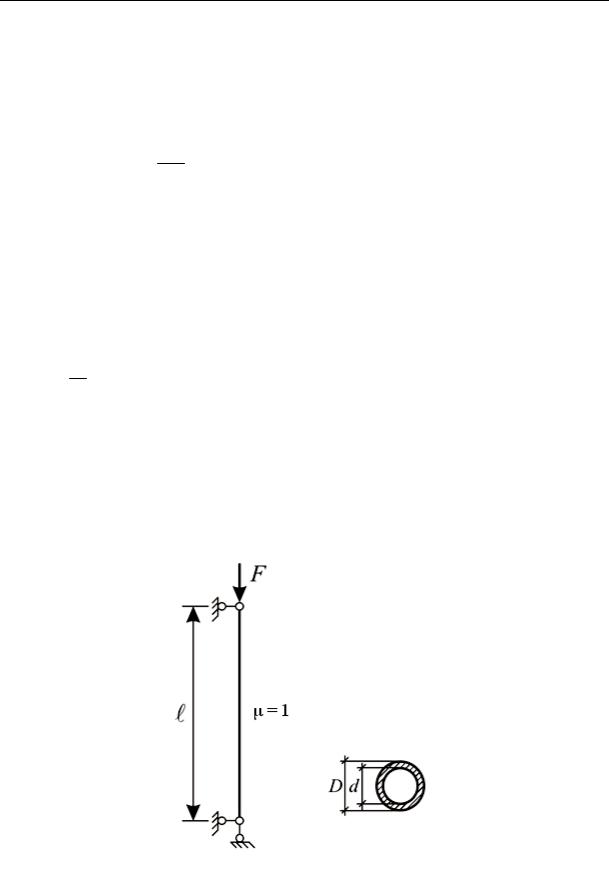
Пример 15.1. Стальной стержень круглого трубчатого сечения D = 10 см и d = 7 см при длине = 3, 2 м имеет шарнирно закрепленные
И. В. Богомаз. Механика
Материал стержня – сталь марки ВСт3 с пределом пропорциональности σ pr = 210 МПа и модулем упругости E = 2 10 5 МПа.
формулудлякоторойвыберемвзависимостиотгибкостистержня. Определяем геометрические характеристики поперечного сече-
• осевой момент инерции сечения относительно любой оси
J = π 64 D 4 ( 1 −α 4 ) = π 64 10 4 ( 1 − 0,7 4 ) = 373 см 4 ;
Что такое критическая сила
ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ. КРИТИЧЕСКАЯ СИЛА
В
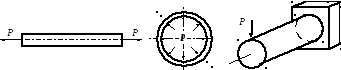
этих примерах с увеличением нагрузки
вплоть до разрушения стержень останется
прямым, кольцо – круглым, балка –
изгибаться по одному и тому же уравнению.
Форма равновесия не зависит от величины
внешней силы. Это – устойчивые деформации.
В этих примерах
форма равновесия зависит от величины
силы. Это – неустойчивая форма деформации.
Под
устойчивостью понимают свойство упругой
системы сохранять под нагрузкой
первоначальную форму упругого равновесия.
Потеря
устойчивости наблюдается в элементах
конструкций, работающих на сжатие.
Например, устойчивость может потерять
стенка двутавровой балки при изгибе,
труба, нагруженная внешним давлением,
корпус подводной лодки, корабельный
гребной вал, ходовой винт металлорежущего
станка и т.д.
Остановимся
на изучении наиболее простой формы
потери устойчивости – стержень, сжатый
вдоль продольной оси.
1. Устойчивая форма упругого равновесия.
Стержень, получив малое отклонение,
вновь возвращается в исходное положение.






2.
Безразличная форма упругого равновесия.
Стержень, получив малое отклонение,
сохраняет состояние покоя. Сила,
соответствующая безразличному состоянию,
называется критической силой, а напряжения
– критическими напряжениями.
3.
Неустойчивая форма равновесия. Стержень,
получив малое отклонение, не возвращается
обратно, а продолжает изгибаться. Прогибы
бытро нарастают, наступает разрушение.
Сила
Ркр
является опасной нагрузкой. Поэтому
нужно иметь некоторый запас по
устойчивости. Введём понятие допускаемой
силы 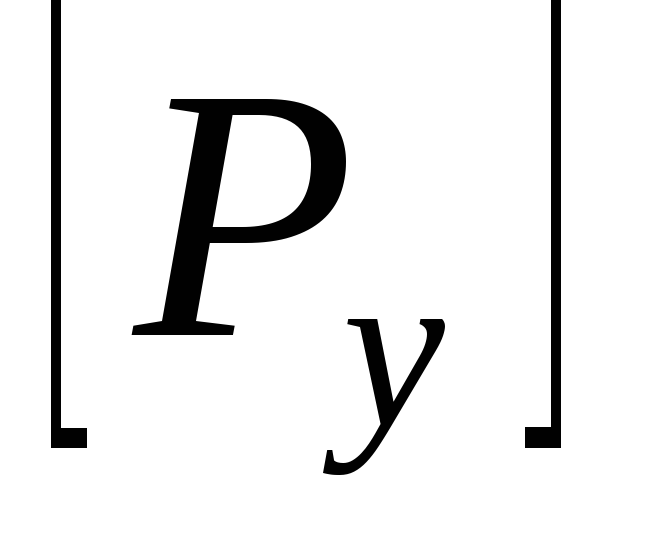
и напряжения.

;
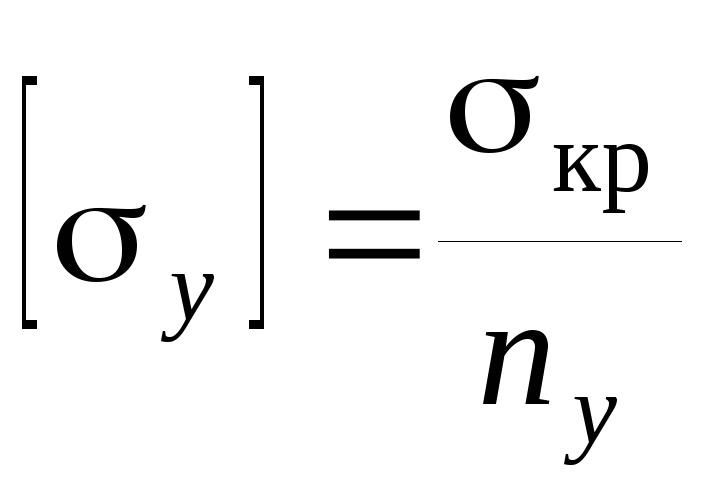
, где 
— коэффициент запаса устойчивости.

– строительные
конструкции

– машиностроение
для
чугунов
Изгиб стержня,
связанный с потерей устойчивости,
называют продольным изгибом.
Формула
Л. Эйлера для критической силы (1744 г.)

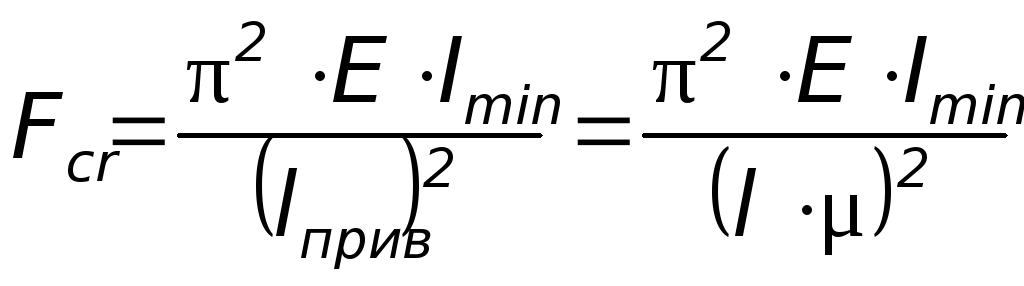
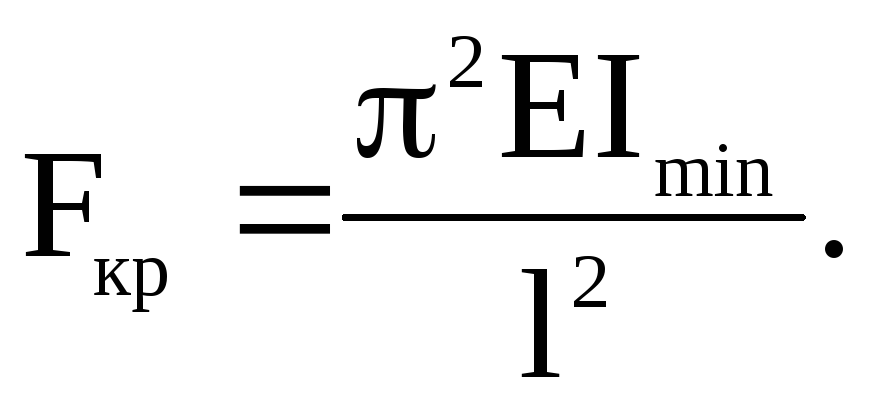
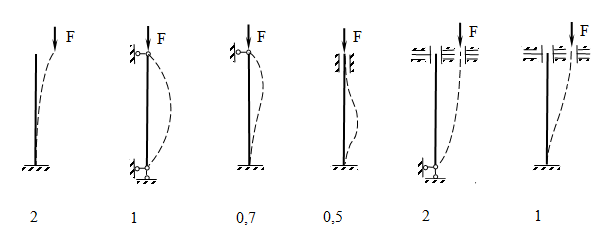




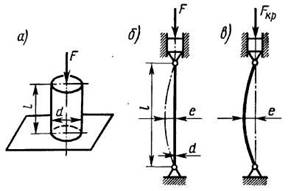
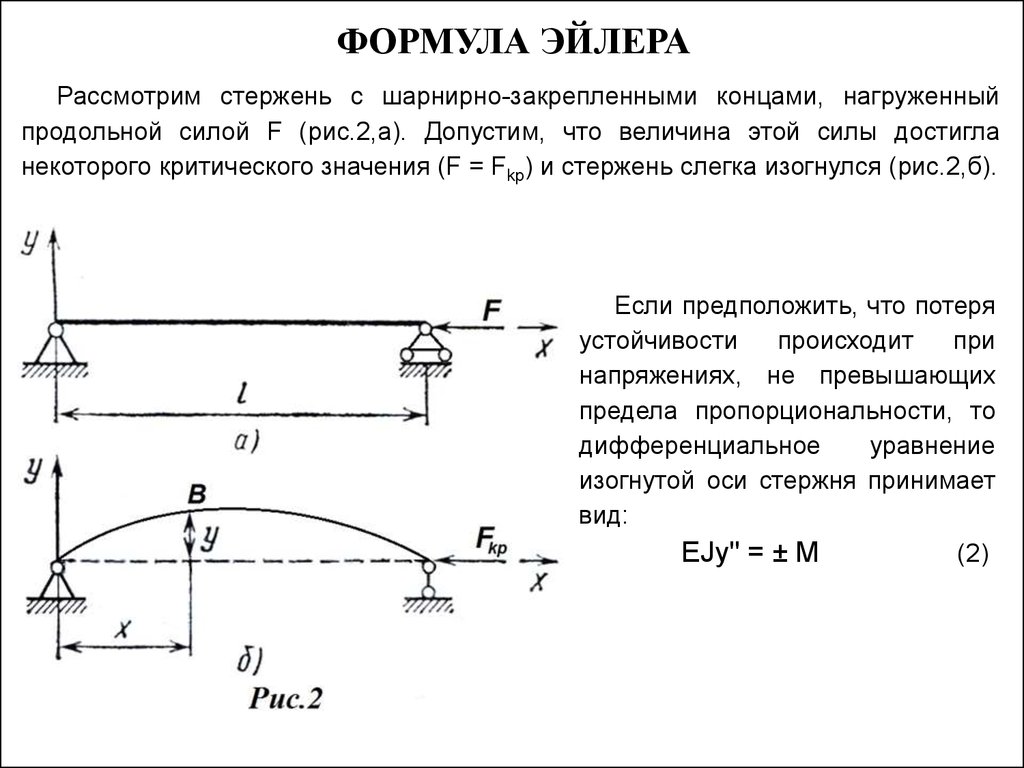
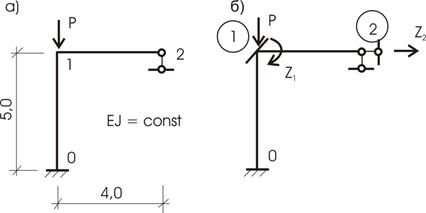
Рассмотрим
стержень длиной l
, на шарнирных опорах сжатый продольной
силой Ркр
.
Доказано,
что упругая линия такого стержня
представляет собой синусоиду.
Величина
силы Ркр
вычисляется по формуле Л. Эйлера (даётся
без вывода)

(1)
где 
– наименьший из двух моментов инерции
поперечного сечения стержня.
l
– длина
полуволны синусоиды упругой линии (в
нашем случае – длина стержня).
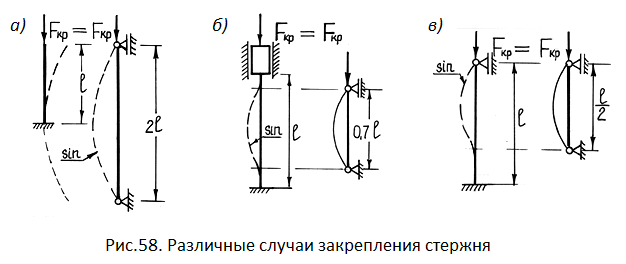
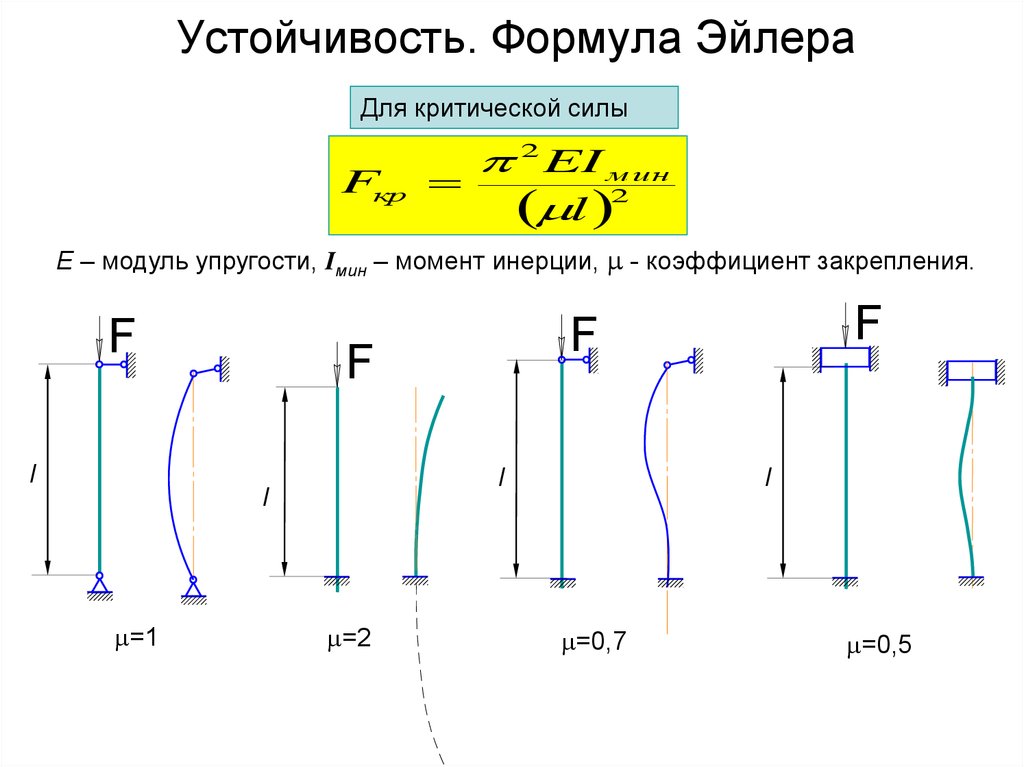
Формулу
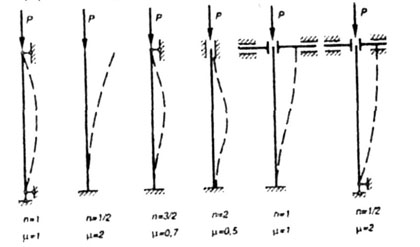
(1) можно распространить на другие способы
крепления концов стержня, при которых
длина полуволны будет другой. Тогда
формула Л. Эйлера примет вид:

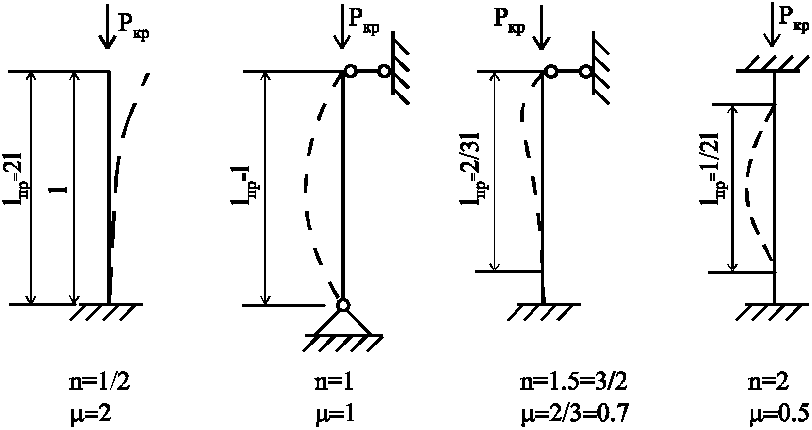
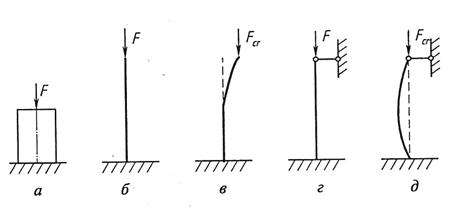





(2)
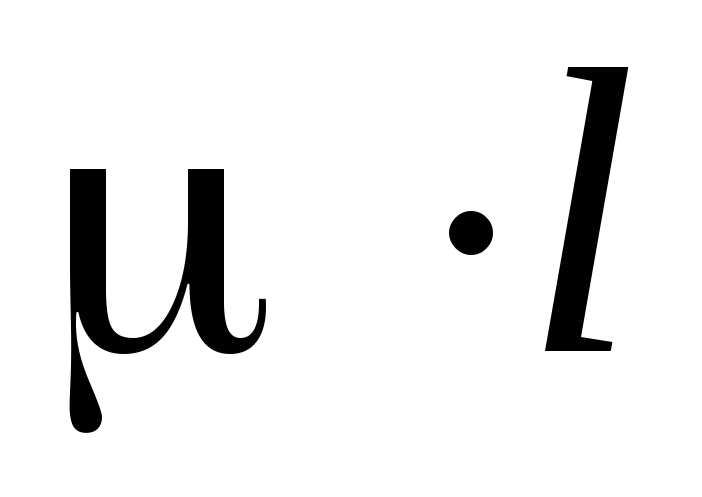
– приведенная длина стержня ;

– коэффициент
приведения длины стержня, зависящий от
способа крепления его концов (введён
Ясинским).
Из
формулы (2) видно, что критическая сила 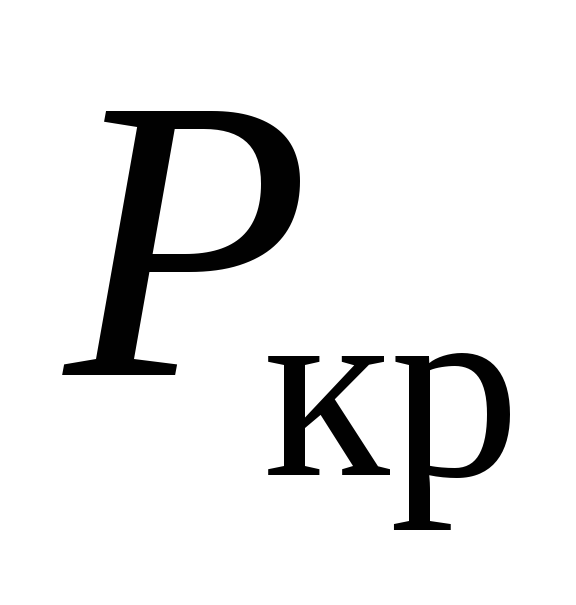
не зависит от характеристик прочности
материала 
и 
Поэтому при большой гибкости стержня,
когда “работает”
формула
Л. Эйлера, не имеет смысла применять
дорогие легированные стали, а наоборот,
следует использовать самые дешёвые
материалы с низкими прочностными
свойствами, т.к. 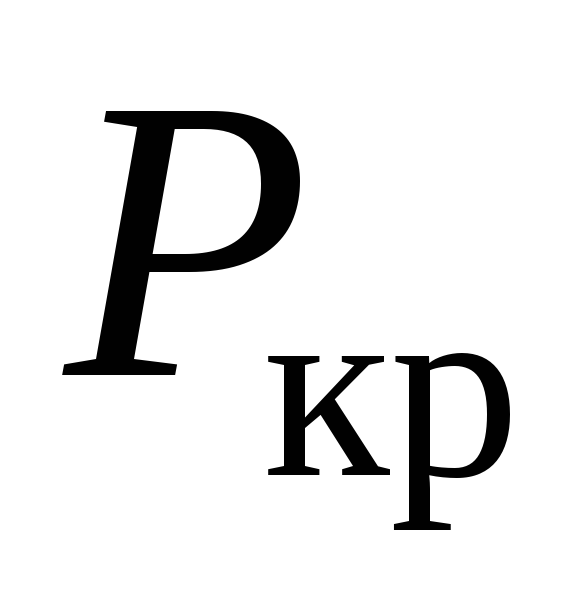
зависит только от модуля Юнга Е,
который для всех сталей примерно одинаков
(Е
= 2·105
МПа).
Пределы
применимости формулы Эйлера.
Критические
напряжения по Эйлеру. Гибкость стержня.

– напряжение
от действия 

называют минимальным радиусом инерции
сечения.
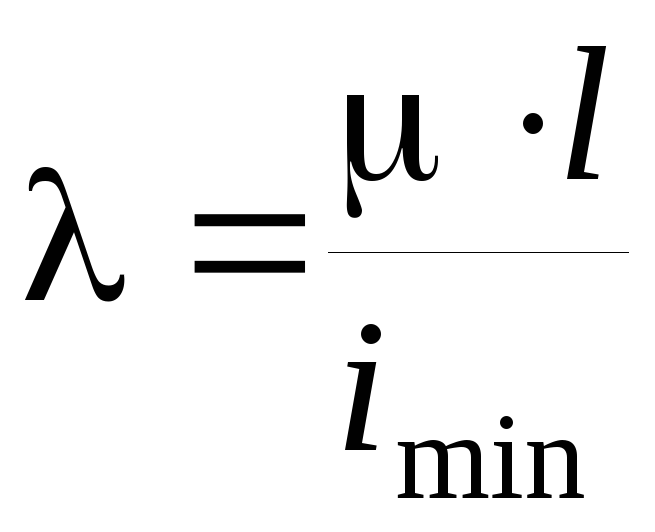
– гибкость стержня.

т.е. 
(3)






Из
формулы (3) видно, что с уменьшением
гибкости величина
растёт.