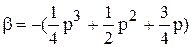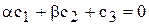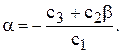что такое критерий устойчивости
Критерии устойчивости (Лекция)
2. Корневой критерий
3. Критерий Стодолы
4. Критерий Гурвица
5. Критерий Михайлова
6. Критерий Найквиста
7. Показатели качества
8. Прямые показатели качества
9. Корневые показатели качества
10. Частотные показатели качества
Важным показателем АСР является устойчивость, поскольку основное ее назначение заключается в поддержании заданного постоянного значения регулируемого параметра или изменение его по определенному закону. При отклонении регулируемого параметра от заданной величины (например, под действием возмущения или изменения задания) регулятор воздействует на систему таким образом, чтобы ликвидировать это отклонение. Если система в результате этого воздействия возвращается в исходное состояние или переходит в другое равновесное состояние, то такая система называется устойчивой. Если же возникают колебания со все возрастающей амплитудой или происходит монотонное увеличение ошибки е, то система называется неустойчивой.
Для того, чтобы определить, устойчива система или нет, используются критерии устойчивости:
1) корневой критерий,
2) критерий Стодолы,
3) критерий Гурвица,
4) критерий Найквиста,
5) критерий Михайлова и др.
Первые два критерия являются необходимыми критериями устойчивости отдельных звеньев и разомкнутых систем. Критерий Гурвица является алгебраическим и разработан для определения устойчивости замкнутых систем без запаздывания. Последние два критерия относятся к группе частотных критериев, поскольку определяют устойчивость замкнутых систем по их частотным характеристикам. Их особенностью является возможность применения к замкнутым системам с запаздыванием, которыми является подавляющее большинство систем управления.
2. Корневой критерий
Корневой критерий определяет устойчивость системы по виду передаточной функции. Динамической характеристикой системы, описывающей основные поведенческие свойства, является характеристический полином, находящийся в знаменателе передаточной функции. Путем приравнивания знаменателя к нулю можно получить характеристическое уравнение, по корням которого определить устойчивость.
Корни характеристического уравнения (они обозначены звездочкой) могут быть как действительные, так и комплексные и для определения устойчивости откладываются на комплексной плоскости.
Виды корней характеристического уравнения:
положительные (корень № 1);
комплексные сопряженные (4);
По кратности корни бывают:
сопряженные (4, 5): si = a ± j w ;
Корневой критерий формулируется следующим образом:
Линейная АСР устойчива, если все корни характеристического уравнения лежат в левой полуплоскости. Если хотя бы один корень находится на мнимой оси, которая является границей устойчивости, то говорят, что система находится на границе устойчивости. Если хотя бы один корень находится в правой полуплоскости (не зависимо от числа корней в левой), то система является неустойчивой.
Иными словами, все действительные корни и действительные части комплексных корней должны быть отрицательны. В противном случае система неустойчива.
Пример 4.1. Передаточная функция системы имеет вид:

Характеристическое уравнение: s 3 + 2 s 2 + 2.25 s + 1.25 = 0.
Следовательно, система устойчива.
3. Критерий Стодолы
Этот критерий является следствием из предыдущего и формулируется следующим образом: Линейная система устойчива, если все коэффициенты характеристического полинома положительны.
То есть, для передаточная из примера 4.1 по критерию Стодола соответствует устойчивой системе.
4. Критерий Гурвица
Критерий Гурвица работает с характеристическим полиномом замкнутой системы. Как известно, структурная схема АСР по ошибке имеет вид, как показано на рисунке ниже.
Далее с учетом наличия отрицательной обратной связи получаем передаточную функцию замкнутой системы:

Как правило, передаточная функция разомкнутой системы имеет дробно-рациональный вид:

Тогда после подстановки и преобразования получаем:

Отсюда следует, что характеристический полином замкнутой системы (ХПЗС) можно определить как сумму числителя и знаменателя W ¥ :
D з( s ) = A ( s ) + B ( s ).
Для определения устойчивости по Гурвицу строится матрица таким образом, чтобы по главной диагонали были расположены коэффициенты ХПЗС с an +1 по a 0. Справа и слева от нее записываются коэффициенты с индексами через 2 ( a 0, a 2, a 4… или a 1, a 3, a 5 …). Тогда для устойчивой системы необходимо и достаточно, чтобы определитель и все главные диагональные миноры матрицы были больше нуля.
Если хотя бы один определитель будет равен нулю, то система будет находится на границе устойчивости.
Если хотя бы один определитель будет отрицателен, то система неустойчива не зависимо от числа положительных или нулевых определителей.
Пример. Дана передаточная функция разомкнутой системы

Для этого определяется ХПЗС :
D(s) = A(s) + B(s) = 2s 4 + 3s 3 + s 2 + 2s 3 + 9s 2 + 6s + 1 = 2s 4 + 5s 3 + 10s 2 + 6s + 1.
Поскольку степень ХПЗС равна n = 4, то матрица будет иметь размер 4х4. Коэффициенты ХПЗС равны а4 = 2, а3 = 5, а2 = 10, а1 = 6, а0 = 1.
(обратите внимание на сходство строк матрицы: 1 с 3 и 2 с 4). Определители:

Поскольку все определители положительны, то АСР устойчива.
5. Критерий Михайлова
Описанные выше критерии устойчивости не работают, если передаточная функция системы имеет запаздывание, то есть может быть записана в виде

В этом случае характеристическое выражение замкнутой системы полиномом не является и его корни определить невозможно. Для определения устойчивости в данном случае используются частотные критерии Михайлова и Найквиста.
Порядок применения критерия Михайлова:
1) Записывается характеристическое выражение замкнутой системы:
2) Подставляется s = j w : D з (j w ) =Re( w ) + Im( w ).
3) Записывается уравнение годографа Михайлова D з( j w ) и строится кривая на комплексной плоскости.
Если годограф Михайлова проходит через начало координат, то говорят, что система находится на границе устойчивости.
6. Критерий Найквиста
Данный критерий аналогичен критерию Михайлова, но работает с АФХ системы, поэтому более сложен для расчетов.
1) Определяется передаточная функция разомкнутой системы 
3) Подставляется s = j w : W ¥ ( j w ).
4) Строится АФХ разомкнутой системы.
Если АФХ проходит через точку (-1; 0), то замкнутая система находится на границе устойчивости.
В случае, если характеристическое уравнение разомкнутой системы A ( s ) = 0 корней не имеет (т.е. m = 0), то критерий, согласно критерию, замкнутая система является устойчивой, если АФХ разомкнутой системы W ¥ ( j w ) не охватывала точку (-1; 0), в противном случае система будет неустойчива (или на границе устойчивости).
7. Показатели качества
Если исследуемая АСР устойчива, то может возникнуть вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям. На практике качество регулирования может быть определено визуально по графику переходной кривой, однако, имеются точные методы, дающие конкретные числовые значения.
Показатели качества разбиты на 4 группы:
8. Прямые показатели качества

Предположим, переходная кривая, снятая на объекте, имеет колебательный вид (см. рис. 1.38).
Сразу по ней определяется установившееся значение выходной величины ууст.
Степень затухания y определяется по формуле

Время достижения первого максимума t м определяется по графику.
9. Корневые показатели качества
Не требуют построения переходных кривых, поскольку определяются по корням характеристического полинома. Для этого корни полинома откладываются на комплексной плоскости и по ним определяются:
Степень устойчивости h определяется как граница, правее которой корней нет, т.е.
h = min 
m = min 
10. Частотные показатели качества
Для определения частотных показателей качества требуется построение АФХ разомкнутой системы и АЧХ замкнутой системы.
Запас D A определяется по точке пересечения АФХ с отрицательной действительной полуосью.
Для определения D j строится окружность единичного радиуса с центром в начале координат. Запас D j определяется по точке пересечения с этой окружностью.
По АЧХ замкнутой системы определяются показатели колебательности по заданию М и ошибке МЕ как максимумы соответственно АЧХ по заданию и АЧХ по ошибке.
Связи между показателями качества.Описанные выше показатели качества связаны между собой определенными соотношениями:




Критерии устойчивости
Критерий Гурвица. Проверка устойчивости по Гурвицу сводится к вычислению n определителей, которые составляются по следующему правилу:
По этому критерию система будет устойчивой, если все определители положительные.
Критерий Михайлова. Если в характеристическом уравнении системы заменим оператор p на jw, получим функцию комплексного переменного
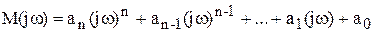
которая в комплексной плоскости определяет вектор
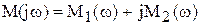
Этот вектор имеет следующее свойство. При изменении w от 0 до 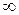
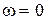
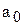
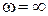
Согласно этому критерию линейная система n-го порядка будет устойчива, если годограф Михайлова охватывает начало координат и последовательно проходит n квадрантов, а в последнем квадранте уходит в бесконечность. Если годограф проходит через 0, то система находится на границе устойчивости.
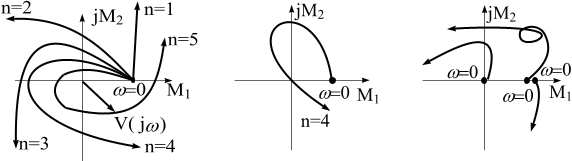 |
|
|
На рис. 6.3,а изображены годографы устойчивых систем с характеристическими уравнениями до пятой степени включительно. А на рис. 6.3,б приведены годографы неустойчивых систем.
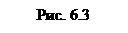 |
Критерий Найквиста. Этот критерий позволяет определить устойчивость системы по ее амплитудно-фазовым характеристикам, которые могут быть заданы как в аналитической форме, так и в виде опытных кривых. Особенностью критерия является то, что оценка устойчивости системы делается по характеристикам ее разомкнутого состояния. Это оказывается возможным благодаря однозначной зависимости между передаточной функцией разомкнутой системы и характеристическим уравнением этой системы в замкнутом состоянии.
Исследуемая система размыкается в любой точке, и аналитически или экспериментально определяется ее АФХ. Эта характеристика представляется комплексным уравнением 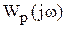
1) если разомкнутая система устойчива или нейтральна, то для устойчивости замкнутой системы необходимо и достаточно, чтобы характеристика 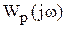
2) если разомкнутая система имеет m корней с положительной вещественной частью, то замкнутая система будет устойчивой только в том случае, если характеристика 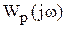
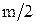
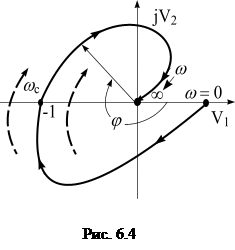
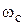
Если АФХ при частоте 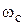
Если АФХ при частоте 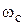
(-1, j0), то есть не охватывает ее, то амплитуда выходного сигнала на данной частоте меньше входного и находится в противофазе. В этом случае при замыкании системы амплитуда выходных колебаний будет затухать, то есть система будет устойчивой.
6.5. Определение областей устойчивости. D – разбиение
Постановка задачи.Выше были рассмотрены принципы исследования системы на устойчивость при условии, что все ее параметры уже заданы. Но часто при проектировании и наладке автоматических систем предоставляется свобода в выборе некоторых ее параметров. При этом представляет интерес такая технология выбора параметров, при которой обеспечивался бы необходимый запас устойчивости. Эта задача решается посредством выделения областей устойчивости в плоскости выбираемых параметров. Поясним физический смысл этих областей.
Положим, что автоматическая система имеет характеристическое уравнение
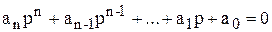

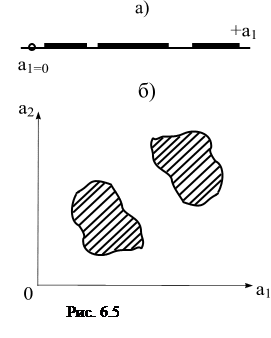
Положим теперь, что в уравнении (6.10) изменяются два коэффициента, например, 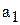
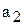
Обычно в практических задачах почти все параметры системы конструктивно заданы, и свобода выбора остается за одним или двумя параметрами. Поэтому задача выделения областей устойчивости практически сводится к построению границы в плоскости одного или двух параметров.
Алгоритм D-разбиенийоснован на использовании годографа Михайлова, который соответствует границе устойчивости, то есть годограф проходящий через начало координат.
D-разбиение по одному параметру.Представим характеристическое уравнение системы в виде
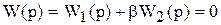
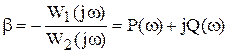
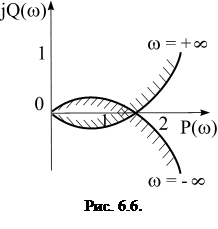
Кривая, построенная в системе координат Р(w), jQ(w) при различных значениях w, будет представлять границу D-разбиений. Область устойчивости находится слева от кривой, если двигаться по ней от значений 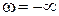
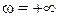
Так как параметр b является вещественным числом, то нас интересует отрезок только вещественной оси, попадающий в область устойчивости. Все значения параметра, определяемые координатами этого отрезка на оси абсцисс, окаймлённого штриховкой, будут соответствовать устойчивому состоянию системы.
Пример 6.1. Рассмотрим систему регулирования с характеристическим уравнением
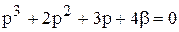
Решим характеристическое уравнение относительно b
и заменим в нем р на jw
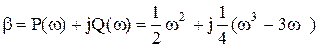
D-разбиение по двум параметрам.Представим характеристическое уравнение системы в виде
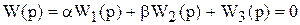
где a и b – свободные параметры системы. Заменим в уравнении р на jw и введем обозначения

Разделив (6.13) на вещественную и мнимую части, получим
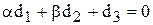
Решение этих уравнений даст интересующие нас параметры
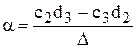
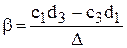
где 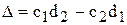
Если D ни при каких значениях w не обращается в нуль, то в плоскости a,b получаем кривую, являющуюся границей области устойчивости. Если D при каком-либо значении w обращается в нуль, то это может соответствовать двум случаям:
1) при D=0 числители выражений (6.15) не обращаются в нули; в этом случае переход D через нуль может произойти только в бесконечно удалённой точке плоскости a,b;
2) при D=0 числители выражений (6.15) также обращаются в нули; в этом случае получается соотношение
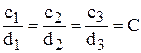
т.е. уравнения (6.15) отличаются друг от друга только постоянным множителем С, и одно уравнение является следствием другого. В этом случае для a и b получается бесконечная совокупность точек, лежащих на одной прямой:
Эта прямая, называется особой, она может пересекать границу области устойчивости или проходить через её начало. Точки особой прямой называются исключительными и в большинстве случаев соответствуют значениям w=0 и w=Ґ. Особая прямая, соответствующая обращению корня в нуль, определяется из условия равенства нулю свободного члена характеристического уравнения, а соответствующая обращению в бесконечность – при приравнивании к нулю коэффициента при старшей степени характеристического уравнения.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет