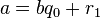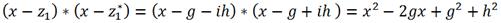что такое кратность корня многочлена
Понятие множественности важно для правильного подсчета без указания исключений (например, двойные корни считаются дважды). Отсюда и выражение «считать по множественности».
Если игнорировать множественность, это можно подчеркнуть, подсчитав количество различных элементов, например, «количество различных корней». Однако всякий раз, когда формируется набор (в отличие от мультимножества), множественность автоматически игнорируется, без необходимости использования термина «отдельный».
СОДЕРЖАНИЕ
Кратность простого множителя
кратность простого множителя 2 равна 2, в то время как кратность каждого из простых множителей 3 и 5 равна 1. Таким образом, число 60 имеет четыре простых множителя, учитывающих кратности, но только три различных простых множителя.
Кратность корня многочлена
Поведение полиномиальной функции вблизи кратного корня
График из полиномиальной функции F коснется й ось й на действительных корнях многочлена. График касается его в кратных корнях f и не касается простых корней. Граф пересекает ось x в корнях нечетной кратности и не пересекает ее в корнях четной кратности.
Кратность пересечения
Это определение позволяет нам точно сформулировать теорему Безу и ее обобщения.
В комплексном анализе
Кратный корень
Смотреть что такое «Кратный корень» в других словарях:
КРАТНЫЙ КОРЕНЬ алгебраического — уравнения такое число b, что f(х) делится без остатка на 2 ю или более высокую степень m двучлена (х b); число m кратность корня b … Большой Энциклопедический словарь
Основная теорема алгебры — утверждает, что Всякий отличный от константы многочлен (от одной переменной) с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел. Эквивалентная формулировка теоремы следующая: Поле комплексных чисел… … Википедия
Штурма правило — правило, позволяющее находить непересекающиеся интервалы, содержащие каждый по одному действительному корню данного алгебраического многочлена с действительными коэффициентами. Дано в 1829 Ж. Ш. Ф. Штурмом. Для любого многочлена f(x) без… … Большая советская энциклопедия
КОНЕЧНЫХ РАЗНОСТЕЙ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются функции при дискретном изменении аргумента, в отличие от дифференциального и интегрального исчислений, где аргумент изменяется непрерывно. Пусть функция y=f(x)задана в точках xk=x0+kh(h постоянная, к целое).… … Математическая энциклопедия
ЭЛЛИПТИЧЕСКАЯ КРИВАЯ — неособая полная алгебраическая кривая рода 1. Теория Э. к. является истоком большей части современной алгебраич. геометрии. Но исторически теория Э. к. возникла как часть анализа, как теория эллиптических интегралов и эллиптических функций.… … Математическая энциклопедия
КАТАСТРОФ ТЕОРИЯ — совокупность приложений теории особенностей дифференцируемых (гладких) отображений X. Уитни (Н. Whitney) и теории бифуркаций А. Пуанкаре (Н. Poincare) и А. А. Андронова. Назв. введено Р. Томом (R. Thorn) в 1972. К. т. применяется к геом. и физ.… … Физическая энциклопедия
КВАДРАТНОЕ УРАВНЕНИЕ — алгебраическое уравнение 2 й степени. Общий вид К. у. В поле комплексных чисел К. у. имеет два решения, выражающиеся в радикалах через коэффициенты этого уравнения: При b2>4ас оба решения К. у. действительные и различные, при b2 Математическая энциклопедия
Понятие множественности важно для правильного подсчета без указания исключений (например, двойные корни считается дважды). Отсюда и выражение «считать по множественности».
Если игнорировать множественность, это можно подчеркнуть, подсчитав количество отчетливый элементы, например, «количество различных корней». Однако всякий раз, когда формируется набор (в отличие от мультимножества), множественность автоматически игнорируется, не требуя использования термина «отдельный».
Содержание
Кратность простого множителя
кратность простого множителя 2 равна 2, а кратность каждого из простых множителей 3 и 5 равна 1. Таким образом, число 60 имеет четыре простых множителя, учитывающих кратности, но только три различных простых множителя.
Кратность корня многочлена
Поведение полиномиальной функции вблизи кратного корня
Кратность пересечения
В алгебраическая геометрия, пересечение двух подмногообразий алгебраического многообразия есть конечное объединение неприводимые разновидности. К каждому компоненту такого пересечения прикрепляется кратность пересечения. Это понятие местный в том смысле, что его можно определить, глядя на то, что происходит в окрестностях любого общая точка этого компонента. Отсюда следует, что без ограничения общности мы можем рассматривать, чтобы определить кратность пересечения, пересечение двух родственные сорта (подмногообразия аффинного пространства).
Это определение позволяет нам утверждать Теорема Безу и его обобщения точно.
Это определение кратности пересечения, которое по существу связано с Жан-Пьер Серр в его книге Локальная алгебра, работает только для теоретико-множественных компонентов (также называемых изолированные компоненты) перекрестка, а не для встроенные компоненты. Были разработаны теории для работы со встроенным корпусом (см. Теория пересечения подробнее).
В комплексном анализе
Понятие множественности важно для правильного подсчета без указания исключений (например, двойные корни считается дважды). Отсюда и выражение «считать по множественности».
Если игнорировать множественность, это можно подчеркнуть, подсчитав количество отчетливый элементы, например, «количество различных корней». Однако всякий раз, когда формируется набор (в отличие от мультимножества), множественность автоматически игнорируется, не требуя использования термина «отдельный».
Содержание
Кратность простого множителя
кратность простого множителя 2 равна 2, а кратность каждого из простых множителей 3 и 5 равна 1. Таким образом, число 60 имеет четыре простых множителя, учитывающих кратности, но только три различных простых множителя.
Кратность корня многочлена
Поведение полиномиальной функции вблизи кратного корня
Кратность пересечения
В алгебраическая геометрия, пересечение двух подмногообразий алгебраического многообразия есть конечное объединение неприводимые разновидности. К каждому компоненту такого пересечения прикрепляется кратность пересечения. Это понятие местный в том смысле, что его можно определить, глядя на то, что происходит в окрестностях любого общая точка этого компонента. Отсюда следует, что без ограничения общности мы можем рассматривать, чтобы определить кратность пересечения, пересечение двух родственные сорта (подмногообразия аффинного пространства).
Это определение позволяет нам утверждать Теорема Безу и его обобщения точно.
Это определение кратности пересечения, которое по существу связано с Жан-Пьер Серр в его книге Локальная алгебра, работает только для теоретико-множественных компонентов (также называемых изолированные компоненты) перекрестка, а не для встроенные компоненты. Были разработаны теории для работы со встроенным корпусом (см. Теория пересечения подробнее).
В комплексном анализе
Разложение полинома на множители. Кратные корни. Теорема о необходимом и достаточном условии существовании кратного корня
Любой многочлен степени n вида 
представляется произведением постоянного множителя при старшей степени 
и n линейных множителей 
, i=1, 2, …, n, то есть 
, причем 
, i=1, 2, …, n являются корнями многочлена.
Эта теорема сформулирована для комплексных корней , i=1, 2, …, n и комплексных коэффициентов 
, k=0, 1, 2, …, n. Она является основой для разложения любого многочлена на множители.
Если коэффициенты , k=0, 1, 2, …, n – действительные числа, то комплексные корни многочлена ОБЯЗАТЕЛЬНО будут встречаться комплексно сопряженными парами.
К примеру, если корни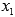 
и 
многочлена являются комплексно сопряженными, а остальные корни действительные, то многочлен представится в виде 
, где 
Замечание.
Среди корней многочлена могут быть повторяющиеся.
Доказательство теоремы проводится с использованием основной теоремы алгебры и следствия из теоремы Безу.
Определение. Число 
называется корнем полинома 
, если 
.
В силу теоремы Безу это равносильно тому, что 
.
Определение. Число называется корнем кратности 
полинома , если 
и 
. Корни кратности 1 называются простыми корнями, корни кратности больше 1 называются кратными корнями.
Теорема. Если — корень кратности полинома , то — корень кратности 
полинома 
. Если — общий корень 
, то — кратный корень .
Доказательство. Пусть — корень кратности полинома .
1. Если 
, то — корень кратности многочлена .
2. Если корень , то и, значит, — кратный корень многочлена .
Наибольший общий делитель. Алгоритм Евклида
Общим делителем нескольких чисел называется число, которое является делите-лем каждого из них. Например, числа 36, 60, 42 имеют общие делители 2, 3 и 6. Среди всех общих делителей всегда есть наибольший, в данном случае это 6. Это и есть наибольший общий делитель (НОД).
Чтобы найти наибольший общий делитель (НОД) нескольких чисел надо:
1) представить каждое число как произведение его простых множителей, например:
2) записать степени всех простых множителей:
3) выписать все общие делители (множители) этих чисел;
4) выбрать наименьшую степень каждого из них, встретившуюся во всех произведениях;
5) перемножить эти степени.
Алгоритм Евклида для целых чисел
Пусть 
и 
— целые числа, не равные одновременно нулю, и последовательность чисел
определена тем, что каждое 
— это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть
Тогда НОД(a,b), наибольший общий делитель и , равен 
, последнему ненулевому члену этой последовательности.
Существование таких 
, то есть возможность деления с остатком 
на 
для любого целого и целого 
, доказывается индукцией по m.
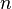
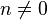
Корректность этого алгоритма вытекает из следующих двух утверждений:
Пусть 
, тогда НОД (a, b) = НОД (b, r).
Операция освобождения полинома от кратных корней
Вещественные полиномы. Разложение полинома на множители первой и второй степени.
Как известно, если комплексное число 
– корень многочлена, то обязательно и комплексно сопряженное ему число 
является корнем многочлена. Поэтому их произведение
представляет собой квадратичное выражение.
Таким образом, любой многочлен с действительными коэффициентами всегда можно представить в виде произведения линейных и квадратичных множителей
Подбор корней многочлена.
В общем случае найти корни многочлена степени n довольно сложная задача, но можно попытаться найти хотя бы один корень x0. Разделив исходный многочлен на одночлен x-x0, мы получим многочлен степени n-1. Тем самым мы упростили исходную задачу, так как раскладывать на множители теперь надо многочлен степени n-1. Например, для многочлена третьей степени после деления на x0 мы получим многочлен второй степени, корни которого найдем, просто решив квадратное уравнение. Существенную помощь в подборе рациональных корней многочлена может оказать следующая теорема.
(причем эта дробь несократима), то p – делитель свободного члена a0, а q – делитель старшего коэффициента an. Из этой теоремы следует, что если старший коэффициент равен единице, то целые корни многочлена следует искать только среди делителей свободного члена.