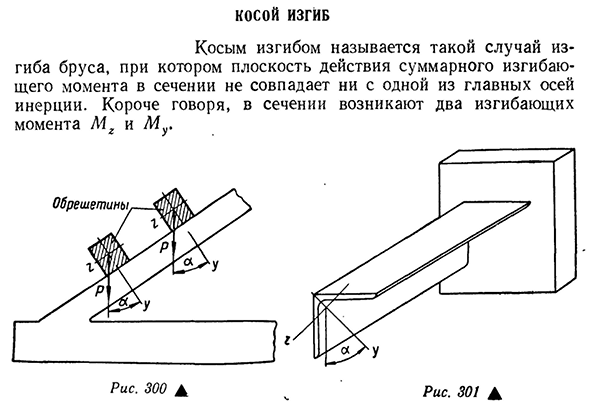
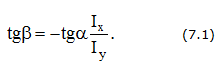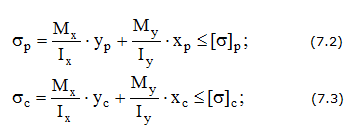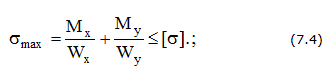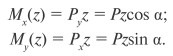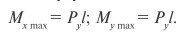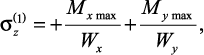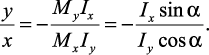что такое косой изгиб
iSopromat.ru
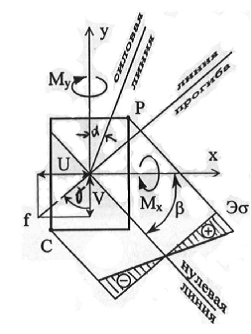
Косой изгиб — разновидность сложного сопротивления, при которой плоскость действия результирующего изгибающего момента не совпадает ни с одной из плоскостей симметрии поперечного сечения (рис. 7.1).
Угол наклона нейтральной линии
Условия прочности
— для сечения балки произвольной формы
здесь Mx, My — изгибающие моменты соответственно в вертикальной и горизонтальной плоскостях,
[σ] — допустимые напряжения.
— для сечений типа прямоугольник, двутавр и швеллер
где Wx, Wy — осевые моменты сопротивления сечения балки.
Перемещения и расчет на жесткость
Полный прогиб f балки в рассматриваемом сечении
v и u — прогибы балки в вертикальном и горизонтальном направлениях.
При плоском косом изгибе линия результирующего прогиба перпендикулярна к нейтральной линии.
[f] — допустимый прогиб.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Косой (двойной) изгиб
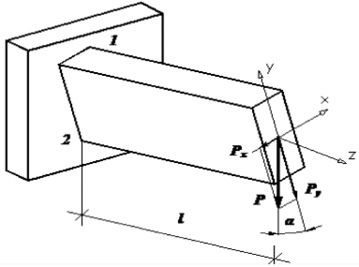
Такой случай имеет место, например, при изгибе консольного бруса силой, приложенной к плоскости торцового сечения под некоторым углом α к его оси симметрии (рис. 10.1). Косой изгиб является плоским, то есть изогнутая ось балки остается после деформации плоской кривой, но характеризуется тем, что в отличие от прямого изгиба, силовая плоскость и плоскость, в которой расположена изогнутая ось (плоскость изгиба), не совпадают.
Проведем сечение на расстоянии x (рис. 10.1) от правого конца бруса и рассмотрим равновесие отсеченной правой его части.

На основании принципа независимости действия сил косой изгиб рассматривается как результат действия на брус двух прямых изгибов, действующих в главных плоскостях. Этот принцип применим, если напряжения от отдельного действия изгибающих моментов, а также суммарное напряжение, не превышают предела пропорциональности. Нормальное напряжение σ в какой-либо точке поперечного сечения при косом изгибе получим как алгебраическую сумму нормальных напряжений, вызванных в той же точке моментами M y и M z :


После преобразований получаем:

где угловой коэффициент уравнения нейтральной линии равен

Таким образом, нейтральная линия при косом изгибе всегда проходит через центр тяжести сечения.
Для сечений, имеющих оси симметрии и выступающие углы (см. рис. 10.2), опасными будут угловые точки, в которых напряжения от обоих изгибающих моментов имеют одинаковый знак.
Напряжения в опасных точках определяются по формуле (10.1) путем подстановки в нее координат этих точек. Условие прочности при косом изгибе запишется так:

Из формулы (10.3) следует, что нейтральная линия наклонена к оси z под углом β :

В то же время тангенс угла наклона вектора 

Таким образом, в общем случае между углами α и β существует следующее соотношение:

Полное перемещение δ центра сечения бруса, как следует из принципа независимости действия сил и представления косого изгиба в виде комбинации двух плоских изгибов, равно геометрической сумме перемещений, вызванных каждым из указанных плоских изгибов в отдельности (см. рис. 10.2), то есть:

Перемещения δ y и δ z в главных плоскостях определяются способом Мора или другими, рассмотренными выше методами. При этом в общем случае справедливы следующие равенства:


где функция f ( x ) определяется условиями нагружения и закрепления концов бруса. Угол наклона вектора полного перемещения по отношению к оси y :

При косом изгибе прямого бруса нагрузками, расположенными в одной плоскости, упругая линия бруса будет плоской кривой. Однако плоскость изгиба не совпадает с плоскостью действия нагрузки.
Если внешние силы и пары, изгибающие брус, будут располагаться в разных плоскостях, то изогнутая ось бруса будет пространственной кривой.
Косой изгиб и изгиб балки








Косой изгиб
Чистый вес углов, скрепленных одним концом со стеной(рис. 301) вызывает косой изгиб, так как основная ось углового сечения наклонена к грузу под определенным углом. Рассмотрим отдельно ряд наиболее важных вопросов, связанных с расчетом стержня косого изгиба. 1. Определение давления при косом изгибе Рассмотрим балку, герметизированную на одном конце, на которую воздействует сила Р, приложенная к центру тяжести концевого участка под углом а к оси ОУ(рис. 302). Тонны 1 2 Икс п Рис 302D Раскладываем силу Р вдоль осей координат на две составляющие: Р У=Р Соса;Р РГ-R51pa.
(Слизь) Изгибающий момент сечения TP для инерциальной главной оси в соответствии с установленными правилами знака определяется Людмила Фирмаль
уравнением: Mg—RUX= — RH co8a; Mi= — R; x-RH81p a. (11.2) Поэтому в каждом сечении стержня действуют одновременно два изгибающих момента, приводящих к изгибу в двух основных плоскостях. Чтобы определить напряжение от каждого момента отдельно, используйте ранее полученную формулу для плоского изгиба. Используя принцип независимости сил, мы можем- Нет необходимости писать общую формулу напряжения в любой точке положительной четверти 349 координатных осей, Миллиграмм 2. И= (11.3) По формуле (11.3)можно определить напряжение в любой точке сечения. Вместо этого
принадлежащих одновременно волокнам, наиболее удаленным от основной оси инерции section.applied.In чаще всего поперечное сечение не имеет таких точек и в то же время является наиболее удаленным от обеих осей. Например, о разделе, показанном на рисунке. Например, Точка 2 находится дальше от оси Og, чем другие точки, А Точка 2 ближе к оси OU, чем точка 3. Рис 303а Рис 304D Например, для Seche-304, Дост- Максимальные условия напряжения используются в Формуле (11.3). В таких случаях сначала находят точку, в которой напряжение максимально. Часто эта задача решается путем расчета напряжений в нескольких точках.
Поэтому NII показан на рисунке. Вот именно!. Рассчитайте напряжение в трех точках-1, 2 и 3, и установите максимальное значение. В любом сечении нужно Людмила Фирмаль
сначала установить положение нулевой линии, а затем наиболее удаленные точки от остальных. Легко показать, что в это время напряжение будет максимальным. Фактически равенство (11.3) является уравнением плоскости, проходящей через нулевую линию. Расстояние, измеренное поперечным сечением до этой плоскости, численно равно напряжению в этой точке. Это будет максимум для самых удаленных точек от нулевой линии. Из нормального от креста 3512 определение положения нулевой линии в поперечном сечении балки при косом изгибе Положение нулевой линии при косом изгибе можно установить путем выравнивания напряжения в точке,
принадлежащей этой линии, до нуля. Предположим, что текущие координаты нулевой линии равны yy и g^, а затем применяем формулу (11.3) к、 Иметь N+ Где его найти Уй Му у мг (П. Пять) Правая часть уравнения (11.5) положительна, если оси выбраны так, что моменты m y и M2 имеют одинаковый знак. В этом случае знак y и y при заполнении формулы (11.5)!y и g/> / различны. Поэтому «нулевая линия» не может пройти через первую четверть(рис. 305, а). Учитывая, что через Og O2=517-700= — 183кг / см2;A3^ _ _517 4-700=183кг/см2;O4= — 517-700= — 1217кг / см2. Двенадцать. 355 согласно этим данным строится диаграмма напряжений для участка в
уплотнении, которая показана на рисунке. Это указывает на напряжение в самой дальней точке полки и средней линии стены. Найдите положение нулевой линии в уплотнении. Подставим значение изгибающего момента в Формулу (11.6) и учтем его=2550pch4;
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Научная электронная библиотека
Лекция 14. СЛОЖНОЕ СОПРОТИВЛЕНИЕ
Понятие о сложном сопротивлении, его виды. Изгиб с растяжением. Косой изгиб.
Cложное сопротивление – такие виды нагружения бруса, при которых в поперечных сечениях возникают одновременно не менее двух внутренних силовых факторов.
Случаи сложного сопротивления условно разделяют на два вида. Первый вид составляют случаи сложного сопротивления, при которых в опасных точках бруса напряженное состояние является одноосным. В эту группу объединяют: изгиб с растяжением, косой изгиб, внецентренное растяжение-сжатие и др.
Рис. 41. Изгиб с растяжением
Условие прочности при изгибе с растяжением, пренебрегая действием поперечных сил, имеет вид:
Ко второй группе относятся такие случаи сложного сопротивления, когда напряженное состояние является плоским. Например, изгиб с кручением, растяжение(сжатие) с кручением и т.д. Для случая нагружения, относящегося к первой группе, в отличие от второй группы, нет необходимости в применении гипотез прочности.
Косой изгиб проявляется, если прикладываем к балке вертикальную нагрузку, и она при этом изгибается не только в вертикальной плоскости, но и вбок. Косой изгиб – это изгиб, при котором изогнутая ось стержня не лежит в силовой плоскости. Косой изгиб невозможен для балок с сечениями, у которых все центральные оси являются главными (например, квадрат, круг).
Рассмотрим консольную балку прямоугольного сечения длиной l, нагруженную вертикальной силой P. Главная центральная ось балки (ось симметрии) y составляет некоторый малый угол α с направлением действия нагрузки.
Рис. 42. Косой изгиб
Оба изгибающих момента будут наибольшими в жесткой заделке:
Формула суммарных нормальных напряжений при косом изгибе в произвольном поперечном сечении балки для некоторой точки с координатами x и y:
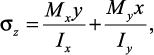
где 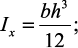
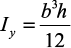
Наибольшие нормальные напряжения при косом изгибе возникнут в поперечном сечении, расположенном в жесткой заделке, в наиболее удаленных от соответствующих нейтральных осей точках 1 и 2: y = h/2, x = b/2. В точке 1 напряжения будут растягивающими:
а в точке 2 – такими же по величине, но сжимающими.
В формулах максимальных нормальных напряжений при косом изгибе 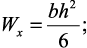
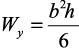
Нейтральная линия – это геометрическое место точек поперечного сечения стержня, в которых нормальные напряжения равны нулю.
Из определения нейтральной линии легко находится положение нейтральной линии, приравнивая правую часть выражения 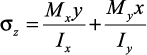
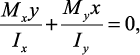
При косом изгибе условие прочности имеет вид:
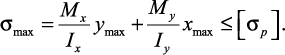
Косой изгиб опасен тем, что при производственном браке (перекосе) могут существенно увеличиться нормальные напряжения в балке.
Лекция № 14
Сложное сопротивление. Косой изгиб. Определение внутренних усилий, напряжений, положения нейтральной оси при чистом косом изгибе. Деформации при косом изгибе.
14. СЛОЖНОЕ СОПРОТИВЛЕНИЕ. КОСОЙ ИЗГИБ
Рассмотренные нами до сих пор случаи нагружения элементов конструкций (растяжение-сжатие, сдвиг, кручение, плоский изгиб) относят сопротивление стержня к одному (п р о с т о м у) виду деформации. С л о ж н ы м соответствует два и более простых видов.
Сложное сопротивление – вид нагружения, представляющий собой комбинацию (сочетание) нескольких простых типов сопротивления.
В случае сложного сопротивления в поперечных сечениях элемента возникает два и более внутренних усилия. При этом расчет элементов при сложном сопротивлении ведется в рамках принципа независимости действия сил. То есть, каждый из простых видов сопротивления, входящих в состав сложного, рассматривается независимо от остальных, а затем находится суперпозиция (сумма) полученных решений (для внутренних усилий, напряжений, деформаций и т. д.). Принцип суперпозиции применим только для линейно-упругих систем.
14.1. Общие понятия о косом изгибе
с одной из главных плоскостей инерции балки. Однако существуют и более общие случаи изгиба, когда силы действуют в плоскости, не совпадающей с
плоскостью инерции (к о с о й изгиб), или, вообще, силы не лежат в одной плоскости (с л о ж н ы й или неплоский изгиб).
Косой изгиб – изгиб, при котором плоскость P действия изгибающих моментов и поперечных сил не совпадает ни с одной из главных плоскостей инерции бруса.
14.2. Определение внутренних усилий при косом изгибе
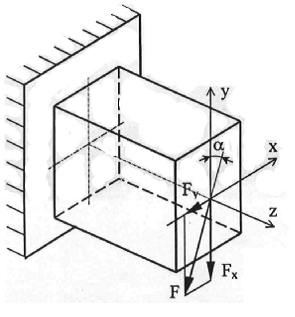
определяя внутренние усилия при косом изгибе консольной балки под дейст-
вием сосредоточенной силы F на свободном конце (см. рисунок):
∑ F y = 0 Q y = F cos α ;
∑ M y = 0 M y = F sin α x ;
∑ F z = 0 Q z = F sin α ;
Аналогичные усилия возникают и в более общем случае сложного (неплоского) изгиба.
Правило знаков для внутренних усилий: изгибающие моменты – положи-
тельны, если вызывают растяжение в положительном квадранте координатной системы zOy ; поперечные силы – положительны, если под их действием отсеченный элемент поворачивается по часовой стрелке.
Таким образом, косой изгиб может быть представлен как совместное действие двух плоских изгибов в двух взаимно перпендикулярных плоскостях инерции.