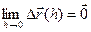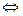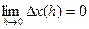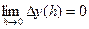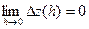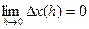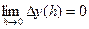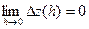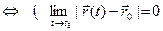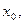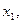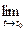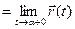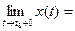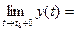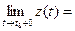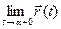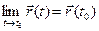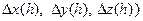что такое координатная функция

Что такое Функция?

7 класс, 11 класс, ЕГЭ/ОГЭ

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Источник

Вектор-функции

Предел и непрерывность вектор-функции.

Понятие вектор-функции.

Если каждому значению \(t\in E\), где \(E\subset\mathbb\), поставлен в соответствие вектор \(r(t)\) трехмерного пространства, то говорят, что на множестве \(E\) задана векторная функция \(r(t)\) скалярного аргумента \(t\).

Пусть в пространстве фиксирована прямоугольная система координат \(Oxyz\). Тогда задание вектор-функции \(r(t),\ t\in E\), означает задание координат \(x(t),\ y(t),\ z(t)\) вектора \(r(t),\ t\in E\). Если \(i,j,k\) — единичные векторы координатных осей, то
$$
r(t)=x(t)i+y(t)j+z(t)k,\qquad t\in E,\nonumber
$$
или
$$
r(t)=(x(t),y(t),z(t)).\nonumber
$$
Если \(z(t)=0\) при всех \(t\in E\), то вектор-функцию \(r(t)\) называют двумерной.

В случае, когда начало каждого из векторов \(r(t)\) совпадает с началом координат (рис. 21.1), эти векторы называют радиус-векторами, а множество их концов — годографом вектор-функции \(r(t)\), \(t\in E\), который можно рассматривать как траекторию точки \(M(t)\) конца вектора \(r(t)\), если считать, что \(t\) — время.

Предел вектор-функции.

Вектор \(a\) называют пределом вектор-функции \(r(t)\) в точке \(t_0\) и пишут \(\displaystyle \lim_>r(t)=a\) или \(r(t)\rightarrow a\) при \(t\rightarrow t_0\), если
$$
\lim_> |r(t)-a|=0,\label
$$
то есть длина вектора \(r(t)-a\) стремится к нулю при \(t\rightarrow t_0\).

Рис. 20.1

Если заданы \(r(t)=(x(t),y(t),z(t))\) и \(a=(a_<1>,a_<2>,a_<3>)\), то
$$
\lim_>r(t)=a\label
$$
тогда и только тогда, когда
$$
x(t)\rightarrow a_1,\ y(t)\rightarrow a_2,\ z(t)\rightarrow a_3\quad при \ t\rightarrow t_0.\label
$$

Поэтому, если \(r(t)\rightarrow a\) при \(t\rightarrow t_0\), то есть выполняется условие \eqref, то выполняется условие \eqref.

Обратно: если выполняются условия \eqref, то из равенства \eqref следует, что выполнено условие \eqref. \(\bullet\)

При доказательстве свойств предела вектор-функции удобно использовать следующее очевидное утверждение: условие \eqref выполняется в том и только том случае, когда
$$
r(t)=a+\alpha(t),\nonumber
$$
где \(\alpha(t)\) — бесконечно малая вектор-функция, то есть
$$
\alpha(t)\rightarrow 0\quad \mbox <при>\ t\rightarrow t_<0>.\nonumber
$$

Свойства пределов вектор-функций.

\(\circ\) Это свойство следует из неравенства
$$
||r(t)|-|a|| \leq |r(t)-a|.\qquad \bullet\nonumber
$$

Если \(r(t)\rightarrow a\) при \(t\rightarrow t_<0>\), а скалярная функция \(f(t)\) такова, что \(f(t)\rightarrow A\) при \(t\rightarrow t_<0>\), то \(f(t)r(t)\rightarrow Aa\) при \(t\rightarrow t_<0>\), то есть
$$
\lim_f(t)r(t)=\lim_>f(t)\lim_r(t).\label
$$

\(\circ\) Из определений пределов скалярной функции и вектор-функции следует, что \(r(t)=a+\alpha(t),\ f(t)=A+\beta(t)\), где \(\alpha(t)\) — бесконечно малая вектор-функция, \(\beta(t)\) — бесконечно малая функция при \(t\rightarrow t_0\). Поэтому \(f(t)r(t)=Aa+\gamma(t)\), где \(\gamma(t)=A\alpha(t)+\beta(t)a+\beta(t)\alpha(t)\) — бесконечно малая вектор-функция при \(t\rightarrow t_0\), откуда получаем равенство \eqref. \(\bullet\)

\(\circ\) По условию \(r_(t)=a_+\alpha_\), где \(a_i(t)\rightarrow 0\) при \(t\rightarrow t_<0>\ (i=1,2)\). Поэтому \(r_1(t)+r_2(t)=a_1+a_2+\beta(t)\), где \(\beta(t)=\alpha_<1>(t)+\alpha_2(t)\rightarrow 0\) при \(t\rightarrow t_<0>\), откуда следует \eqref. Докажем формулу \eqref. В силу свойств скалярного произведения
$$
(r_<1>(t),r_2(t))-(a_1,a_2)=(\alpha_<1>(t),a_<2>)+(\alpha_<2>(t),a_1)+(\alpha_1(t),\alpha_2(t)),\nonumber
$$
причем в правой части этого равенства — бесконечно малая функция, так как \(\alpha_<1>(t),\alpha_<2>(t)\) — бесконечно малые вектор-функции и \(|(p,q)| \leq |p|\cdot|q|\) для любых векторов \(p\) и \(q\).

Аналогично доказывается формула \eqref, в этом случае следует воспользоваться неравенством \(|[p,q]| \leq |p|\cdot|q|\). \(\bullet\)

Непрерывность вектор-функции.

Вектор-функцию \(r(t)\) называют непрерывной при \(t=t_<0>\), если
$$
\lim_>r(t)=r(t_0).\label
$$
Непрерывность вектор-функции \(r(t)=(x(t),y(t),z(t))\) при \(t=t_<0>\) в силу эквивалентности условий \eqref и \eqref означает, что ее координаты \(x(t),y(t),z(t)\) непрерывны в точке \(t_<0>\).

Назовем вектор-функцию \(\Delta r=r((t_0+\Delta t)-r(t_0)\) приращением вектор-функции \(r(t)\) в точке \(t_<0>\). Тогда условие \eqref означает, что
$$
\Delta r\rightarrow 0\quad при\quad \Delta t\rightarrow 0.\label
$$

Из определения непрерывности вектор-функции и свойств пределов векторных функций следует, что сумма, векторное и скалярное произведения вектор-функций \(r_1(t)\) и \(r_2(t)\) являются непрерывными функциями при \(t=t_<0>\), если вектор-функции \(r_1(t)\) и \(r_2(t)\) непрерывны в точке \(t_<0>\).

Производная и дифференциал вектор-функции.

Производная вектор-функции.

Если существует \(\displaystyle \lim_<\Delta t\rightarrow 0>\frac<\Delta r><\Delta t>\) где \(\Delta r=r(t_0+\Delta t)-r(t_0)\), то этот предел называют производной вектор-функции \(r(t)\) в точке \(t_0\) и обозначают \(r'(t_0)\) или \(\dot(t_0)\).

Таким образом,
$$
r'(t_<0>)=\lim_<\Delta t\rightarrow 0>\frac+\Delta t)-r(t_<0>)><\Delta t>.\label
$$
Аналогично вводится понятие второй производной
$$
r″(t_<0>)=\lim_<\Delta t\rightarrow 0>\frac+\Delta t)-r'(t_<0>)><\Delta t>\nonumber
$$
и производной порядка \(n > 2\) вектор-функции. Заметим, что если \(r(t)=(x(t),y(t),z(t))\), то
$$
r'(t_<0>)=(x'(t_0),y'(t_0),z'(t_0))\label
$$
Утверждение \eqref следует из определения \eqref и свойств пределов вектор-функций.

Аналогично, если существует \(r″(t_<0>)\), то
$$
r″(t_<0>)=(x″(t_0),y″(t_0),z″(t_0)).\nonumber
$$
Из определения производной следует, что \(\Delta r=r'(t_0)\Delta t+\alpha(\Delta t)\Delta t\), где \(\alpha(\Delta t)\rightarrow 0\) при \(\Delta t\rightarrow 0\), и потому \(\Delta r\rightarrow 0\) при \(\Delta t\rightarrow 0\). Таким образом, выполняется условие \eqref, то есть вектор-функция \(r(t)\), имеющая производную в точке \(t_<0>\), непрерывна при \(t=t_<0>\).

\(\circ\) Формулы \eqref-\eqref справедливы в точке \(t\), если в этой точке соответствующие функции имеют производные. Ограничимся доказательством формулы \eqref. Пусть \(\Delta r_\) — приращение вектор-функции \(r_k(t)\), соответствующее приращению аргумента \(\Delta t\), то есть \(\Delta r_k=r_k(t+\Delta t)-r_k(t),\ k=1,2\). Тогда, используя свойства скалярного произведения и свойства пределов вектор-функций, получаем
$$
\begin
(r_<1>,r_<2>)’=\displaystyle\lim_<\Delta t\rightarrow 0>\frac<(r_<1>(t+\Delta t),r_<2>(t+\Delta t))-(r_<1>(t),r_<2>(t))><\Delta t>=\\
=\lim_<\Delta t\rightarrow 0>\left[\left(r_<1>(t),\frac<\Delta r_<2>(t)><\Delta t>\right)+\left(\frac<\Delta r_<1>(t)><\Delta t>,r_2(t)\right)+\left(\frac<\Delta r_<1>(t)><\Delta t>,\Delta r_2(t)\right)\right]=\\
=(r_1,r_2′)+(r_1′,r_2),
\end\nonumber
$$
так как \(\displaystyle \frac<\triangle \mathrm_><\triangle t>\rightarrow r_‘(t)\) при \(\Delta t\rightarrow 0\ (i=1,2)\) и \(\Delta r_2\rightarrow 0\) при \(\Delta t\rightarrow 0\). \(\bullet\)

Пусть существует \(r'(t)\) для всех \(t\in(\alpha,\beta)\) и пусть \(|r(t)|=C=const\) для всех \(t\in(\alpha,\beta)\).

Доказать, что \((r(t),r'(t))=0\), то есть векторы \(r(t)\) и \(r'(t)\) ортогональны.

\(\triangle\) Используя формулу \(|r(t)|^2=(r(t),r(t))\), правило дифференцирования скалярного произведения (формула \eqref) и условие \(|r(t)|=C\), получаем \((r(t),r(t))’=2(r'(t),r(t))=0\), так как \(|r(t)|^<2>)’=(C^<2>)’=0\). Итак,
$$
|r(t)|=C\Rightarrow (r(t),r'(t))=0.\quad\blacktriangle\nonumber
$$

Дифференциал вектор-функции.

Вектор-функцию \(r(t)\), определенную в некоторой окрестности точки \(t_<0>\), называют дифференцируемой при \(t=t_<0>\), если ее приращение \(\Delta r=r(t_<0>+\Delta t)-r(t_<0>)\) в точке \(t_<0>\) представляется в виде
$$
\Delta r=a\Delta t+\Delta t\alpha(\Delta t),\label
$$
где вектор \(a\) не зависит от \(\Delta t\), \(\alpha(\Delta t)\rightarrow 0\) при \(\Delta t\rightarrow 0\).

Полагая \(dt=\Delta t\), запишем равенство \eqref в виде
$$
dr=r’dt,\nonumber
$$
где опущено обозначение аргумента функции \(r’\). Отсюда получаем
$$
r’=\frac

.\label (21)
$$

Замена переменного.

Если функция \(t=t(s)\) дифференцируема при \(s=s_<0>,\ t(s_<0>)=t_<0>\), а вектор-функция \(r(t)\) дифференцируема в точке \(t_<0>\), то вектор-функция \(\rho(s)=r(t(s))\) дифференцируема в точке \(s_<0>\), а производная этой функции выражается формулой
$$
\rho’ (s_0)=r_s'(t(s_0))=r_‘(t_<0>)t_‘(s_<0>),\label
$$

где индекс указывает, по какому переменному производится дифференцирование.

\(\circ\) Функция \(\alpha(\Delta(t))\) в формуле \eqref не определена при \(\Delta t=0\). Доопределим ее при \(\Delta t=0\), полагая \(\alpha(0)=0\).

Так как \(t=t(s)\) — функция, дифференцируемая при \(s=s_0\), то \(\Delta t=t(s_<0>+\Delta s)-t(s_<0>)\rightarrow 0\) при \(\Delta s\rightarrow 0\). Разделив обе части равенства \eqref на \(\Delta s\neq 0\), получим
$$
\frac<\Delta r><\Delta s>=r'(t_0)\frac<\Delta t><\Delta s>+\alpha(\Delta t)\frac<\Delta t><\Delta s>.\label
$$
Правая часть \eqref имеет при \(\Delta s\rightarrow 0\) предел, равный \(r'(t_0)t'(s_0)\), так как \(\Delta t\rightarrow 0\) при \(\Delta s\rightarrow 0\) и \(\alpha(\Delta t)\rightarrow 0\) при \(\Delta t\rightarrow 0\). Следовательно, существует предел в левом части \eqref, и справедливо равенство \eqref. Формулу \eqref запишем кратко в виде равенства
$$
r_’=r_’t_’,\label
$$
выражающего правило дифференцирования вектор-функции при замене переменного. \(\bullet\)

Теорема Лагранжа и локальная формула Тейлора для вектор-функции.

Формула Лагранжа, то есть формула
$$
r(\beta)-r(\alpha)=r'(\xi)(\beta-\alpha),\quad \xi\in(\alpha,\beta),\label
$$
для вектор-функции, вообще говоря, неверна.

\(\circ\) В самом деле, пусть формула \eqref верна, и пусть \(r(t)=(\cos t,\sin t)\), тогда \(r'(t)=(-\sin t,\cos t),\ |r'(t)|=1\). Полагая \(\alpha=0,\beta=2\pi\), получим из равенства \eqref \(0=r(2\pi)-r(0)=r'(\xi)2\pi\), что невозможно, так как \(|r'(\xi)|=1\). \(\bullet\)

Если вектор-функция \(r(t)\) непрерывна на отрезке \([\alpha,\beta]\) и дифференцируема на интервале \((\alpha,\beta)\), то
$$
\exists\xi\in(\alpha,\beta):\ |r(\beta)-r(\alpha)|\leq|r'(\xi)|(\beta-\alpha).\label
$$

\(\circ\) Рассмотрим скалярную функцию
$$
\varphi(t)=(r(\beta)-r(\alpha),r(t)).\nonumber
$$
эта функция непрерывна на отрезке \([\alpha,\beta]\), так как вектор-функция \(r(t)\) непрерывна на этом отрезке. Кроме этого, функция \(\varphi(t)\) дифференцируема на интервале \((\alpha,\beta)\), так как функция \(r(t)\) дифференцируема этом интервале, причем в силу правила дифференцирования скалярного произведения
$$
\varphi'(t)=(r(\beta)-r(\alpha),r'(t)).\nonumber
$$
По теореме Лагранжа
$$
\exists\xi\in(\alpha,\beta):\ \varphi(\beta)-\varphi(\alpha)=\varphi'(\xi)(\beta-\alpha)\label
$$
Преобразуем левую часть неравенства \eqref:
$$
\begin
\varphi(\beta)-\varphi(\alpha)=(r(\beta)-r(\alpha),r(\beta))-(r(\beta)-r(\alpha),r(\alpha))=\\
=(r(\beta)-r(\alpha),r(\beta)-r(\alpha))=|r(\beta)-r(\alpha)|^2
\end\nonumber
$$
Тогда равенство \eqref примет вид
$$
|r(\beta)-r(\alpha)|^<2>=(r(\beta)-r(\alpha),r'(\xi))(\beta-\alpha).\label
$$
Если \(r(\beta)=r(\alpha)\), то неравенство \eqref справедливо при любом \(\xi\in \in(\alpha,\beta)\). Если \(r(\beta)\neq r(\alpha)\), то \(|r(\beta)-r(\alpha)| > 0\). Тогда, используя неравенство \(|(a,b)|\leq|a|\cdot|b|\), из формулы \eqref получим
$$
|r(\beta)-r(\alpha)|^<2>\leq|r(\beta)-r(\alpha)|\cdot |r'(\xi)|(\beta-\alpha),\nonumber
$$
откуда, разделив обе части неравенства на \(|r(\beta)-r(\alpha)| > 0\), получим неравенство \eqref. \(\bullet\)

Для вектор-функции \(r(t)\) справедлива локальная формула Тейлора
$$
r(t)=\sum_^\frac(t_<0>)>(t-t_<0>)^+\varepsilon(t-t_<0>),\label
$$
где \(\varepsilon(t-t_0)=o((t-t_<0>)^)\) — вектор-функция такая, что \(\varepsilon(t-t_0)=(t-t_<0>)^\varepsilon_<1>(t-t_<0>)\), где \(\varepsilon_<1>(t-t_<0>)\rightarrow 0\) при \(t\rightarrow t_<0>\).Эта формула справедлива в предположении, что существует \(r^<(n)>(t_0)\). Для доказательства формулы \eqref достаточно воспользоваться локальной формулой Тейлора для компонент вектор-функции \(r(t)\).

Источник

Вектор-функция, ее предел и непрерывность

Глава 3. ВЕКТОРНЫЕ ФУНКЦИИ

Контрольные вопросы

1.Что относится к государственной тайне?

2. Каков перечень сведений составляющих государственную тайну, отнесение сведений к государственной тайне?

3. Что представляет собой система защиты государственной тайны?

4. Какова процедура оформления права граждан на доступ к сведениям, составляющим государственную тайну?

5. Кто утверждает(ют) государственные программы в области защиты государственной тайны?

6. Что не подлежит к засекречиванию и отнесению к государственной тайне?

7. Кто обосновывает необходимость отнесения сведений к государственной тайне?

8. Что является основанием для рассекречивания сведений, составляющих государственную тайну?

9. Какие существуют степени секретности информации, отнесенной к государственной тайне?

10. Как осуществляется допуск должностных лиц и граждан РФ к государственной тайне?

11. Какие существуют формы допуска в соответствии со степенями секретности сведений, составляющих государственную тайну?

12. Для кого существует особый порядок допуска к сведениям, составляющим государственную тайну?

13. Каковы основания для отказа должностному лицу или гражданину в допуске к государственной тайне?

14. Кто организует исполнение закона «О государственной тайне»?

15. Кто осуществляет надзор за соблюдением закона «О государственной тайне»?

16. Кто осуществляет контроль обеспечения защиты государственной тайны.

17.Основные понятия, информационные ресурсы, пользование ими, информационные системы. Виды тайн в российском законодательстве.

Математическое понятие вектор-функции можно иллюстрировать разнообраз- ными примерами векторных величин, вэятыми из механики, физики и других естест- венных наук. Так, хаотичное броуновское движение малой частицы вызвано тем, что вектор действующей на неё силы (равнодействующей столкновений частицы с молеку- лами жидкости или газа) ежемоментно меняется и по направлению, и по величине. Эту силу можно рассматривать как вектор-функцию, аргументом которой является время.

В этом параграфе изложены основы дифференциального исчисления вектор-функций.

1.1. Основные понятия

= (x(t), y(t), z(t) ).

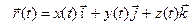
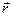
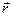
Функции x(t), y(t) и z(t) называют координатными функциями вектор-функции(t). Следовательно, если на множестве Т определена вектор-функция (t), то на Т определена и упорядоченная тройка (x(t), y(t), z(t) ) её координатных (скалярных) функ- ций.

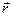
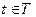
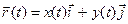
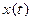
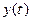
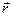
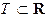
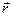
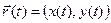
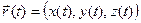
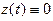
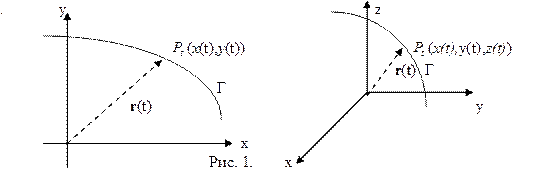
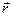
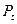
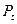
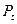
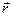
Может оказаться, что все значения (t), , компланарны, т.е. параллельны некоторой плоскости. Введя на этой плоскости декартову прямоугольную систему координат, получим: , где и – проекции вектора (t) на оси Ox и Oy соответственно. Таким образом, в этом случае задание на множестве T, , вектор- функции (t) эквивалентно заданию на T упорядоченной пары скаляр- ных функций:. Можно, конечно, и здесь считать, что на T задана упорядоченная тройка функций , причем на T. Везде ниже мы связываем задание вектор- функции с заданием упорядоченной тройки скалярных функций.

Удобной геометрической интерпретацией вектор- функции является её годограф.По- местим начало вектора (t) в начало координат и обозначим его конец через За- метим, что координатные функции образуют набор координат этой точки:(x(t), y(t), z(t)). Когда t, возрастая, пробегает множество T, точка перемещается, описывая некоторую кривую Г (см. рис. 1). Эту кривую и называют годографом вектор- функции (t). Переменную t называют параметром кривой Г, уравнения x = x(t), y = y(t), z = z(t) – параметрическими уравнениями кривой Г Систему

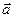
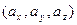
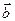
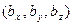
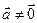
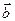
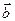
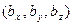
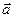
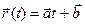
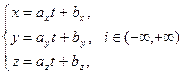
Пример 1. Пусть = и =, – заданные векторы. Отложим из начала координат O и обозначим через D прямую, проходящую через конец вектора , точку Впараллельно . При всяком вещественном t поло- жим: . Прямая D является годографом. этой вектор- функции, а система

— координатной формой уравнения прямой.

1.2. Предел вектор- функции в точке

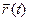
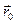
Пусть t₀ – вещественное число, а — вектор- функция определенная в проко- лотой окрестности Пусть, далее, — некоторый вектор.

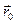
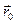
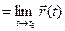
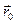
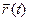
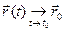
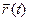
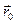
Если удовлетворяет условиям этого определения, будем записывать: = ( является пределом при t, стремящемся к t₀ ) или (стремится к при t, стремящемся к t₀ ).

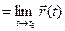
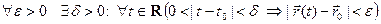
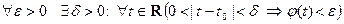
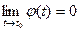
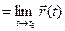
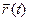
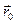
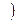
Итак, равенство по определению означает:

,

, т.е., ( см. определение предела скалярной функции на языке «ε-δ»). Таким образом, тогда и только тогда, когда длина разности — является бесконечно малой при tt₀ :

. (1)

Теорема 1 устанавливает связь между пределом вектор-функции и пределами её координатных функций

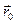
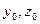
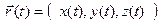
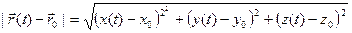
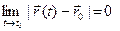
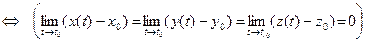
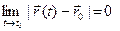
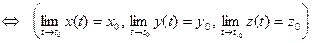
►Имеем: =() и . Отсюда:

. Подкоренное выражение представляет собой сумму трёх неотрицательных слагаемых; поэтому левая часть этого равенства стремится к нулю при тогда и только тогда, когда каждое из этих слагаемых стремится к нулю при , т.е.

( ) , что можно переписать так:

( ) (2) Утверждение теоремы следует из (1) и (2). ◄

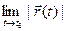
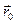
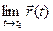
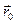
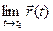
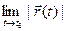
Замечание. Если =||, то вовсе не обязательно справедливо равенство =. Вместе с тем, справедливо утверждение:

= = 0

— это вытекает из (1) как частный случай при = .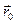

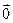
Опираясь на теорему о покоординатной сходимости можно доказывать теоремы о пределах вектор-функций, аналогичные теоремам о пределах скалярных функций.

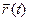
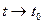
Теорема 2.(О единственности предела) Если вектор-функция имеет пре- дел при , то только один.

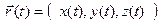
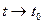
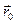
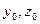
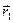
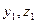
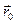
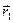
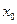
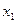
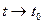
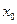
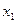
► Допустим, что вектор-функция имеет при при два различных предела: =() и =(). Так как ≠ , то упорядо- ченные тройки их координат не могут совпадать. Пусть, к примеру, ≠. В силу тео- ремы о покоординатной сходимости координатная функция x(t) должна при стремиться и к, и к; но это противоречит теореме о единственности предела ска- лярной функции. ◄

1) ; 2) ;

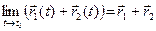
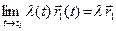
3) ; 4) .

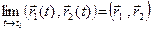
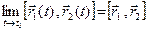
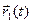
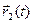
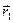
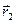
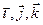
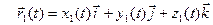
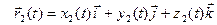
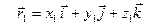
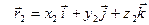
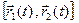
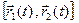
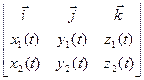
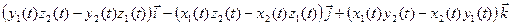
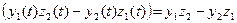
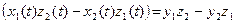
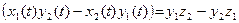
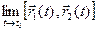
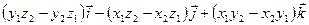
Запишем разложения векторов , , и по базису , составлено- му из ортов координатных осей:

, ,

, . Используя формулу векторной алгебры, запишем разложение вектора векторного про- изведения :

= =

= Из теоремы об арифметических действиях с пределами скалярных функций и теоремы о покоординатной сходимости следует:

;

;

. Опираясь на эти равенства и теорему о покоординатной сходимости, теперь получим:

= = . ◄

Замечание. Для векторов не определены отношения «больше» или «меньше»; утверждение « вектор больше вектора » смысла не имеет. По этой причине среди теорем о вектор-функциях нет аналогов тех теорем о пределах скалярных функций, формулировки которых содержат неравенства, а именно, теоремы о предельном пере- ходе в неравенстве, о стабилизации знака неравенства, о «сжатой» функции.

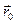
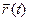
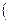
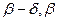
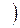
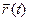
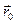
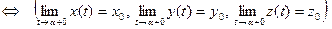
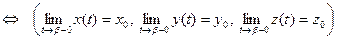
Определение. Вектор назовём односторонним пределом вектор-функции при t, стремящемся к α справа (при t, стремящемся к β слева ), если для любого ε> 0 можно указать δ>0 такое, что при всех t, принадлежащих интервалу (α, α + δ) при- надлежащих интервалу (), длина разности —меньше ε.

;

.

Теорема 4. (О связи предела вектор-функции с её односторонними пределами)

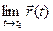
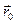
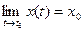
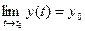
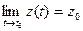
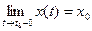
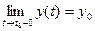
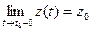
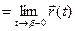
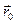
Необходимость. Пусть =. По теореме о покоординатной сходимости , , . Отсюда по теореме об односторонних пределах скалярной функции следует:, , .Отсюда и из сформулированных выше аналогов теоремы о покоординатной сходимости следует: =.

Доказывая Достаточность следует приведенные выше рассуждения располо- жить в обратном порядке. ◄

1.3. Непрерывность вектор- функции

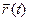
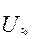
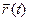
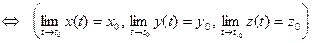
Теорема 5.(Критерий непрерывности) Пусть вектор-функция определена в окрестности . t₀. Для того, чтобы была непрерывной в точке t₀, необхо- димо и достаточно, чтобы каждая из её координатных функций была непрерывной в этой точке.

. Отсюда вытекает справедливость утверждений теоремы, так как равенство в левой части есть условие непрерывности вектор-функции в точке t₀, а равенства в правой части – условия непрерывности её координатных функций в той же точке. ◄

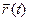
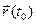
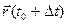
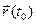
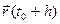
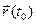
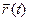
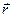
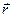
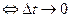
Разность t – t­₀ будем называть приращением аргумента t в точке t₀ и обозначать через Δt или h. Заметим: t = t­₀ + Δt= t­₀ + h. Вектор разности —= —= —назовем приращением вектор-функции в точке t₀ и обозначим че- рез Δили через Δ(h), подчеркнув во втором обозначении зависимость этого векто- ра от приращения h = Δt аргумента t. Заметим: .

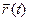
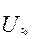
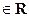
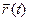
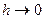
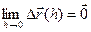
Теорема 6 (О приращении непрерывной вектор-функции) Пусть вектор-функция определена в окрестности . t₀. Для того, чтобы была непрерывной в точке t₀, необходимо и достаточно, чтобы её приращение было бесконечно малым при : .

= (

По теореме о покоординатной сходимости

( )(, , ). Отсюда и из теоремы 5 вытекает справедливость утверждений теоремы 6, так как по теореме о приращении непрерывной скалярной функции равенства , , представляют собой необходимые и достаточные условия непрерывности в точке t₀ соответствующих координатных функций ◄

Источник