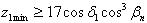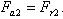что такое конусное расстояние
Что такое конусное расстояние
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ПЕРЕДАЧИ ЗУБЧАТЫЕ КОНИЧЕСКИЕ С ПРЯМЫМИ ЗУБЬЯМИ
Straight bevel gear pairs.
Calculation of geometry
Дата введения 1975-01-01
Постановлением Государственного комитета стандартов Совета Министров СССР от 28 марта 1974 г. N 718 срок действия установлен с 01.01.75
ПЕРЕИЗДАНИЕ. Май 1990 г.
Настоящий стандарт распространяется на зубчатые конические передачи с прямыми пропорционально понижающимися зубьями внешнего зацепления с внешним окружным модулем более 1 мм, с межосевыми углами от 10 до 170° и с прямолинейным профилем исходного контура, зубчатые колеса которых нарезаются методом обкатки зубострогальными резцами и парными зуборезными головками, а также методом копирования по шаблону.
Стандарт устанавливает метод расчета геометрических параметров зубчатой передачи, а также геометрических параметров зубчатых колес, приводимых на рабочих чертежах.
Стандарт не распространяется на конические зубчатые передачи с прямыми зубьями кругового профиля.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Принципиальная схема расчета геометрии приведена на чертеже.
1.2. Термины и обозначения, примененные в настоящем стандарте, соответствуют ГОСТ 16530-83 и ГОСТ 19325-73.
1.3. Наименования параметров, приводимых на рабочих чертежах зубчатых колес, выделены в таблицах настоящего стандарта полужирным шрифтом.
1.4. При отсутствии в обозначениях параметров индексов «1» и «2», относящихся соответственно к шестерне и колесу, имеется в виду любое зубчатое колесо передачи.
1.5. При отсутствии дополнительных указаний везде, где упоминается профиль зуба, имеется в виду внешний торцовый профиль.
1.6. Расчетом определяются номинальные размеры зубчатой передачи и зубчатых колес.
1.7. Вычисления по формулам стандарта и приложений к нему, за исключением случаев специально отмеченных, должны производиться со следующей точностью:
1.8. Пример расчета приведен в справочном приложении 4.
Что такое конусное расстояние
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ПЕРЕДАЧИ ЗУБЧАТЫЕ КОНИЧЕСКИЕ С КРУГОВЫМИ ЗУБЬЯМИ
Spiral bevel gear pairs. Calculation of geometry
Дата введения 1975-01-01
Утвержден и введен в действие Постановлением Государственного комитета стандартов Совета Министров СССР от 27.12.1973 N 2816.
Разработан Центральным научно-исследовательским институтом технологии машиностроения (ЦНИИТМАШ)
Настоящий стандарт распространяется на передачи зубчатые конические обкатные с круговыми зубьями внешнего зацепления с межосевыми углами от 10 до 150°, углом наклона зуба от 0 до 45° с прямолинейным профилем исходного контура.
Стандарт устанавливает метод расчета геометрических параметров зубчатой передачи, а также геометрических параметров зубчатых колес, приводимых на рабочих чертежах.
Стандарт не распространяется на передачи специального назначения (ведущих мостов автомобилей и тракторов и др.).
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Принципиальная схема расчета геометрии приведена на чертеже.
1.2. Термины и обозначения, примененные в настоящем стандарте, соответствуют ГОСТ 16530-70 и ГОСТ 19325-73.
1.3. Наименования параметров, приводимые на рабочих чертежах зубчатых колес, выделены в таблицах настоящего стандарта полужирным шрифтом.
1.4. При отсутствии в обозначениях параметров индексов «1» и «2», относящихся соответственно к шестерне и колесу, имеется в виду любое зубчатое колесо передачи.
1.5. При отсутствии дополнительных указаний везде, где упоминается профиль зуба, имеется в виду профиль в нормальном расчетном сечении.
1.6. Расчетом определяются номинальные размеры зубчатой передачи и зубчатых колес.
1.7. Вычисления по формулам стандарта и приложений к нему, за исключением случаев специально отмеченных, должны производиться со следующей точностью:
1.8. Примеры расчета приведены в приложении 7.
Принципиальная схема расчета геометрии
2. РАСЧЕТ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ
Исходные данные для расчета
средний нормальный (расчетный)
Угол наклона зуба средний (расчетный)
Направление линии зуба
Средний нормальный исходный контур
Коэффициент высоты головки зуба
Коэффициент радиального зазора
Коэффициент радиуса кривизны переходной кривой в граничной точке профиля зуба
1. Рекомендации по выбору исходных данных приведены в приложении 1.
Расчет основных геометрических параметров
Расчетные формулы и указания
Выбор осевой формы зуба
1. Число зубьев плоского колеса
.
При 
.
2. Среднее конусное расстояние (при заданном )
3. Внешнее конусное расстояние (при заданном )
4. Выбор осевой формы зуба
Рекомендации по выбору осевой формы зуба и диаметра приведены в приложении 2
5. Номинальный диаметр зуборезной головки (шлифовального круга)
Расчет параметров зубчатой передачи
6. Угол делительного конуса
; 
.
При 
, 
.
При 
углы определяются с точностью до 2″.
Углы должны находиться в пределах 5-85°.
7. Ширина зубчатого венца
2. Для передач с параметрами по ГОСТ 12289-66 ширину зубчатого венца принимать по указанному стандарту
8. Передаточное число
9. Передаточное число эквивалентной конической передачи
Определяется для передач с 
10. Число зубьев эквивалентной конической шестерни
Определяется для передач с 
11. Коэффициент смещения у шестерни
Рекомендации по выбору величин и приведены в приложении 3
12. Коэффициент изменения расчетной толщины зуба шестерни
Расчет при заданном среднем нормальном (расчетном) модуле
13. Развод резцов зуборезной головки для чистовой двухсторонней обработки колеса
Если и приняты по табл.2 приложения 1, то принимается по этой же таблице.
.
Вычисленное значение рекомендуется округлить до ближайшего значения по табл.2 приложения 1 или до имеющегося в производстве, соблюдая следующие условия:
а) при 
и 
мм
;
при 
и 
мм
,
кроме того, вычисляется поправка на высоту ножки зуба
;
б) при 
и 
мм
,
кроме того, уточняется принятое в п.12 значение по формуле:
.
Если приведенные в подпунктах а и б неравенства не соблюдаются, то вычисляют новое значение по формуле
.
По полученному значению уточняется значение (п.2) и проводится последующий расчет
14. Расстояние от внешнего торца до расчетного сечения
.
; 
.
При этом величина должна быть в пределах 
.
Если это условие не соблюдается, то следует изменить исходные данные для расчета, например
15. Внешнее конусное расстояние
16. Внешний окружной модуль
Расчет при заданном внешнем окружном модуле
17. Развод резцов зуборезной головки для чистовой двухсторонней обработки колеса
Первоначальный расчет производят при =1, что соответствует расположению расчетного сечения по середине ширины зубчатого венца. Вычисленное значение округляется до значения по ГОСТ 11902-66 или до имеющегося в производстве.
Весь последующий расчет выполняют с учетом новых значений и принятого
18. Расчетный модуль
19. Среднее конусное расстояние
20. Расстояние от внешнего торца до расчетного сечения
Расчет параметров зубчатых колес
Осевая форма зуба I
Осевая форма зуба II
Осевая форма зуба III
21. Высота ножки зуба в расчетном сечении
;
.
Поправка вводится только при 
и двухсторонней обработке колеса и принимается по табл.2 приложения 1 или вычисляется по п.13 настоящей таблицы
22. Нормальная толщина зуба в расчетном сечении
;
23. Сумма углов ножек зубьев шестерни и колеса
Осевая форма зуба I
Осевая форма зуба II
Осевая форма зуба III
При 
(в минутах).
Угол не должен быть больше 900′.
При 
(в минутах),
где 
Значение должно находиться в пределах 0-500 (см. приложение 4).
Значение при 
мм рекомендуется округлять кратно 20
24. Угол ножки зуба
Осевая форма зуба I
Осевая форма зуба II
Осевая форма зуба III
;
;
25. Угол головки зуба
;
;
.
Коэффициенты и при исходном контуре по ГОСТ 16202-70 рекомендуется определять по табл.2 приложения 4.
Если необходимо иметь постоянное значение радиального зазора вдоль ширины венца, то =1.
При этом необходимо проверить степень сужения толщины зуба на поверхности вершин (см. табл.4)
26. Увеличение высоты головки зуба при переходе от расчетного сечения на внешний торец
Осевая форма зуба I
Осевая форма зуба II
Осевая форма зуба III
27. Увеличение высоты ножки зуба при переходе от расчетного сечения на внешний торец
28. Уменьшение высоты головки зуба в расчетном сечении
29. Высота головки зуба в расчетном сечении
; 
30. Внешняя высота головки зуба
31. Внешняя высота ножки зуба
Осевая форма зуба I
Осевая форма зуба II
Осевая форма зуба III
32. Внешняя высота зуба
33. Угол конуса вершин
34. Угол конуса впадин
35. Средний делительный диаметр
36. Внешний делительный диаметр
37. Внешний диаметр вершин зубьев
38. Расстояние от вершины до плоскости внешней
Осевая форма зуба I
Осевая форма зуба II
Осевая форма зуба III
окружности вершин зубьев
При 
.
;
.
Значение принимается с точностью не ниже 0,000001
Что такое конусное расстояние
Тема 4.6. Коническая зубчатая передача
В результате изучения студент должен знать:
— геометрические параметры конической передачи;
— формулы для расчета сил в зацеплении;
— формулы для расчета конических передач на контактную прочность и изгиб.
4.6.1 Общие сведения
Конические зубчатые колёса применяют в передачах, оси валов которых пересекаются под некоторым межосевым углом 
. Обычно 
рис.2.3.17.
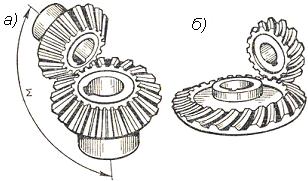
Рисунок 2.3.17 Коническая прямозубая передача а), передача с круговым зубом б)
Применяют во всех отраслях машиностроения, где по условиям компоновки машины необходимо передать движение между пересекающимися осями валов. Конические передачи сложнее цилиндрических, требуют периодической регулировки. Для нарезания зубчатых конических колес необходим специальный инструмент. В сравнении с цилиндрическими конические передачи имеют большую массу и габарит, сложнее в монтаже. Кроме того, одно из конических колёс, как правило шестерня, располагается консольно. При этом, вследствие повышенной деформации консольного вала, увеличиваются неравномерность распределения нагрузки по ширине зубчатого венца и шум.
Конические колёса бывают с прямыми и круговыми зубьями.
Передаточное числа при межосевом угле
(2.3.44)
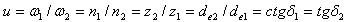
Для конической прямозубой передачи рекомендуется u=2, 2,5; 3,15; 4, для передачи с круговыми зубьями возможны более высокие значения u; наибольшее значение u=6,3.
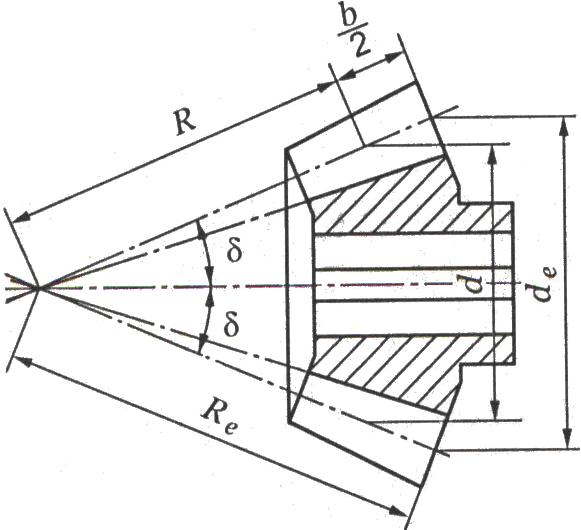
4.6.2 Геометрические параметры конического зубчатого колеса
Основные геометрические размеры определяют в зависимости от модуля и числа зубьев. Высота и толщина зубьев конических колёс постепенно уменьшается по мере приближения к вершине конуса. Соответственно изменяются шаг, модуль и делительные диаметры, которых может быть бесчисленное множество. Основные геометрические размеры имеют обозначения, принятые для прямозубых конических передач рис. 2.3.18.
Рисунок 2.3.18 Геометрия конического колеса
Внешний диаметр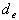 
:
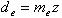
(2.3.45)
где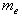 
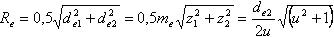
— максимальный модуль зубьев – внешний окружной модуль, полученный по внешнему торцу колеса. Внешнее конусное расстояние
(2.3.46)
Среднее конусное расстояние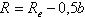 
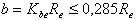
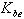
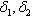
(2.3.47), где b – ширина зубчатого венца колеса 
(2.3.48)
— коэффициент ширины зубчатого венца относительно внешнего конусного расстояния.
— углы делительных конусов;
Средний модуль
(2.3.49)
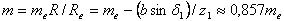
Средние делительные диаметры:
(2.3.50)
(2.3.51)
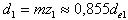
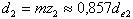
В соответствии с исходным контуром прямозубых конических колёс радиальный зазор c=0,2 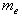, тогда
внешняя высота головки зуба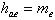 
(2.3.52)
и внешняя высота ножки зуба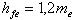 
(2.3.53).
Внешние диаметры вершин зубьев
(2.3.54)
(2.3.55)
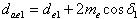
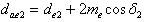
Угол ножки зуба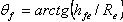 
(2.3.56).
Угол головки зуба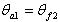 
; 
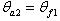
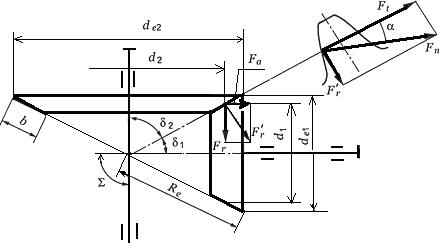
(2.3.57)
4.6.3 Силы в зацеплении конической передачи
Силы в зацеплении определяют по размерам в среднем сечении зуба шестерни. На шестерню конической прямозубой передачи действуют три силы рис.2.3.19:
окружная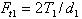 
(2.3.58),
радиальная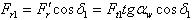 
(2.3.59),
осевая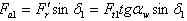 
(2.3.60).
Рисунок 2.3.19 Схема действия сил в зацеплении конических колес
Для колеса направление сил противоположно, при этом:
;
;
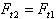
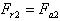
Направление окружных сил F, как и в цилиндрической передаче зависит от направления вращения колёс. Осевые силы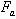 
всегда направлены от вершин конусов, радиальные 
— к осям вращения колёс. Конические передачи с круговыми зубьями получили преимущественное применение. По сравнению с коническими прямозубыми они менее чувствительны к нарушению точности взаимного расположения колёс, их изготовление проще. Недостаток передач с круговыми зубьями – изменение величины и знака осевых сил при реверсе. Ось кругового зуба – это дуга окружности соответствующего диаметра резцовой головки. Нарезание зубьев резцовой головки обеспечивает высокую производительность и низкую стоимость колёс. Угол наклона кругового зуба переменный. За расчётный принимают угол на окружности среднего диаметра колеса, обычно Значение выбирают исходя из обеспечения плавности зацепления.
4.6.4 Расчет на контактную прочность
Прочностной расчет конической передачи основан на допущении, что несущая способность зубьев конического колеса такая же как у эквивалентного цилиндрического. Эквивалентным колесом называется такое цилиндрическое колесо, у которого делительный диаметр и модуль равны делительному диаметру и модулю в среднем нормальном сечении реального конического колеса рис.2.3.20.
Рисунок 2.3.20 Схема построения эквивалентного колеса
Межосевое расстояние эквивалентной передачи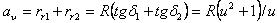 
(2.3.61)
Передаточное число эквивалентной передачи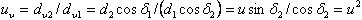 
(2.3.62)
Момент на эквивалентном колесе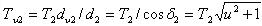 
(2.3.63)
4.6.5 Расчет конических зубчатых передач на изгиб
Формула проверочного расчёта конических прямозубых передач: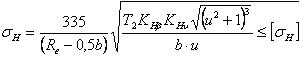 
(2.3.64)
Формула проектировочного расчёта конических прямозубых передач: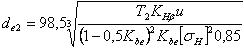 
(2.3.65)
Условие прочности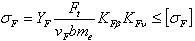 
(2.3.66)
где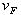 
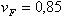
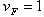
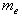
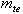
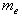
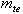
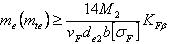
— коэффициент вида конических колёс. Для прямозубых колёс 
; для колёс с круговыми зубьями 
; и 
— внешний и окружёной модули; YF – коэффициент формы зуба. Внешний окружной модуль или определяют расчётом на изгиб по формуле
(2.3.67)
Минимальное число зубьев шестерни z конической передачи с круговыми зубьями определяют по формуле
(2.3.68)