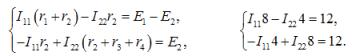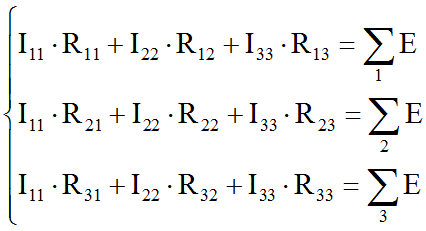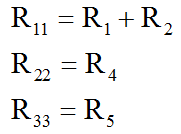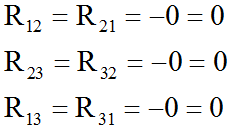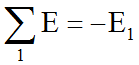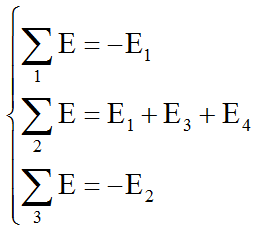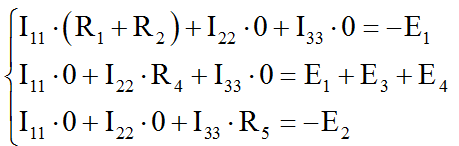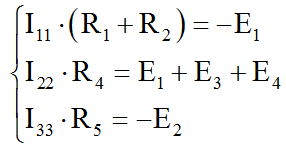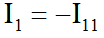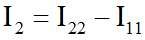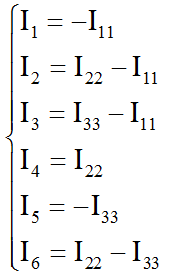Метод контурных токов

Метод контурных токов используется для расчета резистивных линейных цепей с постоянными токами и для расчета комплексных схем замещения линейных цепей с гармоническими токами. При этом в расчет вводятся контурные токи – это фиктивные токи, которые замыкаются в независимых замкнутых контурах, отличающихся друг от друга наличием хотя бы одной новой ветви.

Методика расчета цепи методом контурных токов

В методе контурных токов за неизвестные величины принимаются расчетные (контурные) токи, которые якобы протекают в каждом из независимых контуров. Таким образом, количество неизвестных токов и уравнений в системе равно числу независимых контуров цепи.

Расчет токов ветвей по методу контурных токов выполняют в следующем порядке:

1 Вычерчиваем принципиальную схему цепи и обозначаем все элементы.

2 Определяем все независимые контуры.

3 Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры (I11, I22, I33 и т. д.) или римские цифры.

4 По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учитывать и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.

5 Решаем любым методом полученную систему относительно контурных токов и определяем их.

6 Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры (I1, I2, I3 и т. д.).

7 Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.

При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.

Пример расчёта сложной цепи методом контурных токов

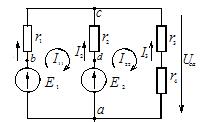
В цепи, изображённой на рисунке 1, рассчитать все токи методом контурных токов. Параметры цепи: Е1 = 24 В, Е2 = 12 В, r1 = r2 = 4 Ом, r3 = 1 Ом, r4 = 3 Ом.

Рис. 1. Схема электрической цепи для примера расчета по методу контурных токов

Решение. Для расчета сложной цепи этим методом достаточно составить два уравнения, по числу независимых контуров. Контурные токи направляем по часовой стрелке и обозначаем I11 и I22 (см. рисунок 1).

По второму закону Кирхгофа относительно контурных токов составляем уравнения:

Решаем систему и получаем контурные токи I11 = I22 = 3 А.

Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. На рисунке 1 такими токами являются I1, I2, I3. Направление у этих токов одинаковое – вертикально вверх.

Переходим от контурных токов к реальным. В первой ветви протекает только один контурный ток I11. Направление его совпадает с направлением реального тока ветви. В таком случае реальный ток I1 + I11 = 3 А.

Следует отметить, как положительный факт, что в методе контурных токов по сравнению с решением по законам Кихгофа пр иходится решать систему уравнений меньшего порядка. Однако этот метод не позволяет сразу определять реальные токи ветвей.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Основы символического метода расчета. Методы контурных токов и узловых потенциалов.

Основные принципы

Любая электротехническая цепь состоит из участков (ветвей), образующих узлы и контуры. Для определения значений тока через любой элемент используют два закона Кирхгофа. Прямое составление уравнений дает систему с их максимальным количеством, равным количеству ветвей. В результате, если множество узлов цепи равно У, а число ветвей Р, то уравнения распределяются следующим образом:

Данное количество избыточно и приводит к образованию громоздкой системы уравнений большой размерности.

Для упрощения расчетов разработаны методики, которые позволяют сократить количество уравнений до приемлемых значений без снижения точности результатов. Наиболее простым является метод контурных токов.

Общий план составления уравнений

1 – Выбор направления действительных токов.

2 – Выбор независимых контуров и направления контурных токов в них.

3 – Определение собственных и общих сопротивлений контуров

4 – Составление уравнений и нахождение контурных токов

5 – Нахождение действительных токов

Итак, после ознакомления с теорией предлагаем приступить к практике! Рассмотрим пример.

Выполняем все поэтапно.

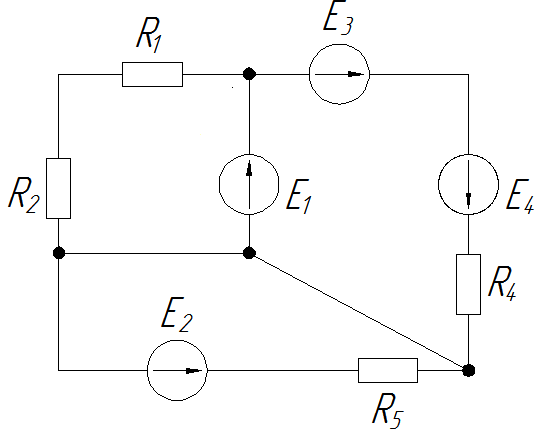
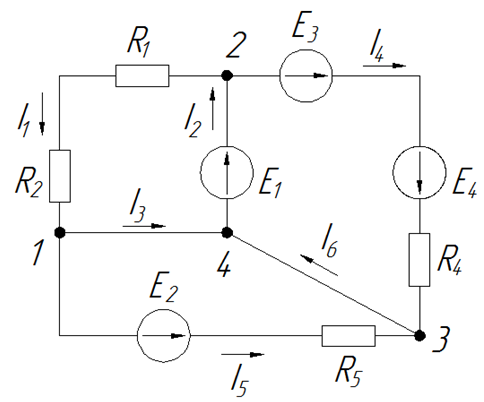
1. Произвольно выбираем направления действительных токов I1-I6.

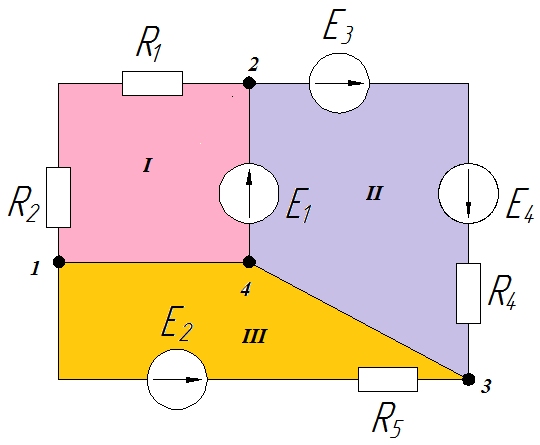
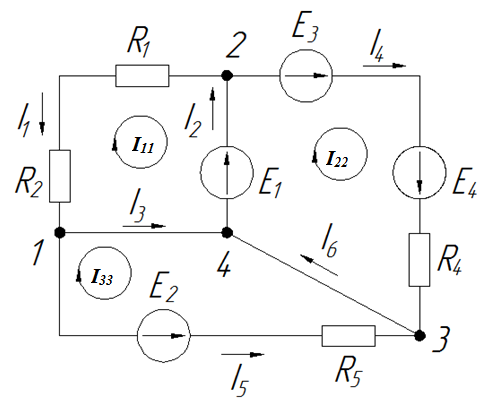
2. Выделяем три контура, а затем указываем направление контурных токов I11,I22,I33. Мы выберем направление по часовой стрелке.

3. Определяем собственные сопротивления контуров. Для этого складываем сопротивления в каждом контуре.

Затем определяем общие сопротивления, общие сопротивления легко обнаружить, они принадлежат сразу нескольким контурам, например сопротивление R4 принадлежит контуру 1 и контуру 2. Поэтому для удобства обозначим такие сопротивления номерами контуров к которым они принадлежат.

4. Приступаем к основному этапу – составлению системы уравнений контурных токов. В левой части уравнений входят падения напряжений в контуре, а в правой ЭДС источников данного контура.

Так как контура у нас три, следовательно, система будет состоять из трех уравнений. Для первого контура уравнение будет выглядеть следующим образом:

Ток первого контура I11, умножаем на собственное сопротивление R11 этого же контура, а затем вычитаем ток I22, помноженный на общее сопротивление первого и второго контуров R21 и ток I33, помноженный на общее сопротивление первого и третьего контура R31. Данное выражение будет равняться ЭДС E1 этого контура. Значение ЭДС берем со знаком плюс, так как направление обхода (по часовой стрелке) совпадает с направление ЭДС, в противном случае нужно было бы брать со знаком минус.

Определение и суть метода контурных токов

Векторная диаграмма токов и напряжений

По данному методу в исследуемой цепи выделяются независимые плоские замкнутые контуры, включающие все, без исключения, элементы. Предполагается, что в каждом контуре может протекать некоторый контурный ток. В том случае, если цепь с элементом принадлежит только одному контуру, то ток через входящие в нее элементы равен контурному. Если элемент охватывается несколькими контурами, то он в ней равен алгебраической (с учетом направления) сумме контурных токов.

Разбиение цепи на контуры

Важно! Суммирование должно производиться строго с учетом направления движения при обходе контура. Знак «плюс» – при совпадении направления, «минус» – при противоположном.

При составлении уравнений учитываются входящие в схему источники ЭДС и тока.

На практике удобнее преобразовать идеальный источник тока в идеальный источник ЭДС. Преобразование выполняется согласно закона Ома:

U=I∙r, где r – внутреннее сопротивление источника тока (напряжения).

Методика расчета используется как в цепях постоянного, так и переменного напряжения. При расчетах цепей переменного напряжения с реактивными элементами используются комплексные величины, затем вычисляются мгновенные и амплитудные величины токов и напряжений и углы сдвига фаз между ними.

Цепь с реактивными элементами

Электротехника Часть 5 Методы расчёта электрических цепей

Всем доброго времени суток. В прошлой статье я рассматривал типы соединений приемников энергии в электрических цепях, а так же законы Кирхгофа, которые определяют основные соотношения токов и напряжений в этих цепях. Но кроме знания основных законов электротехники необходимо уметь рассчитывать неизвестные параметры электрических цепей по заданным известным параметрам. Так, например, по известным напряжениям, ЭДС и сопротивлениям необходимо знать какую мощность будет потреблять тот или иной приемник энергии, а так же вся цепь в целом. Этим мы и займёмся в данной статье.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Построение системы контуров

Основная сложность заключается в правильном выделении контуров. Количество контурных токов будет равняться числу выбранных контуров.

Важно! Каждый элемент схемы должен входить хотя бы в один контур.

Распространены две методики выбора контуров.

Использование планарных графов

Метод планарных графов применяется при ручном расчете, поскольку он наиболее прост и нагляден. Для построения плоского графа схему рисуют таким образом, чтобы не было взаимного пересечения ветвей. Получается, что схему можно разбить на несколько ограниченных участков, которые образуют контуры.

Рассматриваемая методика неприменима без дополнительных преобразований, если невозможно выразить схему в виде планарного графа.

Метод выделения максимального дерева

Метод выделения максимального дерева более абстрактный и используется при автоматизированных расчетах и наличия специализированных программ. Суть метода заключается в исключении из цепи некоторых ветвей в соответствии со строгими правилами, которые таковы:

Построение системы уравнений

Резонанс в электрической цепи

Построение системы уравнений по рассматриваемой методике выполняется по следующим правилам:

После выполнения арифметических действий (раскрытие скобок, приведение подобных слагаемых) получается система уравнений, в которых неизвестными величинами являются виртуальные контурные токи.

Решая систему уравнений, получают значения контурных, а затем искомых величин.

Трехфазные электрические цепи

Трехфазная цепь в рабочем режиме
Среди электрических цепей распространены как однофазные, так и многофазные системы. Каждая часть многофазной цепи характеризуется одинаковым значением тока и называется фазой. Электротехника различает два понятия этого термина. Первое – непосредственная составляющая трехфазной системы. Второе – величина, изменяющаяся синусоидально.

Трехфазная цепь – это одна из многофазных систем переменного тока, где действуют синусоидальные ЭДС (электродвижущая сила) одинаковой частоты, которые сдвинуты во времени относительно друг друга на определенный фазовый угол. Она образована обмотками трехфазного генератора, тремя приемниками электроэнергии и соединительными проводами.

Такие цепи служат для обеспечения генерации электрической энергии, для ее передачи, распределения, и имеет следующие преимущества:

Трехфазная система выгодна при передаче электроэнергии на большие расстояния. К тому же материалоемкость значительно ниже, чем однофазных. Основные потребители – трансформаторы, асинхронные электродвигатели, преобразователи, индукционные печи, мощные нагревательные и силовые установки. Среди однофазных маломощных устройств можно отметить электроинструменты, лампы накаливания, бытовые приборы, блоки питания.

Трехфазная схема отличается значительной уравновешенностью системы. Способы соединения фаз получили структуру «звезда» и «треугольник». Обычно «звездой» соединяются фазы генерирующих электромашин, а фазы потребителей «звездой» и «треугольником».

Оптимизированная процедура составления системы

По упрощенной методике поступают следующим образом:

Формальный подход

Формальный подход предполагает матричную форму записи системы уравнений. Для расчетов исходные данные записывают в матричной форме. Используются такие матрицы:

При составлении матрицы С каждый элемент Сij:

В матрице Z диагональные элементы равняются сопротивлению участков, остальные приравниваются нулю.

Итоговая формула для расчетов имеет вид:

Такая форма записи решения в матричной форме показывает, каким образом выполняются действия над составленными матрицами.

Пример системы уравнений

Ниже рассмотрен пример расчета конкретной схемы без учета номиналов элементов.

Пример решения

В заданной цепи выделяют три контура. Как выразить токи в ветвях через контурные:

Как составить систему уравнений:

Как подставить контурные значения:

После преобразования получается необходимая система уравнений:

Система из трех уравнений легко решается после подстановки известных параметров. Из полученных значений контурных токов затем можно найти искомые величины.

Данный пример решения задач по методу контурных токов показывает, что любую достаточно сложную схему можно существенно упростить для решения, руководствуясь указаниями.

Важно! Метод неприменим, если нет возможности преобразовать цепь без взаимного пересечения ветвей.

В некоторых случаях упростить схему можно путем преобразования ветвей, соединенных по схеме «звезда» в треугольник.

Точно такие же результаты получаются при использовании метода узловых потенциалов. В основе расчетов – поиск потенциала каждого узла (так называемый узловой потенциал). Существуют программы, позволяющие произвести онлайн расчет параметров по рассмотренным методам.

Расчет контурных токов матрица

Рассмотренные методы расчета электрических цепей – непосредственно по законам Кирхгофа, методы контурных токов и узловых потенциалов – позволяют принципиально рассчитать любую схему. Однако их применение без использования введенных ранее топологических матриц рационально для относительно простых схем. Использование матричных методов расчета позволяет формализовать процесс составления уравнений электромагнитного баланса цепи, а также упорядочить ввод данных в ЭВМ, что особенно существенно при расчете сложных разветвленных схем.
Переходя к матричным методам расчета цепей, запишем закон Ома в матричной форме.

Пусть имеем схему по рис. 1, где — источник тока. В соответствии с рассмотренным нами ранее законом Ома для участка цепи с ЭДС для данной схемы можно записать:

Однако, для дальнейших выкладок будет удобнее представить ток как сумму токов k

-й ветви и источника тока, т.е.:

Подставив (2) в (1), получим:

Формула (3) представляет собой аналитическое выражение закона Ома для участка цепи с источниками ЭДС и тока (обобщенной ветви).

Соотношение (3) запишем для всех n

ветвей схемы в виде матричного равенства

– диагональная квадратная (размерностью матрица сопротивлений ветвей, все элементы которой (взаимную индуктивность не учитываем), за исключением элементов главной диагонали, равны нулю.

Соотношение (4) представляет собой матричную запись закона Ома.

Если обе части равенства (4) умножить слева на контурную матрицу В

и учесть второй закон Кирхгофа, согласно которому

то есть получили новую запись в матричной форме второго закона Кирхгофа.

Метод контурных токов в матричной форме

В соответствии с введенным ранее понятием матрицы главных контуров В

,
записываемой для главных контуров, в качестве независимых переменных примем токи ветвей связи, которые и будут равны искомым контурным токам.
Уравнения с контурными токами получаются на основании второго закона Кирхгофа; их число равно числу независимых уравнений, составляемых для контуров, т.е. числу ветвей связи c
=n—m+1
. Выражение (6) запишем следующим образом:

В соответствии с методов контурных токов токи всех ветвей могут быть выражены как линейные комбинации контурных токов или в рассматриваемом случае токов ветвей связи. Если элементы j

–го столбца матрицы
В
умножить соответствующим образом на контурные токи, то сумма таких произведений и будет выражением тока
j
–й ветви через контурные токи (через токи ветвей связи). Сказанное может быть записано в виде матричного соотношения

где — столбцовая матрица контурных токов; — транспонированная контурная матрица.

С учетом (8) соотношение (7) можно записать, как:

Полученное уравнение представляет собой контурные уравнения в

матричной форме. Если обозначить

то получим матричную форму записи уравнений, составленных по методу контурных токов:

где — матрица контурных сопротивлений; — матрица контурных ЭДС.

В развернутой форме (12) можно записать, как:

то есть получили известный из метода контурных токов результат.

Рассмотрим пример составления контурных уравнений.

Пусть имеем схему по рис. 2. Данная схема имеет четыре узла (
m=4)
и шесть обобщенных ветвей
(n=6).
Число независимых контуров, равное числу ветвей связи,

Граф схемы с выбранным деревом (ветви 1, 2, 3) имеет вид по рис. 3.

Запишем матрицу контуров, которая будет являться матрицей главных контуров, поскольку каждая ветвь связи входит только в один контур. Принимая за направление обхода контуров направления ветвей связи, получим:

Диагональная матрица сопротивлений ветвей

Матрица контурных сопротивлений

Матрицы ЭДС и токов источников

Тогда матрица контурных ЭДС

Матрица контурных токов

Таким образом, окончательно получаем:

Анализ результатов показывает, что полученные три уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу контурных токов.

Метод узловых потенциалов в матричной форме

На основании полученного выше соотношения (4), представляющего собой, как было указано, матричную запись закона Ома, запишем матричное выражение:

где — диагональная матрица проводимостей ветвей, все члены которой, за исключением элементов главной диагонали, равны нулю.

Умножив обе части равенства (14) на узловую матрицу А

и учитывая первый закон Кирхгофа, согласно которому

Выражение (16) перепишем, как:

равным нулю, определим напряжения на зажимах ветвей:

Тогда получаем матричное уравнение вида:

Данное уравнение представляет собой узловые уравнения в матричной форме. Если обозначить

то получим матричную форму записи уравнений, составленных по методу узловых потенциалов:

где — матрица узловых проводимостей; — матрица узловых токов.

В развернутом виде соотношение (22) можно записать, как:

то есть получили известный из метода узловых потенциалов результат.

Рассмотрим составление узловых уравнений на примере схемы по рис. 4.

Данная схема имеет 3 узла ( m
=3)
и 5 ветвей (
n=5)
. Граф схемы с выбранной ориентацией ветвей представлен на рис. 5.

Диагональная матрица проводимостей ветвей:

Матрица узловых проводимостей

Матрицы токов и ЭДС источников

Следовательно, матрица узловых токов будет иметь вид:

Таким образом, окончательно получаем:

Анализ результатов показывает, что полученные уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу узловых потенциалов.

Контрольные вопросы и задачи

Составить контурные уравнения для цепи рис. 4, приняв, что дерево образовано ветвями 3

Источник

Метод контурных токов

Сегодня мы разберем еще один важный (и по секрету, наш любимый) метод определения токов в цепи постоянного тока. Это метод контурных токов. На наш взгляд он проще, чем уравнения Кирхгофа, хотя бы потому, что уравнений в системе, которую придется решать, ровно в два раза меньше. Итак, рассмотрим ту же электрическую цепь постоянного тока, которую мы рассчитывали по методу Кирхгофа. Напомним, как выглядит схема

В данной схеме нас интересует количество независимых контуров, выбираем их так же, как мы делали это в прошлый раз. Здесь три независимых контура.

В каждой ветви цепи наносим стрелками направления неизвестных токов, так же, как мы делали ранее (если вы уже рассчитали цепь любым другим способом, то направления и нумерацию токов имеет смысл сохранить, чтобы была возможность сравнить результаты расчета двумя методами). В методе Кирхгофа мы это делали так, повторим.

Подготовительная часть работы завершена, переходим непосредственно к определению токов. Записывается три уравнения (по числу контурных токов). По сути каждое уравнение представляет собой что-то, похожее на второй закон Кирхгофа, только для контурного тока.

В общем виде система уравнений для трех контуров имеет вид

Для всех ветвей системы получается более чем просто:

На примере контура 1: в контуре 1 только один источник напряжения E1, направление которого противоположно направлению контурного тока. Значит,

Для всех контуров получаем

Теперь мы готовы записать и решить полную систему уравнений для трех контурных токов. Получается так:

Упрощая и сокращая то, что упрощается и сокращается, получим несложную систему уравнений с тремя неизвестными, из которой однозначно определяются контурные токи.

Определив контурные токи, мы должны еще определить токи в ветвях. Это делается совсем несложно. Идем по порядку по ветвям нашей цепи и смотрим, как из контурных токов суммируются токи в ветвях. В образовании тока ветви 1 принимает участие только один контурный ток I11, причем он направлен в другую сторону. Значит

Вот и все, задача решена. Остается только сравнить результаты с ответами, полученными другим методом, и убедиться, что все сделано правильно.

Источник