что такое конечно элементная модель
Расчет по методу конечных элементов (МКЭ)
Группа компаний LiraLand
Метод конечных элементов
ЛИРА-САПР это программа для расчета конструкций по методу конечных элементов (МКЭ). В программном комплексе ЛИРА-САПР метод конечных элементов реализован в форме перемещений – МКЭ рассматривается для случаев, когда искомой разрешающей функцией служит перемещение. Это вызвано тем, что выбор расчетной схемы для МКЭ в перемещениях легко поддается алгоритмизации, а практическое использование МКЭ немыслимо без применения современных компьютеров.
Метод конечных элементов основан на мысленном представлении сплошного тела в виде совокупности отдельных конечных элементов, взаимодействующих между собой в конечном числе точек, которые в МКЭ принято называть узлами.
Расчет строительных конструкций с использованием метода конечных элементов (МКЭ) являет собой представление упругих систем в виде набора элементов с конечным числом степеней свободы, которые соединяются между собой в узловых точках (узлах). Такое представление заданной системы приводит к полной формализации всех этапов расчета. Подход к решению задачи является единым, как для стержневых систем, так и для пластин, оболочек, объемных тел и т.п.
Библиотека конечных элементов (БКЭ) содержит элементы, моделирующие работу различных типов конструкций: элементы стержней, четырехугольные и треугольные элементы плоской задачи, плиты, оболочки, элементы пространственной задачи – тетраэдр, параллелепипед, трехгранная призма. Кроме того, в БКЭ имеются различные специальные элементы, моделирующие связь конечной жесткости, упругую податливость между узлами, элементы, задаваемые численной матрицей жесткости.
Библиотека конечных элементов
Перечень типов конечных элементов (КЭ)
В скобках указан признак схемы, где допускается использование КЭ данного типа.
Для линейных задач
Тип 1. Стержневой КЭ плоской фермы (1,2,5)
Тип 2. Стержневой КЭ плоской рамы (2,5)
Тип 3. Стержневой КЭ балочного ростверка (3,5)
Тип 4. Стержневой КЭ пространственной фермы (4,5)
Тип 7. Пространственный стержневой тонкостенный КЭ с учетом депланации сечения (6)
Тип 10. Универсальный пространственный стержневой КЭ (1,2,3,4,5,6)
Тип 11. Прямоугольный КЭ плиты (3,5)
Тип 12. Треугольный КЭ плиты (3,5)
Тип 15. Универсальный прямоугольный КЭ толстой плиты (3,5)
Тип 16. Универсальный треугольный КЭ толстой плиты (3,5)
Тип 17. Универсальный четырехугольный КЭ толстой плиты (3,5)
Тип 19. Четырехугольный КЭ плиты (3,5)
Тип 21. Прямоугольный КЭ плоской задачи (балка-стенка) (1,2,5)
Тип 22. Треугольный КЭ плоской задачи (балка-стенка) (1,2,5)
Тип 23. Универсальный прямоугольный КЭ плоской задачи (балка-стенка) (4,5)
Тип 24. Универсальный треугольный КЭ плоской задачи (балка-стенка) (4,5)
Тип 27. Универсальный четырехугольный КЭ плоской задачи (балка-стенка) (4,5)
Тип 30. Четырехугольный КЭ плоской задачи (балка-стенка) (1,2,5)
Тип 31. Параллелепипед (4,5)
Тип 32. Тетраэдр (4,5)
Тип 33. Прямая треугольная призма (4,5)
Тип 34. Пространственный шестиузловой изопараметрический КЭ (4,5)
Тип 36. Пространственный восьмиузловой изопараметрический КЭ (4,5)
Тип 41. Универсальный прямоугольный КЭ оболочки (5)
Тип 42. Универсальный треугольный КЭ оболочки (5)
Тип 44. Универсальный четырехугольный КЭ оболочки (5)
Тип 45. Универсальный прямоугольный КЭ толстой оболочки (5)
Тип 46. Универсальный треугольный КЭ толстой оболочки (5)/p>
Тип 47. Универсальный четырехугольный КЭ толстой оболочки (5)
Тип 51. Одноузловой КЭ упругой связи (1,2,3,4,5)
Тип 52. КЭ задаваемый численной матрицей жесткости. Конечный элемент, задаваемый численной матрицей жесткости. Применяется для отладки новых типов конечных элементов.
Тип 53. Законтурный двухузловой КЭ упругого основания (3,4,5)
Тип 54. Законтурный одноузловой КЭ упругого основания (3,4,5)
Тип 55. Двухузловой КЭ упругих связей между узлами (1,2,3,4,5)
Тип 56. Одноузловой КЭ упругих связей (1,2,3,4,5)
Тип 57. Одноузловой КЭ одиночной сваи (1,2,3,4,5)
Тип 58. Треугольный КЭ стыка (5)
Тип 59. Четырехугольный КЭ стыка (5)
Тип 60. Двухузловой КЭ многослойного упругого основания (1,2,3,4,5)
Тип 62. Двухузловой КЭ вязкого демпфирования (1,2,3,4,5)
Тип 67. Двухузловой КЭ для моделирования плоского безграничного грунтового массива (1,2,3,4,5)
Тип 68. Треугольный КЭ для моделирования пространственного безграничного грунтового массива (4,5)
Тип 69. Четырехугольный КЭ для моделирования пространственного безграничного грунтового массива (4,5)
Тип 82. Треугольный КЭ плоской задачи (массив) (1,2,5)
Тип 84. Четырехугольный КЭ плоской задачи (массив) (1,2,5)
Для физически нелинейных задач
Тип 201. Физически нелинейный стержневой КЭ плоской фермы (1,2,5)
Тип 202. Физически нелинейный стержневой КЭ плоской рамы (2,5)
Тип 204. Физически нелинейный стержневой КЭ пространственной фермы (4,5)
Тип 207. Физически нелинейный двухузловой КЭ предварительного обжатия (домкрат) (1,2,4,5)
Тип 208. Физически нелинейный двухузловой КЭ предварительного натяжения (1,2,4,5)
Тип 210. Физически нелинейный универсальный пространственный стержневой КЭ (1,2,3,4,5)
Тип 221. Физически нелинейный прямоугольный КЭ плоской задачи (балка-стенка) (1,2,5)
Тип 222. Физически нелинейный треугольный КЭ плоской задачи (балка-стенка) (1,2,5)
Тип 223. Физически нелинейный универсальный прямоугольный КЭ плоской задачи (балка-стенка) (4,5)
Тип 224. Физически нелинейный универсальный треугольный КЭ плоской задачи (балка-стенка) (4,5)
Тип 227. Физически нелинейный универсальный четырехугольный КЭ плоской задачи (балка-стенка) (4,5)
Тип 230. Физически нелинейный четырехугольный КЭ плоской задачи (балка-стенка) (1,2,5)
Тип 231. Физически нелинейный параллелепипед (4,5)
Тип 232. Физически нелинейный тетраэдр (4,5)
Тип 233. Физически нелинейная прямая треугольная призма (4,5)
Тип 234. Физически нелинейный пространственный шестиузловой изопараметрический КЭ (4,5)
Тип 236. Физически нелинейный пространственный восьмиузловой изопараметрический КЭ (4,5)
Тип 241. Физически нелинейный универсальный прямоугольный КЭ оболочки (5)
Тип 242. Физически нелинейный универсальный треугольный КЭ оболочки (5)
Тип 244. Физически нелинейный универсальный четырехугольный КЭ оболочки (5)
Тип 245. Физически нелинейный прямоугольный КЭ толстой оболочки (5)
Тип 246. Физически нелинейный треугольный КЭ толстой оболочки (5)
Тип 247. Физически нелинейный четырехугольный КЭ толстой оболочки (5)
Тип 251. Одноузловой КЭ односторонней связи с учетом предельного усилия (односторонний аналог КЭ 51 с учетом предельного усилия) (1,2,3,4,5)
Тип 252. Двухузловой КЭ односторонней связи с учетом предельного усилия (1,2,3,4,5)
Тип 255. Двухузловой КЭ упругих связей с учетом предельных усилий (аналог КЭ 55 с учетом предельных усилий) (1,2,4,5)
Тип 256. Одноузловой КЭ упругих связей с учетом предельных усилий (аналог КЭ 56 с учетом предельных усилий) (1,2,3,4,5)
Тип 258. Треугольный КЭ стыка с учетом нелинейной работы (аналог КЭ 58 с учетом нелинейной работы) (5)
Тип 259. Четырехугольный КЭ стыка с учетом нелинейной работы (аналог КЭ 59 с учетом нелинейной работы) (5)
Тип 261. Одноузловой КЭ односторонней упругой связи (1,2,3,4,5)
Тип 262. Двухузловой КЭ односторонней упругой связи между узлами (1,2,3,4,5)
Тип 263. Одноузловой КЭ односторонней упругой связи с трением (1,2,4,5)
Тип 264. Двухузловой КЭ односторонней упругой связи с трением между узлами (1,2,4,5)
Тип 265. Двухузловой КЭ односторонних упругих связей (аналог КЭ 55 с учетом односторонней работы) (1,2,4,5)
Тип 266. Одноузловой КЭ односторонних упругих связей (аналог КЭ 56 с учетом односторонней работы) (1,2,3,4,5)
Тип 271. Физически нелинейный параллелепипед (грунт) (4,5)
Тип 272. Физически нелинейный тетраэдр (грунт) (4,5)
Тип 273. Физически нелинейная прямая треугольная призма (грунт) (4,5)
Тип 274. Физически нелинейный пространственный шестиузловой изопараметрический КЭ (грунт) (4,5)
Тип 276. Физически нелинейный пространственный восьмиузловой изопараметрический КЭ (грунт) (4,5)
Тип 281. Физически нелинейный прямоугольный КЭ плоской задачи (грунт) (1,2,5)
Тип 282. Физически нелинейный треугольный КЭ плоской задачи (грунт) (1,2,5)
Тип 284. Физически нелинейный четырехугольный КЭ плоской задачи (грунт) (1,2,5)
Тип 295. Двухузловой КЭ нелинейных упругих связей (аналог КЭ 255 с учетом нелинейной работы) (1,2,4,5)
Тип 296. Одноузловой КЭ нелинейных упругих связей (аналог КЭ 256 с учетом нелинейной работы) (1,2,3,4,5)
Для геометрически нелинейных задач
Тип 308. Геометрически нелинейный двухузловой КЭ для моделирования предварительного натяжения (1,2,4,5)
Тип 309. Геометрически нелинейный универсальный пространственный сильно изгибаемый стержневой КЭ (1,2,3,4,5)
Тип 310. Геометрически нелинейный универсальный пространственный стержневой КЭ (нить) (1,2,3,4,5)
Тип 341. Геометрически нелинейный прямоугольный КЭ оболочки (5)
Тип 342. Геометрически нелинейный треугольный КЭ оболочки (5)
Тип 344. Геометрически нелинейный четырехугольный КЭ оболочки (5)
Для учета физической и геометрической нелинейности
Тип 410. Универсальный пространственный стержневой КЭ с учетом физической и геометрической нелинейности (1,2,3,4,5)
Тип 441. Прямоугольный КЭ оболочки с учетом физической и геометрической нелинейности (5)
Тип 442. Треугольный КЭ оболочки с учетом физической и геометрической нелинейности (5)
Тип 444. Четырехугольный КЭ оболочки с учетом физической и геометрической нелинейности (5)
Для задач теплопроводности
Тип 1505. Стержневой КЭ теплопроводности (15)
Тип 1508. Треугольный КЭ теплопроводности (15)
Тип 1509. Четырехугольный КЭ теплопроводности (15)
Тип 1512. КЭ теплопроводности в форме тетраэдра (15)
Тип 1514. Объемный шестиузловой КЭ теплопроводности (15)
Тип 1516. Объемный восьмиузловой КЭ теплопроводности (15)
Тип 1551. Одноузловой КЭ конвективного теплообмена (15)
Тип 1555. Двухузловой КЭ конвективного теплообмена (15)
Тип 1558. Треугольный КЭ конвективного теплообмена (15)
Тип 1559. Четырехугольный КЭ конвективного теплообмена (15)
Расчет строительных конструкций в ПК ЛИРА-САПР происходит по методу конечных элементов (МКЭ).
Решение линейных задач
Линейный процессор предназначен для решения линейных задач.
В линейных задачах существует линейная зависимость между нагрузками и перемещениями вследствие малости перемещений. Напряжения (усилия) и деформации связаны также линейным законом Гука. Поэтому для линейных задач справедлив принцип суперпозиции и независимости действия сил.
В программном комплексе ЛИРА-САПР реализовано решение линейных задач.
Решение нелинейных задач
Нелинейный процессор предназначен для решения физически и геометрически нелинейных, а также задач с наличием конструктивной нелинейности и предварительного напряжения.
В физически нелинейных задачах отсутствует линейная зависимость между напряжениями и деформациями. Материал конструкции подчиняется нелинейному закону деформирования (нелинейная упругость). Закон деформирования может быть симметричным и несимметричным – с различными пределами сопротивления растяжению и сжатию. Решение этих задач производится шаговым методом.
В геометрически нелинейных задачах отсутствует линейная зависимость между деформациями и перемещениями. На практике наибольшее распространение имеет случай больших перемещений при малых деформациях. Решение этих задач производится шаговым методом, причем шаг выбирается автоматически.
В задачах конструктивной нелинейности имеет место изменение расчетной схемы по мере деформирования конструкции. Так, например, в контактных задачах при достижении некоторой точкой конструкции определенной величины перемещения возникает контакт этой точки с опорой.
В задачах генетической нелинейности учитывается накопление напряжений и деформаций в процессе возведения сооружения (генетическую либо родословную нелинейность, можно рассматривать как вариант конструктивной нелинейности).
Расчет в нелинейной постановке используется как правило для исследования работы уникальных конструкций не имеющих аналогов. Для косвенного учета нелинейных свойств конструкции разработан метод инженерная нелинейность, который позволяет определить пониженную жесткость элементов с последующим проведением расчета по традиционной схеме.
В программном комплексе ЛИРА-САПР реализовано решение физически-, геометрически-, конструктивно-, инженерно-, а также генетически-нелинейных задач.
Контрольные (верификационные) тесты
Программа для проектирования и расчета строительных конструкций ЛИРА-САПР имеет свидетельство о верификации РААСН.
Особое внимание мы уделяем точности и достоверности полученных результатов расчета. Поэтому реализация новых возможностей требует от нас тщательной проверки результатов, в сравнении с раннее известными аналитическими решениями данного класса задач, а также в сравнении результатов с другим программным обеспечением, которое используется для решения инженерных задач.
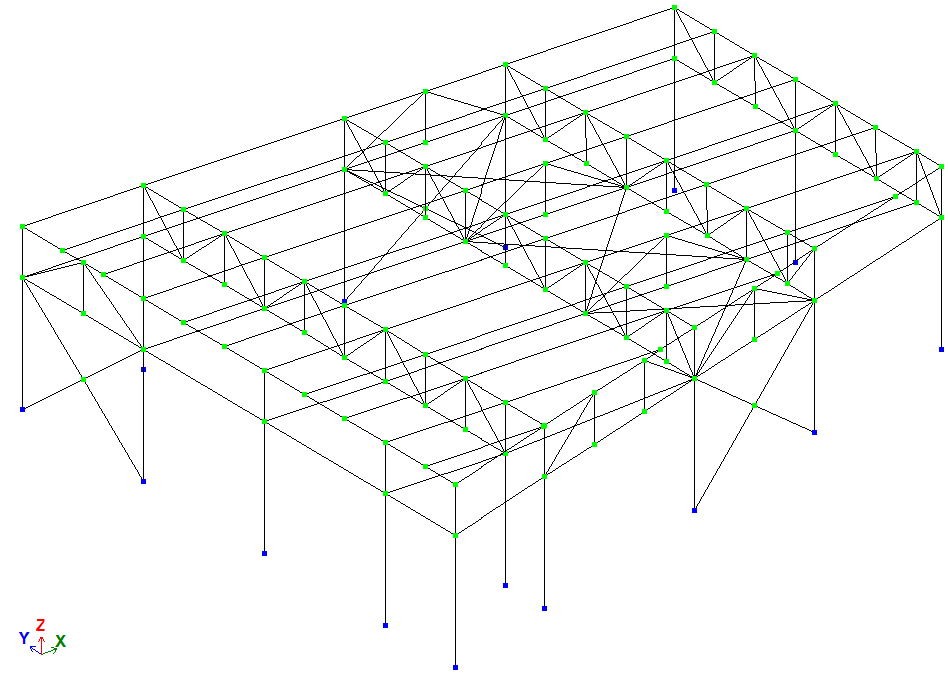
Принципы построения конечно-элементных моделей
Любая строительная конструкция представляется в виде расчетной схемы. Расчетная схема выступает в виде идеализированной модели.
Модель разбивается на конечные элементы. В результате такой разбивки появляются узлы, которые указывают на соединение элементов. В опорные узлы вводятся соответствующие связи, которые обеспечивают соединение с неподвижным основанием. Нумерация узлов и элементов определяет последовательность задания исходной информации и чтение результатов счета. Конечные элементы, имеющие одинаковые жесткостные характеристики, объединяются по типам жесткости.
Координаты расчетной схемы
Расчетная схема располагается в правой декартовой системе координат X, U, Z. Для фиксации местоположения конечного элемента в схеме служит местная система координат – X1, U1, Z1. Местная система координат необходима для ориентации местной нагрузки, главных осей инерции в сечении стержня, усилий и напряжений, возникающих в элементе.
Каждый узел схемы имеет свою локальную систему координат – X2, U2, Z2, которая является правой декартовой, как и местная система. По умолчанию локальная система координат узла совпадает с глобальной.
Локальная система координат узла позволяет задавать нагрузки и заданные перемещения в направлении, не совпадающем с глобальными осями.
Каждый узел схемы в общем случае имеет 6 степеней свободы: три линейных перемещения вдоль осей X или X2; U или U2; Z или Z2 и три поворота вокруг X или X2, U или U2, Z или Z2.
Для расчетных схем, в которых количество степеней свободы в узле заведомо меньше 6 (плоские фермы, плоские рамы и т.п.), применяется так называемый признак схемы. В ПК “ЛИРА” задействованы пять признаков схемы. Признак 1 – 3 – для двухмерных задач, а признак 4 и 5 – для трехмерной задачи.
Признак 2 – схемы, располагаемые в плоскости XOZ; каждый узел имеет 3 степени свободы – линейные перемещения вдоль осей X, Z или X2, Z2 и поворот вокруг оси Y или Y2. В этом признаке схемы рассчитываются плоские рамы и допускается включение элементов ферм и балок-стенок.
Признак 3 – схемы, располагаемые в плоскости XOY; каждый узел имеет 3 степени свободы – линейное перемещение вдоль оси, Z или Z2 и повороты вокруг осей X, Y или X2, Y2. В этом признаке рассчитываются балочные ростверки и плиты; допускается учет упругого основания.
Признак 4 – пространственные схемы, каждый узел которых имеет 3степени свободы – линейные перемещения вдоль осей X, Y, Z или X2, Y2, Z2. В этом признаке рассчитываются пространственные фермы и объемные тела.
Признак 5 – пространственные схемы общего вида с 6 степенями свободы в узле. В этом признаке схемы рассчитываются пространственные каркасы, оболочки и допускается включение объемных тел, учет упругого основания и т.п.
Граничные условия в расчетной схеме могут быть заданы непосредственно на узел, а также смоделированы при помощи связей конечной жесткости.
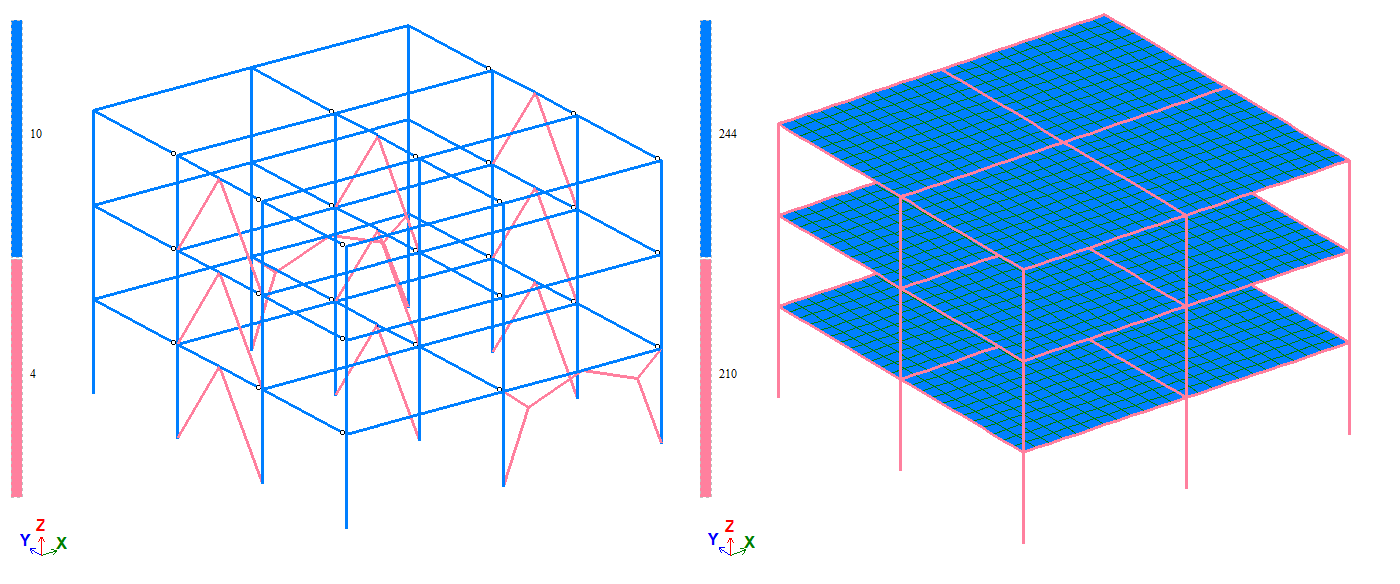
Построение расчетной модели
Представляя расчетную схему сооружения в виде конечно-элементной модели, пользователь всегда стремится достичь компромисса между двумя противоречивыми желаниями: получить как можно более точное решение задачи и за короткое время. Желательно также получить обозримый объем результатов. Для достижения такого компромисса необходимо уметь оценивать оба указанных фактора. Так, время решения задачи легко прогнозируется по количеству узлов, элементов, загружений, а также быстродействию компьютера. ПК “ЛИРА” автоматически дает прогноз времени решения задачи для всех этапов расчета. Однако оценка точности решения задачи является вопросом очень сложным, так как зависит от многих слабо формулируемых факторов:
· густота сетки– с одной стороны, сгущение сетки повышает точность, с другой – неограниченное сгущение может повлечь слабую обусловленность матрицы канонических уравнений и потерю точности;
· физико-механические свойства расчётной модели– расчетная схема может быть близка к геометрически изменяемой, содержать элементы с сильно различающимися жесткостями, что также влечет за собой потерю точности;
· геометрия конечных элементов– если стороны элементов сильно различаются по длине, то это приведет к плохой обусловленности
матрицы накопленных уравнений и также к потере точности;
· свойство конечных элементов– использование высокоточных элементов часто приводит к более точному решению, чем использование простых элементов на значительно более густой сетке.
Назначение сетки надо проводить на основе многих факторов. Так, например, густоту сетки предпочтительно увеличивать только в местах предполагаемого большого градиента напряжений (входящие узлы, места сосредоточенных нагрузок и т.п.). Кроме того, знание свойств конечных элементов также часто помогает рационально построить конечную модель.
Иногда приходится решать большие задачи, в которых густая сетка недопустима из-за ограниченных ресурсов компьютера, а укрупненная разбивка не дает достаточно полной картины напряженно- деформированного состояния конструкции. В этом случае предлагается совместить укрупненную и густую сетку.
Решая задачу несколько раз, можно использовать расчет укрупненной схемы с последующей фрагментацией ее частей.
Фрагментация заключается в последовательном вырезании, уменьшении и детальном расчете некой области конструкции. Такой подход применяется при исследовании областей концентрации напряжений – вокруг отверстий, в местах резкого изменения сечений элементов и т.д. Этот подход применим также при решении больших задач. Первоначально рассчитывается схема из укрупненных конечных элементов. Затем вырезаются отдельные фрагменты этой схемы и дробятся более мелко. Расчет фрагмента производится на воздействия, полученные в результате расчета крупной схемы.
Итак, пусть есть абстрактная задача найти некоторую зависимость y от x в интервале от a до b. Можно поступить двояко – 1) искать аналитический вид зависимости в виде функции y=y(x), т.е. в виде некоторой формулы, как например, все делали в школе, когда брали интеграл, или 2) искать функцию в виде набора точек с некоторой нужной или заданной точностью.
Так, например, на рисунке выше показана некоторая искомая функция y=y(x), вместо которой найдена ломаная 1-2-3-4-5-6 без особого ущерба для точности. Понятно, что чем в большем числе точек искать значение функции, тем точнее будет результат ее представления ломаной. А методы, которые вместо аналитической зависимости находят искомую функцию (или много функций) в виде конечного числа точек (чисел), называются численными.
Введение в метод конечных элементов
В реальных конструкциях почти всегда присутствуют сложные формы, состоящие к тому же из различных материалов. В качестве примера рассмотрим задачи. представленные на рис. 8.2. Рассчитать распределение напряжений в кронштейне (рис. 8.2, о) при помощи аналитических методов крайне сложно. Если же кронштейн изготовлен из композитного материала со сложными свойствами, задача становится практически неразрешимой. Непреодолимые затруднения возникают и при попытке вывести аналитическое выражение для распределения температур в объекте, изображенном на рис. 8.2, б.
Метод конечных элементов, по всей видимости, является наиболее популярным численным методом решения таких задач. Универсальность этого метода удовлетворяет требованиям современных сложных систем конструирования, для которых обычно отсутствуют замкнутые решения уравнений равновесия. Анализ методом конечных элементов начинается с аппроксимации исследуемой области (области задачи) и делении ее на ячейки сетки. На рис. 8.3, а по углам каждой ячейки находятся узлы (черные точки). Такие ячейки и называются конечными элементами. На рис. 8.3, а, б представлены аппроксимации объектов с рис. 8.2, а, б наборами конечных элементов (треугольных и четырехугольных).
В этом примере мы аппроксимировали исходный объект треугольниками и четырехугольниками, однако возможны и конечные элементы других типов. Выбор элементов определяется областью задачи, ее типом, а также конкретным пакетом анализа. Выбор подходящих элементов с нужным количеством узлов из библиотеки доступных элементов является одним из наиболее важных решений, которые приходится принимать пользователю пакета конечноэлементного анализа. Конструктору также приходится задавать полное количество элементов (другими словами, их размер). Общее правило состоит в том, что чем больше количество узлов и элементов (в h-версии) или чем выше степень функции формы (в р-версии), тем точнее оказывается решение, но тем дороже оно стоит с вычислительной точки зрения. Другая проблема — построение сетки, особенно для объекта сложной геометрии. Создание трехмерных сеток конечных элементов обычно представляет собой трудоемкий и кропотливый процесс. Сейчас ведутся активные разработки систем автоматизированного построения сеток, которые могли бы подключаться к системам геометрического моделирования. Такие системы позволили бы полностью интегрировать средства CAM и CAE.
После аппроксимации исходного объекта конечными элементами с должным количеством узлов каждому узлу сопоставляется неизвестная величина, которая ищется в процессе решения задачи. Например, для рис. 8.3, а неизвестными были бы смещения узлов по координатам х и у. Отсюда следует, что у каждого узла будет две степени свободы, а у задачи в целом будет 2п степеней свободы, если число узлов равно п. В разделе 8.2 мы покажем, что смещение в любой точке конечного элемента выводится из смещений его узлов при помощи функций формы, поэтому неизвестными могут быть только смещения узлов. Функции формы служат лишь для того, чтобы вычислять значения неизвестных внутри элемента по заданным значениям на его узлах. После вычисления смещений программа может перейти к расчету деформаций как частных производных от функции смещения, а по деформациям рассчитываются напряжения.
Аппроксимировав область задачи набором дискретных конечных элементов, мы должны задать характеристики материала и граничные условия для каждого элемента. Указав различные характеристики для разных элементов, мы можем анализировать поведение объекта, состоящего из разных материалов. Граничные условия (смещение, внешняя сила или температура) обычно задаются на внешней границе объекта. Эти условия должны быть выражены в виде значений смещения, силы или температуры в граничных узлах некоторых конечных элементов. После задания граничных условий для всех внешних узлов программа конечноэлементного анализа формирует систему уравнений, связывающую граничные условия с неизвестными (смещениями или температурой в узлах или коэффициентами функции формы в р-версии), после чего решает эту систему относительно неизвестных.
После нахождения значений неизвестных пользователь получает возможность рассчитать значение любого параметра в любой точке любого конечного элемента по той же функции формы, которая использовалась при построении системы уравнений. Выходные данные программы анализа методом конечных элементов обычно представляются в числовой форме. В задачах механики твердых тел выходными данными являются смещения и напряжения. В задачах на тепло перенос выходными данными являются температуры и тепловые потоки через конкретные элементы. Однако по числовым данным пользователю бывает затруднительно получить общее представление о поведении соответствующих параметров. Графические изображения обычно более информативны, поскольку дают возможность изучить поведение параметров на всей области задачи. Анализ поведения параметров может производиться при помощи постпроцессора, который строит кривые и контурные графики переменных по данным программы конечноэлементного анализа. Для задач строительной механики возможно отображение деформированных тел вместе с недеформированными. В этой области для систем автоматизированного конструирования очень важными становятся функции компьютерной графики.
Многие конструкторы страдают чрезмерной верой в мощь этого метода, не имея представления о его ограничениях; они принимают неправильные результаты без тени сомнения. К преимуществам метода конечных элементов относится возможность работы с телами произвольной геометрии и неоднородными материалами. Однако суть метода состоит в делении области задачи на набор конечных элементов и поиске наилучшего решения, непрерывного «внутри» элементов, но имеющего возможность претерпевать скачки на их границах. Например, деформация на границе конечных элементов кронштейна (рис. 8.3, а),может испытывать скачок, невозможный с точки зрения физики. Величина такого скачка часто служит мерой точности решения, полученного методом конечных элементов. Неточности такого рода зависят от количества элементов, их размера и степени функции формы, используемой внутри каждого из элементов.
Дата добавления: 2015-09-29 ; просмотров: 6018 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ