что такое композиция в математике

Что же такое Композиция Функций?

«Композиция» — (от лат. compositio — составление — связывание) объединение, составление, сопоставление, расположение, сложение, соединение частей в единое целое в определенном порядке.

Толковый словарь здравого смысла

В математике композиция функций (суперпози́ция фу́нкций) — это применение одной функции к результату другой.

Материал из Википедии — свободной энциклопедии

Если функции f(x) и g(x) заданы своими выражениями, то для получения выражения композиции этих функций надо подставить в выражение функции g(x) вместо x выражение функции f(x).

Определение композиции функций из школьного учебника

Давай те же разберемся, что такое композиция функций в переводе на нормальный, человеческий язык. Исходя из первого определения, мы видим, что композицией функций можно назвать их объединение, сопоставление, соединение частей двух функций в единое целое в определенном порядке. Как же происходит это соединение? Обратимся к определению из учебника: … для получения выражения композиции функций надо подставить в выражение функции g(x) вместо x выражение функции f(x).

Для понимания смысла этой фразы рассмотрим пример:

Пусть даны две функции f(x)=x²+1 и g(x)= 1/x,

для нахождения их композиции заменим в выражении 1/x переменную x на x²+1. В результате мы получаем, что

Следует заметить, что композиции g ○ f и f ○ g — это совершенно разные вещи, и при решении ЕГЭ не стоит их путать.

Таким образом на примере мы убедились, что в определении композиции функций нет ничего сложного, и теперь вы с легкостью можете совершать любые операции над функциями.

Источник

Композиция отображений

Компози́ция фу́нкций (суперпози́ция фу́нкций) в математике — это применение одной функции к результату другой.

Композиция функций F и G обычно обозначается .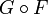

Содержание

Определение

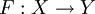
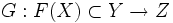
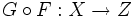
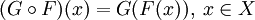
Пусть и две функции. Тогда их композицией называется функция , определённая равенством:

.

Связанные определения

Свойства композиции

Дополнительные свойства

Полезное

Смотреть что такое «Композиция отображений» в других словарях:

Функция (математика) — У этого термина существуют и другие значения, см. функция. Запрос «Отображение» перенаправляется сюда; см. также другие значения … Википедия

ХОПФА ИНВАРИАНТ — инвариант гомотопич. класса отображений топологич. пространств. Впервые был определенX. Хопфом ([1], [2]) для отображений сфер Пусть непрерывное отображение. Переходя, если нужно, к гомотопному отображению, можно считать это отображение… … Математическая энциклопедия

МЕРОМОРФНОЕ ОТОБРАЖЕНИЕ — комплексных пространств обобщение понятия мероморфной функции. Пусть Xи Y комплексные пространства, А открытое подмножество в X такое, что нигде не плотное аналитич. одмпожество, и пусть дано аналитич. отображение Отображение f наз. мероморфным… … Математическая энциклопедия

ПОЧТИКОЛЬЦО — одно из обобщений понятия ассоциативного кольца. П. это кольцоид над группой, т. е. универсальная алгебра, в к рой имеется ассоциативная операция умножения и операция сложения; относительно сложения П. должно быть группой (не обязательно… … Математическая энциклопедия

ОПЕРАТОР — отображение одного множества на другое, каждое из к рых наделено нек рой структурой (алгебраич. операциями, топологией, отношением порядка). Общее определение О. совпадает с определением отображения или функции: пусть Xи Y два множества;… … Математическая энциклопедия

Непрерывное отображение — или непрерывная функция в математике это отображение из одного пространства в другое, при котором близкие точки области определения переходят в близкие точки области значений. Наиболее общее определение формулируется для отображений… … Википедия

ГОМОЛОГИИ ТЕОРИЯ — топологических пространств часть алгебраич. топологии, осуществляющая связь между топологич. н алгебраич. понятиями: приводя в соответствие каждому пространству определенную последовательность групп, а непрерывному отображению пространств… … Математическая энциклопедия

Источник

Композиция функций

В математике компози́ция фу́нкций (суперпози́ция фу́нкций) — это применение одной функции к результату другой.

Композиция функций и обычно обозначается .

Содержание

Определение

Пусть и две функции. Тогда их композицией называется функция , определённая равенством:

.

Связанные определения

Свойства композиции

Дополнительные свойства

Полезное

Смотреть что такое «Композиция функций» в других словарях:

Композиция — (лат. compositio составление, связывание, сложение, соединение): В Викисловаре есть статья «композиция» Искусство Композиция (изобразительное искусство) организующий компонент художественной формы, придающий прои … Википедия

Композиция (теория чисел) — У этого термина существуют и другие значения, см. Композиция. Не следует путать с Композиция функций. В теории чисел композицией натурального числа называется его представление в виде упорядоченной суммы натуральных слагаемых. Слагаемые, входящие … Википедия

Композиция числа — У этого термина существуют и другие значения, см. Композиция. Не следует путать с Композиция функций. В теории чисел композицией, или разложением, натурального числа называется его представление в виде упорядоченной суммы натуральных слагаемых.… … Википедия

Композиция (матем.) — Композиция (математическое), общее название для операции, производящей из двух элементов а и b третий элемент с = а*b. Например, К. двух функций f (x) и g (x) называют функцию h (x) = f [g (x)]. В математическом анализе и теории вероятностей К.… … Большая советская энциклопедия

Композиция — I Композиция (от лат. compositio составление, сочинение) 1) построение художественного произведения, обусловленное его содержанием, характером и назначением и во многом определяющее его восприятие. К. важнейший организующий компонент… … Большая советская энциклопедия

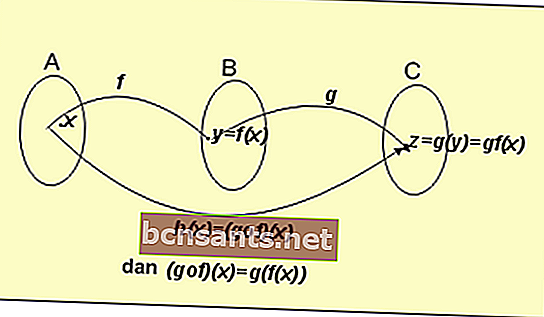
КОМПОЗИЦИЯ — бинарная алгебраическая операция. Напр., К. (или суперпозицией) двух функций f(x)и g(x)наз. функция h(x)=f[g

Свойства функций, непрерывных в точке — Непрерывное отображение или непрерывная функция это такое отображение, у которого небольшие изменения аргумента приводят к небольшим изменениям значения отображения. Это понятие определятся немного по разному в различных разделах математики;… … Википедия

Угроза (шахматная композиция) — У этого термина существуют и другие значения, см. Угроза (значения). Угроза (англ. threat), в шахматной композиции игра, возникающая после сделанного хода, которая, без учёта ответного хода противоположной стороны, приводит к выполнению… … Википедия

СУПЕРПОЗИЦИЯ ФУНКЦИИ — композиция функций, составление из двух функций сложной функции … Математическая энциклопедия

Источник

Композиция (матем.)

Смотреть что такое «Композиция (матем.)» в других словарях:

Группа (матем.) — Группа, одно из основных понятий современной математики. Теория Г. изучает в самой общей форме свойства действий, наиболее часто встречающихся в математике и её приложениях (примеры таких действий ≈ умножение чисел, сложение векторов,… … Большая советская энциклопедия

СЛОЖНАЯ ФУНКЦИЯ — функция, представленная как композиция нескольких функций. Если множество значений Yi функции fi содержится во множестве определения Х i+1 функции fi+1, т. е. то функция определяемая равенством наз. сложной функцией или (п 1) кратной композицией… … Математическая энциклопедия

ИНДЕКСА ФОРМУЛЫ — соотношения между аналитич. и топологич. инвариантами операторов нек рого класса. Именно, И. ф. устанавливают связь между аналитич. индексом линейного оператора (L0, L1 топологич. векторные пространства), определяемым формулой и измеряющим таким… … Математическая энциклопедия

ГРУППА — множество, на к ром определена операция, наз. умножением и удовлетворяющая спец. условиям (групповым аксиомам): в Г. существует единичный элемент; для каждого элемента Г. существует обратный; операция умножения ассоциативна. Понятие Г. возникло… … Физическая энциклопедия

Математические задачи на шахматной доске — Математические задачи на шахматной доске. Шахматная доска с расположенными на ней фигурами и ходы фигур послужили удобной моделью, породившей ряд математических задач, в том числе и таких, которыми занимались известные математики. Наиболее… … Википедия

ИЗОГЕНИЯ — эпиморфизм групповых схем с конечным ядром. Морфизм групповых схем f : над базисной схемой S наз. изогенией, если f сюръективен и его ядро Кег(f) есть плоская конечная групповая S схема. В дальнейшем предполагается, что S есть спектр поля… … Математическая энциклопедия

ПОЛУГРУППА ОПЕРАТОРОВ — семейство операторов <Т>вбанаховом или топологическом векторном пространстве, обладающее тем свойством, что композиция любых двух операторов семейства снова принадлежит семейству. Если операторы Т занумерованы элементами нек рой абстрактной… … Математическая энциклопедия

КУБИЧЕСКАЯ ГИПЕРПОВЕРХНОСТЬ — проективное алгебраич. многообразие, задаваемое однородным уравнением 3 й степени с коэффициентами из нек рого основного поля k. Кубические кривые. Неприводимая кубич. кривая является либо гладкой (в этом случае ее канонич. класс равен 0, а род… … Математическая энциклопедия

АЛГЕБРА — часть математики, посвященная изучению алгебраических операций. Исторический очерк. Простейшие алгебраич. операции арифметич. действия над натуральными и положительными рациональными числами встречаются в самых ранних математич. текстах,… … Математическая энциклопедия

АЛГОРИТМОВ СОЧЕТАНИЯ — название, установившееся за рядом конкретных способов конструирования новых алгоритмов из нескольких заданных. В применении к нормальным алгорифмам наибольшую известность получили следующие А. с.: нормальная композиция двух нормальных алгорифмов … Математическая энциклопедия

Источник

Композиционные функции: основные понятия, формулы и примеры

Формулы функции композиции

В композиции функция также известна как отдельная функция.

Что такое отдельная функция?

Тогда функция (fog) (x) = f (g (x)) → функция g (x) составляется как функция f (x)

Чтобы понять эту функцию, рассмотрите изображение ниже:

Из приведенной выше схемы формул мы получили следующее определение:

Если f: A → B определяется формулой y = f (x)

Если g: B → C определяется формулой y = g (x)

Тогда мы получаем результат функций g и f:

h (x) = (gof) (x) = g (f (x))

Из приведенного выше определения можно сделать вывод, что функции, включающие функции f и g, можно записать:

Свойства функции композиции

У функции композиции есть несколько свойств, которые описаны ниже.

Если f: A → B, g: B → C, h: C → D, то:

Пример проблем

Проблема 1

Даны две функции, каждая f (x) и g (x), соответственно, а именно:

е (х) = 3х + 2

а) ( ф о г ) (х)

б) ( г о ж ) (х)

Ответ

е (х) = 3х + 2

( ф о г ) (х)

«Подключите g (x) к f (x)»

( ж о г ) (х) = е ( г (х))

( г о ж ) (х)

«Подключите f (x) к g (x)»

( ж о г ) (х) = г ( е (х))

= г (3x + 2)

Проблема 2

Если известно, что f (x) = 3x + 4 и g (x) = 3x, каково значение (fog) (2).

Ответ:

Проблема 3

Ответ

( g o f ) (1) =…?

Вставьте f (x) в g (x), затем заполните 1

Проблема 4

Ему даны две функции:

Если (туман) (а) равно 33, найдите значение 5а.

Ответ:

Искать сначала (туман) (x)

(туман) (x) равно 2 × 2 4x + 6-3

(туман) (x) равно 2 × 2 4x + 3

33 то же самое, что 2a2 4a + 3

Также прочтите: Бизнес-формулы: объяснение материала, примеры вопросов и обсуждение

5a = 5 (−5) = −25 или 5a = 5 (3) = 15

Проблема 5

Ответ:

(туман) (x) равно x² + 3x + 4

f (g (x)) равно x² + 3x + 4

f (g (x)) = x² + 3x + 4 и для g (x), равного 3, получаем x равным 2

Пока: f (3) = 2² + 3. 2 + 4 = 4 + 6 + 4 = 14

Таким образом, объяснение формулы функции композиции является примером проблемы. Может быть полезно.

Источник