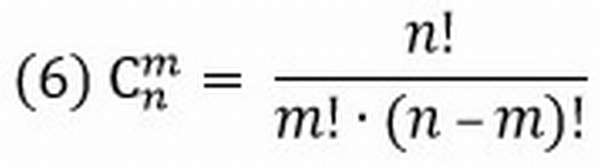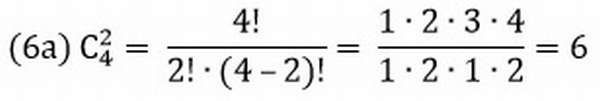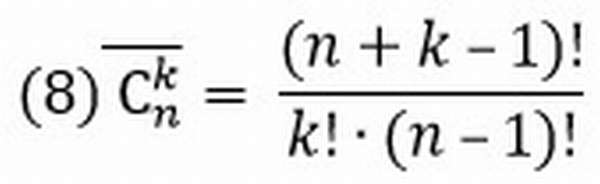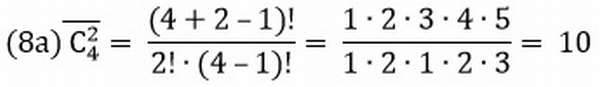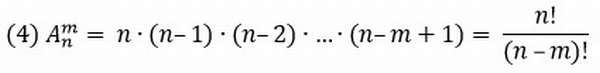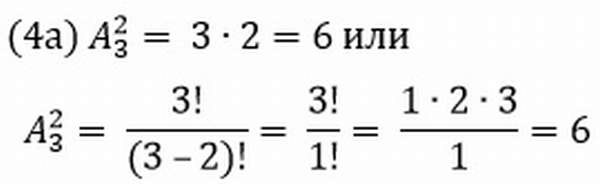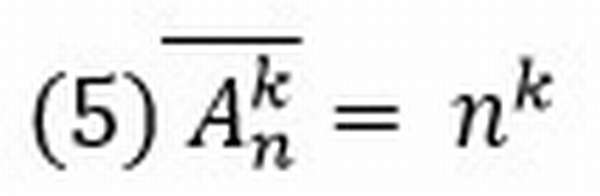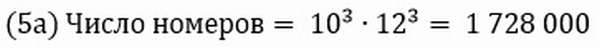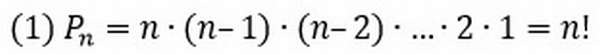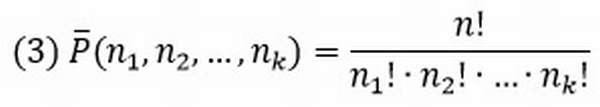что такое комбинаторные методы
Комбинаторика основные понятия и формулы с примерами
Комбинаторика — раздел математики. Основные понятия и формулы комбинаторики как науки применяются во всех сферах жизни.
Неудивительно, что она включена в программу 11 класса, а также во вступительные испытания во многих ВУЗах РФ. Ее основы лежат в прикладном искусстве многих сфер деятельности человека.
Ее история насчитывает более 6 веков. Первые комбинаторные задачи появились в трудах философов и математиков Средневековья.
Представители того научного мира пытались найти методы решения таких задач, их базовые правила и понятия, утвердить уникальные формулы и уравнения для тех, кто ещё не встречался с ними. Такая информация в наше время называется информацией «для чайников».
Попытаемся разобраться в аспектах этой области науки: каковы элементы, свойства, правила, методы и основное ее применение в нашей жизни? Конечно, всю область в одной статье невозможно охватить. Поэтому ниже будет представлено всё самое основное.
Что такое комбинаторика в математике
Суть этого термина дают книги прошлых лет: это раздел математики, занимающийся операциями со множеством элементов.
В интернете есть учебники по информатике и математике для детей, школьников, сборники материалов и задач для начинающих, где в доступном виде объяснена «занимательная» комбинаторика. Нужно твердо выяснить, как решать подобные задачи.
В младших классах задачи на эту тему решают на дополнительных кружках, а в школах с углубленным изучением математики на основных уроках. К тому же, задачи по комбинаторике включены в олимпиады всех уровней.
Основные понятия
Правило произведения
Является одним из основных правил при решении таких задач и звучит так:
При выборе элемента А из n способов и выборе элемента В из m способов верно утверждение, что выбрать пару А и В одновременно можно n*m способами.
Рассмотрим на конкретных примерах.
Задача №1.
В коробке лежит 2 мяча и 6 скакалок. Сколько существует способов достать 1 мяч и 1 скакалку?
Ответ прост: 2 * 6 = 12.
Задача №2.
Есть 1 кубик, 2 шарика, 3 цветка и 4 конфеты. Сколькими способами можно вытянуть кубик, шарик, цветок и конфету?
Решение аналогично: 1 * 2 * 3 * 4 = 24.
Причем левую часть можно записать гораздо проще: 4!
! в данном случае является не знаком препинания, а факториалом. С помощью него можно вычислить более сложные варианты и решать трудные задачи (существуют разные формулы, но об этом позже).
Задача №3.
Сколько двузначных чисел можно составить из 2 цифр?
Задача №4.
Сколько десятизначных чисел можно составить из 10 цифр?
Правило суммы
Тоже является базовым правилом комбинаторики.
Если А можно выбрать n раз, а В — m раз, то А или В можно выбрать (n + m) раз.
Задача №5.
В коробке лежат 5 красных, 3 желтых, 7 зеленых, 9 черных карандашей. Сколько есть способов вытащить 1 любой карандаш?
Ответ: 5 + 3 + 7 + 9 = 24.
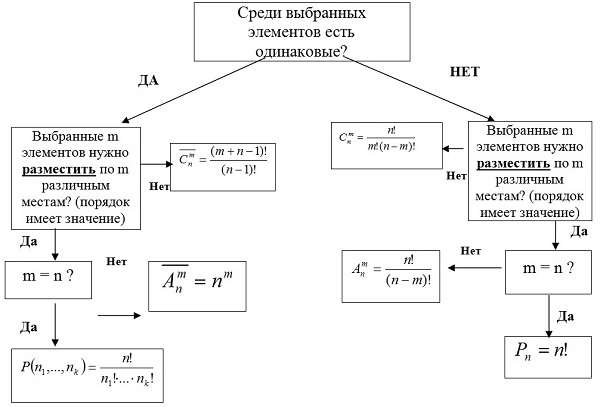
Сочетания с повторениями и без повторений
Под этим термином понимают комбинации в произвольном порядке из множества n по m элементов.
Число сочетаний равно количеству таких комбинаций.
Задача №6.
В коробке находится 4 разных фрукта. Сколькими способами можно достать одновременно 2 разных фрукта?
Где 4! – комбинация из 4 элементов.
С повторениями чуть сложней, комбинации считаются по такой формуле:
Задача №7.
Возьмем тот же самый случай, но при условии, что один фрукт возвращается в коробку.
Размещения с повторениями и без повторений
Под этим определением понимают набор m элементов из множества n элементов.
Задача №8.
Из 3 цифр надо выбрать 2, чтобы получались разные двузначные числа. Сколько вариантов?
А как же быть с повторениями? Здесь каждый элемент может размещаться несколько раз! В таком случае общая формула будет выглядеть следующим образом:
Задача №9.
Из 12 букв латинского алфавита и 10 цифр натурального ряда надо найти все варианты составления автомобильного кода региона.
Перестановки с повторениями и без повторений
Под этим термином понимают все возможные комбинации из n элементного множества.
Задача №10.
Сколько возможных пятизначных чисел можно составить из 5цифр? А шестизначных из 6 цифр? Семизначных из 7 цифр?
Решения, согласно вышеприведенной формуле, следующие:
А как же быть с повторениями? Если в таком множестве есть одинаковые по своей значимости элементы, то перестановок будет меньше!
Задача №11.
В коробке есть 3 одинаковых карандаша и одна ручка. Сколько перестановок можно сделать?
Ответ прост: 4! / (3! * 1!) = 4.
Комбинаторные задачи с решениями
Примеры всех возможных типов задач с решениями были даны выше. Здесь попробуем разобраться с более сложными случаями, встречающимися в нашей жизни.
| Типы задач | Что требуется найти | Методы решения |
| Магический квадрат | Фигура, в которой сумма чисел в рядах и столбцах должна быть одинакова (его разновидность – латинский квадрат). | Рекуррентные соотношения. Решается подобная же задача, но с гораздо меньшим множеством элементов по известным правилам и формулам. |
| Задача размещения | Стандартная производственная задача (например, в лоскутной технике) найти возможные способы разложения количества продуктов в ячейки в определенном порядке. | Включения и исключения. Как правило, применяется при доказательстве различных выражений. |
| Задачи про торговцев | Суть найти все возможные пути прохождения людей из пункта А в пункт В. | Траектории. Для этого вида задач характерно геометрическое построение возможных способов решения. |
Заключение
Стоит изучать эту науку, поскольку в век быстрой модернизации технологий потребуются специалисты, способные предоставить различные решения тех или иных практических задач.
КОМБИНАТОРИКА
Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены:
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m (

Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

Перестановки без повторений. Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
Что такое комбинаторные методы
1. Элементы комбинаторики.
2. Общие правила комбинаторики.
3. Генеральная совокупность без повторений и выборки без повторений.
4. Применение графов (схем) при решении комбинаторных задач.
1. Комбинаторика и ее возникновение.
Комбинаторика— это область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих данному множеству.
Комбинаторика возникла в XVI веке. В жизни привилегированных слоев тогдашнего общества большое место занимали азартные игры (карты, кости). Широко были распространены лотереи. Первоначально комбинаторные задачи касались в основном азартных игр: сколькими способами можно получить данное число очков, бросая 2 или 3 кости или сколькими способами можно получить 2-ух королей в некоторой карточной игре. Эти и другие проблемы азартных игр являлись движущей силой в развитии комбинаторики и далее в развитии теории вероятностей.
Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Тарталья. Он составил таблицы (числа способов выпадения k очков на r костях). Однако, он не учел, одна и та же сумма очков может выпасть различными способами, поэтому его таблицы содержали большое количество ошибок.
Теоретическое исследование вопросов комбинаторики предприняли в XVII веке французские математики Блез Паскаль и Ферма. Исходным пунктом их исследований были так же проблемы азартных игр.
Дальнейшее развитие комбинаторики связано с именами Я. Бернулли, Г. Лейбница, Л. Эйлера. Однако, и в их работах основную роль играли приложения к различным играм.
Сегодня комбинаторные методы используются для решения транспортных задач, в частности задач по составлению расписаний, для составления планов производства и реализации продукции и т.д.
2. Общие правила комбинаторики.
Правило суммы: Если некоторый объект А может быть выбран m способами, а объект В- k способами, то объект «либо А, либо В» можно выбрать m + k способами.
1. Допустим, что в ящике находится n разноцветных шаров. Произвольным образом вынимается 1 шарик. Сколькими способами это можно сделать?
Распределим эти n шариков по двум ящикам: в первый- m шариков, во второй- k шариков. Произвольным образом из произвольно выбранного ящика вынимается 1 шарик. Сколькими способами это можно сделать?
В морском семафоре каждой букве алфавита соответствует определенное положение относительно тела сигнальщика двух флажков. Сколько таких сигналов может быть?
Решение: Общее число складывается из положений, когда оба флажка расположены по разные стороны от тела сигнальщика и положений, когда они расположены по одну сторону от тела сигнальщика. При подсчете числа возможных положений применяется правило суммы.
Правило произведения: Если объект А можно выбрать m способами, а после каждого такого выбора другой объект В можно выбрать (независимо от выбора объекта А) k способами, то пары объектов «А и В» можно выбрать m *k способами.
1. Сколько двузначных чисел существует?
Решение: Число десятков может быть обозначено любой цифрой от 1 до 9. Число единиц может быть обозначено любой цифрой от 0 до 9. Если число десятков равно 1, то число единиц может быть любым (от 0 до 9). Таким образом, существует 10 двузначных чисел, с числом десятков- 1. Аналогично рассуждаем и для любого другого числа десятков. Тогда можно посчитать, что существует 9 *10 = 90 двузначных чисел.
2. Имеется 2 ящика. В одном лежит m разноцветных кубиков, а в другом- k разноцветных шариков. Сколькими способами можно выбрать пару «Кубик-шарик»?
3. Генеральная совокупность без повторений и выборки без повторений.
Пример: Набор из n разноцветных лоскутков.
Выборкой объема k ( k n ) называется группа из m элементов данной генеральной совокупности.
Размещениями из n элементов по k называются такие выборки, которые содержат по k элементов, выбранных из числа данных n элементов генеральной совокупности без повторений, и отличаются друг от друга либо составом элементов, либо порядком их расположения.
Преобразовав данную формулу, имеем:
Следует помнить, что 0!=1.
1. В первой группе класса А первенства по футболу участвует 17 команд. Разыгрываются медали: золото, серебро и бронза. Сколькими способами они могут быть разыграны?
Решение: Комбинации команд-победителей отличаются друг от друга составом и порядком следования элементов, т.е. являются размещениями из 17 по 3.
2. Научное общество состоит из 25-ти человек. Необходимо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами это можно сделать?
Решение: Комбинации руководящего состава общества отличаются друг от друга составом и порядком следования элементов, т.е. являются размещениями из 25 по 4.
1. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что они должны состоять из различных цифр?
Решение: Имеем перестановки из 5 элементов.
Сочетаниями без повторений из n элементов по k называются такие выборки, которые содержат по k элементов, выбранных из числа данных n элементов генеральной совокупности без повторений, и отличаются друг от друга только составом элементов.
— число сочетаний из n по k
Элементы каждого из сочетаний можно расставить способами. Тогда
1. Если в полуфинале первенства по шахматам участвует 20 человек, а в финал выходят лишь трое, то сколькими способам и можно определить эту тройку?
Решение: В данном случае порядок, в котором располагается эта тройка, не существенен. Поэтому тройки, вышедшие в финал, являются сочетаниями из 20 по 3.
Решение: В данном случае порядок, в котором располагается эта тройка, не существенен. Поэтому тройки делегатов являются сочетаниями из 10 по 3.
4. Применение графов (схем) при решении комбинаторных задач.
В случае, когда число возможных выборов на каждом шагу зависит от того, какие элементы были выбраны ранее, можно изобразить процесс составления комбинаций в виде «дерева». Сначала из одной точки проводят столько отрезков, сколько различных выборов можно сделать на первом шагу. Из конца каждого отрезка проводят столько отрезков, сколько можно сделать выборов на втором шагу, если на первом шагу был выбран данный элемент и т.д.
Составим соответствующее «дерево».
Ответ: 10 комбинаций.
Такое дерево является графом и применяется для решения комбинаторных задач.
Комбинаторное мышление
Логическое мышление, творческое мышление, аналитическое мышление – известные всем виды мышления. Однако, есть и такие, услышать о которых можно не часто. К их числу относится комбинаторное мышление, и в этой статье мы хотим поговорить именно о нем: рассмотрим само понятие, побеседуем на тему актуальности его развития (а о развитии мышления глобально вы можете узнать отсюда) и коротко коснемся комбинаторики – раздела математики, изучающего комбинаторные задачи.
Что такое комбинаторное мышление
Комбинаторным мышлением принято называть способность человека к решению комбинаторных задач. Интересен тот факт, что оно представляет собой как бы переходную форму от образного мышления к абстрактно-логическому, а также наоборот, т.к. оно включает в себя самые разные элементы: мотивационные, операционные, содержательные, абстрактно-логические и образные. Это, кстати, служит одной из причин, почему комбинаторное мышление тесно связано с логикой. Также обращаем ваше внимание на то, что данный тип мышления не может формироваться самостоятельно и для его развития необходимо прибегать к специальным педагогическим методикам.
Суть же комбинаторного мышления состоит в том, что при его активизации мозг человека занят поиском и преобразованием каких-либо одних элементов в другие, придавая им новые формы и комбинации. Вот лишь некоторые особенности этого процесса:
Ко всему прочему есть еще и разные типы комбинаторного мышления. Всего их три категории:
Обусловлено это разнообразие тем, что рассматриваемый вид мышления относится к самостоятельной форме интеллектуальной активности. В характеристику категорий мы углубляться не будем (при желании вы можете найти интересующую информацию самостоятельно), а лучше расскажем о том, почему комбинаторное мышление нужно развивать.
О развитии комбинаторного мышления
Актуальность развития комбинаторного мышления может быть рассмотрена с нескольких сторон, однако каждая из них так или иначе связана непосредственно с логикой:
Исходя из этого, переоценить важность развития комбинаторного мышления достаточно сложно, т.к. вместе с ним развивается и логика, и образное восприятие, и способность к поиску причинно-следственных связей, и мышление в целом и т.д. Хотя, если говорить о развитии мышления как такового, и не изобретать велосипед, мы советуем вам пройти наш курс по когнитивистике, а с комбинаторным мышлением разбираться в свободное время по желанию. Но если все-таки вам интересно узнать о нем больше, спешим познакомить вас с комбинаторикой.
Комбинаторика
В жизни каждого из нас время от времени бывают такие задачи, решить которые можно несколькими способами. И чтобы сделать это правильно, очень важно учесть все эти способы. Именно по этой причине нужно уметь перебирать все возможные варианты и устанавливать их количество. Как раз такие задачи и носят название комбинаторных, а их изучением занимается конкретный раздел математики – комбинаторика.
Заметим, что подобного рода задачи волновали людей с древнейших времен. Так, еще в Древнем Китае люди составляли магические квадраты, где конкретные числа по всем совпадениям всегда давали одну и ту же сумму. А древние греки занимались подсчетом числа комбинаций слов разной длины в стихотворных размерах, изучали теорию фигурных чисел, а также исследовали фигуры, которые могут получиться из элементов специальным способом разрезанного квадрата и т.д. Позже комбинаторные задачи стали появляться и в области игр, таких как кости, карты, домино, шахматы, шашки и т.п.
Сама комбинаторика возникла в 17 веке и изначально рассматривала комбинаторные задачи, касающиеся азартных игр. По мере их изучения вырабатывались общие методы решения задач и определялись формулы, позволяющие подсчитывать число комбинаций. Также появление комбинаторики тесно связано с теорией вероятности, для решения задач которой изначально было необходимо уметь вести подсчет количества различных комбинаций, подчиненных конкретным условиям. В 18 веке такие задачи изучались Г. Галилеем, Н. Тартальей, Д. Кардано, а позже – математиками П. Фермой, Б. Паскалем и другими. Множество достижений в представленной области принадлежит также Л. Эйлеру. Задачами из области комбинаторики были заинтересованы, кроме всех прочих, математики, составлявшие и разгадывавшие шифры и изучавшие древние письменности.
Сегодня же комбинаторика применятся с целью решения огромного количества теоретических и практических задач, где речь идет о возможных исходах, в том числе и благоприятных, для конкретных случаев. Применение она нашла и во всех научно-технических областях, включая биологию (посредством нее, например, исследуется состав ДНК и белков), химию, механику и другие области.
Интересно отметить, что с развитием комбинаторики было обнаружено, что, невзирая на визуальное различие вопросов, которые она изучает, большинство из них обладают одним и тем же математическим содержанием, результатом чего становятся задачи на тему множеств и их подмножеств. Со временем ученые определили ряд базовых видов задач, решение которых позволяет изучить многие комбинаторные проблемы. А одной из важнейших областей комбинаторики является теория перечислений – именно при помощи нее возможно определить количество решений разного рода комбинаторных задач. К слову добавим, что важность комбинаторики обусловлена и тем фактом, что с определением объектов и их расположением в каком-либо вообще порядке людям приходится сталкиваться, пожалуй, во всех сферах деятельности человека.
И в заключение еще несколько слов о связи комбинаторного мышления и математики.
Комбинаторное мышление и математика
Особое место решение задач комбинаторного характера занимает, как уже стало ясно, в математике, причем роль этого навыка становится все серьезнее. Причина же состоит в том, что такие задачи обладают огромным потенциалом для развития мышления вообще и для обучения решению проблем в обычной каждодневной жизни.
В начальных курсах математики данные задачи решаются в основном методом подбора, а чтобы сделать этот процесс проще нередко применяются графы и таблицы. Кроме того, включение комбинаторных задач в математические курсы сопряжено также и с тем, что повышается развивающая функция математики, ведь их решение предполагает симбиоз алгоритмического и эвристического стилей мышления. Эвристический элемент здесь нужен, чтобы адекватно воспринять задачу, найти ее решение, составить алгоритм перебора или определения компонентов, а алгоритмический элемент – для грамотного выполнения составленного алгоритма.
Таким образом, для обучения комбинаторному мышлению требуется не просто задействовать особые педагогические методы, но и обращаться к соответствующим образом подготовленным специалистам.
Надеемся, эта информация будет для вас полезной, но выводы делать, естественно, вам.