что такое коэффициент экстинкции

Коэффициент экстинкции

Содержание

Десятичный показатель ослабления

В дифференциальной форме его можно записать так:

Натуральный показатель ослабления

Его вид в дифференциальной форме таков:

Уравнения с участием натурального показателя ослабления имеют более компактный вид, чем в случае использования десятичного показателя поглощения, и не содержат имеющего искусственное происхождение множителя ln(10). Поэтому в научных исследованиях фундаментального характера чаще предпочитают использовать натуральный показатель ослабления.

Единицы измерения

В рамках Международной системы единиц (СИ) выбор единиц измерения определяется соображениями удобства и сложившимися традициями. Наиболее широко используются обратные сантиметры (см −1 ) и обратные метры (м −1 ).

После создания оптических материалов с экстремально низким потерями и последовавшего вслед за этим развитием волоконной оптики в качестве единицы измерения показателя ослабления стали использовать дБ/км (dB/km). В этом случае расчет значений показателя ослабления производится по формуле:

Об особенностях терминологии

Наличие близких по звучанию терминов приводит к широко распространенным неточностям и ошибкам в их употреблении и возникающим вследствие этого недоразумениям. Наиболее часто происходит смешение понятий в таких парах различных по смыслу терминов:

Ситуация усугубляется различиями в терминологии, используемой в русско- и англоязычной литературе. В частности, недоразумения происходят из-за того, что в русском языке эквивалентом для «Attenuation coefficient» является не созвучный ему «Коэффициент ослабления», а «Показатель ослабления». Аналогично, эквивалентом английского «Absorption coefficient» является не Коэффициент поглощения, а термин «Показатель поглощения».

Источник

Оптическая плотность (экстинкция)

По мере увеличения размеров частиц интенсивность рассеянного света перестает возрастать в зависимости от объема V частиц [см. формулу (8.2)], и рассеяние становится неравномерным.

Рассеяние света, схема которого приведена на рис. 8.1, б, отличается от рэлеевского и имеет место тогда, когда размеры частиц лежат в диапозоне

Особенности воздействия света на частицы относительно больших размеров обусловлены интерференцией отраженных и преломленных лучей на границе раздела между дисперсной фазой и дисперсионной средой. С учетом классификации частиц-дисперсной фазы по размерам (см. табл. 1.3) можно заключить, что условие (8.7) выполняется для грубодисперсных и отчасти для cреднедисперсных систем.

Условия (8.1), (8.6) и (8.7) определяют особенности воздействия света на частицы дисперсной фазы в зависимости от соотношения между длиной волны света и размерами частиц.

Оптические свойства дисперсных систем, способных к поглощению света, можно характеризовать по изменению интенсивности света, прошедшего через эту систему. Если интенсивность падающего света обозначить через J₀ (pиc. 8.2), а интенсивность рассеянного света — J_р, то J_пр будет характеризовать интенсивность прошедшего света. Интенсивность прошедшего света в отношении отдельных частиц определяется на основе закона Бугера — Ламберта:

где к — коэффициент поглощения; а — размер частиц дисперсной фазы.

Интенсивность прошедшего света можно представить как разности между интенсивностью падающего J₀ и поглощенного веществом J_пог света. Коэффициент поглощения можно рассматривать как величину, обратную расстоянию, на котором интенсивность света снижается в е раз, т.е. до 37% от первоначального значения J₀. Так, для 1%-го раствора некоторых полимеров это расстояние соответствует примерно 10 м.

Для оценки соотношения интенсивности прошедшего и падающего света можно воспользоваться уравнением (8.8), из которого следует:

Величину Д называют оптической плотностью или экстинкцией. Экстинкция характеризует ослабление луча света при его распространении в веществе. При рассмотрении отдельных частиц, когда соблюдается условие (8.7), экстинкция вызвана лишь поглощением света.

В отношении дисперсной системы экстинкция может отражать не только поглощение, но и рассеяние света. В этих условиях коэффициент к в уравнениях (8.8) и (8.9) отражает совокупное действие поглощения и рассеяния света. Иногда рассеянный свет рассматривают как фиктивно поглощенный и определяют суммарно поглощенный свет.

Коэффициент к зависит от массовой концентрации дисперсной фазы ν_м и может быть представлен следующим образом:

где к₁ — коэффициент пропорциональности, называемый мутностью.

Рис. 8.2. Взаимодействие света с дисперсной системой

Интенсивность рассеянного света, прошедшего через раствор определенной концентрации или через дисперсную систему, определяется законом Бугеpa — Ламберта — Бера, который, учитывая уравнения (8.8) и (8.10), можно записать так:

, (8.11)

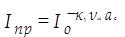
где а_c — толщина слоя дисперсной системы, вещества или раствора.

Если считать, что для дисперсной системы интенсивность поглощенного света равна интенсивности рассеянного (J_пр = J_пог), то учитывая уравнения (8.8)—(8.11), можно записать следующее выражение для экстинкции:

. (8.12)

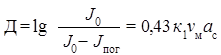
При помощи формулы (8.12) можно определить экстинкцию Д и кoэффициенты к и к₁ для дисперсных систем с учетом размеров их частиц и концентрации дисперсной фазы ν_м.

Таким образом, рассеяние света высокодисперсными системами определяется по закону Рэлея, а ослабление света дисперсными системами — по закону Бугера — Ламберта — Бера.

В реальных полидисперсных системах свойства частиц дисперсной фазы могут быть различны (например, часть частиц способна поглощать свет, а другая — рассеивать), поэтому оптические свойства таких систем будут определяться рассеянием, поглощением и отражением света, а также рядом других оптических явлений.

Источник

(1) — закон Бугера-Ламберта-Бэра (C – молярная концентрация, l – длина оптического пути, ε – молярный коэффициент поглощения, или молярный коэффициент экстинкции).

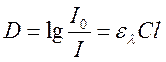
Если в образце присутствуют несколько компонентов, поглощающих в данной области, то оптическая плотность на данной длине волны определяется суммарным поглощением всех компонентов. Это создаёт некоторые трудности для идентификации спектров поглощения. Кроме того, появляются ограничение на использование растворителей. Его концентрация обычно в несколько тысяч раз превосходит концентрацию определяемого вещества, значит, если растворитель поглощает в данной области, то поглощение определяемого компонента может оказаться незаметным на фоне поглощения растворителя. Таким образом, к растворителю предъявляется требование полной прозрачности в данной спектральной области, т.е. .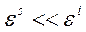

Молярный коэффициент экстинкции зависит от многих факторов. Их влияние может приводить к отклонениям от закона Бугера-Ламберта-Бэра.

Во-первых, 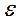зависит от интенсивности падающего излучения. С ростом интенсивности происходит изменение заселённости основного состояния, что приводит к уменьшению коэффициента экстинкции. Как правило, столь мощные источники излучения в спектроскопии не используются.

Во-вторых, значение 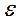сильно зависит от внешних параметров – температуры, давления и т.п. Рост температуры способствует уширению полосы поглощения за счёт увеличения заселённости колебательных уровней, отвечающих основному электронному состоянию.

В-третьих, величина молярного коэффициента поглощения определяется растворителем и составом раствора (в том числе и его ионной силой), так как электрохимическое взаимодействие с компонентами раствора или растворителем приводит к изменению вида спектра поглощения (смещение полосы поглощения, изменение интенсивности поглощения, появление или исчезновение полос поглощения). Поэтому иногда даже в очень разбавленных растворах наблюдается непостоянство молярного коэффициента экстинкции.

Наконец, величина 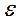зависит от инструментального оформления опыта. Эксперимент может давать абсолютное значение оптической плотности или же величину, измеренную относительно некоторого стандарта, в качестве которого может быть выбран, к примеру, чистый растворитель. Ясно, что в последнем случае измерения оказываются точнее, так как аннулируется влияние систематических ошибок измерения (например, учитывается ошибка, связанная с рассеянием излучения на частицах раствора). Тем не менее, остаются ошибки, связанные со схемой измерения: нарушение пропорциональности между интенсивностью падающего излучения и регистрируемым сигналом, частичное расхождение пучка света, некоторый диапазон длин волн, приводящий к отклонению от монохроматичности и т.д.

В связи с этим принято для каждого вещества проверять выполнимость закона Бугера-Ламберта-Бэра на опыте.

АНАЛИЗ СПЕКТРОВ МНОГОКОМПОНЕНТНЫХ СИСТЕМ

Анализ спектров смесей, как уже было сказано, представляет собой непростую задачу. Рассмотрим простейший пример. Пусть в растворе есть только 2 компонента – А и В. Растворитель выберем полностью прозрачным в данной области спектра. Кроме того, пусть частицы А и В различно поглощают в исследуемой области и способны к взаимопревращениям. Их концентрации связаны соотношением 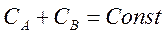. По спектру поглощения можно определить значения этих концентраций.

Возможны 2 ситуации: вещества имеют сильно отличающиеся спектры или вещества имеют сходные спектры.

В первом случае рабочую длину волны выбирают так, чтобы одно вещество не имело поглощения на данной длине волны, а другое поглощалось бы максимально. По известному значению суммарной концентрации и оптической плотности легко определить концентрации А и В.

В противном случае, в качестве рабочей длины волны выбирают значение, при котором отличие молярных коэффициентов экстинкции максимально. 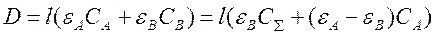(2). При некоторой длине волны молярные коэффициенты экстинкции обеих форм оказываются равны. Оптическая плотность при этой длине волны определяется только суммарной концентрацией частиц А и В и не зависит от их соотношения. Спектральные кривые растворов пересекаются в одной точке, называемой изобестической.

Точность анализа смеси может быть охарактеризована величиной 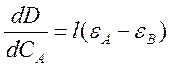. При заданной длине оптического пути (толщины кюветы с исследуемым веществом), чувствительность достигает максимума в точке, где разность молярных коэффициентов экстинкции максимальна.

ОПРЕДЕЛЕНИЕ СТЕПЕНИ ДИССОЦИАЦИИ СЛАБОЙ КИСЛОТЫ

Чтобы распечатать файл, скачайте его (в формате Word).

Источник