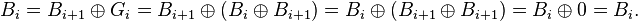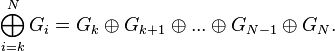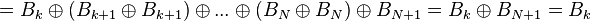что такое код грея
Код грея
Код Грея, рефлексный двоичный код — двоичная система нумерования, в которой два соседних значения различаются только в одном двоичном разряде.
Изначально предназначался для защиты от ложного срабатывания электромеханических переключателей. Сегодня коды Грея широко используются для упрощения выявления и исправления ошибок в системах связи, а также в формировании сигналов обратной связи в системах управления.
Содержание
Название
Название рефлексный (отражённый) двоичный код происходит от факта, что вторая половина значений в коде Грея эквивалентна первой половине, только в обратном порядке, за исключением старшего бита, который просто инвертируется. Если же разделить каждую половину ещё раз пополам, свойство будет сохраняться для каждой из половин половины и т. д.
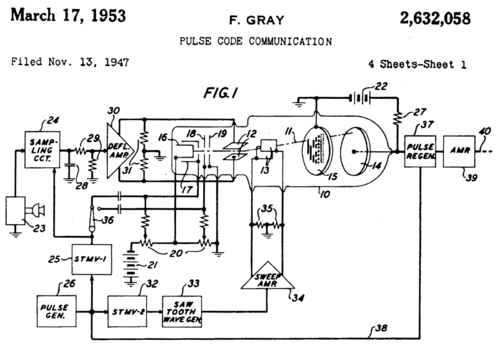
Код получил имя исследователя лабораторий Bell Labs Фрэнка Грея. Он использовал этот код в своей импульсной системе связи, для чего был написан патент за номером 2632058.
Применения
Использование кодов Грея основано прежде всего на том, что он минимизирует эффект ошибок при преобразовании аналоговых сигналов в цифровые (например, во многих видах датчиков).
Широко применяются коды Грея и в теории генетических алгоритмов [2] для кодирования генетических признаков, представленных целыми числами.
Алгоритмы преобразования
Ниже представлен один из алгоритмов создания последовательности кода Грея заданной глубины, записанный на языке
Алгоритм преобразования из двоичной системы счисления в код Грея, записанный на языке C:
обратный алгоритм (преобразование из кода Грея в двоичную систему счисления):
рекурсивная функция построение кода Грея на языке C:
См. также
Примечания
Библиография
Ссылки
Полезное
Смотреть что такое «Код грея» в других словарях:
код Грея — Циклический двоичный код. [http://www.morepc.ru/dict/] Тематики информационные технологии в целом EN Gray code … Справочник технического переводчика
Код Грея — 2 битный код Грея 00 01 11 10 3 битный код Грея 000 001 011 010 110 111 101 100 4 битный код Грея 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 Код Грея система счисления, в которой два соседних значения… … Википедия
код Грея — Gray kodas statusas T sritis automatika atitikmenys: angl. Gray code vok. Gray Code, m rus. код Грея, m pranc. code de Gray, m ryšiai: sinonimas – Grėjaus kodas … Automatikos terminų žodynas
код Грея — n мерная двоичная система в виде графа. Коды Грея задаются так, чтобы двоичные слова отличались на расстояние Хемминга, равное единице … Словарь лингвистических терминов Т.В. Жеребило
Код Джонсона — Код Джонсона двоичная система счисления, в которой два соседних значения различаются только в одном двоичном разряде. Принципы формирования кода Джонсона 1. Код Джонсона является кодом с избытком, то есть для числа разрядов больше 2 в коде… … Википедия
Код Грэя — 2 битный код Грея 00 01 11 10 3 битный код Грея 000 001 011 010 110 111 101 100 4 битный код Грея 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 Код Грея, рефлексный двоичный код двоичная система нумерования, в… … Википедия
Коды грея — 2 битный код Грея 00 01 11 10 3 битный код Грея 000 001 011 010 110 111 101 100 4 битный код Грея 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 Код Грея, рефлексный двоичный код двоичная система нумерования, в… … Википедия
Преобразователь угол-код — Датчик угла Датчик угла или преобразователь угол код, также называемый энкодер устройство, предназначенное для преобразования угла поворота вращающегося объекта (вала) в электрические сигналы, позволяющие определить угол его поворота. Широко… … Википедия
рефлексный код — код Грея циклический код — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы код Греяциклический код EN reflected code … Справочник технического переводчика
Ханойская башня — Модель Ханойской башни с восемью дисками Ханойская башня является одной из популярных головоломок XIX века. Даны три стержня, на один из которых нанизаны восемь колец, причем кольца отличаются … Википедия
Код Грея
Из Википедии — свободной энциклопедии
| Число | Бинарный код | Код Грея |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
Код Гре́я — двоичный код, иначе зеркальный код, он же код с отражением, в котором две «соседние» (в упорядоченном, то есть лексикографическом, наборе) кодовые комбинации различаются только цифрой в одном двоичном разряде. Иными словами, расстояние Хэмминга между соседними кодовыми комбинациями равно 1.
Наиболее часто на практике применяется рефлексивный двоичный код Грея, хотя в общем случае существует бесконечное множество кодов Грея со значениями цифр в разрядах, взятых из различных алфавитов. В большинстве случаев, под термином «код Грея» понимают именно рефлексивный бинарный код Грея.
Изначально предназначался для защиты от ложного срабатывания электромеханических переключателей. Сегодня коды Грея широко используются для упрощения выявления и исправления ошибок в системах связи, а также в формировании сигналов обратной связи в системах управления.
Про геометрический смысл кодов Грея
Коды Грея имеют близкую родственную связь с кривой Гильберта.
Впрочем, при общении с коллегами выяснилось, что эта несложная зависимость выглядит в их глазах как нечто нетривиальное. Поиск в интернетах навскидку ничего не дал кроме мутной фразы в вики: “кривые Гильберта в пространствах большей размерности являются представителями обобщений кодов Грея”. Поэтому возникло желание раскрыть тему — коротенько, простым языком.
В результате под катом — «скандалы, интриги, расследования».
Основная особенность кода Грея — два соседних в лексикографическом порядке значения отличаются только в одном разряде. С другой стороны, кривая Гильберта непрерывна — расстояние между двумя соседними точками всегда единица. Уже только одно это намекает об их внутренней связи.
Код Грея описывает похождения кривой Гильберта в рамках единичного гиперкуба. В самом деле, если взять 3-разрядный код и нарисовать его в 3-мерном пространстве (принимая каждый разряд за соответствующую координату), получим
Фиг.1 3-разрядный код Грея как 3-мерный куб
Знакомая картина — это 3-мерный симплекс кривой Гильберта! Последовательно заменяя каждый узел симплекса на такой же симплекс (с учетом поворотов и отражений для сохранения непрерывности), получим кривую Гильберта 4х4х4.
Продолжая эти итерации, сможем непрерывно заполнить кубическую решетку любого размера.

Фиг.2 несколько итераций симплекса кривой Гильберта.
Но как так получилось?
Известно, что код Грея самоподобен. Его иногда называют зеркальным “из-за того, что первая половина значений при изменении порядка эквивалентна второй половине, за исключением старшего бита. Старший бит просто инвертируется”. Для наглядности, 3-разрядный код — самый старший разряд — самый левый:
Раз уж речь зашла о самоподобии, начнём с начала — с одноразрядного кода. Строго говоря, можно было бы начать и с нулевой размерности — точки, принципиально это ничего не меняет, просто слов пришлось бы написать больше.
Одноразрядный код Грея даже проще, чем трёхлинейная винтовка, он либо 0, либо 1.
Геометрически это соответствует одномерному единичному кубу — отрезку. По отрезку можно двигаться либо из начала в конец, либо из конца в начало — с точностью до симметрии это одно и то же. Но всё же, началом будем называть то место, где значение меньше (вспомним, что стороны куба это разряды числа), а концом — где больше.

Фиг.3 Первые две итерации “миссионерского” варианта
Здесь красным цветом выделена предыдущая итерация, синим — её клон, бирюзовым — их соединение.
Обратим внимание — соединение всегда проходит по единственной размерности — вновь добавленной, отсюда в силу самоподобия и появляется основная особенность кода Грея. А раз соединяется конец предыдущей итерации с концом её клона, возникает “зеркальность” — при обходе, клон мы вынуждены проходить в обратном порядке. Вне зависимости от размерности. Здесь же видно происхождение и особенности кривой Гильберта — как бы ни была велика решетка (любой размерности), на низовом уровне это всё тот же единичный куб с переходами длиной в единицу.

Фиг.4 Первые две итерации варианта “паровозик”, те же цвета
А ведь и эта музыка нам знакома — получился симплекс Z-кривой. Слово симплекс здесь также означает, что если взять каждую его точку и заменить на симплекс, получим куб 4х4х4, продолжая итерации — можно заполнить сколь угодно большую кубическую решетку.
Забавно, что в этом случае преобразование пройденного от начала координат пути в код, который может быть разобран на разряды-координаты тривиально.
Тогда как случае кода Грея это G = W ^ (W >> 1), где W-пройденная длина, G — код Грея.

Фиг.5 первые две итерации Z-кривой (wiki)

Фиг.6 для сравнения, первые две итерации кривой Гильберта (wiki)
А ведь других то (естественных) вариантов обхода единичного гиперкуба и нет.
Вот и получается, что куда ни кинь, кругом Гильберт, Лебег … и пустота.
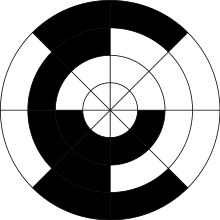
PS: на титульной картинке круговой энкодер с восьмиразрядным кодом Грея.
PPS: тут меня поправляют, что симплекс — вполне устоявшийся термин, нехорошо с ним так. Что-же, в данной статье ведь не просто симплекс, а симплекс кривой Гильберта или симплекс Z-кривой. Пусть правоверные математики меня простят.
Код Грея
Код Грея — система счисления, в которой два соседних значения различаются только в одном разряде. Наиболее часто на практике применяется рефлексивный двоичный код Грея, хотя в общем случае существует бесконечное множество кодов Грея для систем счисления с любым основанием. В большинстве случаев, под термином «код Грея» понимают именно рефлексивный бинарный код Грея.
Изначально предназначался для защиты от ложного срабатывания электромеханических переключателей. Сегодня коды Грея широко используются для упрощения выявления и исправления ошибок в системах связи, а также в формировании сигналов обратной связи в системах управления.
Содержание
Название
Название рефлексный (отражённый) двоичный код происходит от факта, что вторая половина значений в коде Грея эквивалентна первой половине, только в обратном порядке, за исключением старшего бита, который просто инвертируется. Если же разделить каждую половину ещё раз пополам, свойство будет сохраняться для каждой из половин половины и т. д.
Код получил имя исследователя лабораторий Bell Labs Фрэнка Грея. Он запатентовал и использовал этот код в своей импульсной системе связи (патент № 2632058).
Применения
Использование кодов Грея основано прежде всего на том, что он минимизирует эффект ошибок при преобразовании аналоговых сигналов в цифровые (например, во многих видах датчиков).
Коды Грея часто используются в датчиках-энкодерах. Их использование удобно тем, что два соседних значения шкалы сигнала отличаются только в одном разряде. Также они используются для кодирования номера дорожек в жёстких дисках.
Широко применяются коды Грея и в теории генетических алгоритмов [1] для кодирования генетических признаков, представленных целыми числами.
Код Грея используется для генерации сочетаний методом вращающейся двери [2]
В некоторых компьютерных играх (например, Duke Nukem 3D) для успешного прохождения уровня требуется подобрать нужную комбинацию положений нескольких переключателей. Для минимизации числа переключений при переборе вариантов следует использовать код Грея.
Алгоритмы преобразования
Преобразование двоичного кода в код Грея
Коды Грея легко получаются из двоичных чисел путём побитовой операции «Исключающее ИЛИ» с тем же числом, сдвинутым вправо на один бит. Следовательно, i-й бит кода Грея Gi выражается через биты двоичного кода Bi следующим образом:
где 
Ниже приведён алгоритм преобразования из двоичной системы счисления в код Грея, записанный на языке C:
Однако, необходимо помнить, что данный алгоритм будет работать правильно, если компилятор реализует циклический логический сдвиг (стандарт языка C не уточняет тип сдвига). Тот же самый алгоритм, записанный на языке Паскаль:
Пример: преобразовать двоичное число 10110 в код Грея.
Преобразование кода Грея в двоичный код
Обратный алгоритм – преобразование кода Грея в двоичный код – можно выразить рекуррентной формулой
причём преобразование осуществляется побитно, начиная со старших разрядов, и значение 
Однако приведённый алгоритм, связанный с манипуляцией отдельными битами, неудобен для программной реализации, поэтому на практике используют видоизменённый алгоритм:
где N – число битов в коде Грея (для увеличения быстродействия алгоритма в качестве N можно взять номер старшего ненулевого бита кода Грея); знак 
Действительно, подставив в формулу выражение для i-го бита кода Грея, получим

Здесь предполагается, что бит, выходящий за рамки разрядной сетки (
Ниже приведена функция на языке С, реализующая данный алгоритм. Она осуществляет последовательный сдвиг вправо и суммирование исходного двоичного числа, до тех пор, пока очередной сдвиг не обнулит слагаемое.
Тот же самый алгоритм, записанный на языке Паскаль:
Пример: преобразовать код Грея 11101 в двоичный код.
Быстрое преобразование 8/16/24/32-разрядного значения кода Грея в двоичный код на языке BlitzBasic:
Простой способ преобразования двоичного числа в код Грея выполняется по правилу: старший разряд записывается без изменения, каждый следующий символ кода Грея нужно инвертировать, если в натуральном коде перед этим была получена «1», и оставить без изменения, если в натуральном коде был получен «0».
Генерация кодов Грея
Код Грея для n бит может быть рекурсивно построен на основе кода для n–1 бит путём переворачивания списка бит (то есть записыванием кодов в обратном порядке), конкатенации исходного и перевёрнутого списков, дописывания нулей в начало каждого кода в исходном списке и единиц — в начало кодов в перевёрнутом списке. Так, для генерации списка для n = 3 бит на основании кодов для двух бит необходимо выполнить следующие шаги:
| Коды для n = 2 бит: | 00, 01, 11, 10 | |
| Перевёрнутый список кодов: | 10, 11, 01, 00 | |
| Объединённый список: | 00, 01, 11, 10 | 10, 11, 01, 00 |
| К начальному списку дописаны нули: | 000, 001, 011, 010 | 10, 11, 01, 00 |
| К перевёрнутому списку дописаны единицы: | 000, 001, 011, 010 | 110, 111, 101, 100 |
Ниже представлен один из алгоритмов создания последовательности кода Грея заданной глубины, записанный на языке Perl:
Рекурсивная функция построение кода Грея на языке C:
Быстрое преобразование 8/16/24/32-разрядного бинарного кода в код Грея на языке BlitzBasic:
См. также
Примечания
Библиография
Ссылки
Полезное
Смотреть что такое «Код Грея» в других словарях:
код Грея — Циклический двоичный код. [http://www.morepc.ru/dict/] Тематики информационные технологии в целом EN Gray code … Справочник технического переводчика
Код грея — 2 битный код Грея 00 01 11 10 3 битный код Грея 000 001 011 010 110 111 101 100 4 битный код Грея 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 Код Грея, рефлексный двоичный код двоичная система нумерования, в… … Википедия
код Грея — Gray kodas statusas T sritis automatika atitikmenys: angl. Gray code vok. Gray Code, m rus. код Грея, m pranc. code de Gray, m ryšiai: sinonimas – Grėjaus kodas … Automatikos terminų žodynas
код Грея — n мерная двоичная система в виде графа. Коды Грея задаются так, чтобы двоичные слова отличались на расстояние Хемминга, равное единице … Словарь лингвистических терминов Т.В. Жеребило
Код Джонсона — Код Джонсона двоичная система счисления, в которой два соседних значения различаются только в одном двоичном разряде. Принципы формирования кода Джонсона 1. Код Джонсона является кодом с избытком, то есть для числа разрядов больше 2 в коде… … Википедия
Код Грэя — 2 битный код Грея 00 01 11 10 3 битный код Грея 000 001 011 010 110 111 101 100 4 битный код Грея 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 Код Грея, рефлексный двоичный код двоичная система нумерования, в… … Википедия
Коды грея — 2 битный код Грея 00 01 11 10 3 битный код Грея 000 001 011 010 110 111 101 100 4 битный код Грея 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 Код Грея, рефлексный двоичный код двоичная система нумерования, в… … Википедия
Преобразователь угол-код — Датчик угла Датчик угла или преобразователь угол код, также называемый энкодер устройство, предназначенное для преобразования угла поворота вращающегося объекта (вала) в электрические сигналы, позволяющие определить угол его поворота. Широко… … Википедия
рефлексный код — код Грея циклический код — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы код Греяциклический код EN reflected code … Справочник технического переводчика
Ханойская башня — Модель Ханойской башни с восемью дисками Ханойская башня является одной из популярных головоломок XIX века. Даны три стержня, на один из которых нанизаны восемь колец, причем кольца отличаются … Википедия
Что такое код грея
Код Грея — система счисления, в которой два соседних значения различаются только в одном разряде. Наиболее часто на практике применяется рефлексивныйдвоичный код Грея, хотя в общем случае существует бесконечное множество кодов Грея для систем счисления с любым основанием. В большинстве случаев, под термином «код Грея» понимают именно рефлексивный бинарный код Грея.
Изначально предназначался для защиты от ложного срабатывания электромеханических переключателей. Сегодня коды Грея широко используются для упрощения выявления и исправления ошибок в системах связи, а также в формировании сигналов обратной связи в системах управления.
Содержание
[править] Название
Название рефлексный (отражённый) двоичный код происходит от факта, что вторая половина значений в коде Грея эквивалентна первой половине, только в обратном порядке, за исключением старшего бита, который просто инвертируется. Если же разделить каждую половину ещё раз пополам, свойство будет сохраняться для каждой из половин половины и т. д.
Код получил имя исследователя лабораторий Bell Labs Фрэнка Грея. Он запатентовал и использовал этот код в своей импульсной системе связи (патент № 2632058).
[править] Применения
Использование кодов Грея основано прежде всего на том, что он минимизирует эффект ошибок при преобразовании аналоговых сигналов в цифровые (например, во многих видах датчиков).
Коды Грея часто используются в датчиках-энкодерах. Их использование удобно тем, что два соседних значения шкалы сигнала отличаются только в одном разряде. Также они используются для кодирования номера дорожек в жёстких дисках.
Широко применяются коды Грея и в теории генетических алгоритмов [1] для кодирования генетических признаков, представленных целыми числами.
[править] Алгоритмы преобразования
[править] Преобразование двоичного кода в код Грея
Коды Грея легко получаются из двоичных чисел путём побитовой операции «Исключающее ИЛИ» с тем же числом, сдвинутым вправо на один бит. Следовательно, i-й бит кода Грея G i выражается через биты двоичного кода B i следующим образом:
где 
Ниже приведён алгоритм преобразования из двоичной системы счисления в код Грея, записанный на языке C:
Однако, необходимо помнить, что данный алгоритм будет работать правильно, если компилятор реализует циклический логический сдвиг (стандарт языка C не уточняет тип сдвига). Тот же самый алгоритм, записанный на языке Паскаль:
Пример: преобразовать двоичное число 10110 в код Грея.
[править] Преобразование кода Грея в двоичный код
Обратный алгоритм – преобразование кода Грея в двоичный код – можно выразить рекуррентной формулой
причём преобразование осуществляется побитно, начиная со старших разрядов, и значение 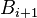
Однако приведённый алгоритм, связанный с манипуляцией отдельными битами, неудобен для программной реализации, поэтому на практике используют видоизменённый алгоритм:
где N – число битов в коде Грея (для увеличения быстродействия алгоритма в качестве N можно взять номер старшего ненулевого бита кода Грея); знак 
Действительно, подставив в формулу выражение для i-го бита кода Грея, получим

Здесь предполагается, что бит, выходящий за рамки разрядной сетки (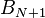
Ниже приведена функция на языке С, реализующая данный алгоритм. Она осуществляет последовательный сдвиг вправо и суммирование исходного двоичного числа, до тех пор, пока очередной сдвиг не обнулит слагаемое.
Тот же самый алгоритм, записанный на языке Паскаль:
Пример: преобразовать код Грея 11101 в двоичный код.
Быстрое преобразование 8/16/24/32-разрядного значения кода Грея в двоичный код на языке BlitzBasic:
Простой способ преобразования двоичного числа в код Грея выполняется по правилу: старший разряд записывается без изменения, каждый следующий символ кода Грея нужно инвертировать, если в натуральном коде перед этим была получена «1», и оставить без изменения, если в натуральном коде был получен «0».
[править] Генерация кодов Грея
Код Грея для n бит может быть рекурсивно построен на основе кода для n–1 бит путём переворачивания списка бит (то есть записыванием кодов в обратном порядке), конкатенации исходного и перевёрнутого списков, дописывания нулей в начало каждого кода в исходном списке и единиц — в начало кодов в перевёрнутом списке. Так, для генерации списка для n = 3 бит на основании кодов для двух бит необходимо выполнить следующие шаги:
| Коды для n = 2 бит: | 00, 01, 11, 10 | |
| Перевёрнутый список кодов: | 10, 11, 01, 00 | |
| Объединённый список: | 00, 01, 11, 10 | 10, 11, 01, 00 |
| К начальному списку дописаны нули: | 000, 001, 011, 010 | 10, 11, 01, 00 |
| К перевёрнутому списку дописаны единицы: | 000, 001, 011, 010 | 110, 111, 101, 100 |
Ниже представлен один из алгоритмов создания последовательности кода Грея заданной глубины, записанный на языке Perl:
Рекурсивная функция построение кода Грея на языке C:
Быстрое преобразование 8/16/24/32-разрядного бинарного кода в код Грея на языке BlitzBasic: