что такое изометрия в математике

Изометрия (математика)

Изоме́три́я, или движе́ние, или (реже) наложе́ние — биекция (преобразование), которая сохраняет расстояние между соответствующими точками, то есть если и — образы точек и , то .

Термин «изометрия» более распространён в метрической геометрии, в частности, в римановой геометрии. В общем случае метрического пространства (например, для неплоского риманова многообразия) движения могут существовать далеко не всегда.

Термин «движение» более распространён в евклидовой геометрии и смежных областях.

В евклидовом (или псевдоевклидовом) пространстве изометрия автоматически сохраняет также углы, то есть, сохраняются все скалярные произведения.

В этой статье ниже подразумевается евклидово пространство,

Содержание

Виды изометрии

На плоскости

В трёхмерном пространстве

В n-мерном пространстве

В -мерном пространстве движения сводятся ко всем ортогональным преобразованиям, параллельным переносам и композициям того и другого.

В свою очередь ортогональные преобразования могут быть представлены как композиции (собственных) вращений и зеркальных отражений.

Общие свойства изометрии

Движения как композиции симметрий

Любую изометрию в -мерном евклидовом пространстве можно представить в виде композиции не более чем отражений.

Так, параллельный перенос и поворот — композиции двух отражений, скользящее отражение и зеркальный поворот — трёх, винтовое наложение — четырёх.

Полезное

Смотреть что такое «Изометрия (математика)» в других словарях:

Изометрия — Изометрическая проекция аксонометрическая проекция, при которой длины единичных отрезков на всех трёх осях одинаковы. Применяется в машиностроительном черчении для отображения внешнего вида детали, а также в компьютерных играх. Изометрия… … Википедия

Хиральность (математика) — У этого термина существуют и другие значения, см. Хиральность (значения). В геометрии фигуру называют хиральной (и говорят, что она обладает хиральностью), если она не совпадает со своим зеркальным отображением, точнее, не может быть совмещена с… … Википедия

Вращение — У этого термина существуют и другие значения, см. Вращение (значения). Вращение сферы вокруг оси. Вращение круговое движение объекта. В плоском пространстве объект вращается вокруг центра (или точки) вращения. В трёхмерном пространстве объект… … Википедия

Абсолютная оптическая система — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей … Википедия

Идеальная оптическая система — Абсолютная оптическая система оптическая система, формирующая стигматическое изображение трехмерной области. Для формирования стигматического изображения необходимо, чтобы испущенные каждой точкой оптического объекта лучи после прохождения через… … Википедия

Изометричные поверхности — Изометричные поверхности поверхности в евклидовом или римановом пространстве такие, что между ними можно установить взаимно однозначное точечное соответствие, при котором каждая спрямляемая кривая одной из поверхностей имеет своим образом… … Википедия

ДИСКРЕТНАЯ ГРУППА — преобразований группа Г гомеоморфизмов хаусдорфова топологич. пространства X, удовлетворяющая следующему условию: для любых точек х, найдутся такие их окрестно сти U, V соответственно, что множество конечно. Стабилизатор точки относительно Д. г.… … Математическая энциклопедия

Движение — Содержание 1 Физика 2 Философия 3 Биология … Википедия

Источник

В математика, изометрия (или же соответствие, или же конгруэнтное преобразование) это расстояние-сохраняющее преобразование между метрические пространства, обычно считается биективный. [1]

Содержание

Вступление

Изометрии часто используются в конструкциях, где одно пространство встроенный в другом пространстве. Например, завершение метрического пространства M включает изометрию из M в M ‘, а набор частных пространства Последовательности Коши на M. Оригинальное пространство M таким образом изометрически изоморфный в подпространство полное метрическое пространство, и его обычно отождествляют с этим подпространством. Другие конструкции вложения показывают, что каждое метрическое пространство изометрически изоморфно закрытое подмножество некоторых нормированное векторное пространство и что каждое полное метрическое пространство изометрически изоморфно замкнутому подмножеству некоторого Банахово пространство.

Изометрический сюръективный линейный оператор на Гильбертово пространство называется унитарный оператор.

Определение изометрии

Позволять Икс и Y быть метрические пространства с метриками d_Икс и d_Y. А карта ж : Икс → Y называется изометрия или же сохранение расстояния если для любого а,б ∈ Икс надо

Изометрия выполняется автоматически инъективный; [1] в противном случае две разные точки, а и б, можно было бы отобразить в одну и ту же точку, что противоречит аксиоме совпадения метрики d. Это доказательство аналогично доказательству того, что заказать встраивание между частично упорядоченные наборы инъективно. Ясно, что любая изометрия между метрическими пространствами является топологическим вложением.

А глобальная изометрия, изометрический изоморфизм или же сопоставление это биективный изометрия. Как и любая другая биекция, глобальная изометрия имеет обратная функция. Обратное к глобальной изометрии также является глобальной изометрией.

Два метрических пространства Икс и Y называются изометрический если существует биективная изометрия из Икс к Y. В набор биективных изометрий из метрического пространства в себя образует группа относительно функциональная композиция, называется группа изометрии.

Есть также более слабое понятие изометрия пути или же дуговая изометрия:

А изометрия пути или же дуговая изометрия карта, сохраняющая длины кривых; такое отображение не обязательно является изометрией в смысле сохранения расстояния, и оно не обязательно должно быть биективным или даже инъективным. Этот термин часто сокращают до просто изометрия, поэтому следует позаботиться о том, чтобы определить из контекста, какой тип предназначен.

Изометрии между нормированными пространствами

Следующая теорема принадлежит Мазуру и Уламу.

Линейная изометрия

В внутреннее пространство продукта, приведенное выше определение сводится к

Посредством Теорема Мазура – ​​Улама, любая изометрия нормированных векторных пространств над р является аффинный.

Коллекторы

Определение

Характеристики

В Теорема Майерса – Стинрода. утверждает, что любая изометрия между двумя связными римановыми многообразиями является гладкой (дифференцируемой). Вторая форма этой теоремы утверждает, что группа изометрий риманова многообразия является Группа Ли.

Римановы многообразия которые имеют изометрии, определенные в каждой точке, называются симметричные пространства.

Обобщения

Смотрите также

Рекомендации

3.11 Любые два конгруэнтных треугольника связаны единственной изометрией.

Источник

Изометрия

Изометрия — это разновидность аксонометрической проекции, при которой в отображении трёхмерного объекта на плоскость коэффициент искажения (отношение длины спроецированного на плоскость отрезка, параллельного координатной оси, к действительной длине отрезка) по всем трём осям один и тот же. Слово «изометрическая» в названии проекции пришло из греческого языка и означает «равный размер», отражая тот факт, что в этой проекции масштабы по всем осям равны. В других видах проекций это не так.

Содержание:

Понятие геометрического преобразования

Преобразования фигур изучаются в курсе геометрии на плоскости и в пространстве. Если каждую точку данной фигуры на плоскости или в пространстве сместить каким-нибудь образом, то получим новую фигуру. Говорят, что эта фигура получена преобразованием из данной.

Вспомните определение числовой функции в курсе алгебры (см. с. 111). В геометрии также есть некоторые функции, заданные на множестве точек. Такие «геометрические функции» называют геометрическими преобразованиями.

Определение. Пусть преобразование фигуры F в фигуру переводит различные точки фигуры F в различные точки фигуры . Пусть произвольная точка X фигуры F при этом преобразовании переходит в точку фигуры . Преобразование фигуры в фигуру F, при котором точка перейдет в точку X, называют преобразованием, обратным данному.

В геометрии выделяют геометрические преобразования, сохраняющие расстояния между соответствующими точками. Такие геометрические преобразования называют изометриями (движениями).

Заметим, что есть геометрические преобразования, для которых не выполняется это свойство (например, надувая мыльный пузырь, мы тоже осуществляем геометрическое преобразование, но при этом изменяются расстояния между соответствующими точками).

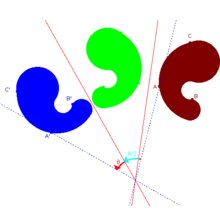
Поворот вокруг точки на данный угол

Если луч АС (рис. 2.399) поворачивать вокруг точки А против часовой стрелки, например, до положения АВ, то его последовательные положения «заметут» угол со сторонами АС и АВ.

Описанный выше процесс в геометрии называется поворотом луча на некоторый угол вокруг данной точки.

На плоскости вокруг точки можно поворачивать любую фигуру. На рисунке 2.400 изображен поворот «плоского» Буратино на углы 50° и 110° вокруг некоторой точки О.

На рис. 2.401 изображен поворот на угол 50° вокруг данной точки О. При этом перешел в . Видно, что равен .

Угол поворота, т. е. угол, на который мы поворачивали фигуру, всегда заключается в интервале от 0 до 180°: . При повороте на 0° все точки фигуры остаются на месте. Такой поворот на 0° только один.

Поворотов существует два: по часовой стрелке и против часовой стрелки. Так будет при любом заданном угле поворота. На рисунке 2.401 треугольник ABC повернули на угол в 50° вокруг точки о по часовой стрелке.

Определение. Поворотом фигуры Ф вокруг точки О на угол называют такое преобразование, при котором:

1) точка О переходит сама в себя (остается на месте);

2) любая точка Х фигуры Ф переходит в такую точку фигуры что всегда равен ;

3)

Существуют фигуры, которые при некоторых поворотах переходят сами в себя.

Про такие фигуры можно сказать, что они имеют центр поворота. При этом разные фигуры могут иметь разные углы поворота (при повороте на который фигура переходит сама в себя).

На рисунке 2.402 изображены фигуры, имеющие центр поворота.

Можно доказать следующую теорему.

Теорема 1. Поворот фигуры вокруг точки на данный угол есть изометрия.

Вращение фигуры вокруг оси на данный угол

На практике широко используется не поворот фигур на плоскости, а вращение фигуры вокруг оси в пространстве.

Определение. Вращением вокруг оси на угол называется такое преобразование пространства, при котором в каждой плоскости, перпендикулярной оси , происходит поворот на угол вокруг точки пересечения этой плоскости с осью.

Прямую называют осью вращения, угол — углом вращения.

Неподвижными элементами вращения являются точки оси вращения, а также все плоскости, перпендикулярные этой оси. Если то вращение можно считать тождественным преобразованием.

Существуют фигуры, имеющие ось вращения, т. е. такие фигуры, которые при вращении вокруг этой оси на соответствующие углы переходят сами в себя. Оси вращения имеют прежде всего круглые фигуры — сфера, шар, цилиндр, конус (рис. 2.403). В связи с этим их называют телами вращения.

Оси вращения имеют и различные многогранники, например куб и тетраэдр.

Можно доказать, что вращение фигуры вокруг оси является изометрией.

Симметрия относительно точки (центральная симметрия)

Определение. Пусть О — фиксированная точка и X — произвольная точка. Точку называют симметричной точке X относительно точки О, если точки X, О, лежат на одной прямой и ОХ = . Точка, симметричная точке О, есть сама точка О.

На рисунке 2.404 точки А и симметричны друг другу относительно точки О.

Определение. Пусть F — данная фигура и О — фиксированная точка. Преобразование фигуры F в фигуру при котором каждая ее точка X переходит в точку , симметричную X относительно данной точки О, называют преобразованием симметрии относительно точки О.

На рисунке 2.405 изображены две симметричные относительно точки О треугольные пирамиды.

Теорема 2. Центральная симметрия является изометрией.

Определение. Если преобразование симметрии относительно точки О переводит фигуру в себя, то фигуру называют центрально-симметричной, а точку О — ее центром симметрии.

Например, параллелограмм является центрально-симметричной фигурой. Центром его симметрии является точка пересечения диагоналей (рис. 2.406). Окружность с центром О тоже центрально-симметричная фигура с центром симметрии О (рис. 2.407). Все перечисленные фигуры плоские.

В пространстве, так же как и на плоскости, много примеров центрально-симметричных фигур. Например, на рисунках 2.408 и 2.409 изображены такие фигуры: это куб и параллелепипед.

Симметрия относительно прямой (осевая симметрия)

Определение. Пусть — фиксированная прямая. Точку называют симметричной точке X относительно прямой , если прямая перпендикулярна прямой и где О — точка пересечения прямых и . Если точка X лежит на прямой , то симметричная ей точка есть сама точка X, т. е. точка, симметричная точке , есть точка X.

На рисунке 2.410 точки симметричны относительно прямой

Определение. Преобразование фигуры F в при котором каждая точка X переходит в точку , симметричную относительно прямой , называют преобразованием симметрии относительно прямой . При этом фигуры называют симметричными относительно прямой .

На рисунке 2.411 изображены окружности, симметричные относительно прямой .

На рисунке 2.412 изображены две сферы, симметричные относительно прямой .

Осевая симметрия является изометрией.

Определение. Если преобразование симметрии относительно прямой переводит фигуру F в себя, то фигуру называют симметричной относительно прямой , а прямую называют осью симметрии фигуры.

Например, прямые, проходящие через точку пересечения диагоналей прямоугольника параллельно его сторонам, являются осями симметрии прямоугольника (рис. 2.413). Прямые, на которых лежат диагонали ромба, являются его осями симметрии (рис. 2.414).

Окружность симметрична относительно любой прямой, проходящей через ее центр (рис. 2.415).

В пространстве, как и на плоскости, много примеров фигур, имеющих оси симметрии. На рисунке 2.416 изображены такие фигуры: это прямоугольный параллелепипед, конус, правильная четырехугольная пирамида.

Симметрия относительно плоскости (зеркальная симметрия)

Определение. Пусть — произвольная фиксированная плоскость. Из точки X опускают перпендикуляр на плоскость (О — точка пересечения его с плоскостью ) и на его продолжении за точку О откладывают отрезок равный ОХ. Точки X и называют симметричными относительно плоскости (рис. 2.417).

Определение. Преобразование фигуры F в , при котором каждая точка X фигуры F переходит в точку , симметричную X относительно плоскости , называют преобразованием симметрии относительно плоскости . При этом фигуры F и называют симметричными относительно плоскости .

На рисунке 2.418 изображены две сферы, симметричные относительно плоскости .

Можно доказать такую теорему.

Теорема 3. Симметрия относительно плоскости является изометрией.

Кроме фигур, симметричных относительно некоторой плоскости, имеются фигуры, имеющие плоскость или плоскости симметрии.

Определение. Если преобразование симметрии относительно плоскости переводит фигуру в себя, то фигуру называют симметричной относительно плоскости , а плоскость называют плоскостью симметрии.

На рисунке 2.419 изображены две плоскости симметрии сферы. Заметим, что у сферы таких плоскостей симметрии бесконечное множество. У куба также имеются плоскости симметрии. На рисунке 2.420 изображены две из них.

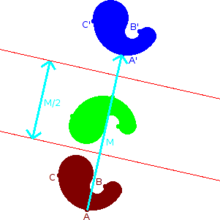
Параллельный перенос

Па рисунке 2.421 изображен параллельный перенос (сдвиг) некоторой произвольной фигуры F. Она перешла в фигуру . При этом точка А перешла в точку , точка В — в точку , точка С — в точку . Для удобства процесс перехода точек часто изображается отрезками со стрелками, которые называют направленными отрезками.

Можно сформулировать точное определение параллельного переноса.

Определение. Если каждую точку фигуры Ф перевести (сместить) в одном направлении (по сонап-равленным лучам) на одно и то же расстояние, то получим фигуру . Полученное в результате преобразование называют параллельным переносом.

Параллельные переносы обозначают буквой Т. Запись Т(А) = В читается: параллельный перенос Т переводит точку А в точку В.

Рассматривая, например, различные призмы, можно увидеть, что основания призмы могут быть совмещены друг с другом параллельным переносом.

На рисунке 2.422 основание призмы перейдет в пятиугольник , а произвольная точка X нижнего основания перейдет в точку X’ верхнего основания при параллельном переносе в направлении луча XX’.

Можно доказать теоремы 4 и 5.

Теорема 4. Параллельный перенос является изометрией.

Теорема 5. Отрезки двух параллельных прямых, заключенные между двумя другими параллельными прямыми, равны.

На рисунке 2.423 изображены две параллельные прямые и два параллельных отрезка АВ и CD. Согласно теореме 5, АВ = CD.

Определение и свойства изометрии

Определение. Преобразование фигуры F в фигуру называют изометрией, если оно сохраняет расстояние между соответствующими точками, т. е. переводит любые две точки А и В фигуры F в точки фигуры так, что

Все рассмотренные выше примеры геометрических преобразований являются изометриями.

Можно сформулировать и доказать некоторые общие свойства изометрии.

Теорема 6. При изометрии точки, лежащие на прямой, переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.

Из теоремы 6 следует, что при изометрии прямые переходят в прямые, полупрямые — в полупрямые, отрезки — в отрезки.

При изометрии сохраняются углы между полупрямыми. При изометрии плоскость переходит в плоскость.

Изометрии, выполненные последовательно, дают снова изометрию. Результат выполнения этих изометрий называют композицией изометрий.

На рисунке 2.424 изображено последовательное выполнение двух изометрий, фигура получена из фигуры F симметрией относительно оси р, а фигура получена из фигуры симметрией относительно точки О, в результате последовательного выполнения этих изометрий сохранились расстояния между соответствующими точками, а значит, фигура получена из фигуры F изометрией.

Теорема 7. Композиция двух вращений с одной и той же осью есть вращение.

Пример 1.

Даны две концентрические окружности. Постройте ромб, отличный от квадрата, так, чтобы: А) две вершины его принадлежали одной окружности, а две оставшиеся — другой; В) три вершины принадлежали одной окружности, а одна — другой.

Решение:

А) 1. Построим любой диаметр АВ одной окружности и перпендикулярный ему диаметр CD другой окружности (рис. 2.425).

2. Диагонали полученного четырехугольника CBDA в точке пересечения делятся пополам, значит, CBDA — параллелограмм.

3. Из симметрии отрезков АС и ВС относительно оси CD следует равенство сторон параллелограмма, т. е. CBDA — ромб.

В) 1. Диаметр АВ меньшей окружности продолжим до пересечения в точке С с большей окружностью.

2. Построим оси симметрии отрезков АС и ВС (рис. 2.426).

3. Мы получим два ромба, удовлетворяющие условию задачи:

Аналогично можно в первом случае построить еще один ромб, а во втором — еще два.

Пример 2.

Даны плоскость и две точки А и В вне ее. Найдите на плоскости такую точку N, чтобы сумма ее расстояний от А и В, т. е. AN + NB, была наименьшей.

Решение:

Если точки А и В расположены по разные стороны от плоскости , то очевидно, что искомая точка N — точка пересечения прямой АВ с плоскостью (рис. 2.427).

Если же точки А и В расположены по одну сторону от плоскости (рис. 2.428), то искомая точка N получится при пересечении прямой с плоскостью , где — точка, симметричная точке А относительно плоскости .

1. Докажем, что точка N искомая.

2. N находится на прямой , которая перпендикулярна отрезку и проходит через его середину ().

3. AN = , отсюда AN + NB = + NB.

4. Возьмем на плоскости произвольную точку К, отличную от N.

5. Соединив точки и К, получим отрезок , перпендикулярный отрезку и проходящий через его середину .

6. АК = .

7. АК + KB = + КВ.

8. Из имеем, что (7, неравенство треугольника).

9. Так как то ясно, что

10. Таким образом, приходим к выводу, что сумма AN + NB имеет наименьшее значение, и, следовательно, N — искомая точка.

Изометрия и равенство фигур

Используя понятия изометрии, можно дать еще одно определение равных фигур.

Определение. Фигуры F и называют равными, если они изометрией переводятся одна в другую.

Для обозначения равенства фигур употребляется знак равенства. Запись F = означает, что фигура F равна .

На рисунке 2.429 шары симметричны относительно плоскости, а значит, они равны.

На рисунке 2.430 кубы симметричны относительно точки, а значит, они равны.

На рисунке 2.431 треугольники равны, так как все они получены один из другого в результате изометрии.

Пример:

На рисунках 2.432 и 2.433 изображены два равных треугольника ABC и . Докажите, что эти треугольники совмещаются изомет-рией (или композицией изометрий), причем вершина А переходит в вершину

Решение:

Решение задачи зависит от расположения данных треугольников.

А) На рисунке 2.432 изображены два равных треугольника. Возможны такие построения:

1. получен из при симметрии относительно серединного перпендикуляра к отрезку .

2. получен из при симметрии относительно прямой, соединяющей точку с серединой отрезка

3. Последовательное выполнение изометрией есть изометрия. Таким образом, получен из изометрией — композицией дух осевых симметрий.

В) На рисунке 4.433 изображен другой вариант. получен из параллельным переносом в направлении, заданном лучом , на расстояние . Далее, получен из поворотом на угол а против часовой стрелки. Вывод аналогичен первому случаю.

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Источник