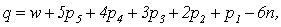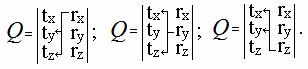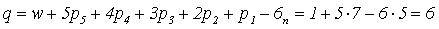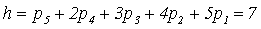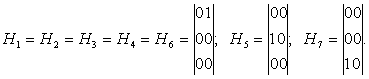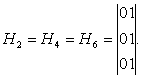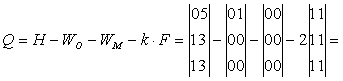что такое избыточные связи
Что такое избыточные связи
Кинематические пары (КП) классифицируются по следующим признакам:
Классификация КП по числу подвижностей и по числу связей приведена в таблице 2.1.
Классификация кинематических пар по числу связей и по подвижности.
| Класс пары | Число связей | Подвижность | Пространственная схема (пример) | Условные обозначения |
| I | 1 | 5 | ||
| II | 2 | 4 | ||
| III | 3 | 3 | ||
| IV | 4 | 2 | ||
| V | 5 | 2 |
Примечание: Стрелки у координатных осей показывают возможные угловые и линейные относительные перемещения звеньев. Если стрелка перечеркнута, то данное движение в КП запрещено (т.е. на данное относительное движение наложена связь).
Понятие о структурном синтезе и анализе.
Основные понятия структурного синтеза и анализа.
Основные структурные формулы.
Для расчета избыточных связей, согласно второму определению, используется следующая зависимость:
Пример структурного анализа механизма.
Функциональная схема на уровне типовых механизмов.
т. е. как пространственный данный механизм не имеет подвижности, так как число связей в нем существенно (на пять) превышает суммарную подвижность всех его звеньев. Однако от рассмотренного ранее плоского варианта пространственный механизм ничем не отличается, то есть он имеет две подвижности основную и местную. Как отмечено, выше связи, не изменяющие подвижности механизма, являются пассивными или избыточными. Для нашего механизма чилсло избыточных связей:
Структурная классификация механизмов по Ассуру Л.В.
Для решения задач синтеза и анализа сложных рычажных механизмов профессором Петербургского университета Ассуром Л.В. была предложена оригинальная структурная классификация. По этой классификации механизмы не имеющие избыточных связей и местных подвижностей состоят из первичных механизмов и структурных групп Ассура (см. рис. 2.6).
Под первичным механизмом понимают механизм, состоящий из двух звеньев (одно из которых неподвижное) образующих кинематическую пару с одной W пм =1 или несколькими W пм = 1 подвижностями. Примеры первичных механизмов даны на рис. 2.7.
Структурной группой Ассура (или гуппой нулевой подвижности) называется кинематическая цепь, образованная только подвижными звеньями механизма, подвижность которой (на плоскости и в пространстве) равна нулю ( W гр = 0).
| Класс и порядок по Ассуру | 1 кл. 2 пор. | 1 кл. 3 пор. | |
| Число звеньев группы n гр | 2 | 4 | и т. д. |
| Число кинематических пар p 1 | 3 | 6 | |
| Класс и порядок по Артоболевскому | 2 кл. 2 пор. | 3 кл. 3 пор. |
Дальнейшее развитие эта структурная классификация получила в работе [6], где была распространена на механизмы с высшими кинематическими парами.
| группа звеньев 5-6 |
| группа звеньев 3-4 |
| группа звеньев 7-8 звено 2 |
| Рис. 2.9 |
После таких изменений классов КП подвижность механизма
Контрольные вопросы к лекции 2.
Избыточные связи и лишние степени свободы в узлах и механизмах
Правило:
Избыточными связями называют такие связи, устранение которых не увеличивает подвижность механизма.
Рассмотрим некоторые механизмы без избыточных связей на нескольких примерах:
1. Всем известный кривошипно-шатунный механизм любого двигателя внутреннего сгорания, в нем поршень прикреплен к одному шатуну. Шатун накладывает четыре связи на поршень, пятая приобретается малым осевым зазором между ним и поршнем. Этих связей достаточно для работы механизма, шестая связь будет блокировать вращение поршня в головке шатуна. Такая схема допускает изменения длины шатунов от номинала в пределах большого допуска, на работоспособность ДВС это не отразится. Допустим, по каким-то причинам нам потребовалось к поршню (ползуну) прикрепить несколько шатунов, тогда разница длины шатунов должна лежать в пределах нескольких микрон, иначе нагрузка между ними будет неравномерной, что приведет к лишним напряжениям и перекосам.
 |
| Рисунок 1 |
 |
| Рисунок 2 |
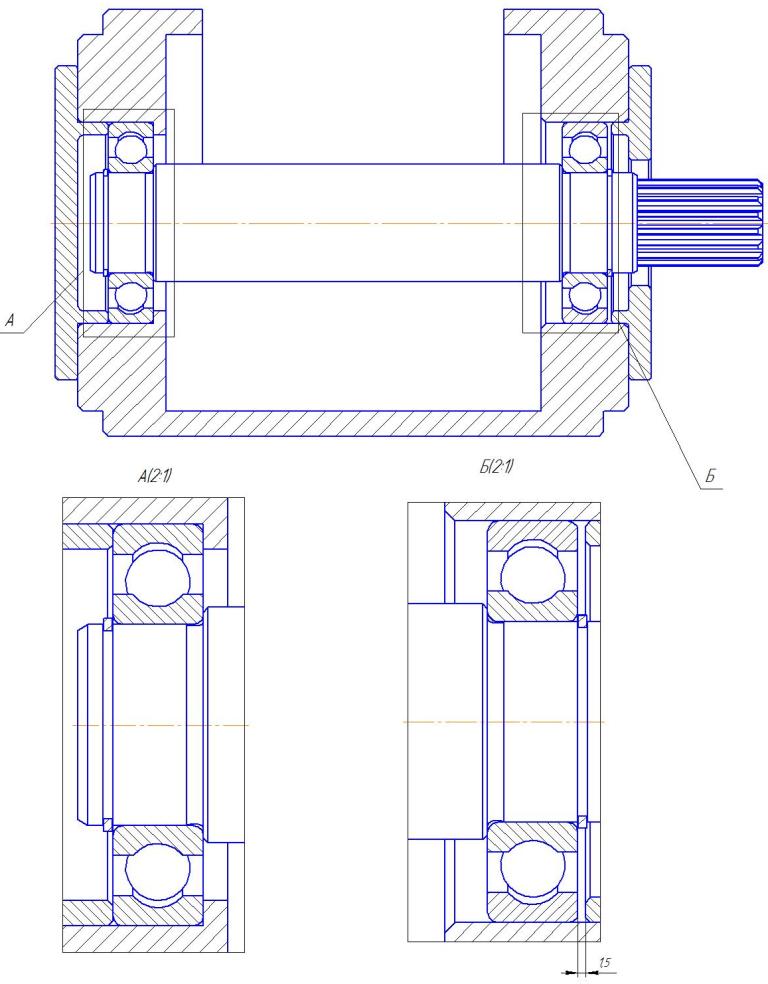
В качестве примера такого механизма возьмем газораспределительный механизм, распределительный вал которого вращается на нескольких подшипниках (обычно 4 или 5). Нормальная работоспособность такого механизма достигается только высокой точностью изготовления как самого вала, так и подшипников, поэтому стоимость распределительного вала очень высока.
3. Многие знают, как качается на кухне стол и для того, чтобы он не качался, устанавливают под одну из ножек сложенную газету или спичечный коробок. Такое поведение стола как раз вызвано избыточностью одной ножки. Именно поэтому все рояли имеют три ножки.
Как показывает этот принцип, статически неопределимые звенья применять нежелательно. Исключение необходимо делать только в том случае, если в них установлены пружины или звенья работают на изгиб с большими деформациями.
Если механизм статически определим, то размеры звеньев почти не влияют на передаваемые силы, поэтому допуски на размеры могут лежать в больших пределах. К этому необходимо стремиться всем конструкторам.
Приведенные примеры позволяют сформулировать два основных правила конструирования самоустанавливающихся механизмов:
Каждый вал необходимо устанавливать на два подшипника;
Недопустимо применять сдвоенные механизмы, при одинаковых начальных и конечных звеньях нельзя между ними устанавливать два передаточных механизма.
Автор статьи: Vdovinea
(Статья написана с использованием трудов Решетова Л.Н.)
Выявление избыточных связей и их устранение
Для повышения надежности рекомендуется применять механизмы статически определимые, т.е. без избыточных (пассивных) связей. Такие механизмы называют рациональными.
Избыточные (пассивные) связи – это связи, устранение которых не увеличивает подвижности механизма. Они вредны, так как увеличивают требования к точности изготовления звеньев, снижают надежность работы механизма.
Проверить механизм на наличие в нем избыточных связей можно путем подсчета их по структурным формулам, одна из которых предложена А.П. Малышевым:
Другую формулу предложил О.Г. Озол
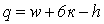
где к – число независимых контуров в механизме 
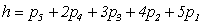
При конструировании рационального механизма надо уметь определить в каком замкнутом контуре имеются избыточные связи и какие они. Сделать это можно используя матричный метод определения структурных свойств механизма. Формула Озола и Малышева позволяют установить лишь число избыточных связей в механизме.
Матричное уравнение для определения избыточных связей механизма имеет вид
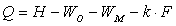
где 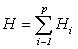
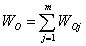
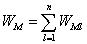
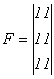
Для выявления избыточных связей следует заменить отсутствующие поступательные и вращательные подвижности имеющимися поступательными и вращательными подвижностями вдоль осей не перпендикулярных направлениям отсутствующих подвижностей. Кроме того, отсутствующие поступательные подвижности необходимо заменить имеющимися в наличии вращательными в соответствии с таблицей 7.
Таблица 7 Таблица замены поступательных подвижностей вращательными
| tx | ty | tz | |
| rx | _ 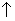 | _ 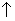 | |
| ry | _ 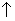 | _ 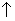 | |
| rz | _ 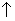 | _ 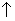 | _ 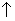 |
Таким образом, в матрице подвижностей отрицательные элементы первого столбца могут быть заменены положительными элементами второго столбца, лежащими в других строках, например:
Одной угловой подвижностью можно заменить только одну отсутствующую поступательную подвижность, отмеченную в матрице отрицательным значением соответствующего элемента. В результате матрица преобразуется к виду:
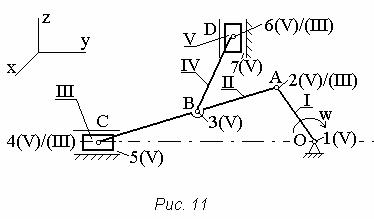
Рассмотрим пример исследования подвижностей и избыточных связей для механизма, кинематическая схема которого показана на рис.11.
Заданный механизм имеет: 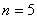
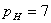
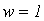
Для всех звеньев рассматриваемого механизма местные подвижности отсутствуют, и суммарная матрица местных подвижностей имеет вид:
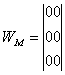
Суммарная матрица общих подвижностей:
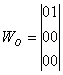
Все кинематические пары 5-го класса 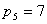
Определим число избыточных связей по формуле Малышева:
Определим по формуле Озола число избыточных связей.
Здесь
Сумма подвижностей для семи кинематических пар 5-го класса будет равна семи, так как каждая пара имеет по одной подвижности.
Тогда 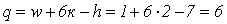
Мы установили только число избыточных связей в механизме.
Матричный метод позволяет определить какие избыточные связи имеются в механизме. Матрицы подвижностей кинематических пар имеют вид:
Суммарную матрицу подвижностей кинематических пар найдем:
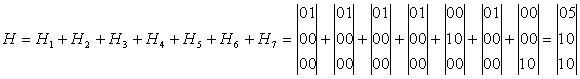
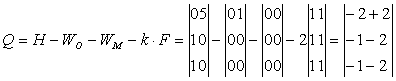
Произведем замену отсутствующих поступательных подвижностей угловыми:
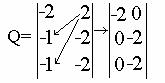
Определим число избыточных связей по формуле Малышева:
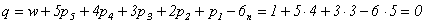
Определим число избыточных связей по формуле Озола:

Убедимся, что избыточные связи отсутствуют, используя матричный метод:

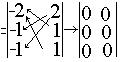
Для механизмов, в которых используются только кинематические пары 3, 4 и 5-го класса, можно использовать простое соотношение, облегчающее правильный выбор классов кинематических пар кинематических групп Ассура. Кинематическая группа не вносит избыточных связей при присоединии к механизму, если для нее выполняется соотношение:
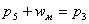
где 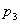
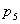
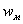

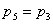
Данные соотношения будут выполняться и в том случае, когда все кинематические пары четвертого класса, а местные подвижности звеньев отсутствуют. Приведенная зависимость позволяет правильно соориентироваться при выборе классов кинематических пар групп Ассура. Проверку структурных свойств полученного механизма и уточнение классов кинематических пар следует провести используя матричный метод.
Макеты механизмов, масштабная линейка, транспортир, циркуль, карандаши.
Последовательность выполнения работы
1. Ознакомиться с моделью механизма, установить его назначение (например, преобразование вращательного движения в поступательное), определить число звеньев и кинематических пар. Составить кинематическую схему механизма без учета масштаба, обозначив на ней размеры, подлежащие измерению.
2. Измерить расстояние между центрами шарниров, расстояние до неподвижных направляющих, углы между плечами звеньев. Составить таблицу параметров звеньев механизма.
3. Выделить неподвижные элементы кинематических пар, принадлежащие стойке (базовые точки и линии) и нанести их на схему с учетом выбранного масштабного коэффициента длинны 
4. Вычертить одно из положений ведущего звена, при котором в механизме нет наложения одного звена на другое. Показать стрелкой направление движения ведущего звена.
5. В выбранном масштабе вычертить кинематическую цепь, образованную остальными звеньями механизма, используя метод планов положений звеньев.
6. Пронумеровать звенья римскими цифрами, а кинематические пары – арабскими цифрами. Кроме того, центры вращательных кинематических пар обозначить прописными буквами латинского алфавита. Указать масштабный коэффициент длинны, использованный при построении кинематической схемы.
7. Составить структурную схему механизма.
8. По структурной формуле Малышева определить степень подвижности механизма.
9. Составить таблицы звеньев и кинематических пар, определив вид пары (вращательная или поступательная), а также указать номера звеньев, образующих эти пары.
10. Провести структурный анализ по Ассуру:
а) разбить механизм на группы Ассура (w=0);
б) каждую группу вычертить в том виде, в каком она изображена на схеме механизма, а также нарисовать структурные схемы (детльную и укрупненную) составных частей механизма, выделенных на основе структурных группы.
в) для каждой группы определить:
— число подвижных звеньев n,
— число низших кинематических пар pH,
— степень подвижности w,
— вид (модификацию), если группа 2-го класса.
11. Написать формулу строения механизма.
12. Определить класс и порядок механизма.
13. Нарисовать укрупненную структурную схему механизма.
14. Нарисовать конфигурации механизма: а) считая, что составными частями первого уровня разукрупнения являются его звенья; б) считая, что составными частями первого уровня являются сборочные единицы, выделение в результате структурного анализа по Асуру, а составными частями второго уровня – звенья.
Следующие пункты выполняют студенты, у которых нет домашнего задания по структурному анализу механизма матричным методом.
1.В заданном механизме при известных кинематических парах (все кинематические пары 5-го класса) определить число избыточных связей по формулам Малышева, Озола и матричным методом.
2. Выполнить замену кинематических пар с целью полного устранения избыточных связей (q=0). По формулам Малышева, Озола и матричным методом проверить отсутствие избыточных связей.
1. Что называется машиной, механизмом?
2. Чем звено может отличаться от детали?
3. Входные и выходные звенья, ведущие и ведомые звенья, начальное звено механизма.
4. Особенности звеньев вида: кривошип, коромысло, кулиса, шатун, ползун.
5.Что называется кинематической парой?
6. Чем определяется класс кинематической пары?
7. Что такое элемент звена (элемент кинематической пары)?
8. Что такое узел сопряжения звена?
9. Чем отличается узел сопряжения от элемента звена?
10. Какие кинематические пары являются высшими, низшими?
12. Напишите и объясните структурную формулу Сомова – Малышева.
13. Что такое кинематическая группа Ассура?
14. Как связано число звеньев и число кинематических пар группы Ассура?
15. Чем отличаются группы Ассура от составных частей механизма, соответствующих этим группам?
16. Как определяется класс кинематической группы Ассура?
17. Как определяется порядок групп Ассура?
18. Какая кинематическая цепь является статистически определимой?
19. Что такое избыточные (пассивные) связи?
20. Что такое избыточные групповые подвижности звеньев?
21. Зачем необходимо знать, где и какие возникают лишние связи и избыточные местные подвижности?
22. По какой формуле можно определить число избыточных связей в механизме?
23. Как устранить лишние пассивные связи и избыточные местные подвижности?
24. Как проявляются при сборке избыточные связи?
25. Напишите матрицу подвижностей кинематической пары: вращательной, поступательной, сферической и т.д.?
26. Какие элементы матрицы структурных параметров показывают избыточные связи, а какие избыточные групповые подвижности звеньев?
27. Что такое местные подвижности звеньев?
28. Когда возможна замена отсутствующих поступательных подвижностей вращательными?
29. Что такое кинематическая схема, структурная схема и конфигурация механизма?
Лабораторная работа №7
Дата добавления: 2019-02-22 ; просмотров: 2099 ; Мы поможем в написании вашей работы!
Избыточные (пассивные) связи и местные подвижности
В механизме могут иметь место избыточные (пассивные) связи и пассивные (локальные, местные) подвижности, не влияющие на движение механизма в целом и на закон движения входного звена.
Избыточные связи в механизме – повторяющиеся (или зависимые) связи, удаление которых не изменяет заданного числа степеней свободы механизма. Отклонения в расположении связей компенсируются деформациями звеньев, износом контактирующих поверхностей зазорами между элементами кинематических пар, повышенной точностью изготовления и сборки звеньев, кромочным контактом элементов пар. Структурная схема механизма без избыточных связей называется основной схемой.
Пассивные связи могут быть полезными и вредными.
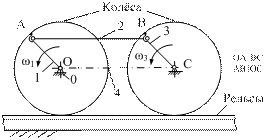
Полезные пассивные связи вводятся конструктором в схему механизма искусственно для улучшения конструкции механизма (повышения нагрузочной способности и надежности). На рис. 7 изображена схема механизма параллельных кривошипов (применяется в качестве привода ведущих колес тепловозов).
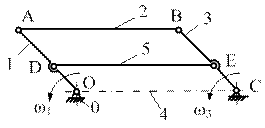
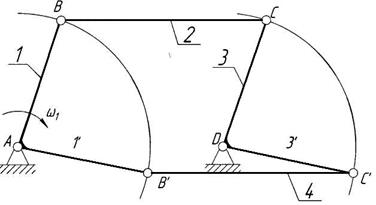
а) в крайнем положении механизма, возможно положение, при котором кривошипы 1, 3 и шатун 2 будут находиться на одной прямой, совпадающей с ОС. При дальнейшем движении кривошипа 1 возможен переход механизма параллелограмма в механизм антипараллелограмма. Неоднозначность движения звена 3 сопровождается резким ухудшением передачи сил в механизме. На практике указанные недостатки устраняют, вводя в схему механизма дополнительное «лишнее» звено 5 (рис. 8), или звено 4(рис.9), т.е. вводя связи, налагаемые или пассивные.
Рис. 8 Механизм параллелограмма с дополнительным звеном
Рис.9 Механизм параллелограмма с дополнительным звеном
б) Тепловоз – энергоемкая машина, поэтому нагрузки, приходящиеся на шатун, соединяющий и обеспечивающий одинаковое вращение ведущим колесам (ω1 = ω3) тепловоза, достаточно велики. В результате не исключена деформация или утрата прочности шатуна из-за его перегрузок (т.к. размеры и сечение кривошипов ограничены габаритами колес подвижных составов). Подвижность механизма с пассивными связями:
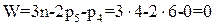
Если судить по результатам расчета, то внедрение в схему (Рис.8) механизма дополнительного звена 5 лишило механизм подвижности, обратив его в ферму. В действительности же введение в схему звена 5 при выполнении условия, что 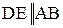
Отсюда следует вывод: при определении подвижности механизма по структурной формуле пассивные связи не должны учитываться – они должны быть выявлены и мысленно отброшены.
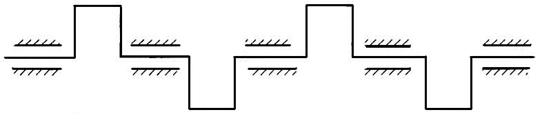
«Лишние» звенья используются достаточно часто в механизмах для повышения их жёсткости и улучшения условий передачи сил. Повышение жёсткости и несущей способности звеньев достигается путём введения дополнительных кинематических пар (Рис.10).
Рис. 10 Схема многоопорного коленчатого вала двигателя
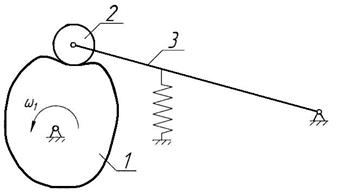
При проектировании механизмов износ рабочих поверхностей деталей уменьшают за счёт установки звеньев, имеющих местную подвижность. Роль промежуточных звеньев выполняют детали, движение которых не влияет на кинематику механизма в целом. Наиболее распространёнными промежуточными деталями являются шарики подшипников винтовых передач, ролики подшипников зубчато-роликовых передач и кулачковых механизмов. Так установка ролика 3 в кулачковых механизмах (Рис.11.) не изменяет первоначально принятого закона движения толкателя 2. Степень подвижности механизма по формуле Чебышева:
Рис. 11 Схема кулачкового механизма с роликовым толкателем
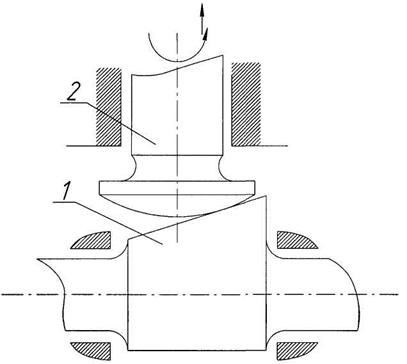
Дополнительная, местная подвижность, получаемая при вращении ролика вокруг своей оси, существенно снижает трение в механизме, но огранка ролика при износе или погрешностях изготовления механизма может существенно исказить ранее принятый закон движения. В кулачковом механизме с плоским толкателем трение в высшей паре уменьшается при использовании сферического толкателя и скошенного профиля кулачка (Рис.12.). При вращении кулачка – 1, толкателю – 2 сообщается не только основное движение вдоль его оси и дополнительное вращение, вследствие чего износ профилей уменьшается.
Рис 12 Схема кулачкового механизма со сферическим толкателем и скошенным кулачком