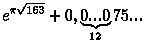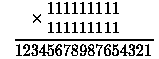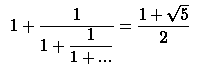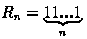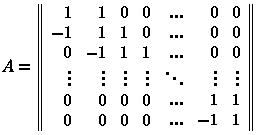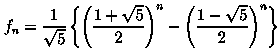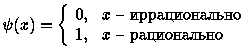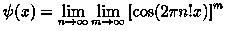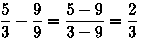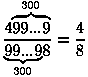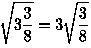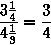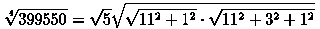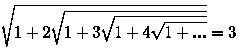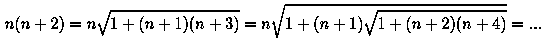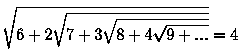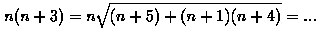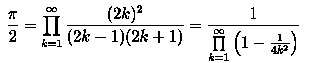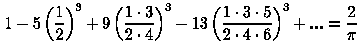что такое интересное число
13 самых знаменитых чисел
Арифметика на грани астрологии.
Дизайнеры всего мира знают: чёрный — цвет скорби, зелёный — цвет спокойствия, а голубой — цвет динамичного развития компании, молодой коллектив которой бесстрашно смотрит в будущее и не боится задержек зарплаты. И дизайнерам всего мира приходится с этими догмами работать.
Такая же история и с числами: в Китае не бывает 4-х этажей (звучит как «смерть»), 18-й — самый долгожданный день рождения, а длина и радиус одной окружности никогда не будут целыми числами одновременно. Список из самых интересных и загадочных чисел прилагается:
Пи: 3,14
Известная всем со школы константа, определяющая коифициент отношения длинные окружности к радиусу. Единственное число в списке, имеющее собственный праздник: 14 марта (то есть 3 месяц, 14 число).
Число действительно очень интересное, математики продолжают изучать его свойства до сих пор. Например, Пи — удивительно нормальное число. То есть в его десятичной записи на 200 млн знаков после запятой примерно равномерно встречаются все десять цифр.
Число Эйлера (e): 2,71
Ещё одна школьная константа, более известная, как основание логарифма. Так же как и Пи, вызывает неугасающий интерес учёных, и примерно те же самые вопрос. Кроме того, математикам так и не удалось обосновать какую-то связь Пи и e.
666
В Библии фигурирует как «число, под которым скрыто имя зверя Апокалипсиса». «Здесь мудрость. Кто имеет ум, тот сочти число зверя, ибо число это человеческое; число его шестьсот шестьдесят шесть». (Отк. 13:18). Какого именно зверя — не очень ясно, потому что в «Откровении Иоанна Богослова» их четыре: орел, лев, ангел и бык. Число стало символизировать что-угодно антихристианское, и его немедленно забронировали себе в качестве официального атрибута сатанисты.
Как считают некоторые теологи, в числе зашифровано имя, но какое именно — не ясно.
К слову, в Библии три шестерки встречаются три раза и в «Ветхом завете».
13
Историки не могут точно сказать, откуда взялась боязнь числа 13, но, чтобы не выглядеть глупо, придумали явлению название — «трискайдекафобия». Самая известная версия — это отсылка к Библии, на Тайной вечере Иуда был 13-м.
Уровень боязни числа прямо пропорциональна религиозности страны: больше всего попыток заменить число 13 разными способами (12+1, 12B и т.п.) в Италии и США.
18
Возраст совершеннолетия в самом большом количестве стран. Чаще всего после этого возраста молодым людям разрешают голосовать, заключать браки, начинать собственное дело и платить налоги.
Очевидно, что 18 оборотов вокруг Солнца, которые сделал гражданин никак не гарантируют его дееспособность, поэтому до сих пор остаётся предметом спора.
Гугол
Это единица с сотней нулей после неё. Название в шутку придумал математик Эдвард Казнер в 1938 году, когда гулял с племянниками, а те донимали его вопросом «какое самое большое число?» 60 лет спустя два молодых человека назвали так собственный поисковый движок.
Ноль
Самое важное, что нужно знать про ноль — это то, что него нельзя делить. На компьютерах и калькуляторах эта функция заблокирована, потому что может сломать Вселенную.
8
7 — счастливое число в Западной культуре (тоже по библейским мотивам), но надежды, возлагаемые на него, не могут сравниться с тем, как боготворят восьмёрку Китайцы. На мандарине цифра 8 (八) читается как «ба», что созвучно с иероглифом 发, который читается как «фа». У него невероятное количество значений, но китайца больше всего интересует комбинация 发财 — богатеть. Почти все цены в Китае заканчиваются на восьмерку, а половина работодателей выплачивает зарплату суммами, заканчивающимися на 88. Потому восьмерок в Китае много не бывает.
Золотое сечение: 1,618
Самое творческое число, популяризированное Леонардо да Винчи. Встречается практически везде: и в химических структурах, в биологии, физиологии и т.д.
В реальной жизни начали применять ещё до изобретения самого термина «математика». Самый известный пример — пропорции египетских пирамид.
Числа Фибоначчи: 1, 1, 2, 3, 8, 13, 21, …
Ряд Фибоначчи — это по сути выраженное числами золотое сечение. Записывается очень легко: первые два числа — это единицы, а каждое последующее — это сумма предыдущих.
Последовательность придумали в Древней Индии, но в Европе её популяризовал Леонардо Пизанский в XI веке н.э. Эта последовательность чисел очень часто встречается в природе: согласно этой формуле располагаются семена подсолнуха, семена в шишках, ячейки ананаса и т.д. Даже длины фаланг пальцев у человека подчинены этой последовательности.
43252003274489856000
Количество комбинаций трёхсекционного Кубика Рубика. Нынешний рекорд сборки составляет 3,47 секунд, то есть нынешний чемпион сможет перебрать их все всего за 4,8 млрд лет.
12
Дюжина долгое время претендовала на то, чтобы стать основой для универсальной системы исчисления. Отсюда и такое количество рядов с двенадцатью пунктами: часы, месяцы, апостолы (Иуда не считается), боги в греческом пантеоне, ступень колеса в буддизме, имамов в буддизме, дюймов в футе, пунктов в кегле, пенсов в шиллинге, и т.д.
Есть мнение, что десятеричная система закрепилась только из-за того, что у нас на руках 10 пальцев, но для двенадцатеричной системы существовал свой способ демонстрации чисел: по количеству фаланг на четырех (кроме большого) пальцах руки.
42
42 — это ответ на главный вопрос жизни, вселенной и всего такого по версии писателя-фантаста Дугласа Адамса. Получен в результате вычисления семи с половиной миллионов лет непрерывных вычислений на специальном компьютере «Думатель». Ответ должен был решить практически все проблемы Вселенной.
Развитые расы, получившие ответ 42 были несколько разочарованы, тогда «Думатель» предложил создать ещё более совершенный компьютер, который найдёт Окончательный Вопрос. Компьютер назвали Земля. Что было дальше — читай в романах серии «Автостопом по галактике».
Что такое удивительные числа?
Числа пронизывают все сферы жизни человека. Еще великий Пифагор утверждал, что все вещи в мире можно представить в виде чисел. Посредством производящих счет величин человечеству удалось определить целый ряд вселенских законов и разгадать тайны в истории. Но даже среди них встречаются самые необычные. Что же такое удивительные числа и чем они отличаются от обычных величин?
Удивительные свойства простых чисел
Многие наверняка замечали, что порой приходится удивляться не сложному, а простому. Это же правило распространяется и на мир чисел.
Простыми числами принято считать натуральные величины, которые способны делиться только на самих себя и на единицу. Среди них встречаются удивительные числа-близнецы – пары, которые различаются на 2. К примеру: 5 и 7; 11 и 13; 17 и 19. На рубеже первой сотни насчитывается всего 8 таких пар. По мере дистанцирования от нулевой отметки количество пар сокращается. Примечательно, что близнецы могут образовывать сосредоточения, формируя «четверки», например: 11, 13, 17, 19. Сколько же таких скоплений можно сформировать пока неизвестно.
В математике существует такой термин как «проблема Гольдбаха». Суть ее в том, что еще в 1742 г. Гольдбах, бывший на тот момент членом Петербургской Академии наук, заметил, что любая целая величина натурального ряда, вышеследующая за пятеркой, являет собой сумму, включающую максимум три слагаемых из простых чисел. К примеру: 34=31+3, 52=48+4…
Ученый испытал множество величин. И каждая из них представляла собой сумму, включающую 2 или 3 слагаемых.
Российский математик Л.Эйлер пошел еще дальше, предположив, что любое четное число натурального ряда, вышеследующее за двойкой, являет собой сумму из слагаемых, представленных двумя простыми числами. Это: 28=11+17=23+5; или 12=5+7; 64=59+5=41+23=47+17.
Открытия о составных числах
Не меньше вопросов и споров возникает при изучении составных чисел – величин, имеющих более двух делителей.
Замечательные «смиты»
Так именуют подкатегорию составных чисел, сумма цифр которых в десятичной системе исчисления соответствует сумме цифр его простых сомножителей при условии учета кратности. Их существует бесконечно много, но все они компактно упакованы посредством степеней. Чаще всего их можно наблюдать среди фигурных: 22 – пятиугольное, 378 – треугольное, 121 – квадратное.
Наглядным примером может служить равенство 2х101=202, поскольку каждая из его сторон по обе стороны «=» соответствуют «4». Так 2+0+2=4, и 2+1+0+1= 4.
В семействе «смитов» встречается немало диковинок:
Настоящими «изюминками» этого семейства выступают десятизначные величины, при написании которых каждая цифра используется лишь единожды. К примеру: 9 876 542 103 и 1 023 465 798.
Цикличность величины 142857
Одним из самых удивительных чисел по праву можно считать 142857. Оно необычно тем, что при умножении каждой из первых шести величин натурального ряда на него в результате будет получаться цилиндрический сдвиг этого шестизначного числа. В ответе каждый раз будут присутствовать одни и те же цифры, только они будут смещаться, двигаясь по типу ленты.
Секрет такой удивительной периодичности кроется в том, что 142857 выступает периодом преобразования простой дроби 1/7 в десятичную. Поэтому значения, расположенные после знака «=» являются периодами дробей: 1/7, 2/7, 3/7…
Число Шахерезады
Не менее интересно и «число Шехеризады». Именно оно проходит лейтмотивом через сборник арабских сказок «Тысяча и одна ночь». Но удивительно оно по той причине, что наделено целым рядом уникальнейших свойств. Перечислим лишь основные среди них:
1001 – палиндром или перевертыш. Оно отличается симметрией записи и потому читается одинаково в обоих направлениях. К примеру:
Еще одно удивительное свойство 1001 – при умножении на него любой трехзначной величины в результате получается та же самая величина, только прописанная дважды. К примеру: 756х1001=756756. Зная эту закономерность, у любого желающего не составит труда умножать на 1001 любые трехзначные величины.
Золотое сечение
Что объединяет пальцы человеческой ладони и спирали улитки, древнеегипетские пирамиды и произведение «Мона Лиза»? Ответ кроется в удивительных числах, а точнее их последовательности, которые являются божественной мерой красоты.
Последовательность, именуемая как ряд Фибоначчи, уникальна тем, что каждое «звено цепи» образуется из суммы двух предыдущих. Вот как выглядит эта цепочка: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, …
Составляющие ее величины имеют еще одну интересную особенность. Если разделить любую величину из «цепи» на предшествующую ей, в ответе всегда будет значение, максимально приближенное к иррациональному числу, десятичное представление которого всегда не периодично и бесконечно. Это 1.61803398875…
Это соответствие частей называется Золотое сечение. 1,6180339887 – величина, которая очерчивает совершенные универсальные пропорции в изобразительном искусстве и науке. Считается, что две величины находятся в Золотой пропорции, если их коэффициент к большей является точно таким же, как и соразмерность между большей и меньшей. Варианты таких соразмерностей:
Формообразующий закон симметрии с удивительной настойчивостью проявляется в объектах, несущую эстетическую ценность у разных народов и эпох. Исходя из общепринятой пропорции, свои расчеты сегодня производят ученые.
Дизайнеры и модельеры берут за основу мерки с фигуры человека, которая построена по закону Золотой пропорции. Вот лишь некоторые соотношения 1:1.618, которые неизменно прослеживаются в теле любого человека. На голове это расстояние:
Ведь многочисленные исследования подтверждают: если пропорции любых частей тела приближены к пропорции золотого сечения – получается идеальное телосложение, что выступает ключевым критерием красоты.
Математическая константа Пи
Самая популярная математическая константа выражает соотношение окружности к диаметру круга. Буквенное обозначение константы и образовано от первых букв греческих слов, обозначающих «периметр» и «окружность».
Главное свойство этого удивительного числа в том, что оно никогда не кончается и не повторяется. Первые 50 символов после знака препинания имеют такой вид:
Максимальное количество цифр Пи после запятой рассчитал посредством сверхмощного компьютера японский ученый в 2011 г. Их количество составляет 10 трлн. цифр. В процессе работы он вывел интересное статистическое наблюдение. В первом млн. знаков после запятой присутствует:
Пи применяют в областях, требующих максимальной вычислительной мощности: при составлении прогноза погода, в мировой социально-экономической статистике. Наглядным воплощением величины Пи является и пирамида Хеопса в Каире. Соотношение высоты постройки с периметром основания создает это Пи.
Распространенные числовые суеверия
Предубеждения, связанные с удивительными свойствами чисел – одни из самых распространенных и долгоживущих. У многих из нас есть свое любимое число, которое непременно приносит удачу. Все это отголоски представлений наших предков о мистической силе производящих счет величин.
Священное число 7
7 выступает основным положением любой религии в мире. 7 добродетелей у христиан, 7 райских врат в исламе, 7 сокровищ чакравартина в буддизме…
Божественное число символизирует гармонию и совершенство:
Но главная причина особого значения этой величины в жизни людей в том, что все живые существа живут по лунному циклу. Он состоит из 4 фаз, каждая из которых включает 7 дней.
Исследования демонстрируют, что 7 – эквивалент максимальной вместительности оперативной памяти мозга. Из 10 представленных предметов или произнесенных слов человек может восстановить в памяти толь ко 7. Для реализации творческого труда оптимальное количество участников дискуссионной группы также составляет 7. Если в переговорах участвует более чем 4 человек, то коллектив автоматически распадется на группы по интересам.
Число Зверя
666 – составное число Смита удивительно тем, что его можно записать в двух вариантах при возрастающем порядке, используя для этого 9 неповторяющихся цифр, и одним вариантом в убывающем:
К тому же эта величина выступает:
Но для большинства людей эта величина известна под названием как «число Зверя». В Библии «7» упоминается как чистота и полноценность. Это 7 дней сотворения, 7 смертных грехов, 7 таинств. Шестерка – наоборот, нечто неполное и несовершенное, подобно Божему врагу.
Троекратность в 666 оказывает усиливающий негативный эффект, делая его символом крайней степени несовершенства. Обладает ли разрушительной силой эта величина доподлинно неизвестно. Но с десятки сотен фактов связанные с его негативным воздействием в истории человечества все же наберется.
Чертова дюжина
С точки зрения математики 13 это:
Людей, испытывающих ужас перед чертовой дюжиной, называют трискаидекафобами. Чтобы их не нервировать, многие европейские дома пронумерованы, минуя эту цифру, а во многих зданиях после 12-го этажа сразу следует 14-й. Отсутствует эта цифра и в нумерации кают на морских суднах, 13-й ряд зачастую отсутствует в самолетах.
При кажущейся простоте мир полон загадок и тайн. Но разгадать их под силу только самым пытливым умам.
Что такое интересное число
Скопировано с http://avva.narod.ru с разрешения автора, спасибо Алексею Амилющенко.
Все про числа
Не могу удержаться от того,
чтобы не сослаться на
замечательную песню
Александра Дольского «Арифметика».
Можно считать, что эта песня
является эпиграфом к данной странице.
Текст песни и ее запись
в формате Real Audio
можно посмотреть здесь.
Про каждое число можно рассказать что-то интересное. Каждое число чем-то отличается от других, а чем-то и похоже. На этой странице я планирую помещать описания интересных свойств (на мой взгляд, конечно) чисел.
Постоянная Капрекара
1118 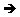
11118 
123 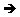
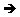
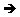
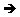
Числа Армстронга
| n | Числа Армстронга | n | Числа Армстронга | |
| 3 | 153; 370; 371; 407 | 8 | 24678050; 24678051; 88593477 | |
| 4 | 1634; 8208; 9474 | 9 | 146511208; 472335975; 534494836; 912985153 | |
| 5 | 54748; 92727; 93084 | 10 | 4679307774 | |
| 6 | 548834 | 11 | 32164049650; 32164049651; 40028394225; 42678290603; 44708635679; 49388550606; 82693916578; 94204591914 | |
| 7 | 1741725; 4210818; 9800817; 9926315 | 14 | 28116440335967 | |
| Более полный список чисел Армстронга можно найти в еженедельнике «Компьютерра» #25 от 23 июня 1997 г. | ||||
Самопорожденные числа
Самопорожденные числа:
11 111 111 111 111 111 111 и 3 333 333 333
| 10 | порождено числом | 5 |
| 100 | порождено числом | 86 |
| 1 000 | порождено числом | 977 |
| 10 000 | порождено числом | 9 968 |
| 100 000 | порождено числом | 99 959 |
| «Циклическое» число 142857 |
При умножении числа 142857 на числа от 1 до 6 получается произведение, записанное теми же цифрами, переставленными в циклическом порядке:
142857 x 1 = 142857;
142857 x 2 = 285714;
142857 x 3 = 428571;
142857 x 4 = 571428;
142857 x 5 = 714285;
142857 x 6 = 857142.
Что интересно, если умножить 142857 на 7, то получится число 999999.
Число 142857 совпадает с периодически повторяющейся последовательностью цифр, стоящих в дробной части числа 1/7, записанного в десятичной форме.
Почти целое число
262 537 412 640 768 744 =
Число 45 можно представить как сумму совершенно не целых слагаемых:
Заметьте, что слагаемых в этой сумме также ровно 45.
А вот просто красивый пример на умножение:
Впрочем, подобных примеров довольно много и они не менее красивы:
12345679 x 9 = 111111111
12345679 x 8 = 98765432
Умножение на единицу
Как получить любое число используя только три двойки
Очевидно проверяется, что любое число можно получить используя только три числа 2 и конечное количество математических знаков:
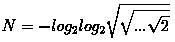
Корень из двух в двоичной записи
Числа словами
В этой фразе двадцать восемь букв.
Это предложение содержит двенадцать слов, двадцать шесть слогов и семьдесят три буквы.
В этой фразе два раза встречается слово «в», два раза встречается слово «этой», два раза встречается слово «фразе», четырнадцать раз встречается слово «встречается», четырнадцать раз встречается слово «слово», шесть раз встречается слово «раз», девять раз встречается слово «раза», семь раз встречается слово «два», три раза встречается слово «четырнадцать», три раза встречается слово «три», два раза встречается слово «девять», два раза встречается слово «семь», два раза встречается слово «шесть».
Девять слов назад это предложение еще не началось.
Вы только что начали читать предложение, чтение которого Вы уже заканчиваете.
Логическое противоречие
То, что написано на этой странице неправда!
Закон экономики
При снижении цены на 20%, количество товара покупаемого на одно и то же количество денег возрастает на 25%.
«Золотое сечение», записанное в виде цепной дроби
Как получить что-то иррациональное используя только единицы:
Куда ни читай, а все квадрат получается (да и квадрат-то тоже можно в любую сторону читать)
| 113 2 =12769 | 96721=311 2 |
| 112 2 =12544 | 44521=211 2 |
| 122 2 =14884 | 48841=221 2 |
| 1212 2 =1468944 | 4498641=2121 2 |
| 1112 2 =1236544 | 4456321=2111 2 |
Репьюниты
Число называется репьюнитом, если оно составлено из одних единиц. Например, 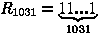
Общий вид репьюнита:
Числа Смита
Число называется числом Смита, если сумма цифр числа равна сумме цифр разложения этого числа на простые множители. Например:
Числа Фибоначчи
Число называется числом Фибоначчи, если оно является одним из членов последовательности:
Однако не все знают, что (n+1)-й член ряда Фибоначчи можно получить, вычислив определитель матрицы размером (n x n):
Можно также определить n-й член ряда Фибоначчи, непосредственно подсчитав выражение:
| Числа 0 и 1 и функция Дирихле |
Не очевидно, что саму функцию Дирихле можно записать в аналитическом виде:
«Неправильные» вычисления иногда бывают правильными
Выражение: 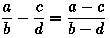
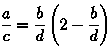
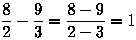
Известно, что для приведения дроби к простому виду, нужно выделить в числителе и знаменателе одинаковые множители и их сократить. Некоторые этого не делают, а просто зачеркивают одинаковые цифры. И что самое удивительное также бывают (иногда) правы:




Известно, что при извлечении корня из дроби нужно проявить некоторую осторожность. Некоторые этого не делают. И что самое удивительное и они бывают (иногда) правы:
Известно, что деление дробей сводится к умножению обратных дробей. Некоторые этого не делают, а просто зачеркивают «лишние» части. И что самое удивительное, даже они бывают (иногда) правы:
Красивое разложение корня четвертой степени из числа 399550 :
Число 3 получается из забавной формулы:
Эта формула является следствием более общей формулы при n =1 :
Очень похоже (и так же красиво) выглядит запись числа 4 :
Это также следствие более общей формулы при n =1 :
| Еще про числа 3 и 4 |
Несколько утверждений про числа
Любое нечетное число можно представить в виде разности квадратов двух чисел.
Например:
Любое натуральное число, кратное 4, можно представить в виде разности квадратов двух чисел.
Например:
Любое натуральное число, дающее в остатке 1 при делении на 4, можно представить в виде суммы двух квадратов.
Например:
4 + 6 = 10 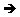
33 + 7 = 40 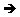
432 + 18 = 450 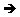
Или так:
Про простые числа можно говорить бесконечно (не в том смысле, что самих простых чисел бесконечно много и было бы просто тривиально начать их перечислять, а в смысле, что у простых чисел очень много интересных свойств).
Известна, например, теорема П. Л. Чебышева, что между двумя натуральными числами n и 2 n имеется по крайней мере одно простое число.
Вот список всех простых чисел от 0 до 2000:
1 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997 1009 1013 1019 1021 1031 1033 1039 1049 1051 1061 1063 1069 1087 1091 1093 1097 1103 1109 1117 1123 1129 1151 1153 1163 1171 1181 1187 1193 1201 1213 1217 1223 1229 1231 1237 1249 1259 1277 1279 1283 1289 1291 1297 1301 1303 1307 1319 1321 1327 1361 1367 1373 1381 1399 1409 1423 1427 1429 1433 1439 1447 1451 1453 1459 1471 1481 1483 1487 1489 1493 1499 1511 1523 1531 1543 1549 1553 1559 1567 1571 1579 1583 1597 1601 1607 1609 1613 1619 1621 1627 1637 1657 1663 1667 1669 1693 1697 1699 1709 1721 1723 1733 1741 1747 1753 1759 1777 1783 1787 1789 1801 1811 1823 1831 1847 1861 1867 1871 1873 1877 1879 1889 1901 1907 1913 1931 1933 1949 1951 1973 1979 1987 1993 1997 1999
Принимаются замечания, дополнения, исправления. Присылайте файлы в формате MS WORD или TeX Алексею Амилющенко. В письме либо укажите доказательство, либо ссылку на источник, где оно было опубликованно.
Приведенные выше опыты с числами были описаны в следующих печатных изданиях: журнале «Техника-Молодежи», журнале «Scientific American», газетах «Пионерская правда» и «Неделя», журнале «Квант», а также в учебнике В. А. Зорича «Математический анализ», в задачнике по функциональному анализу Кириллова и Гвишиани, в замечательных книгах М. Гарднера («От мозаик Пенроуза к надежным шифрам», «Путешествие во времени» и др.), в книге «Киевские математические олимпиады», в книгах Г. Штейнгауза («Математический калейдоскоп» и «Сто задач»), в книге Ф. Ф. Нагибина и Е. С. Кузьмина «Математическая шкатулка», в весьма веселой книге «Физики все еще шутят», а также в еженедельнике «Компьютерра» (#25 от 23 июня 1997 г.)
Некоторые формулы были выведены самостоятельно автором.
Я выражаю свою искреннюю благодарность Константину Кнопу («Компьютерра») за интересное содержательное общение, идеи, исправления ошибок.
Я выражаю свою искреннюю благодарность Дмитрию Новикову за добавление новых числовых соотношений и исправление ошибок.
Я выражаю свою искреннюю благодарность Алексею Федотову за добавление новых числовых соотношений и исправление ошибок.
Я благодарен Егору Быковскому за добавление в коллекцию четных и нечетных дат.
Числа и даты
Число 13452
Число 13452 образовано из пяти последовательных цифр (расположенных не по порядку) так, что число образованное первыми двумя цифрами, умноженное на среднюю цифру, дает число, образованное последними двумя цифрами.
Число 947658
Число 947658 образовано из шести последовательных цифр (расположенных не по порядку) так, что число образованное первыми двумя цифрами, умноженное на среднюю цифру, дает число, образованное последними тремя цифрами.
Числа 39157 и 57139
Данные числа составлены из пяти первых нечетных чисел 1, 3, 5, 7 и 9 следующим образом: произведение числа, образованного из первых двух цифр, на число, образованное двумя последними цифрами, минус число стоящее в середине равно числу, составленному из повторений одной и той же цифры.
Число 1444
Число 273863
Наибольшее число, которое при умножении на 365 дает число, содержащее восемь цифр, из которых первые четыре дважды повторяются.
272863 х 365 = 99959995
Аналогичные примеры есть
64253 х 365 = 23452345,
Легкое деление: чтобы разделить, просто перенесите первую цифру в конец
Частное, получающееся при перестановке в конец первой цифры делимого, можно найти для любого делителя и любой. Ниже два примера.
Число 8101265822784
Чтобы разделить 8 101 265 822 784 на 8, достаточно переставить первую цифру числа в конец.
8 101 265 822 784 : 8 = 1 012 658 227 848
Число 7101449275362318840579
Чтобы разделить 7 101 449 275 362 318 840 579 на 7, достаточно переставить первую цифру числа в конец.
7 101 449 275 362 318 840 579 : 7 = 1 014 492 753 623 188 405 797
Легкое деление (вариант 2): чтобы разделить, просто переставьте последнюю цифру в начало
В отличие от предыдущего случая, в данном варианте решение существует не всегда. Так, например, для делителя 2 решения не существует. Однако не все так плохо.
Числа 857142 и 428571
Чтобы разделить 857142 или 428571 на 3, достаточно переставить последнюю цифру каждого из чисел в начало.
857 142 : 3 = 285 714. 428 571 : 3 = 142 857
Цифровые совпадения
Произведение и сумма некоторых чисел дает в результате числа, состоящие из одинаковых цифр:
9 х 9 = 81 18 = 9 + 9;
2 х 47 = 94 49 = 2 + 47;
3 х 24 = 72 27 = 3 + 24;
2 х 497 = 994 499 = 2 + 497;
2 х 263 = 526 265 = 2 + 263.
Вообще, вводя девятки после первой цифры чисел из двух последних примеров, можно получить минимум два аналогичных результата при любом желаемом числе цифр:
2 х 4997 = 9994 4999 = 2 + 4997;
2 х 2963 = 5926 2965 = 2 + 2963.
Квадраты-палиндромы
264 2 = 69 696, а 2285 2 = 5 221 225
Во всех приведенных выше примерах число цифр квадрата было нечетным. Квадрат числа 836, равный 698 896, содержит четное число цифр. Среди всех квадратов, содержащих данное четное число цифр, палиндромический квадрат наименьший.
Число 1234567890
Число 1 234 567 890 разлагается на множители следующим образом:
1 234 567 890 = 2 х 3 х 3 х 5 х 3607 х 3803
Задача о десяти цифрах
Существует четыре числа, составленных из всех десяти цифр, таким образом, что эти числа делятся на все числа от 2 до 18:
2 438 195 760;
3 785 942 160;
4 753 869 120;
4 876 391 520.
Число 3333377733
Извлечение кубического корня
Иногда, чтобы извлечь кубический корень из числа, достаточно посчитать сумму цифр этого числа. Ниже приведены все такие числа:
Три различные цифры
Числа, составленные из трех различных цифр, каждое из которых делится на квадрат суммы своих цифр:
В обратном порядке
Произведение чисел 123 456 789 и 989 010 989 равно 122 100 120 987 654 321. Что интересно, в девяти младших разрядах полученного числа стоят цифры 9, 8, 7, 6, 5, 4, 3, 2, 1 (именно в таком порядке).
Арифметическая прогрессия
Существует как минимум четыре способа проделать вышеописанную операцию, чтобы в каждом случае три числа образовывали арифметическую прогрессию, а среднее число оставалось одним и тем же:
297 564 831;
291 564 837;
237 564 891;
231 564 897,
где разность равна соответственно 267, 273, 327 и 333.
В. Тебо в книге «Parmi les Nombers Curieux» показал, что существует 760 таких прогрессий. Кроме числа 456 (и его перестановок), среднее число может быть любой перестановкой следующих групп их трех цифр: 258, 267, 348 и 357.
Число 201599999798400
Число 201 599 999 798 400 представляет из себя сумму всех чисел, которые можно составить из девяти цифр (0 исключен), используя каждую цифру в каждом числе один и только один раз.
Число 1026753849
1 026 753 849 = 32 043 2
Число 9814072356
9 814 072 356 = 99 066 2
Числа 567 и 854
Данные числа и только они содержат вместе со своими квадратами по одному и только одному разу каждую из девяти цифр, исключая нуль.
567 2 = 321 489;
854 2 = 729 316.
Число 207
Используя каждую из девяти цифр, исключая нуль, один и только один раз, составим простые числа таким образом, что сумма этих чисел была минимальной. Эта сумма равна 207.
207 = 2 + 3 + 5 + 47 + 61 + 89
Девять цифр до и после знака равенства
Если 32 547 891 умножить на 6 (таким образом, в данной операции использованы все девять цифр от 1 до 9), то получится произведение, равное 195 287 346, также содержащее девять цифр по одному разу. Еще примеры такого рода:
94 857 312 х 6 = 569 143 872;
89 745 321 х 6 = 538 471 926;
98 745 231 х 6 = 592 471 386.
Сложение и умножение дает одинаковый результат
Существуют пары чисел, которые при сложении и умножении дают одинаковый результат, например: 1,1 и 11.
1,1 + 11 = 1,1 х 11 = 12,1
Впрочем, подобных чисел бесконечно много:
2 + 2 = 2 х 2 = 4;
6 + 1,2 = 6 х 1,2 = 7,2;
26 + 1,04 = 26 х 1,04 = 27,04.
Квадраты и кубы
Числа, равные сумме кубов своих цифр
Существуют четыре числа, если не считать 1, совпадающие с суммой кубов своих цифр:
153 = 1 + 125 + 27;
370 = 27 + 343;
371 = 27 + 343 + 1;
407 = 64 + 343.
Составные квадраты
Существует только два трехзначных квадрата (без нулей), которые, будучи выписанными подряд, образуют шестизначное число, в свою очередь представляющее собой квадрат:
225 = 15 2 и 625 = 25 2
225 625 = 475 2
Число 2519
Число 2519 таково, что если разделить его на 2, то в остатке получится 1; если разделить на 3, то в остатке получится 2; если разделить на 4, то в остатке получится 3; если разделить на 5, то в остатке получится 4; если разделить на 6, то в остатке получится 5; если разделить на 7, то в остатке получится 6; если разделить на 8, то в остатке получится 7; если разделить на 9, то в остатке получится 8; если разделить на 10, то в остатке получится 9:
2519 = 1259 х 2 + 1;
2519 = 839 х 3 + 2;
2519 = 629 х 4 + 3;
2519 = 503 х 5 + 4;
2519 = 419 х 6 + 5;
2519 = 359 х 7 + 6;
2519 = 314 х 8 + 7;
2519 = 279 х 9 + 8;
2519 = 251 х 10 + 9.
Двойная последовательность
для n = 4 имеем: 4, 2, 3, 2, 4, 3, 1, 1;
для n = 5 имеем: 3, 5, 2, 3, 2, 4, 5, 1, 1, 4;
для n = 8 имеем: 8, 6, 4, 2, 7, 2, 4, 6, 8, 3, 5, 7, 3, 1, 1, 5.
Такая последовательность не существует, если остаток числа n при делении на 4 равен 2 или 3.
a b и b a
Однако потребуется некоторые усилия, чтобы доказать, что
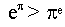
Число 40500000001
Сумма всех цифр, используемых при записи всех чисел, первое из которых единица, а последнее миллиард, составляет 40 500 000 001.
Простые числа и арифметическая прогрессия
Существуют арифметические прогрессии, где несколько последовательных членов прогрессии являются к тому же еще и простыми числами. Например, 10 последовательных членов арифметической прогрессии
являются простыми числами, так же как и 13 членов
все являются простыми числами.
Если рассматривать арифметические прогрессии с разностью 6, единственный случай, когда в такой прогрессии пять последовательных чисел:
Можно также доказать, что в любой арифметической прогрессии из натуральных чисел с разностью, меньшей 2000, не может находиться 12 последовательных простых чисел.
Числа 49, 4489, 444889, 44448889 и т.д.
Каждый член последовательности
является точным квадратом.
Число 4 и система неравенств
При этом x может принимать любое значение между 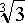
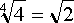
Всегда квадрат
Любопытное свойство числа 3
Группировка натуральных чисел
Предположим, что натуральные числа разделены на группы следующим образом:
Необыкновенное свойство комплексных чисел
Можно обобщить этот факт на более общий случай. При указанном выборе чисел x, y и z равенство