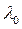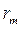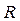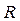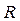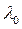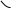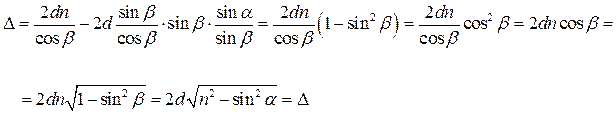что такое полосы равной толщины полосы равного наклона и равной толщины

Полосы равной толщины и равного наклона

Вы будете перенаправлены на Автор24

Полосы равной толщины

Координаты минимумов интерференции можно найти, зная, что:

Полосы такого типа можно наблюдать на самой пленке. Полоса следует за равной толщиной пленки, отсюда и название «полосы равной толщины».

Полосы равного наклона

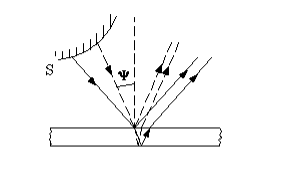
Тонкая пластинка (пленка) является плоскопараллельной (имеет одинаковую толщину). На эту пленку попадают лучи под разными углами наклона (рис.2). В таком случае разность хода интерферирующих волн зависит от угла падения лучей. Соответственно минимумы и максимумы интерференции следуют за углами, под которыми падают лучи. Для наблюдения картины интерференции следует собрать отраженные параллельные лучи. Следовательно, зрительный прибор надо сфокусировать на бесконечность. Поэтому считают, что полосы равного наклона наблюдаются на бесконечности. На практике интерференцию в плоскопараллельных пластинах наблюдают, располагая на пути отраженных лучей собирающую линзу. Экран при этом располагают в фокальной плоскости линзы.

Готовые работы на аналогичную тему

Условие максимума интенсивности для этой пленки имеет вид:

Решение:

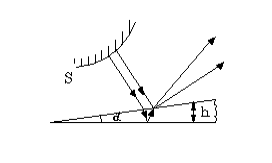
Для ситуации, описанной в задаче, ориентируясь на рис.1 можно записать, что:

Иначе оптическую разность хода лучей можно выразить:

\[\triangle =\left[2\left(m+1\right)+1\right]\frac<\lambda ><2>-\left[2m+1\right]\frac<\lambda ><2>=\lambda \ \left(m=0,1,2\dots \right)(1.3).\]

Приравняем правые части выражений (1.2) и (1.3):

Из уравнения (1.4) выразим h, получим:

Подставим выражение для h в формулу (1.1), найдем искомый угол:

Решение:

Запишем условие максимумов при интерференции:

\[\triangle =m\lambda \ при\ m=0,1,2\dots \left(2.1\right).\]

Для того чтобы найти выражение для разности хода складывающихся при интерференции лучей обратимся к рис. 3.

Из рис. 3, учитывая потерю половины волны при отражении света от оптически более плотной среды можно записать:

Из того же рис. 3 имеем:

Подставим полученные выражения в (2.3), (2.4) в формулу (2.2):

В соответствии с законом преломления можно записать:

Выразим искомую величину из выражения (2.8), получим:

Окончательно для минимальной толщины пленки имеем:

Источник

4. Полосы равной толщины и равного наклона.

Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от верхней и нижней границ тонкой воздушной прослойки, образованной поверхностями, соприкасающихся друг с другом толстой плоскопараллельной стеклянной пластинки и плосковыпуклой линзы с большим радиусом кривизны (рис. 32.4).

Б ольшой радиус кривизны линзы делает поверхности пластинки и линзы,

обращенные друг к другу практически параллельными. Тем более, что

интерференция происходит в области, близкой к точке касания пластинки и линзы (на рис. 32.4 лучи показаны для удобства восприятия далеко в стороне от этой области).

Луч 1, падающий на поверхность прослойки делится на два луча. Лучи 2 и 3

являются когерентными при малой толщине прослойки h (длина когерентности 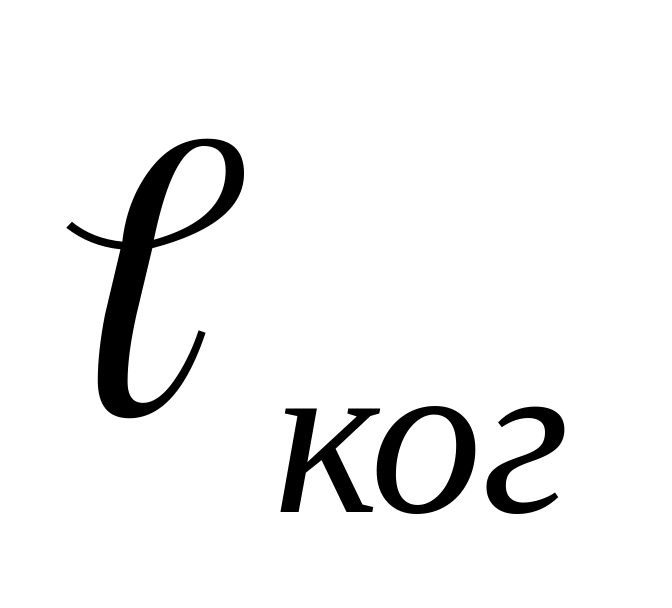должна быть больше 2h), поэтому при их сложении будет иметь место интерференция. Поскольку интерференция наблюдается в малой области вблизи точки касания О линзы и плоской стеклянной пластинки, поверхности линзы и пластинки здесь можно считать параллельными, а падающий и отраженный лучи (1, 2, 3) направленными вдоль одной прямой.

На радиусе r вдоль окружности толщина прослойки h будет одинаковой, и в этом случае наблюдаются интерференционные полосы равной толщины, имеющие форму колец с центром в точке касания линзы О. Эта интерференционная картина была впервые описана в 1675 г. Ньютоном и называется кольцами Ньютона.

Из рисунка 32.4 видно, что оптическая разность хода интерферирующих волн 2 и 3 Δ = 2hn +λ /2.

Коэффициент преломления воздуха n = 1. Слагаемое λ /2 возникает из-за того, что при отражении от оптически более плотной среды волны 3 (от стекла) оптический ход волны скачком увеличивается на λ /2. В том месте воздушного зазора, где выполняется условие

Δ = 2d + λ /2 = mλ (условие максимума),

наблюдаются светлые кольца, а там, где

Δ = 2d + λ /2 = (2m + 1) λ /2 (условие минимума),

возникают темные кольца. В месте соприкосновения линзы с плоскостью

пластины толщина воздушной прослойки практически равна нулю, поэтому разность хода стремится к λ /2, выполняется условие минимума, поэтому в центре интерференционной картины темное пятно (рис. 32.5). Интерференционные полосы имеют

вид концентрических колец. Таким образом, полосы равной толщины – это интерференционные полосы, возникающие в результате интерференции когерентных волн от мест с одинаковой толщиной.

Полосы равного наклона – интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами.

Рассмотрим оптическую схему на рис. 32.6. Почти монохроматический

свет лазера попадает на рассеивающую линзу, вмонтированную в экран. Расходящийся пучок света частично отражается от передней поверхности плоскопараллельной стеклянной пластины и, попадает на экран (1— 1΄), частично преломляется в пластине и, отражаясь от

задней поверхности пластины, снова преломляясь, попадает на экран (2-2΄). Если длина когерентности >>2hn, где h – толщина пластины, а n – показатель преломления, то волны пучка, сходящиеся в некоторой точке экрана. например т. А, будут интерферировать. На схеме рис. 32.6 это волны, соответствующие лучам 1 и 2. Поскольку расходящийся от линзы пучок является коническим, то интерференционные полосы будут иметь вид окружностей. А так как интерференционные максимумы (а также минимумы) будут располагаться в местах, соответствующих одинаковому углу падения лучей (одинаковому наклону их к поверхности), то получающаяся картина называется полосами равного наклона.

Источник

Полосы равной толщины и равного наклона.

Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от верхней и нижней границ тонкой воздушной прослойки, образованной поверхностями, соприкасающихся друг с другом толстой плоскопараллельной стеклянной пластинки и плосковыпуклой линзы с большим радиусом кривизны (рис. 32.4).

Большой радиус кривизны линзы делает поверхности пластинки и линзы,

обращенные друг к другу практически параллельными. Тем более, что

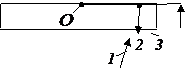являются когерентными при малой толщине прослойки h (длина когерентности 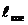должна быть больше 2h), поэтому при их сложении будет иметь место интерференция. Поскольку интерференция наблюдается в малой области вблизи точки касания О линзы и плоской стеклянной пластинки, поверхности линзы и пластинки здесь можно считать параллельными, а падающий и отраженный лучи (1, 2, 3) направленными вдоль одной прямой.

На радиусе r вдоль окружности толщина прослойки h будет одинаковой, и в этом случае наблюдаются интерференционные полосы равной толщины, имеющие форму колец с центром в точке касания линзы О. Эта интерференционная картина была впервые описана в 1675 г. Ньютоном и называется кольцами Ньютона.

Из рисунка 32.4 видно, что оптическая разность хода интерферирующих волн 2 и 3 Δ = 2hn +λ /2.

Коэффициент преломления воздуха n = 1. Слагаемое λ /2 возникает из-за того, что при отражении от оптически более плотной среды волны 3 (от стекла) оптический ход волны скачком увеличивается на λ /2. В том месте воздушного зазора, где выполняется условие

Δ = 2d + λ /2 = mλ (условие максимума),

наблюдаются светлые кольца, а там, где

Δ = 2d + λ /2 = (2m + 1) λ /2 (условие минимума),

возникают темные кольца. В месте соприкосновения линзы с плоскостью

вид концентрических колец. Таким образом, полосы равной толщины – это интерференционные полосы, возникающие в результате интерференции когерентных волн от мест с одинаковой толщиной.

Полосы равного наклона – интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами.

Рассмотрим оптическую схему на рис. 32.6. Почти монохроматический

задней поверхности пластины, снова преломляясь, попадает на экран (2-2΄). Если длина когерентности 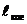>>2hn, где h – толщина пластины, а n – показатель преломления, то волны пучка, сходящиеся в некоторой точке экрана. например т. А, будут интерферировать. На схеме рис. 32.6 это волны, соответствующие лучам 1 и 2. Поскольку расходящийся от линзы пучок является коническим, то интерференционные полосы будут иметь вид окружностей. А так как интерференционные максимумы (а также минимумы) будут располагаться в местах, соответствующих одинаковому углу падения лучей (одинаковому наклону их к поверхности), то получающаяся картина называется полосами равного наклона.

Вопросы для самоконтроля.

1. В чем состоит явление интерференции?

2. Что такое когерентность?

3. В чем состоит временная когерентность?

Каков смысл времени и длины когерентности?

4. В чем состоит пространственная когерентность?

Каков смысл радиуса когерентности?

5. Что называется оптической длиной пути

и оптической разностью хода?

6. Каковы условия получения интерференционных максимумов и мини-

мумов при положении света от двух когерентных источников?

7. Как получаются полосы равной толщины и равного наклона?

ДИФРАКЦИЯ СВЕТА

1. Дифракция света. Принцип Гюйгенса-Френеля. Дифракция Френеля и Фраунгофера. Метод зон Френеля. Прямолинейное распространение света. Дифракция Френеля на круглом отверстии и диске.

2. Дифракция Фраунгофера на одной щели.

3. Дифракция Фраунгофера на одномерной дифракционной решетке. Многолучевая интерференция*.

Источник

Интерференция в тонких пленках. Полосы равного наклона и полосы равной толщины. Кольца Ньютона.

Наиболее типичным и распространенным примером интерференции света в природе является интерференция в тонких пленках (мыльные пузыри, радужная пленка нефти на воде и т.д.).

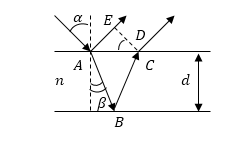
Пусть на прозрачную тонкую пластинку толщиной d падает плоская световая волна под углом a (рис. 6.1.7).

Разность хода, приобретенная лучами 1 и 2 до того, как они сойдутся в точке С, будет равна:

, где S₁=ВС; S₂=АО+ОС.

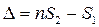
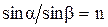
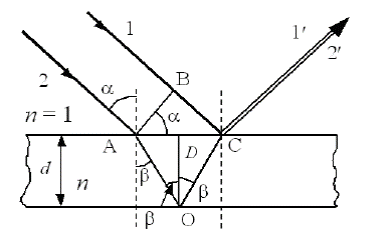
Воспользовавшись приведенными равенствами и соотношением (закон преломления света), получим, что:

Рис. 6.1.7. К выводу оптической разности хода при интерференции света

в плоскопараллельной пластине

Для получения окончательной разности хода необходимо учесть, что световые волны, как и всякие другие волны, отражаясь от оптически более плотнойсреды (луч 1 в точке С) получают дополнительную разность фаз, равную p, т.е. возникает добавочная разность хода, равная l/2. При отражении от среды оптически менее плотной (точка О) скачка фазы не происходит.

Таким образом, при падении на пластинку плоской волны образуются две отраженные волны, разность хода которых определяется формулой:

. (6.1.13)

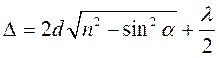
Если лучи 1 и 2 когерентны, то в отраженном и проходящем свете на экране получаются чередующиеся темные и светлые полосы (в случае монохроматического света) и цветные полосы (в случае белого света).

Практически интерференцию от плоскопараллельной пластинки наблюдают, поставив на пути отраженных пучков линзу, которая собирает лучи в одной из точек экрана, расположенного в фокальной плоскости линзы (рис. 6.1.8).

Рис. 6.1.8. Образование интерференционных полос равного наклона

Освещенность в точках экрана зависит от значения величины разности хода лучей, приходящих в эту точку.

При 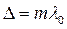пол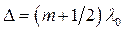учаются максимумы интенсивности.

При — минимумы интенсивности.

Если мы осветим пластинку рассеянным монохроматическим светом, то получим следующую картину. В рассеянном свете имеются лучи самых разнообразных направлений.

Лучи, параллельные плоскости рисунка и падающие на пластинку под углом α, после отражения от обеих поверхностей пластинки соберутся линзой в точке P₁ и создадут в этой точке освещенность, определяемую значением оптической разности хода. Лучи, идущие в других плоскостях, но падающие на пластинку под таким же углом, соберутся линзой в других точках, отстоящих от центра экрана на такое же расстояние, как и точка P₁.

Освещенность во всех этих точках будет одинакова. Таким образом, лучи падающие на пластинку под одинаковым углом, создадут на экране одинаково освещенные точки, расположенные по окружности с центром в О.

Лучи, падающие под другим углом, создадут на экране совокупность одинаково освещенных точек (значение освещенности зависит от угла падения лучей, т.к. он влияет на величину оптической разности хода 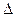), расположенных по окружности другого радиуса.

В результате на экране будет наблюдаться система чередующихся светлых и темных полос с общим центром в точке О.

Каждая полоса образована лучами, падающими на пластинку под одинаковым углом.Поэтому получающиеся в этих условиях интерференционные полосы носят название полос равного наклона.

Положение максимумов интенсивности зависит от длины волны света. Поэтому в белом свете получается совокупность смещенных друг относительно друга полос, образованных лучами разных цветов, и интерференционная картина приобретает радужную окраску

Возможность наблюдения интерференционной картины в белом свете определяется способностью глаза различать оттенки света близких длин волн. Лучи, отличающиеся по длине волны более чем на 20 Å, средний глаз уже может различить по цвету (поэтому мы с вами и брали ).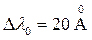

Рассмотрим образование интерференционных полос равной толщины.

Этот тип интерференции можно наблюдать если:

1) взять пластинку в виде клина с углом при вершине j (рис. 6.1.9);

2) положить одну плоскопараллельную стеклянную пластинку на другую, а под один из концов верхней пластины положить небольшой предмет так, чтобы между ними образовался воздушный клин.

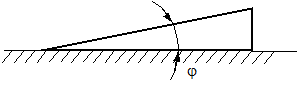Рис. 6.1.9. Интерференция в клине (пленке переменной толщины)

При малом угле j разность хода лучей можно с достаточной степенью точности вычислить по формуле: 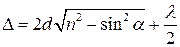, взяв в качестве d толщину пластинки в месте падения на нее лучей. Поскольку разность хода для лучей, отразившихся от различных участков клина, теперь неодинакова, освещенность экрана будет неравномерной, на экране появятся светлые и темные полосы. Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, вследствие чего их называют полосами равной толщины.

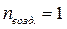
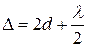
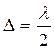
Если луч падает на воздушный клин нормально (sina=0) и , следовательно . В вершине клина d=0, поэтому . Значит, здесь будет наблюдаться темная полоса (минимум).

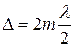
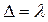
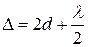
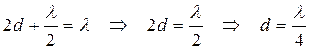
Первая светлая полоса (максимум) будет при (m=1) или , но . Приравниваем и получаем

.

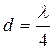
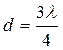
Следовательно, толщина воздушного клина в этом месте (в месте максимума) будет равна . Вторая светлая полоса будет находиться там, где толщина воздушного клина равна .

Полосы равной толщины могут быть прямыми линиями, концентрическими окружностями и любой другой формы в зависимости от расположения точек, соответствующих d=const. Угол клина должен быть очень мал, иначе полосы равной толщины будут накладываться друг на друга и их нельзя будет различить.

Сопоставим два рассмотренных случая интерференции при отражении от тонких пленок. Полосы равного наклона получаются при освещении пластинки постоянной толщины (d=const) рассеянным светом, в котором содержатся лучи различных направлений (a изменяется в широких пределах). Локализованы полосы равного наклона в бесконечности. Полосы равной толщины наблюдаются при освещении пластинки непостоянной толщины (d=var) параллельным пучком света (a=const). Локализованы полосы равной толщины вблизи пластинки.

В реальных условиях, например, при наблюдении радужных цветов на мыльной или масляной пленке, изменяется как угол падения лучей, так и толщина пленки. В этом случае наблюдаются полосы смешанного типа.

Дополнение:

Для клина: чем больше угол клина j, тем быстрее изменяется разность хода лучей вдоль клина, и тем чаще будут расположены интерференционные полосы.

При использовании белого света интерференционные полосы несколько расширяются, приобретая радужную окраску. Это объясняется зависимостью разности хода от длины волны l: в каждой светлой полосе максимумы для различных длин волн располагаются раздельно (то же самое происходит для различных длин волн в каждой темной полосе).

Один из первых экспериментов по наблюдению интерференции света в лабораторных условиях принадлежит И. Ньютону. Он наблюдал интерференционную картину, возникающую при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и лежащей на этой пластине плосковыпуклой линзой большого радиуса кривизны. Это является примером интерференции в тонких пленках (полосы равного наклона). Интерференционная картина имела вид концентрических колец (рис. 6.1.10), получивших название кольца Ньютона. Размеры колец зависят от длины волны применяемого света.

Рассмотрим, как возникает интерференционная картина в случае колец Ньютона (рис. 6.1.11). Пусть на линзу нормально к поверхности падает пучок монохроматических световых волн.

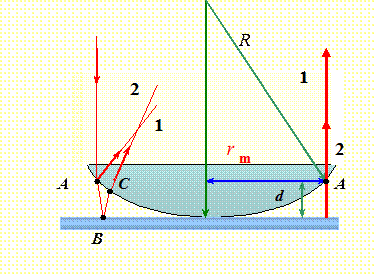
Рис. 6.1.11. Схема для наблюдения колец Ньютона.

Рассмотрим пучок, падающий в левой части линзы. Часть пучка, пройдя линзу и отразившись от поверхности раздела «линза – воздушная прослойка» в точке А, пойдет в направлении 1 (его отклонение для наглядности увеличено). Другая часть пучка, пройдя линзу, воздушную прослойку АВ и отразившись от стеклянной пластинки в точке В, пойдет по пути 2. На левой части рисунка лучи 1 и 2 для наглядности изображены условно. При большом радиусе кривизны линзы направление распространения лучей незначительно отклоняется от направления падающего луча, а точка их встречи стремится к точке A (правая часть рисунка). Направления отраженных лучей будут почти совпадать. Совпадение будет тем лучше, чем больше радиус линзы 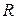. 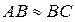Если радиус линзы велик, можно считать, что . Будут лучи 1 и 2 усиливать или ослаблять друг друга в точке наложения зависит от оптической разности хода этих лучей.

В рассматриваемом случае среда между линзой и пластинкой – воздух, а для воздуха 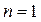. Тогда оптическая разность хода лучей 1 и 2 будет равна AB + BC »2d.

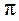
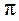
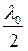
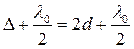
Необходимо также учесть, что фаза отраженных от оптически более плотной среды волн изменяется на . Оптически более плотной является та среда, абсолютный показатель преломления которой имеет большее значение. Первый луч отражается в точке A от оптически менее плотной среды (граница раздела линза – воздушная прослойка) и, следовательно, его фаза не меняется. Второй луч проходит воздушную прослойку AB и отражается в точке B от оптически более плотной среды (стеклянной пластинки), следовательно, его фаза изменяется на (волна сдвигается на ). Добавим ее к оптической разности хода:

.

Так как расстояние от линзы до пластинки 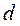одинаково для всех точек находящихся на одном и том же расстоянии от центра линзы, то наблюдаемая картина интерференции будет представлять собой чередование темных и светлых колец.

Рассмотрим темные кольца. Условие интерференционного минимума:

, где . Отсюда .

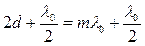
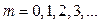
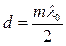
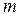
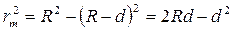
Найдем чему равен радиус -го темного кольца Ньютона. По теореме Пифагора (рис. 6.1.11) можно записать:

.

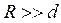
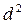
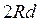
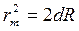
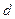
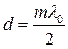
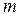
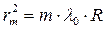
Учитывая, что , можно пренебречь величиной по сравнению с . Тогда получим: . Подставив выражение для ( ), получим величину квадрата радиуса -го темного кольца

. (6.1.14)

Таким образом, если известна длина световой волны , которой освещается пластинка с линзой и измерен радиус темного кольца, можно определить радиус кривизны линзы . Такой способ особенно удобен при больших значениях . Очевидно, что если мы знаем радиус кривизны линзы , можно определить длину световой волны , которой освещается пластинка с линзой.

Источник