что такое группы чисел
Группа (математика)
Существуют математические объекты не являющиеся числами, но над ними мы имеем возможность совершать алгебраические действия. Свойства этих действий напоминают свойства действий над числами. Это делает необходимой сформулировать более общие понятия.
Определение 1. Полугруппой называется множество, в котором определено действие, сопоставляющее каждой упорядоченной паре элементов этого множества третий элемент − результат действия. Предполагается, что действие ассоциативно, т.е.
где ○− знак действия.
Если операция коммутативна, т.е.
Рассмотрим примеры групп:
1. Множество всех целых чисел относительно сложения.
Действительно, операция сложения ассоциативна (a+b)+c=a+(b+c). Нейтральным элементом является 0 (a+0=0+a=a). Наконец, обратным для элемента а является −a ( a+(−a)=(−a)+a=0).
2. Множество положительных рациональных чисел относительно умножения.
Покажем, что это множество удовлетворяет всем трем пунктам определения 2. Ассоциативность очевидна ( (ab)c=a(bc) ). Нейтральным элементом является 1 ( a·1=1·a=a ).И, наконец, обратным элементом для a является 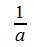
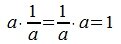
3. Множество квадратных матриц относительно сложения.
Ассоциативность сложения очевидно следует из правил сложения матриц (a+b)+c=a+(b+c). Нейтральным элементом является нулевая матрица, а обратным (противоположным) элементом является нулевая матрица.
Все вышеизложенные примеры групп являются также коммутативными. Приведем пример некоммутативной группы.
4. Множество квадратных невырожденных матриц относительно умножения.
Действительно. Ассоциативность умножения матриц сохраняется. Нейтральным элементом является единичная матрица. Единичная матрица является невырожденной, умножение невырожденных матриц будет невырожденным, следовательно всегда существует обратная матрица. При множестве матриц порядка n≥2 мы имеем дело с некоммутативной группой т.к. умножение матриц в общем случае некоммутативна ab≠ba.
Разряды и классы чисел
Числа и цифры
Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.
Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.
Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определенное место — позицию.
Классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.
Названия классов многозначных чисел справа налево:
Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
А теперь прочитаем число единиц каждого класса слева направо:
Разряды чисел
От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.
Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще чтобы визуально разделить классы чисел.
Разрядные единицы обозначают так:
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Чтобы легче понимать математику — записывайтесь на наши онлайн-курсы по математике!
Потренируемся
Пример 1. Записать цифрами число, в котором содержится:
Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отброс ить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.
Пример 2. Сколько сотен содержится в числе 6284?
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.
Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.
Значит, в данном числе содержится 62 сотни.
Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.
Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.
Группы, кольца, поля в математике
Группа: определение и примеры групп
Множество с алгебраической операцией называется группой, если выполняются следующие условия:
1) операция в ассоциативна: ;
2) в существует нейтральный элемент ;
Решение. Действительно, операция умножения определена на указанном множестве, так как
Кольцо
1) относительно операции сложения множество — коммутативная группа, т.е.
а) операция сложения коммутативна: ;
б) операция сложения ассоциативна: ;
в) существует нулевой элемент ;
г) для каждого элемента существует противоположный ему элемент ;
2) операция умножения в множестве ассоциативна:
3) операции сложения и умножения связаны законами дистрибутивности:
Кольцами являются множества целых, рациональных, действительных чисел, причем все они — коммутативные кольца с единицей. Примеры других колец, в том числе и некоммутативных, встретятся в дальнейшем. Как видим, кольцо — это множество, в котором определены три операции: сложение, умножение и вычитание.
Если операция коммутативна, то дистрибутивность слева операции относительно операции влечет дистрибутивность справа, так как
Решение. В самом деле, для любых положительных действительных чисел справедливы равенства
Следовательно, операция дистрибутивна справа относительно операции умножения чисел. Дистрибутивность слева относительно умножения опровергается примером
Пример В.7. Доказать, что множество чисел вида, где и — целые числа, является кольцом:
Решение. Действительно, операции сложения и умножения определены на рассматриваемом множестве, так как сумма и произведение двух чисел вида (В.2) имеют тоже самое представление:
Таким образом, рассматриваемое множество удовлетворяет всем условиям определения кольца.
Поле: определение и примеры полей
1) — коммутативное кольцо с единицей ;
Как видим, поле — это множество, в котором определены четыре операции: сложение, умножение, вычитание и деление. Полями, например, являются множества рациональных и действительных чисел.
Пример В.8. На множестве трех целых чисел определим две операции:
1) «сложение по модулю 3» — остаток от деления суммы на 3 (обозначим через );
2) «умножение по модулю 3» — остаток от деления произведения на 3 (обозначим через ).
Доказать, что множество является полем относительно введенных операций.
– остаток от деления на 3 суммы не изменится, если слагаемое (или не сколько слагаемых) заменить его остатком при делении на 3:
– остаток от деления на 3 произведения не изменится, если множитель (или несколько множителей) заменить его остатком при делении на 3:
Рассматриваемые в примере операции «сложения по модулю 3» и «умножения по модулю 3» можно представить в виде
Покажем, что множество является коммутативным кольцом с единицей. В самом деле, операция «сложения по модулю 3» коммутативна и ассоциативна. Это следует из коммутативности и ассоциативности сложения чисел. Действительно, из равенства следует, что
Коммутативность доказана. Заметим, впрочем, что коммутативность «сложения по модулю 3» видна непосредственно по таблице (см. рис.В.2): слагаемые и в таблице можно поменять местами, при этом таблица не изменится.
Из равенства следует, что
Ассоциативность «сложения по модулю 3» доказана.
Итак, множество относительно операции «сложения по модулю 3» является коммутативной группой.
Операция «умножение по модулю 3» ассоциативна и коммутативна, что следует из ассоциативности и коммутативности умножения целых чисел, а также свойств остатков:
Следовательно, операция «умножения по модулю 3» дистрибутивна слева относительно операции «сложения по модулю 3». Дистрибутивность справа можно не проверять, так как обе операции коммутативны.
Единичным элементом служит число 1 (что видно по таблице «умножения по модулю 3»). Следовательно, — коммутативное кольцо с единицей.
Пример В.9. Доказать, что множество чисел вида, где и — рациональные числа, является полем:
Решение. Действительно, операции сложения и умножения определены на рассматриваемом множестве, так как сумма и произведение двух чисел вида (В.З) имеют тоже самое представление:
Так как рассматриваемое множество является коммутативным кольцом с единицей и каждый элемент, отличный от нуля, имеет обратный, то оно является полем.
Разряды и классы чисел
Классы чисел
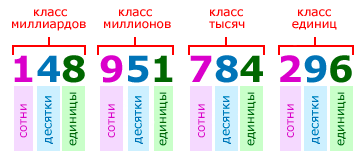
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса:
Названия классов многозначных чисел справа налево:
Для удобства чтения записи многозначного числа, между классами оставляется небольшой пробел. Например, чтобы прочитать число 148951784296, выделим в нём классы:
и прочитаем число единиц каждого класса слева направо:
148 миллиардов 951 миллион 784 тысячи 296.
Разряды чисел
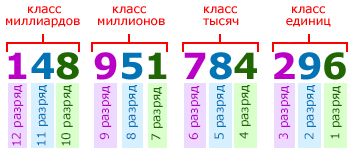
Каждая цифра в записи многозначного числа занимает определённое место — позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.
Счёт разрядов идёт справа налево. То есть, первая цифра справа в записи числа называется цифрой первого разряда, вторая цифра справа — цифрой второго разряда и т. д. Например, в первом классе числа 148 951 784 296, цифра 6 является цифрой первого разряда, 9 — цифра второго разряда, 2 — цифра третьего разряда:
Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами:
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Пример. Запишите цифрами число, которое содержит:
1) 37 единиц второго класса и 565 единиц первого класса;
2) 450 единиц второго класса и 9 единиц первого класса;
3) 8 единиц второго класса и 50 единиц первого класса.
Все разрядные единицы, кроме простых единиц, называются составными единицами. Так, десяток, сотня, тысяча и т. д. — составные единицы. Каждые 10 единиц любого разряда составляют одну единицу следующего (более высокого) разряда:
| 10 единиц | = | 1 десяток; |
| 10 десятков | = | 1 сотня; |
| 10 сотен | = | 1 тысяча; |
| 10 тысяч | = | 1 десяток тысяч; |
| 10 десятков тысяч | = | 1 сотня тысяч; |
| 10 сотен тысяч | = | 1 тысяча тысяч (1 миллион); |
Любая составная единица по сравнению с другой единицей, меньшей её называется единицей высшего разряда, а по сравнению с единицей, большей её, называется единицей низшего разряда. Например, сотня является единицей высшего разряда относительно десятка и единицей низшего разряда относительно тысячи.
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, надо отброс ить все цифры, означающие единицы низших разрядов и прочитать число, выражаемое оставшимися цифрами.
Например, требуется узнать, сколько всего сотен содержится в числе 6284, т. е. сколько сотен заключается в тысячах и в сотнях данного числа вместе.
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит в числе есть две простые сотни. Следующая влево цифра — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60. Всего, таким образом, в данном числе содержится 62 сотни.
Цифра 0 в каком-нибудь разряде означает отсутствие единиц в данном разряде.
Например, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
24 527 — двадцать четыре тысячи пятьсот двадцать семь.
Группа (алгебра)
Гру́ппа — в абстрактной алгебре непустое множество с определённой на нём бинарной операцией, удовлетворяющей указанным ниже аксиомам. Ветвь математики, занимающаяся группами, называется теорией групп.
Всем знакомые вещественные числа наделены сложением — операцией, обладающей некоторым набором свойств. Похожими свойствами обладают и многие другие из объектов, которые изучает математика, — например, множество вращений плоскости вокруг начала координат. Теория групп занимается изучением взаимосвязей между этими свойствами в общем виде. Структура группы включается в различные другие алгебраические структуры, такие как поля, векторные пространства или группы Ли. Кроме того, группы являются важными инструментами в изучении симметрии во всех её проявлениях.
Содержание
Определения
Комментарии
Связанные определения
Примеры
Стандартные обозначения
Мультипликативная запись
Обычно групповую операцию называют (абстрактным) умножением; тогда применяется мультипликативная запись:
Аддитивная запись
В коммутативной группе определяющяя операция часто рассматривается как (абстрактное) сложение и записывается аддитивно:
Простейшие свойства
Получение новых групп из уже известных
Обобщения
См. также
Популярная литература
Научная литература
Ссылки
Полезное
Смотреть что такое «Группа (алгебра)» в других словарях:
Алгебра Хопфа — Алгебра Хопфа алгебра, являющаяся унитарной ассоциативной коалгеброй и, таким образом, биалгеброй c антигомоморфизмом специального вида. Названа в честь Х. Хопфа. Алгебры Хопфа встречаются в алгебраической топологии, где они возникли в… … Википедия
ГРУППА — множество, на к ром определена операция, наз. умножением и удовлетворяющая спец. условиям (групповым аксиомам): в Г. существует единичный элемент; для каждого элемента Г. существует обратный; операция умножения ассоциативна. Понятие Г. возникло… … Физическая энциклопедия
Группа Ли — Группа (математика) Теория групп … Википедия
Группа Шрёдингера — Группа Шрёдингера это группа симметрии свободного уравнения Шрёдингера. Содержание 1 Алгебра Шрёдингера 2 Роль группы Шрёдингера в математической физике … Википедия
Группа Гейзенберга — группа, состоящая из квадратных матриц вида где элементы a, b, c принадлежат какому либо коммутативному кольцу с единицей. В качестве такого кольца R чаще всего берется: кольцо вещественных чисел так называемая непрерывная группа Гейзенберга,… … Википедия
Алгебра Темперли — Алгебра Темперли Либа, в статистической механике алгебра, при помощи которой строятся некоторые трансфер матрицы. Открыты Невиллом Темперли и Эллиотом Либом. Также алгебра применяется в теории интегрируемых моделей, имеет отношение… … Википедия
АЛГЕБРА МЕР — алгебра М(G).комплексных регулярных борелевских мер на локально компактной абелевой группе G, имеющих ограниченную вариацию, с обычными линейными операциями и сверткой в качестве умножения (см. Гармонический анализ абстрактный). Свертка полностью … Математическая энциклопедия
АЛГЕБРА С ДЕЛЕНИЕМ — алгебра Анад полем F, для любых элементов и bк рой уравнения разрешимы в А. Ассоциативная А. с д., рассматриваемая как кольцо, является телом, а ее центр С полем и Если то А. с д. Аназ. центральной А. с д. Конечномерные центральные ассоциативные… … Математическая энциклопедия
ГРУППА СУСЛОВИЕМ КОНЕЧНОСТИ — группа, элементы или подгруппы к рой удовлетворяют тому или иному условию конечности. Под условием конечности в теории групп понимается любое такое свойство, присущее всем конечным группам, что существуют бесконечные группы, к рые им не обладают … Математическая энциклопедия