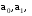что такое гипердействительные числа

Гипердействительные числа можно рассматривать как классы последовательностей обыкновенных действительных чисел. Рассмотрим способ построения классов. Его определение будет использовать так называемый нетривиальный ультрафильтр на множестве натуральных чисел. Объясним, что это такое.

Любое множество натуральных чисел является либо большим, либо малым. Ни одно множество не является большим и малым одновременно.

С помощью такого ультрафильтра построим искомое неархимедово расширение поля действительных чисел.

Определим сложение и умножение на гипердействительных числах. Пусть класс содержит последовательность , класс — последовательность . Назовем суммой классов и класс, содержащий последовательность ,а произведением последовательность . Корректность этих определений обеспечивается свойством 4 из определения ультрафильтра.

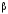
Итак, мы ввели на множестве гипердействительных чисел сложение, умножение и порядок. Нетрудно проверить, что мы получили упорядоченное поле, т.е. что в множестве гипердействительных чисел выполняются все обычные свойства сложения, умножения и порядка. Аксиома Архимеда, однако, в этом поле не выполняется.

ПОСТРОЕНИЕ ПОЛЯ ГИПЕРДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ С ПОМОЩЬЮ

Рассмотрим другой метод построения поля гипердействительных чисел. Но прежде мы должны обсудить понятие логического языка и понятие интерпретации этого языка. Рассмотрим общее понятие односортного языка первого порядка.

Пусть фиксирован набор символов , элементы которого мы будем называть предикатными символами, и набор , элементы которого мы будем называть функциональными символами. Пусть каждому предикатному и функциональному символу сопоставлено некоторое натуральное число, называемое числом аргументов, или валентностью, соответствующего символа. В таком случае говорят, что задан некоторый язык.

Определим теперь понятие формулы данного языка. Выберем и зафиксируем бесконечную последовательность символов, называемых переменными. Пусть это будут например символы Определим в начале понятие терма. Именно (Т1) любая переменная и любой функциональный символ с нулем аргументов суть термы;

Термами называются те и только те выражения, которые можно получить путем многократного применения правил (Т1) и (Т2). Определим теперь понятие формулы следующим образом:

Формулами называют те и только те выражения, которые можно получить путем многократного применения правил (Ф1)-(Ф4).

Определить интерпретацию языка L означает:

с каждым предикатным символом Р валентности m сопоставить некоторый m-местный предикат;

С каждым функциональным символом f валентности k сопоставить некоторую функцию F, ставящую в соответствие любой k-элементной последовательности элементов М некоторый элемент М:F:.

Истинность формул зависит от выбора интерпретации и от значений переменных, входящих в эту формулу свободно. Если формула не содержит свободных вхождений, то ее истинность зависит только от выбора интерпретации. Формулы языка, не содержащие свободных вхождений переменных, называют суждениями данного языка. Как только мы зафиксировали какую-то интерпретацию языка, все суждения разделяются на истинные и ложные.

Теперь мы в состоянии точно сказать, что мы называем гипердействительными числами. Именно, системой гипердействительных чисел называется любая интерпретация Р рассмотренного языка RL, в которой истинны те же суждения, что и в стандартной интерпретации, но для которой не выполнена аксиома Архимеда. Элементы носителя этой интерпретации и называются гипердействительными числами. Таким образом, возможно много систем гипердействительных чисел.

Вернемся к построению системы гипердействительных с помощью методов математической логики.

Введем еще один термин, относящийся к произвольному языку L и произвольному множеству Т суждений языка L.Назовем множество Т совместным, если существует его модель, т.е. если существует интерпретация языка L, в которой истинны все формулы из Т. Теперь все готово для того, чтобы сформулировать теорему компактности Мальцева.

Теорема компактности. Пусть имеется произвольный язык L и произвольное множество Т суждений этого языка. Пусть каждое конечное подмножество множества Т совместно. Тогда множество Т совместно.

Эта теорема показывает, что для построения модели множества Т достаточно уметь строить модели всех конечных подмножеств множества Т.

Свойство выводимости: если формула выводится из множества Т, то существует такое конечное подмножество , что формула выводится из множества . Наконец, назовем множество суждений противоречивым, если из него выводится одновременно некоторое суждение и его отрицание . Теперь сформулируем теорему Гёделя о полноте.

Источник

Большая Энциклопедия Нефти и Газа

Гипердействительное число

Гипердействительное число а, большее всех стандартных чисел, называется положительным бесконечно большим. Аналогично определяются отрицательные бесконечно большие числа. [1]

Любое конечное гипердействительное число бесконечно близко к некоторому стандартному числу. [3]

Два гипердействительных числа а / 3 называются бесконечно близкими, если их разность бесконечно мала. [5]

Наконец, гипердействительное число называется бесконечно малым, если его абсолютная величина меньше любого стандартного положительного числа. Согласно этому определению нуль тоже является бесконечно малым числом. Легко проверить, что ненулевое число е является бесконечно малым тогда и только тогда, когда 1 / е бесконечно велико. В самом деле, пусть, например, е 0 бесконечно мало. [6]

Покажите, что множество гипердействительных чисел разбивается на галактики. [8]

Покажите, что множество конечных гипердействительных чисел не является внутренним. [9]

Покажите, что два конечных гипердействительных числа бесконечно близки тогда и только тогда, когда между ними нельзя вставить двух разных стандартных чисел. [10]

Покажите, что для всякого гипердействительного числа существует большее его гипернатуральное. [11]

К каждому действительному числу поле гипердействительных чисел добавляет, как образно говорят, ореол из бесконечно малых чисел. [12]

Читатель должен заметить, что сумма Римана является конечным гипердействительным числом ; поэтому она имеет стандартную часть. [14]

Источник

Что такое гипердействительные числа

Мы публикуем старую, 2002 г., работу П.В. Полуяна, в которой он применил нестандартный анализ для описания различных физических процессов, а так же поставил задачу о связи гипердействительных и действительных чисел, в том числе с числами Фибоначчи.

В 1985 г. идея о применимости нестандартного анализа для описания целостности Вселенной и фундаментального материального уровня (через монады) была высказана в работе В.Ю. Татура и С.Ф. Кравченко «Естественнонаучные основы антропокосмизма». В последующие годы (1986-1988) для обозначения этого материального уровня было введено понятие «слабая метрика». Эта материальная субстанция является не только воплощением и носителем целостности, но и основой нашего мышления в понятиях.

В связи с этим, следует пояснить о каком я веду речь, и почему столь важны квантово-релятивистские характеристики объективного мира. Поэтому статья начнется с философского вступления, которое читатели не склонные к вопросам философии и методологии могут пропустить. После вступления материал статьи располагается так:

III. Деструкция линейного континуума временного порядка, хронометрика. Понятие ареального множества и приложение его к анализу времени. Множество нормировок.

IV. Бесконечные ряды как ареальные множества. Гипердействительность. Нестандартный подход к псевдоевклидовому континууму. Неархимедово сложение и скорость света. Обратная скорость как инвариант.

V. Некоторые общетеоретические выводы. Многообразие геометрий и единственность эмпирического пространства.

Ричард Фейнман в своей книге пишет: (Richard Feynman, The Character of Physical Law. Русский перевод: Р.Фейнман. Характер физических законов. М.: Мир, 1968, с. 184).

Прошу прощения за столь обширное цитирование, оно понадобилось, чтобы обосновать основные предпосылки важной проблемы:

1. Существует принципиальное расхождение между современными физическими представлениями о движении и классическими понятиями анализа.

Однако на самом деле речь надо вести не о МОДЕЛИ, и не о ПОСТРОЕНИИ. Задача в том, чтобы внутри самой логики классической математики найти основания для дальнейшего развития теории.

Правда, в последнем случае, мы можем обнаружить некоторые интересные особенности.

I. АКТУАЛЬНАЯ БЕСКОНЕЧНОСТЬ В СОБСТВЕННОМ СМЫСЛЕ СЛОВА

Критикуя Фонтенеля за поиски бесконечно больших чисел ВНУТРИ расходящегося числового ряда, Кантор сам помещает актуально бесконечно малые сходящегося ряда и успешно доказывает, что их там нет. Но ведь актуально бесконечно малые могут быть помещены ВНЕ числового ряда действительных чисел, и тогда приговор Кантора окажется несостоятельным. Характерно, что в примечаниях к цитируемому сборнику его трудов научный редактор Колмогоров А.Н. пишет: (Ук. изд. с. 408).

В принципе, единственным критерием остается способность данного подхода необходимым образом войти в систему науки. Канторовы трансфиниты открыли перед нами обширную область приложения творческих усилий, дают ли такую же возможность гипердействительные числа?

Давайте посмотрим, на какой идейный базис опирается традиционное представление о бесконечном делении непрерывного континуума.

Проблема становится еще острее, когда в положении недифференцируемого О оказываются все точки траектории. Рассмотрим фигуру Ван-дер-Вардена, получаемую из равностороннего треугольника, когда каждая сторона его делится на три части, к которым добавляется еще одна, образуя на каждой из сторон новый треугольник:

И наоборот, можно в действительной области построить ряд отрезков, соответствующих :

Попробуем интерпретировать данный результат.

II. ДВИЖЕНИЕ С НЕОПРЕДЕЛЕННОЙ СКОРОСТЬЮ.

Разумеется, можно развести реальное движение и его математическую модель, но поставив под сомнение адекватность последней, надо, по крайней мере, предложить иной способ теоретического моделирования. И при этом, все-таки, придется исходить из тех же самых элементарных предпосылок: любые виды механического движения суть перемещения точки в проcтранстве (она, грубо говоря, в разные моменты времени находится в разных местах), точки нахождения всегда разделены неким расстоянием, а моменты нахождений задают интервалы времени. Самое интересное, что эти же исходные предпосылки позволяют сформировать совершенно иное представление о движении, противоположное традиционному.

2. Если в любой момент в любой точке пути скорость одна и та же, она присуща материальной точке и в течение всего времени движения по всей траектории.

Очевидно, эти утверждения обосновывают друг друга, образуя логический круг.

Главная черта данной модели движения: ни в одной точке нет определенной скорости. Эта неопределенность заложена в модель: между сколь угодно близкими моментами времени всегда найдется мгновение, которому соответствуют новые нахождение точки в пространстве с новыми значениями скорости.

Так становится очевидной и причина альтернативности нашего построения: традиционное понимание основано на понятии отрезка (который и задает точки его ограничивающие), а наше, нетрадиционное понимание, наоборот, основывается на точках и моментах нахождений, любая пара которых задает отрезки-интервалы, обнаруживаемые между ними. Общим для обоих альтернативных вариантов остается то, что последовательность прохождения точек (нахождений в пространстве) сообразна последовательности мгновений времени, которые им соответствуют.

Наличие нестандартной модели анализа в современной математике свидетельствует, что никаких принципиальных, логических запретов на избранном нами пути не существует. Пусть новые представления о движении кажутся, если не абсурдными и безумными, то надуманными и бесполезными. Они, просто-напросто, необычны и непривычны, но точно также НЕПРОТИВОРЕЧИВЫ.

Тем не менее, мы попытаемся рассмотреть этот вопрос подробнее. Но прежде чем вести разговор о пространстве-времени, следует осмыслить важнейшую составляющую этого 4-х мерного континуума. Предметом нашего исследования будет ВРЕМЯ.

III. ХРОНОМЕТРИКА. АРЕАЛЬНЫЕ МНОЖЕСТВА.

Уитроу замечает: (Дж.Уитроу, Естественная философия времени, с. 207.)

Однако, как и следовало ожидать, в анализе проблемы конгруэнтности у Грюнбаума чаще всего рассматриваются пространственные отношения, которые потом переносятся на временной порядок. А специфика временного порядка опять-таки появляется только в анализе анизотропии (направленности) времени и экзотических вариантов замкнутого, циклического временного порядка.

Если мы абстрагируемся от субъективности, то ВРЕМЯ предстанет перед вами как предмет вполне пригодный для аналитики и мы заметим одну фундаментальную его особенность.

3. Элементам ЭТОГО множества будет приписано оригинальное качество: если один элемент этого множества ЕСТЬ, то остальных элементов этого множества НЕТ.

Что мы получили в результате такого определения?

Аристотель, а за ним и все логики, постоянно подчеркивали, формулируя закон противоречия: не может быть и А и не-А в одном и том же отношении, в одно и то же ВРЕМЯ. Сейчас важно переставить акценты: мы формулируем ЛОГИЧЕСКОЕ ОТНОШЕНИЕ, с помощью которого моделируем время, а не эмпирическое время используем для подкрепления логической очевидности.

Введя принцип АРЕАЛЬНОСТИ, мы неожиданно обнаруживаем в самом эмпирическом времени особое свойство.

Это уже следующий шаг в понимании времени, понятие ареальности приводит, как видим, к необходимости дальнейшего анализа, но здесь мы ограничимся сказанным. На данном этапе построения ХРОНОМЕТРИКИ элементарного качественного описания, полагаю, достаточно.

Чтобы хоть как-то обосновать свой подход, я должен уточнить исходную теоретическую позицию.

Сейчас мы попробуем понять КАК ЭТО ПРОИСХОДИТ, рассматривая конкретные случаи последовательностей. Возможно, наше рассмотрение будет выглядеть неким произвольным измышлением, но, если ЛОГИКА АРЕАЛЬНОСТИ принята, то эти выводы будут получаться с необходимостью. Однако прежде чем это сделать, следует кое-что уточнить.

Важным критерием научности подхода, является его способность давать выводы, позволяющие увидеть ранее не видимые связи между привычными явлениями и понятиями. Полагаю, что решающее слово здесь будет не за математиками, а за физиками.

IV. НЕСТАНДАРТНЫЙ ПОДХОД И РЕЛЯТИВИСТСКИЕ ИНВАРИАНТЫ

Сейчас мы обратимся к физике, я попробую продемонстрировать, как нестандартный подход позволяет связать области, между которыми ранее связь не прослеживалась.

В 4-х мерном псевдоевклидовом континууме реального пространства-времени периоды времени и отрезки пространства связаны коэффициентом пропорциональности, который в физике интерпретируется как скорость света умноженная на миную единицу. В классической физике верхний предел скорости был неограничен, теперь роль бесконечности стала исполнять скорость света. Иными словами, все забесконечные значения скорости оказались вытеснены в нереальность, а это наводит на определенные мысли. Что если попытаться применить здесь технику, уже опробованную нами на бесконечных последовательностях?

[Поскольку принцип относительности имеет и более замысловатые интерпретации, а это вызывает недопонимание (рецензент «Научной сети», например, счел мою трактовку ошибочной), привожу здесь цитату из работы Альберта Эйнштейна «Что такое теория относительности?»: «Координатная система, движущаяся равномерно и прямолинейно относительно инерциальной системы, сама является инерциальной. Специальный принцип относительности представляет собой обобщение этого утверждения на все процессы природы: каждый универсальный закон природы, который выполняется по отношению к некоторой системе отсчета С, должен также выполняться в любой другой системе С`, которая движется равномерно и прямолинейно относительно С». (А.Эйнштейн. Собрание научных трудов. т. I, М.: «Наука», 1965 с. 679.)]

Схематически принцип относительности поясняется на примере двух точек:

Что мы вообще хотим сказать, когда говорим: «Данная материальная точка имеет заданную скорость?»

Разве нас удивляет, что на стадионе спортивный результат судьи выражают не в численном значении скорости бегуна, а в количестве времени, затраченном на прохождение дистанции? Это ведь уникальный факт: движение измеряется не метрами за секунду, а временем, которое потребовалось для преодоления заданного расстояния! Тем не менее, в физике данная мера движения с размерностью [с/м] отвергается. Почему?

У Лейбница есть еще одно примечательное рассуждение: он отождествляет нулевую скорость движения по окружности с бесконечной скоростью, когда (Т. 3, с. 290). То есть логически отождествляются не только О м/с и [ с/м (соответственно [ м/с и О с/м), но также О м/с и [ м/с при циклическом движении. Это последнее отождествление открывает перед нами выход из запутанной ситуации.

Почему не удобно отсчитывать увеличение скорости движения в мере [с/м]? Потому, что приписывая системе отсчета бесконечную медленность и вводя для движущейся точки некую единичную медленность 1[с/м], мы не получим равномерную шкалу величин, где можно арифметически складывать А[с/м] + В[с/м] = (А + В)[с/м]. То есть такое сложение будет противоречить нормальному представлению о том, как оцениваются скорости числом переходов от одной системы отсчета к другой. Но дело коренным образом измениться, если мы воспользуемся, так сказать, преобразованием Лейбница.

Создав его, мы сталкиваемся с проблемой интерпретации, поскольку «обратная скорость света» имеет меру [с/м] и не может являться скоростью в обычном понимании этого слова. Эту странную величину на основе традиционного принципа относительности можно интерпретировать как «скорость» вращения по единичной орбите, а коэффициент 1/v для нового типа континуума оказывается константой, которой в физике соответствует комбинация констант e 2 /h. Вряд ли это является совпадением. Напротив, поскольку в математических построениях, относящихся к многомерному комплексному анализу, все величины безразмерны, а в физике они связаны с конкретными физическими параметрами, отмеченная двойственность псевдоевклидова континуума пространства-времени имеет нетривиальный смысл. По крайней мере, этот формальный подход показывает определенного рода взаимосвязь между понятиями и представлениями теории относительности и квантово-механическими параметрами.

Кроме математических аксиом и логики, есть еще некие также мировоззренческие принципы, главным из которых является принцип детерминизма: мы усматриваем связь между явлениями ТАК, как ОН того требует. То понимание детерминизма, которое ныне общепринято, привело, например, к своеобразным мировоззренческим выводам: в научном истеблишменте укрепилось мнение о близком завершении фундаментальной науки. Поскольку это мнение мне представляется одним из проявлений господствующей идеологии, а публикуемая работа направлена против нее, этому вопросу посвящена отдельная статья «Игра в шахматы и квантовая механика», с которой читатели, заинтересовавшиеся «Нестандартным анализом неклассического движения», также могут ознакомиться.

V. ЭМПИРИЧЕСКОЕ ПРОСТРАНСТВО. СИНКРЕТИЧЕСКАЯ ГЕОМЕТРИЯ.

Когда Декарт воображал три взаимоперпендикулярные прямые, пересекающиеся в одной точке, он мыслил перед собой всю объемлющую нас пустоту, в которой двигаются мириады разнообразных и разноразмерных материальных тел. Они прочерчивают в трехмерном пространстве свои траектории, меняя в каждый момент времени свои координаты, создавая абстракцию линии (по определению Камилла Жордана). Это представление о соотношении геометрической (мыслимой) теории и реального (эмпирического) пространства было долгое время бесспорным.

Мысль Альберта Эйнштейна о том, что можно понять мир чисто умозрительным путем не кажется мне чересчур смелой.

Источник

1 Кардинальные числа

3 Супернатуральные числа

где z – произвольное гиперкомплексное число.

.

Алгебру с расширенными таким образом числами называют алгеброй гипердействительных чисел. Таким образом,

Гипердействительные числа – это числа вида

2) ∞ = 1 / e – бесконечно большое число.

Гипердействительные числа не являются числами в обычном понимании. Несмотря на то, что они состоят из двух частей, они не двумерны. Вторая часть гиперкомплексного числа – это действительная вариация вещественного числа. Вариация – это бесконечно маленькое число со знаком. Бесконечно маленькое положительное число меньше любого положительного числа, не равного нулю, но больше нуля. Но такого числа не существует, потому что самое маленькое положительное число, меньшее другого положительного, есть нуль. Получили противоречие. Несмотря на это противоречие, гипердействительные числа имеют свое логически непротиворечивое применение в дифференциальном исчислении.

Бесконечно малые числа определяются как предел последовательности чисел, сходящихся к нулю, а бесконечно большие числа – как предел бесконечно возрастающей последовательности, не имеющей предела. Несмотря на то, что бесконечно малые числа очень близки к нулю, они не равны друг другу. Их отношение может быть любым числом и даже бесконечным числом.

Гипердействительные числа можно определить как сходящиеся последовательности чисел или как число, сложенное с бесконечно малым числом.

Гипердействительные числа применяются во многих разделах математики, особенно в теории пределов, дифференциальном и интегральном исчислениях, а также везде, где используются предельные последовательности, даже при определении самих вещественных чисел.

5 p-адические число

p-ади́ческое число (произносится: пэ-адическое) — элемент расширения поля рациональных чисел, являющегося пополнением поля рациональных чисел относительно p-адической нормы, которая определяется на основе свойств делимости целых чисел на заданное простое число р.

p-адические числа были введены Гензелем (нем.) в 1897 году[1].

Поле p-адических чисел обычно обозначается или .

Целым p-адическим числом для произвольного простого p называется бесконечная последовательность вычетов x_n по модулю p_n, удовлетворяющих условию

Сложение и умножение целых p-адических чисел определяется как почленное сложение и умножение таких последовательностей. Для них непосредственно проверяются все аксиомы кольца.

Определение через проективный предел

В терминах проективных пределов кольцо целых p-адических чисел определяется как предел

колец вычетов по модулю pn относительно естественных проекций .

Эти рассмотрения можно провести в случае не только простого числа p, но и любого составного числа m — получится т. н. кольцо m-адических чисел, но это кольцо в отличие от обладает делителями нуля, поэтому дальнейшие построения, рассматриваемые ниже, к нему неприменимы.

Обычные целые числа вкладываются в кольцо p-адических чисел очевидным образом: x = <x,x. > и являются подкольцом.

Беря в качестве элемента класса вычетов число , такое, что , мы можем записать каждое целое p— адическое число в виде x = <a1,a2. > однозначным образом. Такой вид называется каноническим. Записывая каждое a_n в p-ичной системе счисления и учитывая что мы можем всякое p-адическое число в каноническом виде представить в виде или записывая в виде бесконечной последовательности цифр в p-ичной системе счисления . Действия над такими последовательностями производятся по обыкновенными правилами сложения, вычитания и умножения «столбиком» в p-ичной системе счисления (в нашем примере p=5).

В такой форме записи натуральным числам и нулю соответствуют p-адические числа с конечным числом ненулевых цифр, точно таких, как у исходного числа. Отрицательным числам соответствуют p-адические числа с бесконечным числом ненулевых цифр, например в пятеричной системе −1=…4444=(4).

Кольцо целых p-адических чисел обычно обозначается .

Определение как поля частных

p-адическим числом называется элемент поля частных кольца целых p-адических чисел. Это поле называется полем p-адических чисел.

Поле p-адических чисел содержит в себе поле рациональных чисел. Нетрудно доказать, что любое целое p-адическое число, не кратное p обратимо в кольце , а кратное p однозначно записывается в виде xpn, где x не кратно p и поэтому обратимо, а n > 0, то ясно, что любой ненулевой элемент поля может быть записан в виде xpn, где x не кратно p а n любое, если n отрицательно, то исходя из представления целых p-адических чисел в виде последовательности цифр в p-ичной системе счисления мы можем записать любое такое p-адическое число в виде последовательности , то есть формально в виде в виде p-ичной дроби с конечным числом цифр после запятой и, возможно, бесконечным числом ненулевых цифр до запятой. Деление таких чисел можно также производить аналогично «школьному» правилу, но начиная с младших, а не старших разрядов числа. Так, в той же пятеричной системе имеем:

Любое рациональное число r можно представить как где a и b целые числа, не делящиеся на p, а n — целое. Тогда | r | p — p-адическая норма r — определяется как p − n. Если r = 0, то | r | p = 0.

Поле p-адических чисел есть пополнение поля рациональных чисел с метрикой dp, определённой p-адической нормой: dp(x,y) = | x − y | p. Это построение аналогично построению поля вещественных чисел как пополнения поля рациональных чисел при помощи нормы, являющейся обычной абсолютной величиной.

Норма | r | p продолжается по непрерывности до нормы на .

Каждый элемент x-поля p-адических чисел может быть представлен в виде сходящегося ряда

где n0 — некоторое целое число, а ai — целые неотрицательные числа, не превосходящие p − 1, а именно взяв в качестве ai цифры из записи p-адического числа x в виде последовательности цифр в системе счисления с основанием p. Такая сумма всегда сходится в метрике dp к самому x.

Числа с условием образуют кольцо целых p-адических чисел, являющееся пополнением кольца целых чисел в норме | x | p.

Числа с условием | x | p = 1 образуют мультипликативную группу и называются p-адическими единицами.

Совокупность чисел с условием | x | p < 1 является главным идеалом в с образующим элементом p.

метрическое пространство гомеоморфно Канторову множеству, а пространство гомеоморфно Канторову множеству с вырезанной точкой.

Для различных p нормы | x | p независимы, а поля неизоморфны.

Для любых элементов , r2, r3, r5, r7, …, таких что и , можно найти последовательность рациональных чисел xn, таких что для любого p, и .

Если — многочлен с целыми коэффициентами, то разрешимость при всех k сравнения

эквивалентна разрешимости уравнения

в целых p-адических числах. Необходимым условием разрешимости этого уравнения в целых или рациональных числах является его разрешимость в кольцах или, соответственно, полях p-адических чисел при всех p, а также в поле вещественных чисел. Для некоторых классов многочленов (например, для квадратичных форм) это условие является также достаточным.

На практике для проверки разрешимости уравнения в целых p-адических числах достаточно проверить разрешимость указанного сравнения для определенного конечного числа значений k. Например, согласно лемме Гензеля (Hensel’s lemma), при n = 1 достаточным условием для разрешимости сравнения при всех натуральных k служит наличие простого решения у сравнения по модулю p (то есть простого корня у соответствующего уравнения в поле вычетов по модулю p). Иначе говоря, при n = 1 для проверки наличия корня у уравнения в целых p-адических числах, как правило, достаточно решить соответствующее сравнение при k = 1.

Боревич З. И., Шафаревич И. Р. Теория чисел, — М.: Наука, 1985.

Коблиц Н. р-адические числа, р-адический анализ и дзета-функции, — М.: Мир, 1982.

Серр Ж.-П. Курс арифметики, — М.: Мир, 1972.

Б. Беккер, С. Востоков, Ю. Ионин 2-адические числа // Квант. — 1979. — Т. 2. — С. 26—31.

Источник