что такое геометрия лобачевского

Геометрия Лобачевского

Пятой аксиомой Евклида была аксиома о параллельных прямых, так называемый постулат о параллельных линиях, который гласит: если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которых меньше развернутого угла, то такие прямые пересекаются при достаточном продолжении с одной стороны. То есть эта аксиома утверждает, что существует только одна прямая, проходящая через данную точку вне данной прямой и параллельной этой данной прямой.

Сложная формулировка пятого постулата Евклида о параллельных линиях породила множество гипотез и предположений о возможной зависимости его от других постулатов. Были предприняты многочисленные попытки вывести его из остальных аксиом геометрии, но, к сожалению, они оказались тщетны. Усилия доказать пятый постулат от противного также не увенчались успехом.

И все же, в начале XX века почти одновременно несколько выдающихся математиков того времени — Карл Гаусс из Германии, Я. Больяи из Венгрии и Николай Иванович Лобачевский из России пришли к мысли о существовании другой, неевклидовой геометрии, в которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную.

Поскольку Н. И. Лобачевский первым высказал эту идею в 1826 году, новая неевклидова геометрия была названа в его именем.

Геометрия Лобачевского имеет лишь одно отличие от евклидовой — аксиома параллельности заменяется на ее отрицание — аксиому параллельности Лобачевского.

Аксиома параллельности Лобачевского выглядит следующим образом:

Найдутся такая прямая a и такая не лежащая на ней точка A, что через A проходят по крайней мере две прямые, не пересекающие a.

Непротиворечивость аксиомы доказывается представлением модели, в которой реализуются данные аксиомы.

Основы аналитической геометрии, заложенные Лобачевским, практически наметили необходимую для доказательства модель. Лобачевский заметил, что орисфера в пространстве изометрична евклидовой плоскости. Полностью реализовать модель смогли работы Клейна, Пуанкаре и других ученых.

Геометрия Лобачевского нашла широчайшее применение в современной науке. Сам Николай Иванович Лобачевский использовал свою геометрию для вычисления определенных интегралов.

В теории функций комплексного переменного геометрия Лобачевского способствовала успешному построению теории автоморфных функций. В этой теории связь с геометрией Лобачевского была основой для исследований Пуанкаре. По словам Анри Пуанкаре, «неевклидова геометрия есть ключ к решению всей задачи».

Кроме того, геометрия Лобачевского стала использоваться в теории чисел, а именно, в ее геометрических методах, так называемой «геометрии чисел».

Ученые также установили тесную связь геометрии Лобачевского с кинематикой — специальной теорией относительности. В основе этой связи лежит равенство, выражающее закон распространения света:

В общей теории относительности геометрия Лобачевского также нашла свое место. Допуская возможным тот факт, что распределение масс материи во Вселенной равномерно (это приближение в космических масштабах допустимо), то при определенных условиях пространство имеет геометрию Лобачевского. Тем самым было доказано предположение Лобачевского о новой геометрии как возможной теории пространства.

Источник

Геометрия Лобачевского

Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского.

Евклидова аксиома о параллельных (точнее, одно из эквивалентных ей утверждений) гласит:

Через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её.

В геометрии Лобачевского, вместо неё принимается следующая аксиома:

Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.

Содержание

История

Попытки доказательства пятого постулата

Отправным пунктом геометрии Лобачевского послужил V постулат Евклида — аксиома, эквивалентная аксиоме о параллельных. Он входил в список постулатов в «Началах» Евклида. Относительная сложность и неинтуитивность его формулировки вызывала ощущение его вторичности и порождала попытки вывести его как теорему из остальных постулатов Евклида.

Среди многих пытавшихся доказать пятый постулат были, в частности, следующие крупные учёные.

При этих попытках доказательства пятого постулата математики вводили (явно или неявно) некоторое новое утверждение, казавшееся им более очевидным.

Были предприняты попытки использовать доказательство от противного:

Наконец, стало возникать понимание о том, что возможно построение теории, основанной на противоположном постулате:

Создание неевклидовой геометрии

Лобачевский в работе «О началах геометрии» (1829), первой его печатной работе по неевклидовой геометрии, ясно заявил, что V постулат не может быть доказан на основе других посылок евклидовой геометрии, и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную, как и евклидова, и свободную от противоречий.

Одновременно и независимо к аналогичным выводам пришёл Янош Бойяи, а Карл Фридрих Гаусс пришёл к таким выводам ещё раньше. Однако труды Бойяи не привлекли внимания, и он вскоре оставил эту тему, а Гаусс вообще воздерживался от публикаций, и о его взглядах можно судить лишь по нескольким письмам и дневниковым записям. Например, в письме 1846 года астроному Г. Х. Шумахеру Гаусс так отозвался о работе Лобачевского:

Это сочинение содержит в себе основания той геометрии, которая должна была бы иметь место и притом составляла бы строго последовательное целое, если бы евклидова геометрия не была бы истинной… Лобачевский называет ее «воображаемой геометрией»; Вы знаете, что уже 54 года (с 1792 г.) я разделяю те же взгляды с некоторым развитием их, о котором не хочу здесь упоминать; таким образом, я не нашёл для себя в сочинении Лобачевского ничего фактически нового. Но в развитии предмета автор следовал не по тому пути, по которому шёл я сам; оно выполнено Лобачевским мастерски в истинно геометрическом духе. Я считаю себя обязанным обратить Ваше внимание на это сочинение, которое, наверное, доставит Вам совершенно исключительное наслаждение. [3]

В итоге Лобачевский выступил как первый наиболее яркий и последовательный пропагандист новой геометрии. Хотя геометрия Лобачевского развивалась как умозрительная теория, и сам Лобачевский называл её «воображаемой геометрией», тем не менее именно он впервые открыто предложил её не как игру ума, а как возможную и полезную теорию пространственных отношений. Однако доказательство её непротиворечивости было дано позже, когда были указаны её интерпретации (модели).

Утверждение геометрии Лобачевского

Лобачевский умер в 1856 году. Спустя несколько лет была опубликована переписка Гаусса, в том числе несколько восторженных отзывов о геометрии Лобачевского, и это привлекло внимание к трудам Лобачевского. Появляются переводы их на французский и итальянский языки, комментарии видных геометров. Публикуется и труд Бойяи.

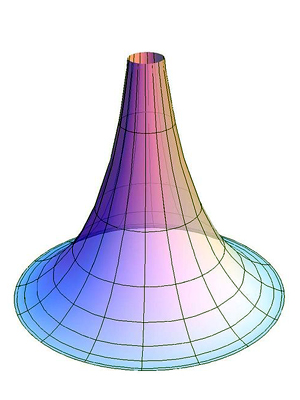
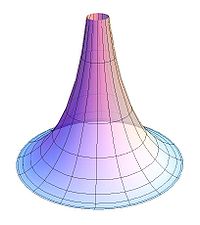
В 1868 году выходит статья Э. Бельтрами об интерпретациях геометрии Лобачевского. Бельтрами определил метрику плоскости Лобачевского и доказал, что она имеет всюду постоянную отрицательную кривизну. Такая поверхность тогда уже была известна — это псевдосфера Миндинга. Бельтрами сделал вывод, что локально плоскость Лобачевского изометрична участку псевдосферы (см. ниже). Окончательно непротиворечивость геометрии Лобачевского была доказана в 1871 году, после появления модели Клейна.

Вейерштрасс посвящает геометрии Лобачевского специальный семинар в Берлинском университете (1870). Казанское физико-математическое общество организует издание полного собрания сочинений Лобачевского, а в 1893 году столетие русского математика отмечается в международном масштабе.

Модели

Модели геометрии Лобачевского дали доказательство её непротиворечивости, точнее показали, что геометрия Лобачевского столь же непротиворечива, как геометрия Евклида.

Сам Лобачевский дал основы своей аналитической геометрии, и тем самым он уже фактически наметил такую модель. Он также заметил что орисфера в пространстве Лобачевского изометрична евклидовой плоскости, тем самым фактически предложил обратную модель. Тем не менее, само понятие о модели прояснилось в работах Клейна и других.

Псевдосфера

Итальянский математик Э. Бельтрами в 1868 году заметил, что геометрия на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной отрицательной кривизны, простейший пример которых представляет псевдосфера. Если точкам и прямым на конечном куске плоскости Лобачевского сопоставлять точки и кратчайшие линии (геодезические) на псевдосфере и движению в плоскости Лобачевского сопоставлять перемещение фигуры по псевдосфере с изгибанием, то есть деформацией, сохраняющей длины, то всякой теореме геометрии Лобачевского будет отвечать факт, имеющий место на псевдосфере. При этом длины, углы, площади понимаются в смысле естественного измерения их на псевдосфере.

Однако здесь даётся только локальная интерпретация геометрии, то есть на ограниченном участке, а не на всей плоскости Лобачевского.

Модель Клейна

В 1871 году Клейн предложил первую полноценную модель плоскости Лобачевского.

Плоскостью служит внутренность круга, прямой — хорда круга без концов, а точкой — точка внутри круга. «Движением» назовём любое преобразование круга в самого себя, которое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. Тогда оказывается, что любой геометрический факт, описанный на таком языке, представляет теорему или аксиому геометрии Лобачевского. Иными словами, всякое утверждение геометрии Лобачевского на плоскости есть не что иное, как утверждение евклидовой геометрии, относящееся к фигурам внутри круга, лишь пересказанное в указанных терминах. Евклидова аксиома о параллельных здесь явно не выполняется, так как через точку , не лежащую на данной хорде а (то есть «прямой»), проходит сколько угодно не пересекающих её хорд («прямых») (например, , ).

В этой модели расстояние между точками и на хорде определяется через двойное отношение

Модель Пуанкаре

Позже Пуанкаре, в связи с задачами теории функций комплексного переменного дал другую модель. За плоскость Лобачевского принимается внутренность круга, прямыми считаются дуги окружностей, перпендикулярных окружности данного круга, и его диаметры, движениями — преобразования, получаемые комбинациями инверсий относительно окружностей, дуги которых служат прямыми.

Модель Пуанкаре замечательна тем, что в ней углы изображаются обычными углами.

Поверхность постоянной отрицательной кривизны

Другое аналитическое определение геометрии Лобачевского состоит в том, что геометрия Лобачевского определяется как геометрия риманова пространства постоянной отрицательной кривизны. Это определение было фактически дано ещё в 1854 году Риманом и включало модель геометрии Лобачевского как геометрии на поверхностях постоянной кривизны. Однако Риман не связал прямо своих построений с геометрией Лобачевского, а его доклад, в котором он о них сообщил, не был понят и был опубликован лишь после его смерти (в 1868 году).

Содержание геометрии Лобачевского

Лобачевский строил свою геометрию, отправляясь от основных геометрических понятий и своей аксиомы, и доказывал теоремы геометрическим методом, подобно тому, как это делается в геометрии Евклида. Основой служила теория параллельных линий, так как именно здесь начинается отличие геометрии Лобачевского от геометрии Евклида. Все теоремы, не зависящие от аксиомы о параллельных, являются общими для обеих геометрий; они образуют так называемую абсолютную геометрию, к которой относятся, например, теоремы о равенстве треугольников. Вслед за теорией параллельных строились другие разделы, включая тригонометрию и начала аналитической и дифференциальной геометрии.

Приведём (в современных обозначениях) несколько фактов геометрии Лобачевского, отличающих её от геометрии Евклида и установленных самим Лобачевским.

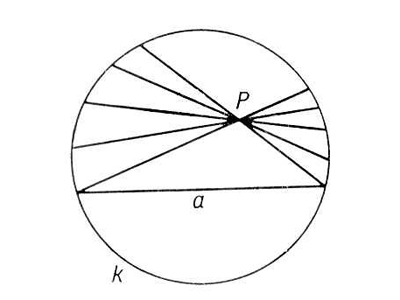
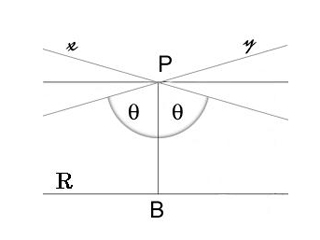
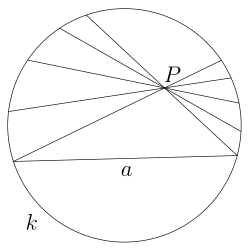
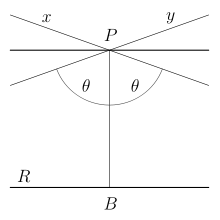
Через точку P, не лежащую на данной прямой R (см. рисунок), проходит бесконечно много прямых, не пересекающих R и находящихся с ней в одной плоскости; среди них есть две крайние x, y, которые и называются параллельными прямой R в смысле Лобачевского. В моделях Клейна (Пуанкаре) они изображаются хордами (дугами окружностей), имеющими с хордой (дугой) R общий конец (который по определению модели исключается, так что эти прямые не имеют общих точек).

Угол между перпендикуляром PB из P на R и каждой из параллельных (называемый углом параллельности) по мере удаления точки P от прямой убывает от 90° до 0° (в модели Пуанкаре углы в обычном смысле совпадают с углами в смысле Лобачевского, и потому на ней этот факт можно видеть непосредственно). Параллель x с одной стороны (а y с противоположной) асимптотически приближается к а, а с другой — бесконечно от неё удаляется (в моделях расстояния определяются сложно, и потому этот факт непосредственно не виден).

Для точки, находящейся от заданной прямой на расстоянии PB = a (см. рисунок), Лобачевский дал формулу для угла параллельности П(a) [4] :

Здесь q — некоторая постоянная, связанная с кривизной пространства Лобачевского. Она может служить абсолютной единицей длины аналогично тому, как в сферической геометрии особое положение занимает радиус сферы.

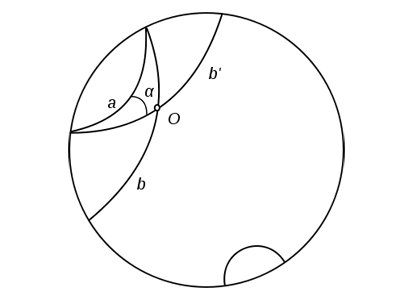
Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К любой из них можно восстановить перпендикуляры, которые не достигают другой прямой.

В геометрии Лобачевского не существует подобных, но неравных треугольников; треугольники равны, если их углы равны.

Сумма углов всякого треугольника меньше и может быть сколь угодно близкой к нулю. Это непосредственно видно на модели Пуанкаре. Разность , где , , — углы треугольника, пропорциональна его площади:

Из формулы видно, что существует максимальная площадь треугольника, и это конечное число: .

Линия равных расстояний от прямой не есть прямая, а особая кривая, называемая эквидистантой, или гиперциклом.

Предел окружностей бесконечно увеличивающегося радиуса не есть прямая, а особая кривая, называемая предельной окружностью, или орициклом.

Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность — предельная сфера, или орисфера; замечательно, что на ней имеет место евклидова геометрия. Это служило Лобачевскому основой для вывода формул тригонометрии.

Длина окружности не пропорциональна радиусу, а растёт быстрее. В частности, в геометрии Лобачевского число не может быть определено как отношение длины окружности к её диаметру.

Чем меньше область в пространстве или на плоскости Лобачевского, тем меньше геометрические соотношения в этой области отличаются от соотношений евклидовой геометрии. Можно сказать, что в бесконечно малой области имеет место евклидова геометрия. Например, чем меньше треугольник, тем меньше сумма его углов отличается от ; чем меньше окружность, тем меньше отношение её длины к радиусу отличается от , и т. п. Уменьшение области формально равносильно увеличению единицы длины, поэтому при безграничном увеличении единицы длины формулы геометрии Лобачевского переходят в формулы евклидовой геометрии. Евклидова геометрия есть в этом смысле «предельный» случай геометрии Лобачевского.

Заполнение плоскости и пространства правильными политопами

Плоскость Лобачевского может быть замощена не только правильными треугольниками, квадратами и шестиугольниками, но и любыми другими правильными многоугольниками. При этом в одной вершине паркета должно сходиться не менее 7 треугольников, 5 квадратов, 4 пяти- и шестиугольников и 3 многоугольников с числом сторон более 6. Каждое замощение (в одной вершине сходится M N-угольников) требует строго определённого размера единичного N-угольника, в частности, его площадь должна равняться:

В отличие от обычного пространства, которое можно заполнить правильными многогранниками только одним способом (по 8 кубов в вершине), трёхмерное пространство Лобачевского можно заполнить правильными многогранниками четырьмя способами:

Кроме этого, существует 11 способов заполнить пространство Лобачевского правильными мозаичными орисферами.

Источник

Геометрия Лобачевского

Из Википедии — свободной энциклопедии

Геометрия Лобачевского (или гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных аксиомах, что и обычная евклидова геометрия, за исключением аксиомы о параллельных прямых, которая заменяется её отрицанием.

Евклидова аксиома о параллельных (точнее, одно из эквивалентных ей утверждений, при наличии других аксиом) может быть сформулирована следующим образом:

На плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.

В геометрии Лобачевского вместо неё принимается следующая аксиома:

Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.

Аксиома Лобачевского является точным отрицанием аксиомы Евклида (при выполнении всех остальных аксиом), так как случай, когда через точку, не лежащую на данной прямой, не проходят ни одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её, исключается в силу остальных аксиом (аксиомы абсолютной геометрии). Так, например, сферическая геометрия и геометрия Римана, в которых любые две прямые пересекаются, и следовательно, не выполнена ни аксиома о параллельных Евклида, ни аксиома Лобачевского, не совместимы с абсолютной геометрией.

Геометрия Лобачевского имеет обширные применения как в математике, так и в физике. Историческое и философское её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии, математики и науки в целом.

Источник

Новое в блогах

О «Началах геометрии» Лобачевского

Вопрос о том, что отличает «Начала геометрии» Н.И. Лобачевского (17992-1856) от начал геометрии Евклида и что у них является общим, пока не имеет удовлетворительного ответа. Лобачевский в своей книге утверждает:

«Главное заключение, к которому пришёл я с предположением зависимости линий от углов, допускает существование геометрии более в обширном смысле, нежели как её представил нам первый Заклад. В этом пространственном виде дал я науке название Воображаемой Геометрии, где как частный случай входит употребительная геометрия с тем ограничением в общем положении которого требуют измерения в самом деле…».Цитата по: О началахъ Геометріи, соч. Г. Лобачевскаго

В «Математической энциклопедии» утверждается: «Лобачевского геометрия – геометрия, основанная на тех же основных посылках, что и евклидова геометрия, за исключением аксиомы о параллельных (см. Пятый постулат)».

Авторитетные математики утверждают: «Лобачевский пришёл к удивительному открытию: помимо геометрии Евклида существует другая геометрия, построенная на отрицании пятого постулата геометрии Евклида».

Утверждение «Математической энциклопедии» и авторитетных математиков даже не намекают на утверждение самого Лобачевского о том, что геометрия Евклида с её пятым постулатом является частным случаем геометрии Лобачевского с её пятым постулатом. Наоборот, утверждается прямо противоположное отношение геометрий, что геометрия Лобачевского построена на неполной геометрии Евклида, без её пятого постулата. Из извращённого отношения геометрий следует, что геометрия Лобачевского по своей неполной основе, в сравнении с полной геометрией Евклида, является неполной, другой геометрией.

Постулат геометрии Евклида утверждает: Через точку В, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её. Через точку В проходит прямая. Отрицанием данного утверждения является утверждение: через точку В не проходит прямая. Этого постулат геометрии Лобачевского не утверждает, а поэтому постулата не отрицает.

Постулат геометрии Лобачевского утверждает: Через точку В, не лежащую на данной прямой, проходит по меньшей мере две прямых, лежащих с данной прямой в одной плоскости и не пересекающих её. Через точку В проходит одна прямая, две прямых и больше. Нет отрицания пятого постулата геометрии Евклида. Наоборот, имеется его подтверждение в качестве частного случая. После появления геометрии Лобачевского и её пятого постулата евклидова геометрия и её постулат становятся частным случаем. Геометрия Евклида становится другой в отношении к геометрии Лобачевского. Авторитетный математик, неавторитетный в логике, переворачивает отношение геометрий и ставит на голову.

Геометрия Лобачевского заключает в себе математический анализ и математический синтез геометрических тел и их признаков. В геометрии Евклида нет анализа и синтеза геометрических тел и их признаков. Уже поэтому геометрия Евклида является другой геометрией в сравнении с геометрией Лобачевского. А геометрия Лобачевского не может называться другой геометрией, поскольку она заключает в себе геометрию Евклида. Логика – вещь упрямая, неподвластная никому.

Поэтому геометрия Лобачевского не может быть основанной на тех же основных посылках, что и евклидова геометрия. У геометрий различные основные посылки и различные методы изучения одних и тех же геометрических тел. В геометрии Лобачевского основные посылки анализируются и становятся другими – особенными и единичными. В геометрии Евклида основные посылки остаются одними и теми же.

Рассмотрим методы изучения шести форм понятия четырёхугольника в геометрии Евклида и в геометрии Лобачевского для их сравнения.

В геометрии Евклида трапеция, прямоугольник, параллелограмм, квадрат, произвольный четырёхугольник и ромб изучаются сами по себе, в отдельности, в состоянии покоя, существующими в определённом пространстве в течение неопределённого времени. Во время их изучения их форма, признаки, число признаков не изменяются. Признаки одной формы не становятся признаками другой формы. Порядок их изучения не имеет особого значения. Какие признаки и какое их число заключает в себе, например, форма трапеции или форма квадрата, имеют второстепенное значение. Не изучается ещё и другое их содержание. Всё, что в четырёхугольниках изучает геометрия Евклида, изучает и геометрия Лобачевского. Однако геометрия Лобачевского в четырёхугольниках изучает ещё их содержание, которое не изучает геометрия Евклида. Поэтому геометрия Лобачевского не является другой геометрией. В шести формах четырёхугольников выделяется самая совершенная форма, форма правильного четырёхугольника, иначе называемая квадратом. Квадрат имеет мысленную форму, заключающую в себе множество признаков. Она соответствует логической категории всеобщности, которую для краткости обозначим символом (В₁)

В множестве признаков квадрата выделяется подмножество собственных 7 признаков, которые образовались одновременно вместе с квадратом. Остальные признаки квадрата входят в другое подмножество признаков.

Собственные признаки квадрата удаляются из его формы и из внутреннего пространства в окружающее бесконечное пространство для хранения до востребования. Второе подмножество признаков, образовавшихся в другое время, остаётся на месте. Когда оно оказывается без первого подмножества, тогда оно сбрасывает с себя форму квадрата и принимает на себя форму параллелограмма. Параллелограмм и его признаки происходят из формы и признаков квадрата.

В множестве признаков параллелограмма выделяется подмножество собственных 7 признаков, которые образовались в одно время и вместе с параллелограммом. Остальные признаки параллелограмма вошли в другое подмножество признаков. Собственные признаки параллелограмма удаляются из его формы и из внутреннего пространства в окружающее бесконечное пространство для хранения до востребования. Второе подмножество признаков, образовавшихся в другое время, остаётся на месте. Когда оно оказывается без первого подмножества, тогда оно сбрасывает с себя форму параллелограмма и принимает на себя форму трапеции. Трапеция и её признаки произошли из формы и признаков параллелограмма. Чувственная форма параллелограмма соответствует логической категории всеобщности. Обозначим её символом (В).

В множестве признаков трапеции выделяется подмножество собственных 7 признаков, которые образовались в одно время и вместе с трапецией. Остальные признаки трапеции вошли в другое подмножество признаков.

Собственные признаки трапеции удаляются из её формы и из внутреннего пространства в окружающее бесконечное пространство для хранения до востребования. Второе подмножество признаков, образовавшихся в другое время, остаётся на месте. Когда оно оказалось без первого подмножества, тогда оно сбрасывает с себя форму трапеции и принимает на себя форму произвольного четырёхугольника. Он и его признаки произошли из формы и признаков трапеции. Чувственная форма трапеции соответствует логической категории особенности. Обозначим её символом (О).

В множестве признаков произвольного четырёхугольника выделяется подмножество собственных 7 признаков, которые образовались одновременно и вместе с произвольным четырёхугольником. Остальные его признаки вошли в другое подмножество признаков. Собственные признаки произвольного четырёхугольника удаляются из его формы и из внутреннего пространства в окружающее бесконечное пространство для хранения до востребования. Второе подмножество признаков, образовавшихся в другое время, остаётся на месте. Когда оно оказывается без первого подмножества, тогда оно сбрасывает с себя форму произвольного четырёхугольника и принимает на себя форму треугольника.

Треугольник и его признаки произошли из формы и признаков произвольного четырёхугольника. Можно анализировать треугольник до получения точки, но лучше это сделать позже, так как было принято решение сравнивать методы изучения шести форм понятия четырёхугольника. Чувственная форма произвольного четырёхугольника соответствует логической категории единичности. Обозначим её символом (Е). Для прямоугольника и ромба в процессе анализа не оказалось для них свободного места. Их происхождение остаётся пока неизвестным и выяснится позже.

Самым примечательным открытием в методе изучения четырёх форм понятия четырёхугольника является существование геометрических тел в состоянии движения, чего нет в евклидовой геометрии. Тела в состоянии движения обладают количеством движения. Эта характеристика метода фундаментально отличает его от метода изучения этих же тел в евклидовой геометрии.

Математический анализ избирает путь, прямо противоположный пути действительного развития тела. В этом заключается значение и предназначение математического анализа: предварительно пройти безумный путь в «никуда». После его завершения повторить его в обратном направлении посредством математического синтеза. В результате познаётся истина

Чтобы понять «Начала геометрии» Лобачевского, надо погрузить всё своё внимание вглубь содержания математического анализа сферы. Сфера посредством её анализа обращается в плоскость. Плоскость посредством её анализа обращается в прямую. Прямая посредством её анализа обращается в точку. Путь анализа – путь безумия. В природе совершенная форма тела не развивается в несовершенную форму.Но другого пути к познанию истины не существует. Он проходит через анализ. Только после прохождения пути анализа появляется возможность прохождения пути синтеза, повторяющего путь анализа к обратном направлении. Иначе невозможно познать действительное развитие точки в прямую, развитие прямой в плоскость, развитие плоскости в сферу. Причём, необходимо заострять внимание на переходе точки в прямую, и не задерживать внимание на прямой и на плоскости. Содержание перехода и обращения прямой в плоскость гораздо важнее содержания прямой и плоскости в отдельности.

Геометрия Евклида изучает прямую и плоскость в отдельности, полностью исключая обращение прямой в плоскость. Геометрия Лобачевского их изучает, но больше изучает процесс обращения прямой в плоскость посредством предварительного анализа и предварительного обращения плоскости в прямую. Двоичный путь в двух прямопротивоположных направлениях является методом изучения тел геометрии Лобачевского, непонятый математиками до настоящего времени.

«Геометрические свойства тел познаём в различном делении их на части. Они служат основанием геометрии и заключаются в следующем: всякое тело может быть разделено на части, которые не касаются через одну. Такие сечения назовём поступательными; число их неограниченно».Цитата по: О началахъ Геометріи, соч. Г. Лобачевскаго

Три поступательных сечения можно рассмотреть в более конкретной форме, на примере трёх поступательных сечений куба. Сечения задаются тремя протяжениями: высотой, шириной и длиной куба. Первое сечение лишает куб высоты. Второе сечение лишает куб ширины. Третье сечение лишает куб длины. Третье сечение завершает точка.

Например, высоту куба можно отсекать частями, горизонтальной плоскостью от верхнего основания до нижнего основания. Верхняя плоскость, которой принадлежит верхняя грань куба, будет опускаться вниз до предела. Внизу предельная плоскость всеми своими точками наложится на все точки неподвижной плоскости нижнего основания куба. Данное поступательное сечение завершается исчезновением высоты и порождением двоичной плоскости– подвижной и неподвижной. Верхняя сторона двоичной плоскости существует в состоянии движения в течение определённого времени в неопределённом бесконечном пространстве. Нижняя сторона двоичной плоскости существует в состоянии покоя в определённом ограниченном пространстве в течение неопределённого времени. На двоичной плоскости присутствуют четыре двоичные пересекающиеся прямые. На них присутствуют четыре двоичных стороны нижнего основания куба.

Поступательными сечениями вертикальной плоскости уменьшается двоичная ширина куба до предела. Остаётся троичная длина куба. Поступательными сечениями вертикальной плоскости уменьшается троичная длина куба до предела. Остаётся четверичная точка. Она является восьмой вершиной угла куба. Четверичная точка принадлежит четверичной прямой, которая принадлежит четверичной плоскости.

Поступательные сечения граней куба, в результате которых куб лишается высоты, ширины и длины, трёх протяжений, и появляются предельная плоскость, предельная прямая и предельная точка, являются моим примером. Примером Лобачевского являются поступательные сечения сферы, в результате которых сфера лишается высоты, ширины и длины, трёх протяжений, и появляются предельная плоскость, предельная прямая и предельная точка.

«Тело получает название поверхности, когда оно касается другого поверхностно и когда принимают в рассуждение только взаимное прикосновение сих двух тел; а потому дозволяют отбрасывать все части одного, неприкосновенные к другому. Так уничтожается одно из трёх протяжений, и так отделением ненужных частей поверхности доходим до тонкости листа бумаги, или как далеко может идти воображение». Цитата по: О началахъ Геометріи, соч. Г. Лобачевскаго

В бесконечном пространстве, которое не может изменять свою величину, высота сферы изменяется одновременно в пространственном виде в двух прямо противоположных направлениях. В одном направлении она увеличивается до бесконечности. В другом направлении она уменьшается до конечного предела и исчезает. Оба изменения величины высоты сферы вместе являются единством противоположностей.

«Всякое тело может быть разделено на части, которые все касаются взаимно, и которых число с каждым новым сечением увеличивается двумя. Такие сечения назовем обращательными; число их неограниченно».Цитата по: О началахъ Геометріи, соч. Г. Лобачевскаго

Уменьшается обращательным сечением одно протяжение сферы – появляется двоичная плоскость. Уменьшается обращательным сечением второе её протяжение – появляется четвричная прямая. Уменьшается обращательным сечением её третье протяжение – появлется восмиричная точка.

Можно в своём воображении представить себе на плоскости окружность и касательную прямую, имеющую с окружностью одну общую точку. Общая точка является основанием перпендикуляра, на котором присутствует центр окружности. Если центр окружности по перпендикуляру удаляется от общей точки до бесконечности, то и радиус окружности возрастает до бесконечности. В бесконечности все точки окружности оказываются наложенными на все точки прямой. Прямая становится двоичной, или предельной, прямой. Одна её сторона принадлежит ограниченному внутреннему пространству и её все точки находятся в состоянии покоя в течение неопределённого времени. Другая её сторона принадлежит неограниченному бесконечному окружающему пространству и её все точки находятся в состоянии движения в течение определённого времени. Двоичная предельная прямая линейно касается предельной окружности. Две стороны предельной прямой представляют собой единство противоположностей, двоичную прямую геометрии Лобачевского.

«Линией называется тело, которое касается линейно другого, и от которого дозволяют отбрасывать части, неприкосновенные к этому другому. Так доходим до тонкости волоса, до черты от пера на бумаге и пр. С обращением плоского тела в линию уничтожается второе протяжение, потому что линию образуют в пространстве два сечения, в которых поступательные сечения отделяют излишние части».Цитата по: О началахъ Геометріи, соч. Г. Лобачевскаго

Вторым главным сечением плоское тело, имеющее два протяжения, обращается в линейное тело с одним протяжением, в линию. Третьим главным сечением линейное тело, имеющее одно протяжение, обращается в точку, которая не имеет протяжений.

«Всякое тело может быть разделено тремя сечениями на 8 частей, которые все касаются взаимно. Такие сечения назовём тремя главными».Цитата по: О началахъ Геометріи, соч. Г. Лобачевскаго

«Тело получает название точки, когда рассматривают его прикосновение к другому в точке, а потому дозволяют отбрасывать части первого, неприкосновенные к другому. Так можно доходить до малости песчинки или точки от острия пера на бумаге».Цитата по: О началахъ Геометріи, соч. Г. Лобачевскаго

Обращение предельной сферы посредством математического анализа в двоичную предельную плоскость – безумие. Обращение двойной предельной плоскости посредством её анализа в троичную предельную прямую – безумие. Обращение тройной предельной прямой посредством анализа в четвертичную точку – безумие. Безумие человек в здравом уме понять не может. Не может совершенная форма тела обратиться сама по себе в своём естественном развитии в менее совершенную форму. Об этом написал при жизни Лобачевского Н.И. в критической статье «О началах геометрии, соч. г-на Лобачевского» аноним под псевдонимом из двух букв С. С. Цитата по: О началахъ Геометріи, соч. Г. Лобачевскаго

Анализ продолжает своё существование непосредственно в самом синтезе. Конец анализа – точка. Точка является началом синтеза. Качество синтеза зависит от качества анализа. В анализе произвольный четырёхугольник после удаления из него 7 собственных признаков обращается в треугольник. Правильный треугольник после удаления из него 7 собственных признаков обращается в произвольный треугольник. Произвольный треугольник после удаления из него 7 собственных признаков превращается в две пересекающиеся прямые. Две пересекающиеся прямые после удаления из них 7 собственных признаков обращаются в одну прямую, лежащую над плоскостью с одной своей точкой. Точка завершает анализ и является началом синтеза. В геометрии Лобачевского точка, прямая, плоскость являются двоичными, троичными, четверичными.

Математический анализ,описанный анонимом С.С., не является достаточно конкретным. Мне не удалось даже увидеть книгу «О началах геометрии», содержащую больше четырёхсот страниц. Вся моя информация о содержании книги сводится к цитированной С.С. её части. Мне пришлось анализ Лобачевского дополнять, не изменяя сущности содержания книги Лобачевского.

Я благодарен анониму С.С. за цитирование Лобачевского и выражаю один упрёк в его адрес. Мне оба определённых интеграла Лобачевского неизвестны, но два значения второго интеграла верны и находятся на своём месте. Известные два значения второго интеграла раскрывают его содержание. В анализе тремя главными поступательными сечениями тело делится на 8 частей. Если первое значение второго интеграла умножить на 8 и на радиус R = 1, то получается формула длины окружности геометрии Евклида С =2π R. При значении радиуса окружности R = ∞ длина окружности С = ∞. Два значения длины окружности находятся в необходимой связи, присущей единству противоположностей, конечной длине окружности ограниченного пространства и бесконечной длине окружности бесконечного пространства, все точки которой наложены на все точки первой прямой, пребывающей в состоянии покоя.

Более подходящей формой для описания синтеза является описание не в форме определённых интегралов, а посредством понятий геометрических тел и их признаков. В описании синтеза повторяется путь анализа в обратном направлении. Перевёрнутые и поставленные на голову отношения причины и следствия заново переворачиваются и ставятся на ноги.

Форма 1(Е).

А) Теория геометрии Евклида заключает в себе тела, существующие в состоянии покоя в определённом ограниченном пространстве в течение неопределённого времени. В этой форме присутствуют признаки:

— Одна точка.
— Одна прямая.
— Одна плоскость.
— Два луча в отдельности на прямой, имеющие общую точку и образующие развёрнутый угол (два единичных признака).
— Две полуплоскости в отдельности на плоскости, имеющие общую прямую и образующие развёрнутый угол (два единичных признака).

В форме всего 7 собственных признаков, существующих в отдельности.

Теория геометрии Лобачевского включает в себя 7 признаков геометрии Евклида, каждый из которых дополнен своей прямой противоположностью, своим антиподом. Антипод существует наложенным всеми точками на все точки своей противоположности. Он существует в состоянии движения в течение определённого времени в неограниченном бесконечном пространстве. Признаки по меньшей мере двоичны. Двоичная точка; двоичная прямая; двоичная плоскость; двоичные два луча на прямой, образующие развёрнутый угол; двоичные две полуплоскости на плоскости, образующие развёрнутый угол.

Двоичная точка в состоянии движения образует двоичную прямую, а двоичная прямая в состоянии движения образует двоичную плоскость В конце своего времени двоичная точка переходит из состояния движения в состояние покоя и становится неотличимой от точки геометрии Евклида. Все остальные признаки геометрии Лобачевского переходят из состояния движения в состояние покоя и становятся неотличимыми от признаков геометрии Евклида.

Поэтому можно в последующих формах рассматривать признаки геометрии Евклида, но иметь в виду их двоичность, троичность и четверичность.

Форма 2(О).

В этой форме сохраняются признаки единичной формы тел и образуются собственные 7 признаков, которые появляются вместе с появлением новой прямой, пересекающейся с данной прямой.

— Признаком 1 является вторая прямая, которая имеет одно протяжение.
— Признаком 2 является новая точка на новой прямой.
— Признаком 3 являются два луча, принадлежащие новой прямой.
— Признаками 4 и 5 являются два вертикальных угла первой пары. Вертикальные углы доказывают зависимость линий от углов.
— Признаками 6 и 7 являются два вертикальных угла второй пары. Пересекающиеся прямые зависят от вертикальных углов.

На каждую обычную точку наложена по меньшей мере одна предельная точка. На каждую обычную прямую наложена по меньшей мере одна предельная прямая. На обычную плоскость наложена по меньшей мере одна предельная плоскость. Два протяжения не являются принадлежащими всем собственным признакам, которым принадлежат собственные количества движения. Признаки обладают своим количеством движения и соответствуют особенности логической категории (О).

Форма 3(В).

В ней сохраняются все признаки предыдущей формы тел. Появляется новая прямая, пересекающая две данные прямые. Три пересекающиеся прямые образуют произвольный треугольник. Собственные признаки произвольного треугольника, связанные с новой прямой.

— Новая прямая, пересекающая данные пересекающиеся прямые.
— Появляется треугольник АВО.
— Угол А треугольника образует новая прямая с данными прямыми.
— Угол В треугольника образует новая прямая с данными прямыми.
— Сторону АВ образует новая прямая с данными прямыми.
— Треугольник АВО образует новая прямая с даннми прямыми.
— Сторона АВ принадлежит новой прямой.

Каждый собственный признак произвольного треугольника обладает в состоянии движения своим количеством движения, источником которого является бесконечное количество движения бесконечного пространства. Во всеобщей чувственной форме на каждую обычную точку наложена по меньшей мере одна предельная точка. На каждую обычную прямую наложена по меньшей мере одна предельная прямаяэ На обычную плоскость наложена по меньшей мере одна предельная плоскость. Её признаки обладают своим количеством движения, источником которых является бесконечное количество движения.

Всеобщая форма произвольного треугольника АВО соответствует логической категории всеобщности (В).

Форма 4(В₁).

Произвольный треугольник АВО в процессе движения, изменения и развития изменяет свою форму, которая становится всеобщей мысленной, предельно совершенной формой правильного треугольника АВО. Она заключает в себе вместе с другими признаками 7 собственных признаков.

Признаки правильного треугольника АВО:
— Правильный треугольник.
— Равные стороны.
— Равные углы треугольника.
— Равные высоты.
— Равные медианы.
— Три оси симметрии, образовавшиеся из биссектрис.
— Центр симметрии, образовавшийся из точки пересечения медиан.

Собственные 7 признаков являются двойными. На каждый обычный признак наложен предельный признак, все точки которого наложены на все точки обычного признака. Каждый собственный признак существует в состоянии движения и обладает своим количеством движения, источником которого является бесконечное количество движения, принадлежащее бесконечности, существующей в состоянии движения. Четыре формы понятия треугольника заключают в себе 28 признаков, которые становятся признаками правильного треугольника. Форма правильного треугольника исключает дальнейшее развитие. Она соответствует логической категории всеобщности (В₁). Любое изменение формы правильного треугольника является её обращением в менее совершенную форму с меньшим числом признаков. Уменьшение числа признаков уменьшают количество движения правильного треугольника, которое выходит из его формы в окружающее бесконечное пространство. Это значит, что предельное количество движения из бесконечного количества движения входит в правильный треугольник и из него возвращается к своему исходному пункту. На рис.4 присутствуют по меньшей мере два правильных треугольника: треугольник А и треугольник В. Треугольник А в состоянии движения обладает своим количеством движения А. Треугольник В обладает своим количеством движения В. Величина количества движения А должна отличаться от величины количества движения В в несколько раз по меньшей мере в два раза.

Форма 5(О₁).

На трёх прямых лежат три стороны треугольника, образующие его углы. Одна из трёх вершин угла треугольника, в которой пересекаются две прямые двух его сторон, удаляется в бесконечность. Эта особенная форма разлагающегося правильного треугольника наглядно подтверждает существование особенной зависимости трёх двойных прямых от трёх углов. Аналогичная зависимость линий от углов была открыта Лобачевским Н.И. во время исследований пятого постулата геометрии Евклида. Если вершину угла треугольника удалять от противоположной прямой, на которой лежит противоположная сторона, то угол будет уменьшаться, а два угла будут возрастать до своего предела. Когда вершина угла удалится и достигнет бесконечности, тогда длина его двух сторон достигнет бесконечности. В результате треугольник обратится в двухугольник, который удовлетворяет одновременно и вместе пятой аксиоме геометрии Евклида и пятой аксиоме геометрии Лобачевского.

Пятая аксиома геометрии Евклида утверждает:

Через точку В, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её.

Пятая аксиома геометрии Лобачевского утверждает:

Через точку В, не лежащую на данной прямой, проходит по меньшей мере две прямых, лежащих с данной прямой в одной двойной плоскости и не пересекающих её.

Тело (рис. 5), образуют двоичные три прямые, пересекающиеся в двух точках: в точке В и в точке О. Через точку В проходит двоичная прямая геометрии Лобачевского. Одна из них принадлежит предельной плоскости, в которую обратилась посредством математического анализа предельная сфера. Другая прямая принадлежит обычной плоскости. Все точки одной прямой наложены на все точки другой прямой. Предельная прямая обладает своим количеством движения. Его источником является бесконечное количество движения, существующее в бесконечности. На ограниченной конечной области определения геометрии Евклида они не могут быть доказаны. Поэтому более 2000 лет попытки доказать пятый постулат геометрии Евклида не имели успеха и не могли его иметь на ограниченной области определения евклидовой геометрии.

Форма 6(Е₁).

Особенная форма признаков правильного треугольника продолжает разлагаться и распадаться. Число признаков продолжает уменьшаться. За исчезновением одного угла и его двух сторон исчезают и остальные углы и их стороны. В результате остаются три прямых, которые не имеют точек пересечения.

Прямая, принадлежащая форме 1(Е) понятия треугольника, находясь в состоянии движения и развития, принимает на себя вторую пересекающую прямую, находящуюся в состоянии движения. К 7 собственным признакам формы 1(Е) добавляются 7 собственных признаков второй прямой. Признаки в состоянии движения обладают своим нефиксируемым количеством движения. Источником нефиксируемого количества движения формы тела является бесконечное количество движения бесконечного пространства, которое является бесконечной областью определения геометрии Лобачевского, но не принадлежит ограниченной области определения геометрии Евклида.

Более совершенная форма 2(О) понятия треугольника, заключает в себе две пересекающиеся прямые. Она обладает более развитым содержанием, которому соответствует большее количество признаков и большее нефиксируемое количество движения.

Более совершенная форма 3(В) заключает в себе три пересекающиеся прямые. Они обладают более развитым содержанием, которому соответствует большее количество признаков признаков и большее нефиксируемое количество движения.

Более совершенная форма 4(В₁) заключает в себе три пересекающиеся прямые, которые заключают в себе правильный треугольник. Ему соответствует большее количество признаков и большее нефиксируемое количество движения. Источником новых собственных признаков и добавочного количества движения является в бесконечном пространстве бесконечной области определения геометрии Лобачевского бесконечное нефиксируемое количество движения.Оно входит частицей в форму понятия и присутствует в ней в течение определённого времени в неопределённом пространстве в состоянии движения. Форма понятия треугольника существует в необходимой связи с формами физических тел. Существованию геометрических и физических тел в бесконечном пространстве соответствует их существование в течение конечных периодов времени в состоянии движения и изменения. В четырех формах понятия треугольника своего присутствия нефиксируемое количество движения не может обнаруживать. Нефиксируемое количество движения впервые обнаруживает своё присутствие в фиксируемой форме в процессе разложения понятия треугольника. Только в процесс разложения правильного треугольника оно обнаруживается первый раз как фиксируемое количество движения в фиксируемой форме тепловой энергии.

Одновременно и вместе обнаруживается изумительно простое и наглядное доказательство пятого постулата геометрии Евклида и пятого постулата геометрии Лобачевского в разложении понятия правильного треугольника. Их доказательства не могли появиться в отдельности и в разное время ни в ограниченном пространстве области определения геометрии Евклида, ни в области определения математического анализа и математического синтеза геометрии Лобачевского.

Форма 1(Е).

Первая форма понятия четырёхугольника имеет пространственный вид произвольного четырёхугольника. Четырёхугольник образуется из треугольника, точки вне его и трёх прямых, проходящих через точку и через три вершины углов треугольника. Четырёхугольник является единичной формой единичных 7 собственных признаков, включая 28 признаков правильного треугольника. Первым собственным признаком является форма произвольного четырёхугольника. Вторым признаком является точка С вне треугольника.Признаками 3, 4 и 5 являются прямые СА, СО и СВ.

Признаком 6 является угол АСО. Признаком 7 является диагональ СО. Все собственные признаки являются единичными, существующими в состоянии движения в течение определённого времени в неопределённом бесконечном пространстве.Признаки в состоянии движения обладают своим количеством движения, источником которого является бесконечное количество движения бесконечного пространства.

Единичная форма единичных собственных признаков соответствует логической категории единичности (Е). Стороны четырёхугольника являются двоичными, признаками двоичных четырёхугольников.

Форма 2 (О).

В математическом анализе трапеция обращается в произвольный четырёхугольник Теперь, в математическом синтезе, произвольный четырёхугольник обращается в трапецию. Анализ был необходим для обнаружения собственных признаков трапеции. В синтезе они известны и необходимы для обращения произвольного четырёхугольника в трапецию. В анализе 7 собственных признаков трапеции удалялись из её формы и ограниченного пространства в окружающее бесконечное пространство до востребования. Теперь они востребованы синтезом и возвращаются из окружающего пространства в форму произвольного четырёхугольника для её обращения в форму трапеции. Можно поступить в мысленном эксперименте иначе. В произвольном четырёхугольнике две противоположные стороны заменить двумя параллельными сторонами. Во время их замены образуется трапеция и её собственные 7 признаков.

— Признаком 1 является форма трапеции.
— Признаком 2 являются её параллельные нижнее и верхнее основания.
— Признаком 3 являются равные накрест лежащие углы при диагонали.
— Признаком 4 является сумма углов, равная двум прямым углам, прилежащих к боковым сторонам.
— Признаком 5 могут быть равные боковые стороны;.
— Признаком 6 может быть ось симметрии в равнобочной трапеции.
— Признаком 7 может быть боковая сторона, равная по длине основанию.

Признаки в состоянии движения обладают своим количеством движения, источником которого является бесконечное количество движения бесконечного пространства.

Не все признаки являются общими. Особенные признаки принадлежат особенной форме трапеции, которая соответствует логической категории особенности (О).Трапеция существует в состоянии движения и изменения своей формы в течение определённого времени в неопределённом бесконечном пространстве. Стороны трапеции являются двоичными, наложенными одна на другую всеми своими точками.

В математическом анализе параллелограмм обращается в трапецию. Теперь, в математическом синтезе трапеция обращается в параллелограмм. Анализ был необходим для обнаружения собственных признаков параллелограмма. В синтезе собственные его признаки известны. Они необходимы для обращения трапеции в параллелограмм. В анализе 7 собственных признаков параллелограмма удалялись из его формы в окружающее пространство до востребования. Теперь они востребованы и возвращаются из окружающего пространства в форму трапеции и обращают её в параллелограмм. Можно поступить иначе. В трапеции две непараллельные стороны заменить двумя параллельными сторонами. Во время их замены образуется параллелограмм и его собственные признаки.

— Признаком 1 – форма параллелограмма.
— Признаком 2– параллельные боковые стороны.
— Признаком 3 – равные боковые стороны.
— Признаком 4 –равные нижнее и верхнее основания.
— Признаком 5 – точка пересечения диагоналей – центр симметрии.
— Признаком 6 – сумма углов, равная двум прямым при нижнем и верхнем основаниях.
-Признаком 7 – равные накрест лежащие углы при диагонали.

Всеобщая форма признаков, имеющая пространственный вид параллелограмма, соответствует логической категории всеобщности (В).

Параллелограмм существует в состоянии движения и изменения своей формы в течение определённого времени в неопределённом бесконечном пространстве. Признаки в состоянии движения обладают своим количеством движения, источником которого является бесконечное количество движения бесконечного пространства.Параллелограмм двоичен. На каждую обычную его сторону наложена по меньшей мере одна предельная сторона предельной прямой.

Форма 4(В₁).

Четвёртая форма понятия четырёхугольника является квадратом. В математическом анализе квадрат обращается в параллелограмм. Теперь параллелограмм обращается в правильный четырёхугольник. В синтезе собственные признаки квадрата известны и необходимы для обращения параллелограмма в квадрат. В анализе 7 собственных признаков квадрата были удалены из его формы в окружающее бесконечное пространство, для их сохранения до востребования Теперь они востребованы синтезом и возвращаются из окружающего пространства в форму параллелограмма и обращают её в форму квадрата. В форме квадрата собственные признаки могут появиться иначе. Для их появления необходимо в параллелограмме углы заменить прямыми углами и стороны заменить равными сторонами. Во время их замены параллелограмм обращается в квадрат с собственными признаками.

— Признаком 1 является форма квадрата.
— Признаком 2 являются равные четыре стороны.
— Признаком 3 являются равные четыре прямых угла.
— Признаком 4 являются равные две диагонали.
— Признаком 5 являются взаимно перпендикулярные диагонали.
— Признаком 6 являются две оси симметрии, которыми являются диагонали.
— Признаком 7 являются равные накрест лежащие углы при диагонали.

Всеобщая, предельно совершенная, мысленная форма квадрата чувственно не воспринимается. Она соответствует логической категории всеобщности (В₁). Квадрат существует в состоянии движения и изменения своей формы в течение определённого времени в неопределённом бесконечном пространстве. Признаки в состоянии движения обладают своим количеством движения, источником которого является бесконечное количество движения бесконечного пространства. Экспериментально доказать присутствие количества движения в любой из четырёх форм невозможно. Количество движения не имеет своей формы и не фиксируется. Оно в квадрате принимает форму признаков и от них не отличается. В форме квадрата на все точки со сторон наложены все точки сторон предельного квадрата. Дальнейшее развитие и совершенствование формы квадрата невозможно. Любое её изменение является переходом в менее совершенную форму с утратой части признаков.

Квадрат является концом процесса развития понятия четырёхугольника и началом процесса его разложения, распада и обращения в менее совершенную форму.

На рис. 4 по меньшей мере присутствуют четырёхугольник А и четырёхугольник В. Четырёхугольник А в состоянии движения обладает своим количеством движения А. Четырёхугольник В обладает своим количеством движения В. Величина количества движения А должна отличаться от величины количества движения В в несколько раз, по меньшей мере в два раза.

Форма 5(О).

Пятая форма понятия четырёхугольника является двоичной. Её представляют прямоугольник и ромб. Каждый из них не обладает тремя различными признаками квадрата. От одного квадрата они не могут произойти. И от двух квадратов они не могут произойти. Мне потребовалось полвека самодеятельных исследований, чтобы, наконец, прийти к этой пятой форме понятия. Например, трапеция образуется из произвольного четырёхугольника посредством приобретения 7 признаков. Параллелограмм образуется из трапеции посредством приобретения 7 признаков.Правильный четырёхугольник, иначе называемый квадратом, образуется из параллелограмма посредством приобретения 7 признаков. А прямоугольник и ромб обнаруживаются после квадрата, не приобретая новых признаков, а, наоборот, теряя три признака квадрата. Это явление является чудесным явлением, истоком и тайной происхождения всех мировых религий. Эта форма понятия четырёхугольника не появляется в математическом анализе. Она не появляется и в математическом синтезе. Она не может появиться в Науке с большой буквы. И поэтому наука не в состоянии обосновать её появление на этом свете.Это форма четырёхугольника появляется как манна небесная «из ничего» и «из ниоткуда».

Прямоугольник или ромб заключает в себе квадрат, но доказать экспериментально присутствие прямоугольника в квадрате, или присутствие ромба в квадрате, Наука любого времени не в состоянии ни посредством анализа, ни посредством синтеза, ни посредством анализа и синтеза вместе как единства противоположностей. В присутствие прямоугольника или ромба в квадрате можно только или верить, или не верить. Принцип веры в области определения науки не существует. Поверить в их присутствие в правильном четырёхугольнике – единственный выход из обнаружившегося положения. Это же относится к пятому постулату геометрии Евклида и к пятому постулату геометрии Лобачевского. В четырёх формах понятия треугольника и понятия четырехугольника количество движения возрастает за счёт бесконечного количества движения бесконечного пространства. В пятой форме впервые обнаруживается его присутствие и его возврат к своему исходному пункту. Раскрывается вечное существование кругооборота несотворимого и неуничтожимого необъятного количества движения и энергии. Теперь учёные собираются создавать прибор для обнаружения нефиксируемого количества движения и нефиксируемой энергии. Без прибора, который может создаваться веками и тысячелетиями гениями человеческого рода, можно рассматривать колебания маятника настенных часов типа ходиков. В начале периода времени гиря передаёт маятнику постоянную часть своей потенциальной энергии.Передача энергии маятнику визуально обнаруживается по повороту на небольшой угол храпового колена по часовой стрелке. В конце периода времени маятник передаёт гире вдвое меньшую порцию энергии. Передача энергии маятником гире визуально наблюдается по повороту храпового колеса на очень малый угол против часовой стрелки. В веществе маятника часов типа ходиков нет источника энергии, которую он в конце каждого периода времени передаёт гире. Невозможно изобрести прибор, который может фиксировать данное нефиксируемое количество движения, регулярно поступающее в вещество маятника часов. Гипотеза А. Эйнштейна о существовании скрытой переменной уже не гипотеза, а реальная объективность.

Прямоугольник и ромб продолжают процесс разложения и распадения формы и признаков квадрата. Определённое количество движения удаляется из прямоугольника и ромба в бесконечное окружающее пространство.

За четырьмя формами понятия треугольника следует появление четырёх форм понятия четырёхугольника и их признаков с принадлежащими им количествами движения. Они не имеют своей формы, не обнаруживают своего присутствия в признаках четырёх форм понятия четырёхугольника и появляются в первый раз в форме 5(О) в особенной форме «лишним» четырёхугольником, появившимся как бы «из ниоткуда».

Систему геометрических тел, соответствующую логической формуле, Лобачевский характеризовал таким образом:

«Когда два тела А и В касаются каждое третьего С в точке, тогда отдельное положение двух точек или так называемое расстояние их друг от друга, всякий раз будет определено, как скоро А и В соединены телом D, неприкосновенным к С, хотя бы при этом в А, В, D происходили перемены отделением, или присоединением новых частей, неприкосновенных к С, или те изменения в А и В, которые дозволяются в сём роде прикосновения А, В с С. Так циркуль служит для назначения расстояний. С такими понятиями о способе измерять протяжения, геометрия может быть ведена со всею строгостью доказательств в том порядке, в каком здесь ниже излагается». Цитата по: О началахъ Геометріи, соч. Г. Лобачевскаго

Что следует ниже в книге Лобачевского, мне, к сожалению, неизвестно.

Заключение.

А) Данная характеристика геометрии Лобачевского является неполной и недостаточной, так как мне не удалось достать и прочитать более чем четырёхсотстраничную книгу «О началах геометрии» Лобачевского Н. И. Например, не обнаружено отношение геометрии к закону всемирного тяготения Ньютона. По Лобачевскому, два тела соединяет в одно тело не взаимное тяготение двух тел, а прикосновение тел в точке в бесконечном пространстве.

В) Получен ответ на вопрос, что отличает геометрию Лобачевского от геометрии Евклида и что у них является общим. Геометрия Лобачевского имеет бесконечную область определения бесконечного пространства, а ограниченная область определения евклидовой геометрии является её частью.

С) За год до конца своей жизни Лобачевский назвал свою геометрию Пангеометрией, главенствующей и возвышающейся над всеми геометриями.

D) Пятый постулат геометрии Евклида не мог быть доказан на ограниченной области определения геометрии Евклида. Оба постулата не могут быть доказаны на ограниченной области определения математического анализа и синтеза геометрии Лобачевского. Они доказываются одновременно и вместе на неограниченной бесконечной области определения геометрии Лобачевского.

Источник