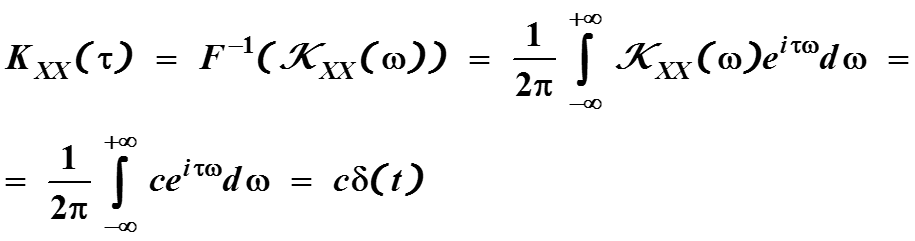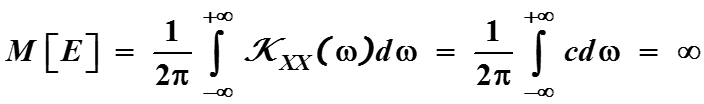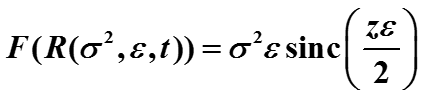что такое гауссовский белый шум
Аддитивный белый гауссов шум
Аддитивным белым гауссовским шумом называется вид мешающего воздействия, которое наблюдается в канале передачи данных.
Для такого шума характерны:

Функция Гаусса зависит от двух параметров:
1) математического ожидания (μ);
2) стандартного отклонения (σ).
В случае стандартного нормального распределения первый параметр равен нулю, второй – единице.
К аддитивному относится способ воздействия, при котором белый шум и полезный сигнал суммируются. Такой шум является наиболее распространенным для использования в расчетах и моделировании систем радиочастотной связи. Его противоположностью можно назвать такой шум, как мультипликативный, который с полезным сигналом не суммируется, а перемножается.
Гауссов шум и белый шум
Иногда гауссовский шум ошибочно считают обязательно белым. Но эти два понятия эквивалентными не являются.
Для гауссова шума характерно нормальное распределение значений сигнала, а вот термин «белый шум» относится к корреляции сигнала в два разных момента времени. При этом данная корреляция от распределения амплитуды шума не зависит.

Название «белый» шум получил от белого света, который содержит электромагнитные волны частот всего видимого диапазона электромагнитного излучения.
«Чисто» белый шум, то есть с одинаковой спектральной мощностью на всех частотах, в природе и технике не встречается. Иначе сигнал имел бы бесконечную мощность. Но под категорию белых попадают любые шумы с одинаковой (или слабо отличающейся) спектральной плотностью в рассматриваемом частотном диапазоне.
Применение
В физике и технике белый шум активно применятся. Например, в архитектурной акустике с целью сокрытия нежелательных шумов внутри зданий генерируют постоянный низкоамплитудный белый шум. Или еще он используется для измерения частотных характеристик разнообразных линейных динамических систем: усилителей, электронных фильтров, дискретных систем управления и т. д. Когда на вход такой системы подается белый шум, то на выходе получается сигнал, который является откликом системы на это приложенное воздействие.
Белый шум. Гауссовский белый шум. Физические источники белого шума
Страницы работы
Фрагмент текста работы
9.1. Определение белого шума
9.1. Определение белого шума
9.1. Определение белого шума
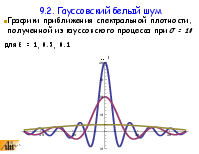
9.2. Гауссовский белый шум
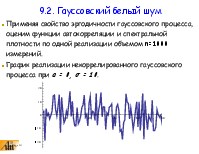
9.2. Гауссовский белый шум
В правой части получена функция, которая при ε 0 стремится к спектральной функции плотности KXX(ω) белого шума.
9.2. Гауссовский белый шум
9.2. Гауссовский белый шум
9.2. Гауссовский белый шум
9.2. Гауссовский белый шум
9.2. Гауссовский белый шум
9.2. Гауссовский белый шум
9.3. Физические источники белого шума
Соотношение сигнал к шуму — Белый Гауссовский Шум
Наряду с радиоволнами, несущими полезную информацию, на приемное устройство РТС воздействуют и помехи различной природы.
Какие шумы могут возникать в канале связи (КС)
Модель канала связи с шумами
Все шумы и помехи должны сложить с сигналом. Зачастую модель КС это именно аддитивная модель.
Аддитивная, значит шумы складываются с полезным сигналом. В качестве базовой модели КС используют канал с аддитивным белым гауссовским шумом (АБГШ).
Свойства АБГШ
Есть ось частот и спектр шума равномерен, на всех частотах одинаков и бесконечен, как в «+» так и в «-» по частоте, если мы говорим о комплексных сигналах. Либо он идет от 0, если мы говорим о реальных сигналах.
ВОПРОС. Почему в качестве базовой модели КС используется именно модель с АБГШ?
Это все вытекает из центральной предельной теоремы. Берем множество случайных сигналов, у этих сигналов есть плотности вероятности, абсолютно произвольные. Если мы сложим в эфире множество сигналов, то в итоге придем к тому, что сумма всех сигналов, будет Гауссовской.
Для примера, на картинке выше представлены прямоугольные плотности вероятности. Где n=1, это плотность вероятности для одного сигнала. Дальше взяли 2 сигнала с равномерной плотностью вероятности, сложили эти два сигнала и общая плотность вероятности уже будет треугольная. Взяли 3 сигнала, сложили, и плотность вероятности уже напоминает колокольчик. Для 5 сигналов, видим, что мы практически приблизились к Гауссовской функции. Если мы возьмем бесконечное количество таких сигналов, о получим гауссовское распределение. Нам не важно, какая плотность вероятности была, но когда мы сложим эти сигналы, в итоге придем к Гауссовскому сигналу.
Понятие отношение «сигнал/шум»
На вход приемника приходит смесь сигнала и шума. Чтобы качественно оценить на сколько много шума и сигнала пришло, пользуются отношением сигнал шум.
Есть отношение сигнал шум по мощности, когда средняя мощность сигнала делится на среднюю мощность шума, который попал в полосу приемника.
Когда говорят об отношении сигнал шум по мощности, то нужно подразумевать, о какой полосе идет речь. Если не говорят о конкретной полосе, т.е. сигнал шум в такой то полосе, то подразумевается, что полоса приемного фильтра совпадает с шириной спектра сигнала.
Виды шумов отношение сигнал/шум
Случайный процесс колеблется вокруг какого-то среднего значения, и значение это называется математическим ожиданием. Насколько сильно значение случайного процесса могут отличаться от мат. ожидания описывает параметр дисперсия — мера разброса случайной величины. Также в качестве меры разброса употребляется среднеквадратичное отклонение, также именуемое стандартным отклонением, значение его квадратный корень из дисперсии.
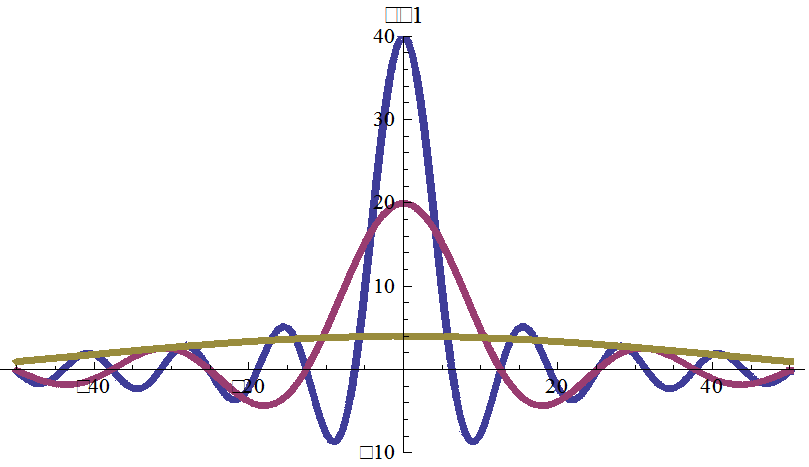
На рисунке представлены нормальные распределения четырех случайных процессов с разными значениями математического ожидания и дисперсии. В случае большего значения дисперсии, колокол Гауссовского распределения более широкий и низкий, что говорит о большей вероятности выпадения экстремальных значений и меньшей вероятности значений близких к мат. ожиданию.
В качестве меры скорости изменения случайного процесса может использоваться автокорреляционная функция, или просто корреляционная функция. Она описывает зависимость взаимосвязи сигнала с его сдвинутой во времени копией от величины временного сдвига.
В случае нулевого сдвига, сигналы полностью совпадают и значение автокорреляционной функции максимально. При увеличении расхождения это значение уменьшается. Причем для слабо изменяющихся во времени сигналов спад функции происходит медленнее чем для быстро изменяющихся.
Математическое ожидание, дисперсия, автокорреляционная функция это примеры численных характеристик, которыми можно описать случайный процесс. Законы изменения реальных физических величин весьма сложны, и для того чтобы мы могли описывать их доступным нам математическим аппаратом, нам часто приходится делать определенные допущения.
При описании сигналов случайными процессами, мы часто оговариваем свойства стационарности и эргодичности. Стационарным называется процесс в том случае, когда его плотность вероятности не зависит от временного сечения, то есть его статистические характеристики, мат ожидания, дисперсия, корреляционная функция не будут зависеть от времени. Стационарный процесс считается эргодическим, если для определения его характеристик вместо усреднения по ансамблю реализации, мы можем использовать усреднение по времени одной реализации, на практике нам обычно доступна только одна реализация случайного процесса.
Спектральная плотность мощности
Спектральная плотность мощности по определению это распределение мощности сигнала в зависимости от частоты, то есть мощность приходящаяся на единичный интервал частоты. Мы можем рассматривать спектральную плотность мощности как еще одну меру скорости изменения случайного процесса, она связана с корреляционной функции случайного процесса, теоремы Винера — Хинчина — Колмагорова.
Рассмотрим два синусоидальных сигнала разной частоты. Частотные области этих сигналов будут представлены двумя линиями. Положение линии на оси x говорит о величине частоты синусоиды, а длина линии, о ее мощности или амплитуде. Случайные процессы мы также можем рассматривать, как кусочки и отрезки различных синусоид, разной амплитуды и фазы, меняющейся быстро или медленно.
Спектр медленно изменяющегося случайного процесса содержит больше синусоид или спектральных компонент в левой части оси f, то есть в зоне низких частот. В то время как спектр быстро меняющегося процесса содержит больше компонент, большей амплитуды в правой части частотной оси.
Белый шум
Случайный процесс у которого область частот заполнено равномерно называется белым шумом.
Белый шум это стационарный случайный процесс, с равномерно распределенной спектральной плотностью мощности.
В таком процессе присутствуют компоненты изменяющиеся быстро, медленно, средне и ни одна из них не преобладает над другими.
Белый шум получил свое название по аналогии со спектром белого света. Известно, что белый цвет получается в результате сложения всех других цветов видимого диапазона.
Если в качестве аналогии и далее использовать видимый диапазон длин волн, то определенным цветом можно обозначить преобладание в спектре сигнала определенных компонент.
Если наложить красный светофильтр, то мы пропустим только более длинные волны, или более низкие частоты.
Если наложим синий фильтр, получим сигнал с относительно высокими частотами в спектре.
Цветовое обозначение частотного состава используется для описания так называемых цветных шумов, они никак не привязаны к какому-либо конкретному частотному диапазону и различаются только видом их спектральной плотности мощности. Цветные шумы, в том числе и белый шум это модели шумов, приближающие некоторые физические явления.
К примеру, процессы генерации и рекомбинации носителей заряда в цепях постоянного тока приводят к фликкер-шуму, который достаточно успешно описывается моделью розового шума. Красный шум описывает броуновское движение, модель серого шума используется в псих акустике и так далее.
Аддитивный белый гауссовский шум
Аддитивный белый гауссовский шум:
На системы беспроводной связи и обработки сигналов воздействует множество разнообразных широкополосных шумов, не связанных друг с другом. По центральной предельной теореме, распределение их суммарного воздействия будет близко к нормальному, именно поэтому данная модель наиболее распространена в системах ЦОС и системах связи, и используется как модель канала передачи данных.
Отношение сигнал/шум
Шум в подобных системах конечно же является нежелательным явлением. Одной из мер качества системы является отношение сигнал-шум. Это безразмерная величина равная отношению мощности полезного сигнала к мощности шума.
Отношение сигнал-шум часто измеряется в децибелах, для разных систем приемлемые значения этого отношения могут сильно отличаться, но в любом случае, чем выше этот показатель, тем лучше. Одна из задач цифровой обработки сигналов повышение отношения сигнал-шум, существуют разные способы повышения это фильтрация и усреднение.
Усреднение или когерентное накопление
Если мы сложим два одинаковых сигнала по фазе, то амплитуда результирующего сигнала будет вдвое больше. Положительные отсчёты сложатся с положительными, отрицательные с отрицательными.
Но сложить две реализации случайного процесса в фазе не получится, в каких-то точках произойдет усиление, каких-то ослабление шума. Проще говоря, при усреднении амплитуда шума не растет.
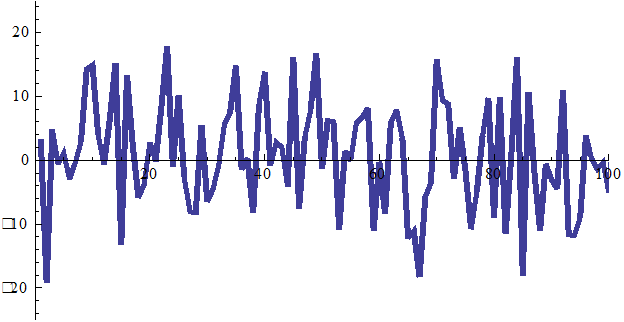
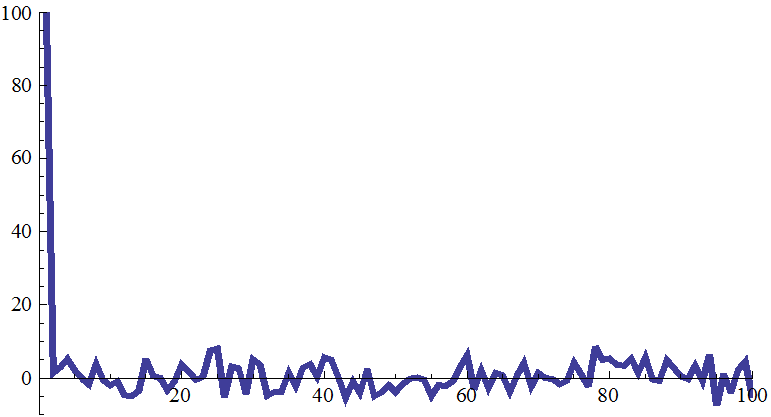
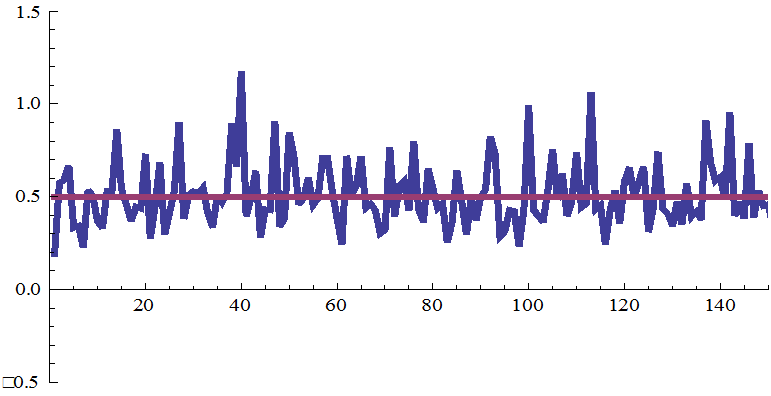
Накопление сигнала с шумом в matlab
Динамический диапазон и чувствительность
Динамический диапазон это характеристика системы, представляющая логарифм отношения максимального и минимального возможных значений величины входного параметра. Сверху этот диапазон обычно ограничен порогом искажений, а снизу так называемым шумовым дном, или чувствительностью.
Чувствительность это численный параметр равный уровню сигнала различимого системы над шумами, если у системы хорошая чувствительность, значит она меньше восприимчива к внешним помехам, имеет меньший уровень собственных шумов, и за счет этого способны различать сигналы малой энергетики.
Канал AWGN является хорошей моделью для многих каналов спутниковой связи и связи в дальнем космосе. Это не лучшая модель для большинства наземных линий связи из-за многолучевого распространения, блокировки местности, помех и т. Д. Однако для моделирования наземного пути AWGN обычно используется для моделирования фонового шума исследуемого канала в дополнение к многолучевости, блокировке местности и т. Д. помехи, помехи от земли и собственные помехи, с которыми современные радиосистемы сталкиваются при наземной эксплуатации.
Содержание
Емкость канала
C знак равно Максимум ж ( Икс ) ул E ( Икс 2 ) ≤ п я ( Икс ; Y ) <\ Displaystyle С = \ макс _ <е (х) <\ текст
E ( Y 2 ) знак равно E ( ( Икс + Z ) 2 ) знак равно E ( Икс 2 ) + 2 E ( Икс ) E ( Z ) + E ( Z 2 ) ≤ п + N <\ Displaystyle E (Y ^ <2>) = E ((X + Z) ^ <2>) = E (X ^ <2>) + 2E (X) E (Z) + E (Z ^ <2>) \ leq P + N \, \!>
Из этой оценки мы получаем из свойства дифференциальной энтропии, что
Таким образом, пропускная способность канала определяется максимально достижимой границей взаимной информации :
Пропускная способность канала и упаковка сфер
Достижимость
В этом разделе мы показываем достижимость верхней границы ставки из последнего раздела.
Принятые сообщения декодируются в сообщение в кодовой книге, которое является уникальным совместно типичным. Если такого сообщения нет или если ограничение мощности нарушено, объявляется ошибка декодирования.
Теорема кодирования обратная
Позвольте быть закодированным сообщением индекса кодового слова i. Потом: Икс я <\ displaystyle X_ >
Пусть будет средняя мощность кодового слова индекса i: п я <\ displaystyle P_ >
И при нормальном распределении у нас есть Y я <\ displaystyle Y_ >
час ( Y я ) ≤ 1 2 бревно 2 π е ( п я + N ) <\ displaystyle h (Y_ ) \ leq <\ frac <1><2>> \ log <2 \ pi e>(P_ + N) \, \!>
Поскольку каждое кодовое слово индивидуально удовлетворяет ограничению мощности, среднее значение также удовлетворяет ограничению мощности. Следовательно,
Мы можем применить это, чтобы упростить неравенство выше и получить:
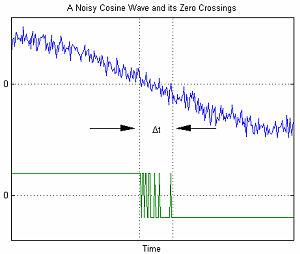
Эффекты во временной области
При последовательной передаче данных математическая модель AWGN используется для моделирования ошибки синхронизации, вызванной случайным джиттером (RJ).
При воздействии AWGN среднее количество переходов через ноль в положительном или отрицательном направлении в секунду на выходе узкополосного фильтра, когда на входе является синусоидальная волна, составляет
f 0 = центральная частота фильтра, B = ширина полосы фильтра, SNR = отношение мощности сигнал / шум в линейном выражении.
Эффекты в векторной области
График справа показывает пример того, как AWGN с ограниченной полосой частот может влиять на сигнал когерентной несущей. Мгновенный отклик вектора шума невозможно точно предсказать, однако его усредненный по времени отклик можно предсказать статистически. Как показано на графике, мы уверенно прогнозируем, что вектор шума будет находиться примерно 38% времени внутри круга 1σ, примерно 86% времени внутри круга 2σ и примерно 98% времени внутри круга 3σ.