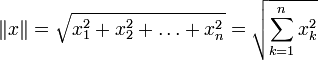что такое евклидово расстояние

Евклидова, L1 и Чебышёва — 3 основные метрики, которые пригодятся в Data Science

Авторизуйтесь

Евклидова, L1 и Чебышёва — 3 основные метрики, которые пригодятся в Data Science

Не важно, начинаете вы осваивать Data Science или работаете в этой сфере не первый год, вам наверняка пригодятся эти метрики. Разбираемся, что они из себя представляют и чем отличаются друг от друга.

Евклидово расстояние (расстояние по прямой)

Евклидово расстояние самое интуитивное для понимания: именно Евклидову метрику мы представляем, когда кто-то просит нас измерить расстояние между точками.

Евклидово расстояние — это прямая линия между двумя точками с координатами X и Y. Например, одной из таких точек может быть город на карте с его координатами долготы и широты.

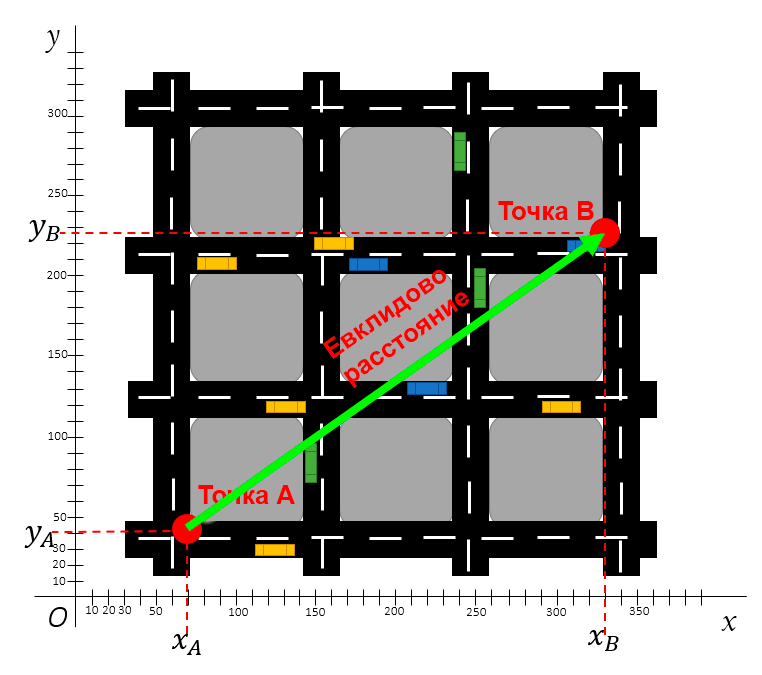
Евклидово расстояние характеризуется прямой линией. Допустим, вам нужно измерить расстояние по прямой между точками A и B на карте города, приведённой ниже.

Евклидово расстояние между двумя точками считается по теореме Пифагора

Для расчёта Евклидового расстояния вам понадобятся лишь координаты этих двух точек. Дистанцию между ними можно будет рассчитать по формуле Пифагора.

3–5 декабря, Онлайн, Беcплатно

Теорема Пифагора гласит, что можно рассчитать длину «диагональной стороны» (гипотенузы) прямого треугольника, зная длины его горизонтальной и вертикальной стороны (катетов). Формула выглядит так: a² + b² = c².

Пример расчёта Евклидового расстояния

Прим. ред. В четвёртой строке вычислений допущена ошибка: (-260)^2 = 67 600, а не 76 600. Тогда результат будет равен

Расстояние L1 (расстояние городских кварталов)

Расстояние L1 также известно как расстояние городских кварталов, манхэттенское расстояние, расстояние такси, метрика прямоугольного города — оно измеряет дистанцию не по кратчайшей прямой, а по блокам. Расстояние L1 измеряет дистанцию между городскими блоками: это расстояние всех прямых линий пути.

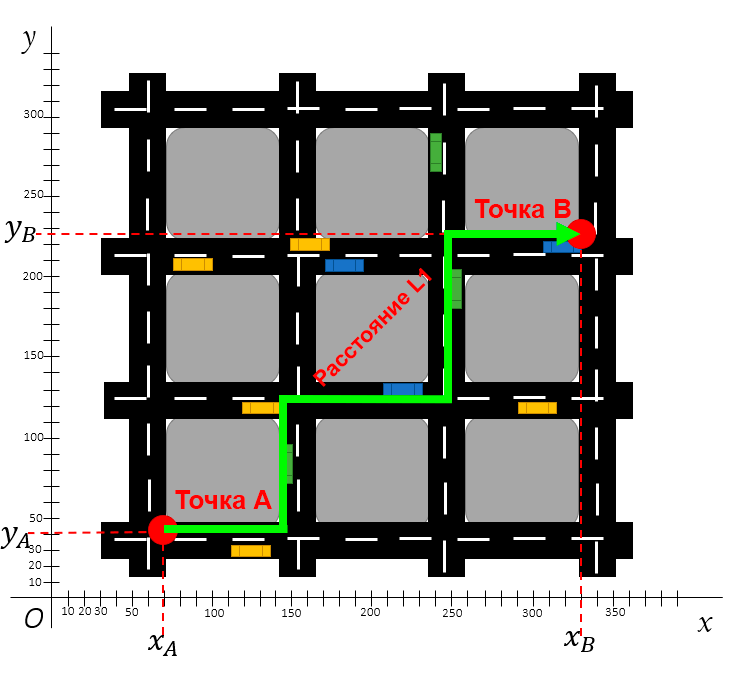
На следующем изображении показано расстояние L1 между двумя точками.

Расстояние L1 между двумя точками по блокам

Кроме показанного пути существует несколько альтернативных способов. Например, от точки A можно подняться на два блока вверх, а потом на три блока вправо, либо же на три блока вправо и два блока вверх.

Но расстояние L1 — это всё же просто дистанция, а поэтому траектория здесь не имеет значения. Единственное, что нужно понимать, это примерный путь: нужно пройти какое-то количество X блоков на восток и Y блоков на север. Сумма расстояний этих блоков и будет расстоянием L1 от точки A до точки B.

Пример расчёта расстояния L1 между двумя точками

Расстояние Чебышёва (метрика шахматной доски)

Расстояние Чебышёва известно ещё как расстояние шахматной доски. Чтобы понять принцип такой метрики, нужно представить короля на шахматной доске — он может ходить во всех направлениях: вперёд, назад, влево, вправо и по диагонали.

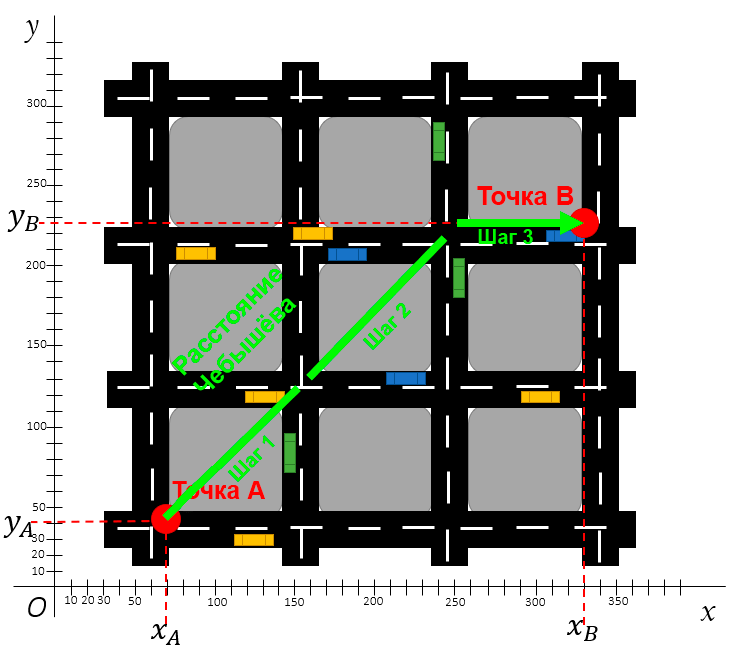
Расстояние Чебышёва между двумя точками

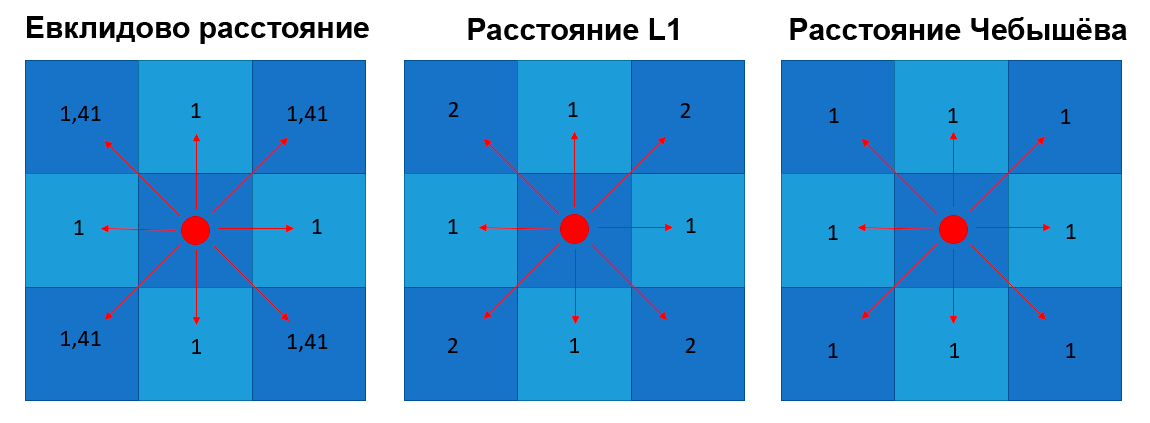
Разница расстояния L1 и расстояния Чебышёва в том, что при переходе на одну клетку по диагонали в первом случае засчитывается два хода (например вверх и влево), а во втором случае засчитывается всего один ход.

Ещё эти оба расстояния отличаются от Евклидового расстояния тем, что у Евклидового движение по диагонали рассчитывается по теореме Пифагора.

Сравнение путей 3 метрик

Расстояние Чебышёва можно представить как проход по шахматной доске.

Вот ещё один пример представления расстояния Чебышёва. Допустим, у вас есть дрон с двумя независимыми моторами: первый мотор тянет дрон вперёд, второй — в сторону. Оба мотора могут работать одновременно и равномерно на максимуме своей мощности.

Поэтому дрон может передвинуться на одну клетку по диагонали так же быстро, как по горизонтали или вертикали.

Посмотрите ещё раз на карту города по расстоянию Чебышёва. Первый шаг — оба мотора работают одновременно, второй шаг идентичен первому, а на третьем шаге мотор, тянущий дрон вперёд, отключается, и дрон смещается в сторону.

Таким образом, расстояние Чебышёва определяется как самая большая дистанция на одной оси.

Пример расчёта расстояния Чебышёва между двумя точками

Прим. ред. Полученный результат является условным и некорректно сравнивать его с другими результатами.

Источник

Расчет евклидова расстояния с помощью NumPy

В этом руководстве мы рассмотрим, как рассчитать евклидово расстояние между двумя точками в Python с помощью Numpy.

Что такое евклидово расстояние?

Евклидово расстояние — кратчайшая прямая между двумя точками в евклидовом пространстве.

Название происходит от Евклида, который широко известен как «отец геометрии», так как это было единственное пространство, которое люди в то время обычно задумывали. Со временем в физике и математике наблюдались различные типы пространства, такие как пространство Аффин.

В 3-мерном евклидовом пространстве кратчайшая прямая между двумя точками всегда будет прямой линией между ними.

Учитывая этот факт, евклидово расстояние не всегда является наиболее полезной метрикой для отслеживания при работе со многими размерностями, мы сосредоточимся на 2D и 3D евклидовом пространстве для расчета евклидова расстояния.

Вообще говоря, евклидова расстояние широко используется в разработке 3D-миров, а также алгоритмов машинного обучения, которые включают в себя метрики расстояния, такие как K-ближайшие соседи. Как правило, евклидово расстояние будет представлять, насколько похожи две точки данных, предполагая, что некоторая кластеризация на основе других данных уже была выполнена.

Математическая формула

Математическая формула расчета евклидова расстояния между 2 точками в 2D пространстве:

Формула легко адаптируется к 3D-пространство, а также к любому размеру:

Общая формула может быть упрощена до:

Острый глаз может заметить сходство между евклидовым расстоянием и теоремой Пифагора:

Из-за этого евклидова расстояние иногда называют расстоянием Пифагора, хотя прежнее название гораздо более известно.

Примечание: Две точки являются векторами, но выход должен быть скалярным.

Мы будем использовать NumPy для расчета этого расстояния для двух точек, и один и тот же подход используется для 2D и 3D пространств:

Расчет евклидова расстояния в Python с помощью NumPy

Во-первых, нам нужно будет установить библиотеку NumPy:

Теперь давайте импортируем его и настроим две наши точки с декартовыми координатами (0, 0, 0) и (3, 3, 3):

Вместо того, чтобы выполнять расчет вручную, мы будем использовать вспомогательные методы NumPy, чтобы сделать его еще проще!

Операции и математические функции, необходимые для расчета евклидова расстояния, довольно просты: сложение, вычитание, а также функция квадратного корня. Несколько слагаемых также можно заменить суммой:

NumPy предоставляет нам функцию np.sqrt(), представляющую функцию квадратного корня, а также функцию np.sum(), которая представляет собой сумму. При этом расчет евклидова расстояния в Python прост и интуитивно понятен:

Данная формула дает нам довольно простой результат:

Что равно 27. Осталось все, что получить квадратный корень из этого числа:

В истинном питоновом духе это можно сократить до одной строки:

Этот подход, однако, интуитивно больше похож на формулу, которую мы использовали раньше:

Это также приводит к:

np.linalg.norm()

Если бы вы установили для параметра ord какое-то другое значение p, вы бы рассчитали другие p-нормы. Например, норма L1 вектора-это расстояние Манхэттена!

Имея это в виду, мы можем использовать функцию np.linalg.norm() для легкого и гораздо более чистого вычисления евклидова расстояния, чем использование других функций:

Это приводит к печати расстояния L2/евклида:

Нормализация L2 и нормализация L1 широко используются в машинном обучении для нормализации входных данных.

Для расчета точечного произведения между 2 векторами вы можете использовать следующую формулу:

С помощью NumPy мы можем использовать функцию np.dot(), передавая два вектора.

Конечно, вы также можете сократить это до однострочного:

Использование встроенной системы math.dist()

В Python есть встроенный метод в математическом модуле, который вычисляет расстояние между 2 точками в трехмерном пространстве. Однако это работает только с Python 3.8 или более поздней версии.

math.dist()принимает два параметра, которые являются двумя точками, и возвращает евклидово расстояние между этими точками.

Примечание: Обратите внимание, что две точки должны иметь одинаковые размеры (т.е. оба в 2d или 3d пространстве).

Теперь, чтобы вычислить Евклидово расстояние между этими двумя точками, мы просто заправляем их в метод thedistdist():

Заключение

Данная метрика используется во многих контекстах в интеллектуальном анализе данных, машинном обучении и ряде других областей и является одной из фундаментальных метрик расстояния.

Источник

Евклидово расстояние: понятие, формула, расчет, пример

Содержание:

В Евклидово расстояние положительное число, которое указывает на разделение между двумя точками в пространстве, где выполняются аксиомы и теоремы геометрии Евклида.

Пространство, которое люди воспринимают и куда мы движемся, представляет собой трехмерное пространство (3-D), в котором выполняются аксиомы и теоремы геометрии Евклида. В этом пространстве содержатся двумерные подпространства (плоскости) и одномерные подпространства (линии).

Евклидовы пространства могут быть одномерными (1-D), двумерными (2-D), трехмерными (3-D) или n-мерными (n-D).

Формула

Евклидово расстояние d (A, B) между точками A и B, расположенными на прямой, определяется как квадратный корень из квадрата разностей их координат X:

Это определение гарантирует следующее: расстояние между двумя точками всегда положительное значение. И что расстояние между A и B равно расстоянию между B и A.

На рисунке 1 показано одномерное евклидово пространство, образованное линией (OX) и несколькими точками на этой линии. У каждой точки есть координата:

Евклидово расстояние в двух измерениях

— Одна линия проходит через две точки.

— Три точки на плоскости образуют треугольник, внутренние углы которого всегда составляют 180 °.

— В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.

В двух измерениях точка имеет координаты X и Y.

Например, точка P имеет координаты (XP, YP) ​​и координаты точки Q (XQ, YQ).

Евклидово расстояние между точками P и Q определяется по следующей формуле:

Следует отметить, что эта формула эквивалентна теореме Пифагора, как показано на рисунке 2.

Неевклидовы поверхности

Углы треугольника на сферической поверхности не составляют в сумме 180º, и при этом теорема Пифагора не выполняется, поэтому сферическая поверхность не удовлетворяет аксиомам Евклида.

Евклидово расстояние в n измерениях

Понятие координат можно расширить до более крупных размеров:

— В двухмерной точке P имеет координаты (XP, YP)

— В 3-D точка Q имеет координаты (XQ, YQ, ZQ)

— В 4-D точке R будет иметь координаты (XR, YR, ZR, WR)

Расстояние между двумя точками P и Q n-мерного евклидова пространства вычисляется по следующей формуле:

Геометрическое место всех точек Q в n-мерном евклидовом пространстве, равноудаленном от другой фиксированной точки P (центра), образуют n-мерную гиперсферу.

Как рассчитать евклидово расстояние

Ниже показано, как рассчитывается расстояние между двумя точками, расположенными в трехмерном евклидовом пространстве.

Мы хотим определить расстояние между этими точками, для чего используется общее соотношение:

d (A, B) = √ ((-3-2) 2 + (2-3) 2 + (2-1) 2) = √ ((-5) 2 + (-1) 2 + (1) 2 )

d (A, B) = √ (25 + 1 + 1) = √ (27) = √ (9 * 3) = 3 √ (3) = 5,196

пример

Требуется найти координаты средней точки M отрезка [PQ], соединяющего две точки.

Предполагается, что неизвестная точка M имеет координаты (X, Y, Z).

Поскольку M является серединой [PQ], должно быть верно, что d (P, M) = d (Q, M), поэтому d (P, M) ^ 2 = d (Q, M) ^ 2 также должно быть истинным:

Поскольку в этом случае третий член равен в обоих членах, предыдущее выражение упрощается до:

Тогда у нас есть уравнение с двумя неизвестными X и Y. Для решения проблемы требуется другое уравнение.

Точка M принадлежит прямой, проходящей через точки P и Q, которые мы можем вычислить следующим образом:

Вышеупомянутое уравнение известно как векторное уравнение прямой, которое в декартовых координатах принимает следующий вид:

Приравнивая соответствующие компоненты, получаем:

Он подставляется в квадратное выражение, связывающее X с Y:

Это упрощается, отменяя одинаковые условия в обоих членах:

Параметр a очищается:

То есть X = 4-5, Y = 6-1, наконец, Z = 1.

Наконец, мы получаем декартовы координаты средней точки M отрезка [PQ]:

Ссылки

Медитация как средство от фанатизма

Суицидология: что это такое, особенности и задачи этой науки

Источник

Евклидово расстояние

В математике термин евкли́дово простра́нство может обозначать один из сходных и тесно связанных объектов:

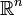
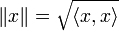
1. Конечномерное вещественное векторное пространство с введённым на нём (положительно определенным) скалярным произведением, порождающим норму:

,

в простейшем случае (евклидова норма):

где 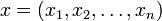(в евклидовом пространстве всегда можно выбрать базис, в котором верен именно этот простейший вариант).

Иначе говоря евклидово пространство — конечномерное гильбертово пространство.

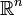
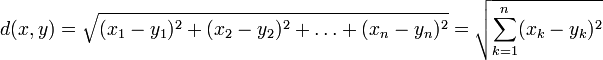
2. Метрическое пространство, которое является конечномерным векторным пространством над полем вещественных чисел с евклидовой метрикой, введённой по формуле:

,

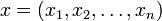
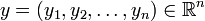
где и , то есть с функцией расстояния, порождаемой описанной выше нормой.

Содержание

Связанные определения

Примеры

Наглядными примерами евклидовых пространств могут служить пространства:

Можно привести и несколько более абстрактные примеры:

Не считается обычно евклидовым физическое 4-мерное пространство-время, т.к. основная метрика на нём, в соответствии с обычным в современной физике взглядом, псевдоевклидова. Хотя при желании евклидовская метрика может быть формально введена на нём тем или иным образом (если не пренебрегать гравитацией — то локально), что бывает иногда полезно, однако она не лоренц-инвариантна, что здесь очень сильно снижает её ценность с точки зрения современной физики.

См. также

Ссылки

Полезное

Смотреть что такое «Евклидово расстояние» в других словарях:

Евклидово пространство — (также Эвклидово пространство) в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3. В современном понимании, в более общем… … Википедия

Расстояние в математике — Метрическим пространством называется множество, в котором определено расстояние между любой парой элементов. Содержание 1 Формальное определение 2 Обозначения 3 Примеры … Википедия

Евклидово пространство — пространство, свойства которого описываются аксиомами евклидовой геометрии. Упрощенно можно определить евклидово пространство, как пространство на плоскости или в трехмерном объеме, в которых заданы прямоугольные (декартовы) координаты, а… … Начала современного естествознания

Евклидово пространство — (в математике) пространство, свойства которого описываются аксиомами евклидовой геометрии (См. Евклидова геометрия). В более общем смысле Е. п. называется n мepное Векторное пространство, в котором возможно ввести некоторые специальные… … Большая советская энциклопедия

Метод главных компонент — (англ. Principal component analysis, PCA) один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих областях,… … Википедия

Истинное ортогональное разложение — Метод Главных Компонент (англ. Principal components analysis, PCA) один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих… … Википедия

Метод Главных Компонент — (англ. Principal components analysis, PCA) один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих областях, таких как… … Википедия

Преобразование Карунена-Лоэва — Метод Главных Компонент (англ. Principal components analysis, PCA) один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих… … Википедия

Источник

Русские Блоги

1. Евклидово расстояние

Matlab рассчитывает расстояние, используя функцию pdist. Если X является матрицей m × n, то pdist (X) принимает каждую строку матрицы X как n-мерный вектор строк, а затем вычисляет расстояние между этими m векторами.

2. Манхэттен Расстояние

Matlab рассчитывает манхэттенское расстояние:

3. Чебышевское расстояние

В шахматах король может двигаться прямо, вбок и по диагонали, поэтому король может перейти на любой из восьми соседних квадратов за один шаг. Сколько шагов королю нужно пройти от сетки (x1, y1) до сетки (x2, y2)? Это расстояние называется расстоянием Чебышева.

Матлаб вычисляет чебышевское расстояние:

4. Минковский Расстояние

Когда p = 1, это манхэттенское расстояние;

Когда р = 2, это евклидово расстояние;

При p → ∞ это расстояние Чебышева.

Следовательно, согласно различным параметрам, расстояние Мин может представлять собой расстояние определенного типа / вида.

(2) Распределение (ожидание, дисперсия и т. Д.) Каждого компонента, не учитываемого, может отличаться.

Matlab вычисляет расстояние Мин (на примере Евклидова расстояния p = 2):

5. Стандартизированное евклидово расстояние

Определение: стандартизированное евклидово расстояние является улучшением по сравнению с недостатками евклидова расстояния. Идея стандартного евклидова расстояния: поскольку распределение компонентов в каждом измерении данных не одинаково, прежде всего «нормализуйте» каждый компонент к среднему значению и дисперсии. Предположим, что среднее значение выборочного набора X равно m, стандартное отклонение равно s, а «стандартизированная переменная» X выражается как:

Если обратная величина дисперсии рассматривается как вес, ее также можно назвать взвешенным евклидовым расстоянием.

Matlab вычисляет стандартизированное евклидово расстояние (при условии, что стандартные отклонения двух компонентов равны 0,5 и 1 соответственно):

6. Махаланобис Расстояние

Вывод расстояния Махаланобиса:

На приведенном выше рисунке есть две нормально распределенные группы населения, их средние значения a и b, но различия отличаются, поэтому какая группа населения ближе к точке A на рисунке? Или для кого A имеет большую вероятность? Очевидно, что A ближе к левому краю, и A, скорее всего, принадлежит левой популяции, хотя A имеет большее евклидово расстояние от a. Это интуитивное объяснение расстояния Махаланобиса.

Xm, ковариационная матрица обозначается как S, а среднее значение обозначается как вектор μ, тогда расстояние Махаланобиса от выборочного вектора X до μ выражается как:

Расстояние Махаланобиса между векторами Xi и Xj определяется как:

Если ковариационная матрица является единичной матрицей (выборочные векторы независимо и одинаково распределены), то расстояние Махаланобиса между Xi и Xj равно их евклидову расстоянию:

Если ковариационная матрица является диагональной матрицей, это стандартизированное евклидово расстояние.

Матлаб вычисляет расстояние Махаланобиса:

7. Косинус Расстояние

В геометрии угол косинуса может использоваться для измерения разницы между двумя направлениями вектора, а в машинном обучении эта концепция используется для измерения разницы между векторами выборки.

Matlab вычисляет косинус включенного угла (pdist (X, «косинус») в Matlab получает значение 1 минус включенный косинус угла):

8. Расстояние Хэмминга

Определение: Расстояние Хэмминга между двумя символьными строками одинаковой длины s1 и s2: минимальное количество замен символов, необходимое для замены одной на другую. Например:

Вес Хэмминга: это расстояние Хэмминга строки относительно нулевой строки той же длины, то есть это число ненулевых элементов в строке: для двоичной строки это число 1, поэтому Вес Хэмминга 11101 равен 4. Следовательно, если расстояние Хемминга между элементами a и b в векторном пространстве равно разности a-b их весов Хэмминга.

Применение: анализ веса Хэмминга имеет приложения в таких областях, как теория информации, теория кодирования и криптография. Например, в процессе кодирования информации, чтобы повысить отказоустойчивость, минимальное расстояние Хемминга между кодировками должно быть как можно большим. Однако, если вы хотите сравнить две строки разной длины, в этом случае обычно используются не только операции замены, но и операции вставки и удаления, в которых используются более сложные алгоритмы, такие как расстояние редактирования.

Matlab вычисляет расстояние Хемминга (расстояние Хемминга между двумя векторами в Matlab определяется как процентное соотношение различных компонентов двух векторов):

9. Джекард Расстояние

Коэффициент подобия Жакара (коэффициент сходства Жакара): доля пересечения двух множеств A и B в объединении A и B, называемая коэффициентом сходства Жакара двух множеств с символом J (A, Б) означает:

Matlab вычисляет расстояние Джакарты (Matlab определяет расстояние Джакарты как отношение числа различных измерений к «ненулевому измерению»):

10. Корреляционное расстояние

Matlab рассчитывает коэффициент корреляции и расстояние корреляции:

11. Информационная энтропия

Все вышеперечисленные методы измерения расстояния измеряют расстояние между двумя образцами (векторами), а информационная энтропия описывает расстояние между образцами во всей системе или концентрацию распределения образцов в системе (степень согласованности) ), Степень дисперсии, степень смешения (степень несоответствия). Чем более рассредоточено распределение выборки в системе (или чем оно более равномерно распределено), тем выше энтропия информации. Чем более упорядочено распределение (или чем более сконцентрировано распределение), тем меньше энтропия информации.

Происхождение информационной энтропии: пожалуйста, обратитесь к блогу: XXXXXXXX.

Формула для расчета информационной энтропии заданного выборочного набора X:

n: количество классификаций выборочного набора X

pi: вероятность появления i-го элемента в X

Чем больше информационная энтропия, тем более рассредоточено распределение выборочного набора S (распределенное равновесие) и чем меньше информационная энтропия, тем более концентрированное распределение выборочного набора X (несбалансированное распределение). Когда вероятность появления n категорий в S одинакова (все 1 / n), информационная энтропия принимает максимум log2 (n). Когда X имеет только одну категорию, информационная энтропия принимает минимальное значение 0.

Интеллектуальная рекомендация

Мяу Пасс Матрица SDUT

Мяу Пасс Матрица SDUT Time Limit: 1000 ms Memory Limit: 65536 KiB Submit Statistic Problem Description Лянцзян получил матрицу, но эта матрица была особенно уродливой, и Лянцзян испытал отвращение. Чт.

Гессенская легкая двоичная структура удаленного вызова

TCP Pasket и распаковка и Нетти Solutions

Основные введение TCP является ориентированным на соединение, обеспечивая высокую надежность услуг. На обоих концах (клиенты и терминалы сервера) должны иметь один или более гнезда, так что передающий.

Источник