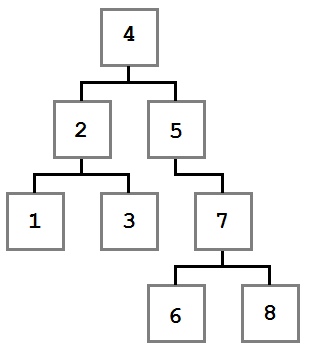
что такое двоичное дерево поиска
Дерево двоичного поиска
В этом руководстве вы узнаете, как работает двоичное дерево поиска. Здесь же собраны примеры реализации дерева двоичного поиска на Си, C++, Java и Python.
Дерево двоичного поиска — это структура данных, которая позволяет быстро работать с отсортированном списком чисел.
Чем отличается от обычного двоичного дерева
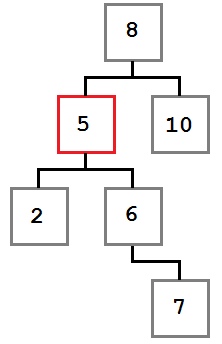
У правого дерева есть поддерево со значением 2, которое меньше, чем корень 3 — таким дерево двоичного поиска быть не может.
Операции с двоичным деревом поиска
Поиск элемента
Сложность в среднем: O(log n)
Сложность в худшем случае: O(n)
Алгоритм зависит от свойств дерева: у каждого левого поддерева есть значения, которые ниже корня или у каждого правого поддерева есть значения, которые выше корня.
Если значение ниже корня, мы можем точно сказать, что оно находится не в правильном поддереве. Тогда нам нужно искать только в левом поддереве. А если значение выше корня, можно точно сказать, что значения нет в левом поддереве. Тогда ищем только в правом поддереве.
Алгоритм:
Изобразим это на диаграмме.
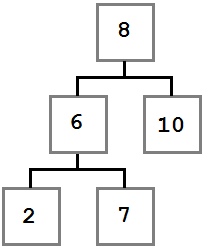
• Не нашли 4 → идем по левому поддереву корня 8
• Не нашли 4 → идем по левому поддереву корня 3
• Не нашли 4 → идем по левому поддереву корня 6
Если мы нашли значение, мы возвращаем его так, чтобы оно распространялось на каждом шаге рекурсии — рассмотрите рисунок ниже.
Если мы не нашли значение, значит, мы достигли левого или правого дочернего элемента листового узла, который имеет значение NULL — это значение также рекурсивно распространяется и возвращается.
Вставка элемента
Сложность в среднем: O(log n)
Сложность в худшем случае: ΘO(n)
Операция вставки значения похожа на поиск элемента. Мы также придерживаемся правила: левое поддерево меньше корня, правое поддерево — больше.
Мы продолжаем переходить либо к правому поддереву, либо к левому поддереву в зависимости от значения узла, и когда достигаем точки, в которой левое или правое поддерево имеет значение NULL, помещаем туда новый узел.
Алгоритм:
Алгоритм не такой простой, как может показаться на первый взгляд. Давайте визуализируем процесс.
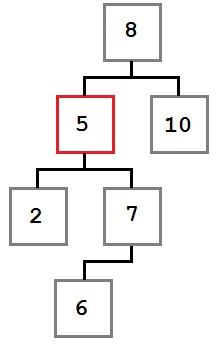
• 4 3 → идем через правого «ребенка» 3.
Таким образом, когда мы будем двигаться обратно вверх по дереву, связи других узлов не изменятся.
Корень возвращаем в конце — так ничего не сломается.
Удаление элемента
Сложность в среднем: O(log n)
Сложность в худшем случае: O(n)
Всего может быть три случая при удаление элемента из дерева двоичного поиска. Давайте рассмотрим каждый.
Случай I: лист
Первый случай — когда нужно удалить листовой элемент. Просто удаляем узел из дерева.
• Просто удалили узел.
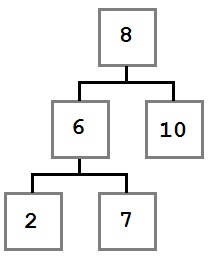
Случай II: есть дочерний элемент
Во втором случае у узла, который мы хотим удалить, есть один дочерний узел. В этом случае действуем так:
• Меняем 6 на 7 и удаляем узел 7.
•Нужный узел удален.
Случай III: два дочерних элемента
Если у узла, который мы хотим удалить, есть два потомка, делаем так:
Бинарные деревья поиска и рекурсия – это просто
Существует множество книг и статей по данной теме. В этой статье я попробую понятно рассказать самое основное.
Бинарное дерево — это иерархическая структура данных, в которой каждый узел имеет значение (оно же является в данном случае и ключом) и ссылки на левого и правого потомка. Узел, находящийся на самом верхнем уровне (не являющийся чьим либо потомком) называется корнем. Узлы, не имеющие потомков (оба потомка которых равны NULL) называются листьями.

Рис. 1 Бинарное дерево
Бинарное дерево поиска — это бинарное дерево, обладающее дополнительными свойствами: значение левого потомка меньше значения родителя, а значение правого потомка больше значения родителя для каждого узла дерева. То есть, данные в бинарном дереве поиска хранятся в отсортированном виде. При каждой операции вставки нового или удаления существующего узла отсортированный порядок дерева сохраняется. При поиске элемента сравнивается искомое значение с корнем. Если искомое больше корня, то поиск продолжается в правом потомке корня, если меньше, то в левом, если равно, то значение найдено и поиск прекращается.

Рис. 2 Бинарное дерево поиска
Сбалансированное бинарное дерево поиска — это бинарное дерево поиска с логарифмической высотой. Данное определение скорее идейное, чем строгое. Строгое определение оперирует разницей глубины самого глубокого и самого неглубокого листа (в AVL-деревьях) или отношением глубины самого глубокого и самого неглубокого листа (в красно-черных деревьях). В сбалансированном бинарном дереве поиска операции поиска, вставки и удаления выполняются за логарифмическое время (так как путь к любому листу от корня не более логарифма). В вырожденном случае несбалансированного бинарного дерева поиска, например, когда в пустое дерево вставлялась отсортированная последовательность, дерево превратится в линейный список, и операции поиска, вставки и удаления будут выполняться за линейное время. Поэтому балансировка дерева крайне важна. Технически балансировка осуществляется поворотами частей дерева при вставке нового элемента, если вставка данного элемента нарушила условие сбалансированности.

Рис. 3 Сбалансированное бинарное дерево поиска
Сбалансированное бинарное дерево поиска применяется, когда необходимо осуществлять быстрый поиск элементов, чередующийся со вставками новых элементов и удалениями существующих. В случае, если набор элементов, хранящийся в структуре данных фиксирован и нет новых вставок и удалений, то массив предпочтительнее. Потому что поиск можно осуществлять алгоритмом бинарного поиска за то же логарифмическое время, но отсутствуют дополнительные издержки по хранению и использованию указателей. Например, в С++ ассоциативные контейнеры set и map представляют собой сбалансированное бинарное дерево поиска.

Рис. 4 Экстремально несбалансированное бинарное дерево поиска
Теперь кратко обсудим рекурсию. Рекурсия в программировании – это вызов функцией самой себя с другими аргументами. В принципе, рекурсивная функция может вызывать сама себя и с теми же самыми аргументами, но в этом случае будет бесконечный цикл рекурсии, который закончится переполнением стека. Внутри любой рекурсивной функции должен быть базовый случай, при котором происходит выход из функции, а также вызов или вызовы самой себя с другими аргументами. Аргументы не просто должны быть другими, а должны приближать вызов функции к базовому случаю. Например, вызов внутри рекурсивной функции расчета факториала должен идти с меньшим по значению аргументом, а вызовы внутри рекурсивной функции обхода дерева должны идти с узлами, находящимися дальше от корня, ближе к листьям. Рекурсия может быть не только прямой (вызов непосредственно себя), но и косвенной. Например А вызывает Б, а Б вызывает А. С помощью рекурсии можно эмулировать итеративный цикл, а также работу структуры данных стек (LIFO).
Кратко обсудим деревья с точки зрения теории графов. Граф – это множество вершин и ребер. Ребро – это связь между двумя вершинами. Количество возможных ребер в графе квадратично зависит от количества вершин (для понимания можно представить турнирную таблицу сыгранных матчей). Дерево – это связный граф без циклов. Связность означает, что из любой вершины в любую другую существует путь по ребрам. Отсутствие циклов означает, что данный путь – единственный. Обход графа – это систематическое посещение всех его вершин по одному разу каждой. Существует два вида обхода графа: 1) поиск в глубину; 2) поиск в ширину.
Поиск в ширину (BFS) идет из начальной вершины, посещает сначала все вершины находящиеся на расстоянии одного ребра от начальной, потом посещает все вершины на расстоянии два ребра от начальной и так далее. Алгоритм поиска в ширину является по своей природе нерекурсивным (итеративным). Для его реализации применяется структура данных очередь (FIFO).
Поиск в глубину (DFS) идет из начальной вершины, посещая еще не посещенные вершины без оглядки на удаленность от начальной вершины. Алгоритм поиска в глубину по своей природе является рекурсивным. Для эмуляции рекурсии в итеративном варианте алгоритма применяется структура данных стек.
С формальной точки зрения можно сделать как рекурсивную, так и итеративную версию как поиска в ширину, так и поиска в глубину. Для обхода в ширину в обоих случаях необходима очередь. Рекурсия в рекурсивной реализации обхода в ширину всего лишь эмулирует цикл. Для обхода в глубину существует рекурсивная реализация без стека, рекурсивная реализация со стеком и итеративная реализация со стеком. Итеративная реализация обхода в глубину без стека невозможна.
Асимптотическая сложность обхода и в ширину и в глубину O(V + E), где V – количество вершин, E – количество ребер. То есть является линейной по количеству вершин и ребер. Записи O(V + E) с содержательной точки зрения эквивалентна запись O(max(V,E)), но последняя не принята. То есть, сложность будет определятся максимальным из двух значений. Несмотря на то, что количество ребер квадратично зависит от количества вершин, мы не можем записать сложность как O(E), так как если граф сильно разреженный, то это будет ошибкой.
DFS применяется в алгоритме нахождения компонентов сильной связности в ориентированном графе. BFS применяется для нахождения кратчайшего пути в графе, в алгоритмах рассылки сообщений по сети, в сборщиках мусора, в программе индексирования – пауке поискового движка. И DFS и BFS применяются в алгоритме поиска минимального покрывающего дерева, при проверке циклов в графе, для проверки двудольности.
Обходу в ширину в графе соответствует обход по уровням бинарного дерева. При данном обходе идет посещение узлов по принципу сверху вниз и слева направо. Обходу в глубину в графе соответствуют три вида обходов бинарного дерева: прямой (pre-order), симметричный (in-order) и обратный (post-order).
Прямой обход идет в следующем порядке: корень, левый потомок, правый потомок. Симметричный — левый потомок, корень, правый потомок. Обратный – левый потомок, правый потомок, корень. В коде рекурсивной функции соответствующего обхода сохраняется соответствующий порядок вызовов (порядок строк кода), где вместо корня идет вызов данной рекурсивной функции.
Если нам дано изображение дерева, и нужно найти его обходы, то может помочь следующая техника (см. рис. 5). Обводим дерево огибающей замкнутой кривой (начинаем идти слева вниз и замыкаем справа вверх). Прямому обходу будет соответствовать порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами слева. Для симметричного обхода порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами снизу. Для обратного обхода порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами справа. В коде рекурсивного вызова прямого обхода идет: вызов, левый, правый. Симметричного – левый, вызов, правый. Обратного – левый правый, вызов.

Рис. 5 Вспомогательный рисунок для обходов
Для бинарных деревьев поиска симметричный обход проходит все узлы в отсортированном порядке. Если мы хотим посетить узлы в обратно отсортированном порядке, то в коде рекурсивной функции симметричного обхода следует поменять местами правого и левого потомка.
Надеюсь Вы не уснули, и статья была полезна. Скоро надеюсь последует продолжение банкета статьи.
Алгоритмы и структуры данных для начинающих: двоичное дерево поиска
Авторизуйтесь
Алгоритмы и структуры данных для начинающих: двоичное дерево поиска
До сих пор мы рассматривали структуры данных, данные в которых располагаются линейно. В связном списке — от первого узла к единственному последнему. В динамическом массиве — в виде непрерывного блока.
В этой части мы рассмотрим совершенно новую структуру данных — дерево. А точнее, двоичное (бинарное) дерево поиска (binary search tree). Бинарное дерево поиска имеет структуру дерева, но элементы в нем расположены по определенным правилам.
25–27 ноября, Онлайн, Беcплатно
Для начала мы рассмотрим обычное дерево.
Деревья
Дерево — это структура, в которой у каждого узла может быть ноль или более подузлов — «детей». Например, дерево может выглядеть так:
Это дерево показывает структуру компании. Узлы представляют людей или подразделения, линии — связи и отношения. Дерево — это самый эффективный способ представления и хранения такой информации.
Дерево на картинке выше очень простое. Оно отражает только отношение родства категорий, но не накладывает никаких ограничений на свою структуру. У генерального директора может быть как один непосредственный подчиненный, так и несколько или ни одного. На рисунке отдел продаж находится левее отдела маркетинга, но порядок на самом деле не имеет значения. Единственное ограничение дерева — каждый узел может иметь не более одного родителя. Самый верхний узел (совет директоров, в нашем случае) родителя не имеет. Этот узел называется «корневым», или «корнем».
Вопросы о деревьях задают даже на собеседовании в Apple.
Двоичное дерево поиска
Двоичное дерево поиска похоже на дерево из примера выше, но строится по определенным правилам:
Давайте посмотрим на дерево, построенное по этим правилам:
Двоичное дерево поиска
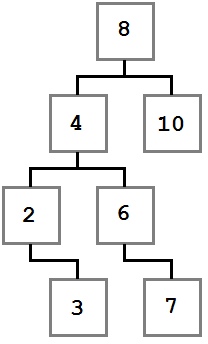
Обратите внимание, как указанные ограничения влияют на структуру дерева. Каждое значение слева от корня (8) меньше восьми, каждое значение справа — больше либо равно корню. Это правило применимо к любому узлу дерева.
Учитывая это, давайте представим, как можно построить такое дерево. Поскольку вначале дерево было пустым, первое добавленное значение — восьмерка — стало его корнем.
Рассмотрим подробнее первые шаги.
В первую очередь добавляется 8. Это значение становится корнем дерева. Затем мы добавляем 4. Поскольку 4 меньше 8, мы кладем ее в левого ребенка, согласно правилу 2. Поскольку у узла с восьмеркой нет детей слева, 4 становится единственным левым ребенком.
После этого мы добавляем 2. 2 меньше 8, поэтому идем налево. Так как слева уже есть значение, сравниваем его со вставляемым. 2 меньше 4, а у четверки нет детей слева, поэтому 2 становится левым ребенком 4.
Затем мы добавляем тройку. Она идет левее 8 и 4. Но так как 3 больше, чем 2, она становится правым ребенком 2, согласно третьему правилу.
Последовательное сравнение вставляемого значения с потенциальным родителем продолжается до тех пор, пока не будет найдено место для вставки, и повторяется для каждого вставляемого значения до тех пор, пока не будет построено все дерево целиком.
Класс BinaryTreeNode
Класс BinaryTreeNode представляет один узел двоичного дерева. Он содержит ссылки на левое и правое поддеревья (если поддерева нет, ссылка имеет значение null ), данные узла и метод IComparable.CompareTo для сравнения узлов. Он пригодится для определения, в какое поддерево должен идти данный узел. Как видите, класс BinaryTreeNode очень простой:
Класс BinaryTree
Кроме того, в классе есть ссылка на корневой узел дерева и поле с общим количеством узлов.
Метод Add
Добавление узла не представляет особой сложности. Оно становится еще проще, если решать эту задачу рекурсивно. Есть всего два случая, которые надо учесть:
Если дерево пустое, мы просто создаем новый узел и добавляем его в дерево. Во втором случае мы сравниваем переданное значение со значением в узле, начиная от корня. Если добавляемое значение меньше значения рассматриваемого узла, повторяем ту же процедуру для левого поддерева. В противном случае — для правого.
Метод Remove
Удаление узла из дерева — одна из тех операций, которые кажутся простыми, но на самом деле таят в себе немало подводных камней.
В целом, алгоритм удаления элемента выглядит так:
Первый шаг достаточно простой. Мы рассмотрим поиск узла в методе Contains ниже. После того, как мы нашли узел, который необходимо удалить, у нас возможны три случая.
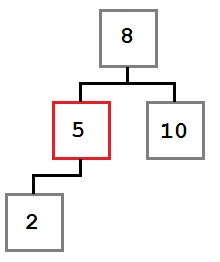
Случай 1: У удаляемого узла нет правого ребенка.
В этом случае мы просто перемещаем левого ребенка (при его наличии) на место удаляемого узла. В результате дерево будет выглядеть так:
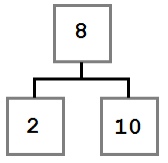
Случай 2: У удаляемого узла есть только правый ребенок, у которого, в свою очередь нет левого ребенка.
В этом случае нам надо переместить правого ребенка удаляемого узла (6) на его место. После удаления дерево будет выглядеть так:
Случай 3: У удаляемого узла есть первый ребенок, у которого есть левый ребенок.
В этом случае место удаляемого узла занимает крайний левый ребенок правого ребенка удаляемого узла.
Давайте посмотрим, почему это так. Мы знаем о поддереве, начинающемся с удаляемого узла следующее:
Мы дожны поместить на место удаляемого узел со значением, меньшим или равным любому узлу справа от него. Для этого нам необходимо найти наименьшее значение в правом поддереве. Поэтому мы берем крайний левый узел правого поддерева.
После удаления узла дерево будет выглядеть так:
Теперь, когда мы знаем, как удалять узлы, посмотрим на код, который реализует этот алгоритм.
Отметим, что метод FindWithParent (см. метод Contains ) возвращает найденный узел и его родителя, поскольку мы должны заменить левого или правого ребенка родителя удаляемого узла.
Мы, конечно, можем избежать этого, если будем хранить ссылку на родителя в каждом узле, но это увеличит расход памяти и сложность всех алгоритмов, несмотря на то, что ссылка на родительский узел используется только в одном.
Метод Contains
Метод Count
Метод Clear
Обход деревьев
Обходы дерева — это семейство алгоритмов, которые позволяют обработать каждый узел в определенном порядке. Для всех алгоритмов обхода ниже в качестве примера будет использоваться следующее дерево:
Пример дерева для обхода
Также, кроме описания поведения и алгоритмической сложности метода будет указываться порядок значений, полученный при обходе.
Метод Preorder (или префиксный обход)
При префиксном обходе алгоритм получает значение текущего узла перед тем, как перейти сначала в левое поддерево, а затем в правое. Начиная от корня, сначала мы получим значение 4. Затем таким же образом обходятся левый ребенок и его дети, затем правый ребенок и все его дети.
Префиксный обход обычно применяется для копирования дерева с сохранением его структуры.
Метод Postorder (или постфиксный обход)
При постфиксном обходе мы посещаем левое поддерево, правое поддерево, а потом, после обхода всех детей, переходим к самому узлу.
Постфиксный обход часто используется для полного удаления дерева, так как в некоторых языках программирования необходимо убирать из памяти все узлы явно, или для удаления поддерева. Поскольку корень в данном случае обрабатывается последним, мы, таким образом, уменьшаем работу, необходимую для удаления узлов.
Метод Inorder (или инфиксный обход)
Инфиксный обход используется тогда, когда нам надо обойти дерево в порядке, соответствующем значениям узлов. В примере выше в дереве находятся числовые значения, поэтому мы обходим их от самого маленького до самого большого. То есть от левых поддеревьев к правым через корень.
В примере ниже показаны два способа инфиксного обхода. Первый — рекурсивный. Он выполняет указанное действие с каждым узлом. Второй использует стек и возвращает итератор для непосредственного перебора.
Метод GetEnumerator
Продолжение следует
На этом мы заканчивает пятую часть руководства по алгоритмам и структурам данных. В следующей статье мы рассмотрим множества (Set).
Двоичные деревья поиска
Автор: Роман Акопов
Источник: RSDN Magazine #5-2003
Опубликовано: 22.05.2004
Исправлено: 10.12.2016
Версия текста: 1.0
Определение Двоичного Дерева Поиска (Binary Search Tree, BST)
Двоичным деревом поиска (ДДП) называют дерево, все вершины которого упорядочены, каждая вершина имеет не более двух потомков (назовём их левым и правым), и все вершины, кроме корня, имеют родителя. Вершины, не имеющие потомков, называются листами. Подразумевается, что каждой вершине соответствует элемент или несколько элементов, имеющие некие ключевые значения, в дальнейшем именуемые просто ключами. Обычно одной вершине соответствует один элемент, поэтому данные термины можно без потери смысла считать синонимами, хотя и надо помнить, что в некоторых реализациях это не так. В приведённых алгоритмах считается, что одной вершине соответствует только один элемент. Поэтому мы будем использовать понятия ключа вершины и данных вершины, подразумевая ключ и данные соответствующего вершине элемента. Мы так же будем понимать под вставкой вершины добавление вершины с указанным значением элемента и присвоение указателям на родителя и потомков корректных значений. Именно ключ используется во всех операциях сравнения элементов. Элемент может также содержать ассоциированные с ключом данные. На практике в качестве ключа может использоваться часть данных элемента. Ключ также может храниться как отдельное значение. ДДП позволяет выполнять следующие основные операции:
Двоичное дерево может быть логически разбито на уровни. Корень дерева является нулевым уровнем, потомки корня – первым уровнем, их потомки – вторым, и т.д. Глубина дерева это его максимальный уровень. Понятие глубины также может быть описано в терминах пути, то есть глубина дерева есть длина самого длинного пути от корня до листа, если следовать от родительской вершины до потомка. Каждую вершину дерева можно рассматривать как корень поддерева, которое определяется данной вершиной и всеми потомками этой вершины, как прямыми, так и косвенными. Поэтому о дереве можно говорить как о рекурсивной структуре. Эффективность поиска по дереву напрямую связана с его сбалансированностью, то есть с максимальной разницей между глубиной левого и правого поддерева среди всех вершин. Имеется два крайних случая – сбалансированное бинарное дерево (где каждый уровень имеет полный набор вершин) и вырожденное дерево, где на каждый уровень приходится по одной вершине. Вырожденное дерево эквивалентно связанному списку. Время выполнения всех основных операций пропорционально глубине дерева. Таким образом, скоростные характеристики поиска в ДДП могут варьироваться от O(log 2 N) в случае законченного дерева до O(N) – в случае вырожденного.
ДДП может быть использовано для реализации таких абстракций, как сортированный список, словарь (набор соответствий «ключ-значение»), очередь с приоритетами и так далее.
При реализации дерева помимо значения ключа (key) и данных также хранятся три указателя: на родителя (net), левого (left) и правого (right) потомков. Если родителя или потомка нет, то указатель хранит нулевое (NULL, NIL) значение.
Свойство упорядоченности двоичного дерева поиска
Если x – это произвольная вершина в ДДП, а вершина y находится в левом поддереве вершины x, то y.key = x.key. Из свойства следует, что если y.key == x.key, то вершина y может находиться как в левом, так и в правом поддереве относительно вершины x.
Необходимо помнить, что при наличии нескольких вершин с одинаковыми значениями ключа некоторые алгоритмы не будут работать правильно. Например, алгоритм поиска будет всегда возвращать указатель только на одну вершину. Эту проблему можно решить, храня элементы с одинаковыми ключами в одной и той же вершине в виде списка. В таком случае мы будем хранить в одной вершине несколько элементов, но данный случай в статье не рассматривается.
Это двоичное дерево поиска:
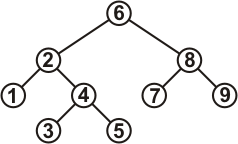
Рисунок 1.
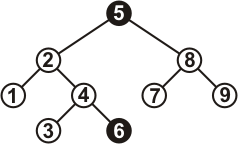
Рисунок 2.
Способы обхода ДДП
Есть три способа обхода: Прямой (preorder), Поперечный (inorder), Обратный (postorder).
На рисунке 3 порядок обхода вершин указан номерами, при этом предполагается, что сами вершины расположены так, что образуют ДДП.
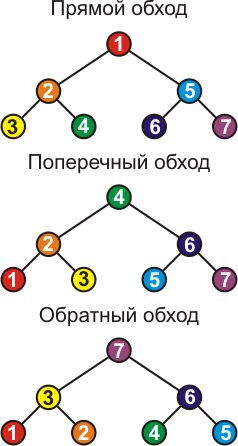
Рисунок 3.
Наиболее часто употребляется поперечный обход, так как во всех других способах обхода следующие друг за другом вершины не связаны никакими условиями отношения.
Поиск вершины в ДДП
Идея поиска проста. Алгоритм поиска в ДДП по своей природе рекурсивен. При его описании проще всего использовать понятие поддерева. Поиск начинается с корня дерева, который принимается за корень текущего поддерева, и его ключ сравнивается с искомым. Если они равны, то, очевидно, поиск закончен. Если ключ, который мы ищем, оказался больше текущего, то, очевидно, что нужная вершина находится в правом поддереве, иначе – в левом. Далее эта операция повторяется для правого или левого поддерева. В условном коде это можно описать так:
В прилагаемом исходном коде, написанном на паскале-подобном языке, все параметры передаются по значению. nodeParent, nodeTemp и node – это указатели на вершины, а Tree – само дерево, имеющее поле root, указатель на корень дерева.
Поиск вершины с минимальным и максимальным значением ключа
Вершины с минимальным и максимальным значением ключа можно найти, пройдясь по левым (правым) указателям от корня (пока не достигнем NIL). Возвращаемое значение – это указатель на вершину с минимальным (максимальным) значением ключа.
Нахождение следующей и предыдущей вершины в ДДП
Чтобы найти предыдущую и следующую вершину, надо снова вспомнить свойство упорядоченности. Рассмотрим это на примере функции TreeNext. Она учитывает два случая. Если правое поддерево не пусто, то вершина из правого поддерева с минимальным значением ключа и будет следующей. Если же правое поддерево пусто, тогда мы идём вверх, пока не найдём вершину, являющуюся левым потомком своего родителя. Этот родитель (если он есть) и будет следующей вершиной. Возвращаемое значение – это указатель на вершину с следующим (предыдущим) значеним ключа или NIL, если такой вершины нет.
Добавление вершины
Добавление вершины в ДДП сопряжено с некоторыми проблемами. После добавления ДДП должно сохранить свойство упорядоченности, а это значит, что вершину, куда попало добавлять нельзя. Поэтому, прежде чем вставлять вершину, необходимо подобрать для неё подходящее место, то есть такое место, после вставки в которое, дерево сохранит своё свойство упорядоченности. Говоря другими словами, нам нужно место после вершины с наибольшим ключом из всех меньших данного.
Удаление вершины
Проблемы возникают и при удалении. Нам необходимо сохранить свойство упорядоченности ДДП. При удалении возможны три случая: у удаляемой вершины нет потомков, у удаляемой вершины есть один потомок и у удаляемой вершины два потомка. Если потомков нет, то вершину можно просто удалить. Если потомок один, то удаляемую вершину можно “вырезать”, указав её родителю в качестве потомка единственного имеющегося потомка удаляемой вершины. Если же потомков два, требуются дополнительные действия. Нужно найти следующую за удаляемой (по порядку ключей) вершину, скопировать её содержимое (ключ и данные) в удаляемую вершину (она теперь никуда не удаляется физически, хотя логически исчезает) и удалить найденную вершину (у неё не будет левого потомка). Сначала функция TreeDelete ищет вершину, которую надо удалить, затем переменной nodeTemp присваивается указатель на существующего потомка удаляемой вершины (или NIL, если потомков нет). Далее вершина удаляется из дерева, при этом отдельно рассматриваются случаи: когда потомков нет и когда удаляемая вершина – это корень дерева. Возвращаемое значение – это указатель на удалённую вершину. На неё уже нет никаких ссылок в самом дереве, но она всё ещё занимает память. Момент её реального удаления зависит от используемых методов распределения памяти.
NIL, NULL и маленькие хитрости
Нередко алгоритмы, просто выглядящие на бумаге, становятся нагромождением сплошных конструкций if в реальной программе. Почему? Ответ очевиден: многие алгоритмы для работы с деревьями предполагают, что (NIL).parent == (NIL).left == (NIL).right == NIL. Вроде всё ясно и даже логично, но ведь во многих языках программирования NIL/NULL – это ноль. А обращение по нулевому адресу памяти чревато нехорошими вещами. Что же делать? Ведь мало того, что все эти if тормозят программу, в них легко запутаться! Решение просто: мы не будем использовать NIL! Действительно, алгоритмам совершенно всё равно, какое численное значение имеет NIL, главное, чтобы адрес любой реальной вершины в дереве не был ему равен. Поэтому вместо NIL мы будем использовать адрес переменной, проинициализированной особым образом. Я покажу это на языке С++, но думаю, этот пример можно будет перевести и на другие языки, хотя там, скорее всего, нет шаблонов, и придется пожертвовать типобезопасностью.
Теперь везде в классе CTree можно использовать переменную treeNil. Преимущества очевидны. Потратив каких-то двенадцать (3 * sizeof(CTree *)) байт памяти, мы упростили разработку и ускорили выполнение программы.
Основная проблема использования ДДП
Основной проблемой использования ДДП является то, что методы вставки и удаления вершин, гарантируя сохранение свойства упорядоченности, совершенно не способствуют оптимизации основных операций над ДДП. Например, если вставить в ДДП последовательность возрастающих или убывающих чисел, оно превратится, по сути, в двусвязный список, а основные операции будут занимать время, пропорциональное количеству вершин, а не его логарифму.
Таким образом, для получения производительности порядка O(log 2 N) нужно, чтобы дерево имело как можно более высокую сбалансированность (то есть имело возможно меньшую высоту). Обычно выделяются несколько типов сбалансированности. Полная сбалансированность, это когда для каждой вершины дерева количества вершин в левом и правом поддеревьях различаются не более чем на 1. К сожалению, такой сбалансированности трудно добиться на практике. Поэтому на практике используются менее жесткие виды сбалансированности. Например, русскими математиками Г. М. Адельсон-Вельским и Е.М.Ландисом были разработаны принципы АВЛ деревьев. В АВЛ деревьях для каждой вершины дерева глубины обоих поддеревьев различаются не более чем на 1. Еще одним “продвинутым” видом деревьев является так называемые красно-чёрные деревья. АВЛ деревья обеспечивают более высокую сбалансированность дерева, но затраты на их поддержание выше. Поскольку на практике разница в сбалансированности между этими двумя видами деревьев не высока, чаще используются красно-чёрные деревья.
Красно-чёрные деревья (Red-Black Tree, RB-Tree)
Итак, одним из способов решения основной проблемы использования ДДП являются красно-чёрные деревья. Красно-чёрные (название исторически связано с игральными картами, поскольку из них легко делать простые модели) деревья (КЧД) – это ДДП, каждая вершина которых хранит ещё одно дополнительное логическое поле (color), обозначающее цвет: красный или чёрный. Фактически, в КЧД гарантируется, что уровни любых двух листьев отличаются не более, чем в два раза. Этого условия оказывается достаточно, чтобы обеспечить скоростные характеристики поиска, близкие к O(log 2 N). При вставке/замене производятся дополнительные действия по балансировке дерева, которые не могут не замедлить работу с деревом. При описании алгоритмов мы будем считать, что NIL – это указатель на фиктивную вершину, и операции (NIL).left, (NIL).right, (NIL).color имеют смысл. Мы также будем полагать, что каждая вершина имеет двух потомков, и лишь NIL не имеет потомков. Таким образом, каждая вершина становится внутренней (имеющей потомков, пусть и фиктивных), а листьями будут лишь фиктивные вершины NIL.
Свойства КЧД
Пример КЧД с учётом наших положений приведен на рисунке 4. Учтите, что вершина 9 могла быть и красной, но в дальнейшем мы будем рассматривать только те деревья, у которых корень чёрный. Мы это сделаем для того, чтобы потомки корня могли иметь любой цвет.
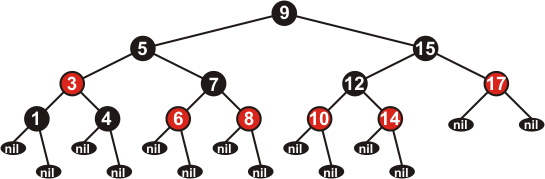
Рисунок 4.
Вращения
Операции вставки и удаления вершин в КЧД могут нарушать свойства КЧД. Чтобы восстановить эти свойства, надо будет перекрашивать некоторые вершины и менять структуру дерева. Для изменения структуры используются операции, называемые вращением. Возвращая КЧД его свойства, вращения так же восстанавливают сбалансированность дерева. Вращения бывают левые и правые, их суть показана на рисунке 5.
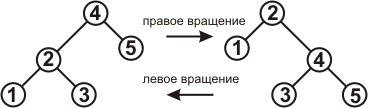
Рисунок 5.
Как видно, вращения, перемещая вершины, не нарушают свойства упорядоченности.
Добавление вершины в КЧД
Чтобы добавить вершину в КЧД, мы применяем процедуру TreeInsert для ДДП, красим вершину в красный цвет, а затем восстанавливаем свойства КЧД. Для этого мы перекрашиваем некоторые вершины и производим вращения.
Случай 1 (строки 12-15 и 34-37) показан на рисунке 6. Является ли вершина node правым или левым потомком своего родителя, значения не имеет.
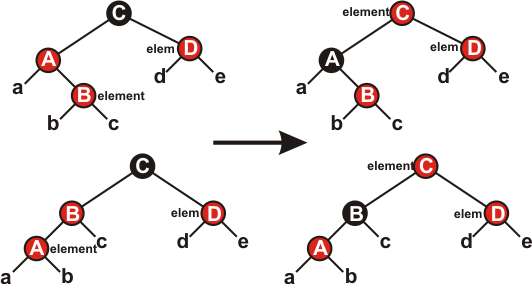
Рисунок 6.
Обе вершины (node и nodeTemp) – красные, а вершина node.nodeParent.nodeParent – чёрная. Перекрасим node.nodeParent и nodeTemp в чёрный цвет, а node.nodeParent.nodeParent – в красный. При этом число чёрных вершин на любом пути от корня к листьям остаётся прежним. Нарушение свойств КЧД возможно лишь в одном месте: вершина node.nodeParent.nodeParent может иметь красного родителя, поэтому надо продолжить выполнение цикла, присвоив node значение node.nodeParent.nodeParent.
В случаях 2 и 3 вершина nodeTemp – чёрная. Различаются случаи, когда вершина node является правым или левым потомком своего родителя. Если правым, то это случай 2 (строки 20-23 и 41-45). В этом случае производится левое вращение, которое сводит случай 2 к случаю 3, когда node является левым потомком своего родителя. Так как node и node.nodeParent – красные, после вращения количество чёрных вершин на путях от корня к листьям остается прежним.
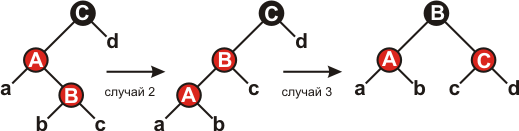
Рисунок 7.
Осталось рассмотреть случай 3: красная вершина node является левым потомком красной вершины node.nodeParent, которая, в свою очередь, является левым потомком node.nodeParent.nodeParent, правым потомком которой является nodeTemp. В этом случае достаточно произвести правое вращение и перекрасить две вершины. Цикл окончится, так как вершина node.nodeParent будет после этого чёрной.
Удаление вершины из КЧД
Удаление вершины немного сложнее добавления. Мы будем считать, что (NIL).color == BLACK, и будем считать операцию взятия цвета у указателя, равного NIL, допустимой операцией. Также мы будем считать допустимым присваивание (NIL).nodeParent, и будем считать данное присваивание имеющим результат. То есть при взятии значения (NIL).nodeParent мы получим ранее записанное значение. Функция RBTDelete подобна TreeDelete, но, удалив вершину, она вызывает процедуру RTBDeleteFixUp для восстановления свойств КЧД.
Рассмотрим, как процедура RBTDeleteFixUp восстанавливает свойства КЧД. Очевидно, что если удалили красную вершину, то, поскольку оба ее потомка чёрные, красная вершина не станет родителем красного потомка. Если же удалили чёрную вершину, то как минимум на одном из путей от корня к листьям количество чёрных вершин уменьшилось. К тому же красная вершина могла стать потомком красного родителя.
Процедура RBTDeleteFixUp применяется к дереву, которое обладает свойствами КЧД, если учесть дополнительную единицу черноты в вершине node (она теперь дважды чёрная, это чисто логическое понятие, и оно нигде фактически не сохраняется и логического типа для хранения цвета вам всегда будет достаточно) и превращает его в настоящее КЧД.
Что такое дважды чёрная вершина? Это определение может запутать. Формально вершина называется дважды чёрной, дабы отразить тот факт, что при подсчёте чёрных вершин на пути от корня до листа эта вершина считается за две черных. Если чёрная вершина была удалена, её черноту так просто выкидывать нельзя. Она на счету. Поэтому временно черноту удалённой вершины передали вершине node. В задачу процедуры RBTDeleteFixUp входит распределение этой лишней черноты. Они или будет передана красной вершине (и та станет чёрной) или после перестановок других чёрных вершин (дабы изменить их количество на пути от корня к листьям) будет просто выкинута.
В цикле (строки 3-67) дерево изменяется, и значение переменной node тоже изменяется, но сформулированное свойство остаётся верным. Цикл завершается, если:
Внутри цикла node указывает на дважды чёрную вершину, а nodeTemp – на её брата (другую вершину с тем же родителем). Поскольку вершина node дважды чёрная, nodeTemp не может быть NIL, поскольку в этом случае вдоль одного пути от node.nodeParent было бы больше чёрных вершин, чем вдоль другого. Четыре возможных случая показаны на рисунке ниже. Зелёным и синим, помечены вершины, цвет которых не играет роли, то есть может быть как черным, так и красным, но сохраняется в процессе преобразований.
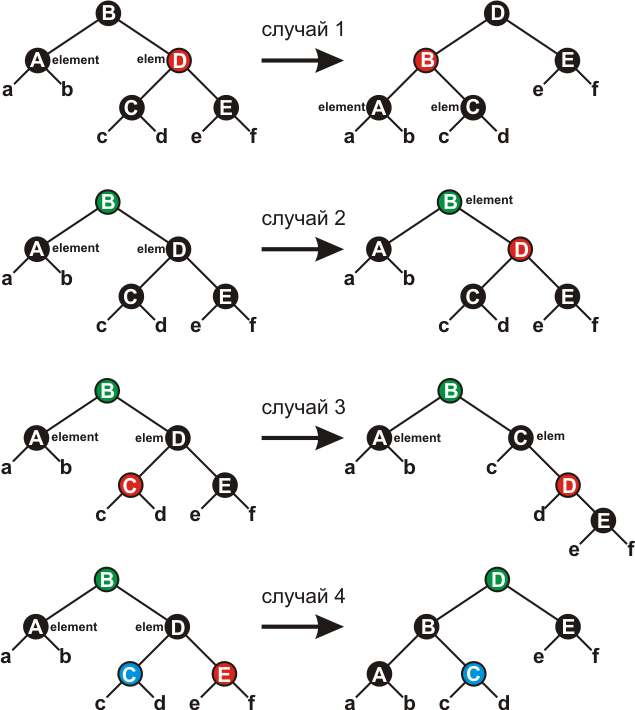
Рисунок 8
Случай 1 (строки 9-14 и 40-45) имеет место, когда вершина nodeTemp красная (в этом случае node.nodeParent чёрная). Так как оба потомка вершины nodeTemp чёрные мы можем поменять цвета nodeTemp и node.nodeParent и произвести левое вращение вокруг node.nodeParent не нарушая свойств КЧД. Вершина node остается дважды чёрной, а её новый брат – чёрным, так что мы свели дело к одному из случаев 2-4.
Случай 2 (строки 16-19 и 47-50). Вершина nodeTemp – чёрная, и оба её потомка тоже чёрные. В этом случае мы можем снять лишнюю чёрноту с node (теперь она единожды чёрная), перекрасить nodeTemp, сделав ёё красной (оба её потомка чёрные, так что это допустимо) и добавить черноту родителю node. Заметим, что если мы попали в случай 2 из случая 1, то вершина node.nodeParent – красная. Сделав её чёрной (добавление чёрного к красной вершине делает её чёрной), мы завершим цикл.
Сравнительные характеристики скорости работы различных структур данных
Чтобы всё сказанное до этого не казалось пустой болтовнёй, я в качестве заключения приведу сравнительные характеристики скорости работы различных структур данных (деревьев и массивов). Для измерения времени была использована функция WinAPI QueryPerfomanceCounter. Время пересчитано в микросекунды. В скобках приведена конечная глубина дерева. Тестирование проводилось на процессоре Intel Celeron Tualatin 1000MHz с 384Мб оперативной памяти. В качестве ключа использовалось число типа int (32-х битное целое со знаком), а в качестве данных число типа float (4-х байтное вещественное).
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Несортированный массив | Массив с постсортировкой |
|---|---|---|---|---|---|
| 1000 | 4943 (1000) | 535 (17) | 193 | 32 | 73 |
| 2000 | 20571 (2000) | 1127 (19) | 402 | 89 | 152 |
| 3000 | 65819 (3000) | 1856 (20) | 621 | 98 | 305 |
| 4000 | 82321 (4000) | 2601 (21) | 862 | 189 | 327 |
| 5000 | 126941 (5000) | 3328 (22) | 1153 | 192 | 461 |
| 6000 | 183554 (6000) | 4184 (22) | 1391 | 363 | 652 |
| 7000 | 255561 (7000) | 4880 (23) | 1641 | 452 | 789 |
| 8000 | 501360 (8000) | 5479 (23) | 1905 | 567 | 874 |
| 9000 | 1113230 (9000) | 6253 (24) | 2154 | 590 | 1059 |
| 10000 | 1871090 (10000) | 7174 (24) | 2419 | 662 | 1180 |
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Несортированный массив | Массив с постсортировкой |
|---|---|---|---|---|---|
| 1000 | 4243 | 108 | 136 | 1354 | 134 |
| 2000 | 19295 | 250 | 289 | 5401 | 286 |
| 3000 | 71271 | 391 | 448 | 25373 | 441 |
| 4000 | 79819 | 560 | 615 | 23861 | 607 |
| 5000 | 124468 | 759 | 787 | 38862 | 776 |
| 6000 | 180029 | 956 | 954 | 55303 | 941 |
| 7000 | 246745 | 1199 | 1165 | 75570 | 1111 |
| 8000 | 487187 | 1412 | 1307 | 98729 | 1330 |
| 9000 | 1062128 | 1906 | 1494 | 134470 | 1474 |
| 10000 | 1807235 | 2068 | 1719 | 154774 | 1688 |
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Несортированный массив | Массив с постсортировкой |
|---|---|---|---|---|---|
| 1000 | 308 | 419 | 2077 | 2047 | 2080 |
| 2000 | 639 | 876 | 13422 | 8046 | 8179 |
| 3000 | 1001 | 1372 | 25092 | 30902 | 18407 |
| 4000 | 1380 | 1831 | 32572 | 32473 | 32651 |
| 5000 | 1680 | 2286 | 50846 | 51001 | 50962 |
| 6000 | 2105 | 2891 | 73321 | 73114 | 73202 |
| 7000 | 2569 | 3514 | 99578 | 100059 | 99801 |
| 8000 | 3025 | 4384 | 129833 | 129897 | 130054 |
| 9000 | 3484 | 5033 | 164846 | 194361 | 164264 |
| 10000 | 4050 | 5690 | 203207 | 202979 | 202738 |
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Несортированный массив | Массив с постсортировкой |
|---|---|---|---|---|---|
| 1000 | 547 (25) | 548 (13) | 1800 | 34 | 362 |
| 2000 | 1133 (25) | 1171 (14) | 5534 | 70 | 734 |
| 3000 | 1723 (28) | 1905 (14) | 12065 | 150 | 1174 |
| 4000 | 2891 (28) | 2985 (15) | 20867 | 223 | 1626 |
| 5000 | 3604 (28) | 4024 (15) | 32927 | 248 | 1962 |
| 6000 | 4336 (29) | 4970 (15) | 44720 | 373 | 2537 |
| 7000 | 5196 (29) | 5794 (16) | 60723 | 443 | 2977 |
| 8000 | 6051 (30) | 6972 (16) | 77482 | 511 | 3485 |
| 9000 | 6994 (30) | 7519 (16) | 104219 | 590 | 3821 |
| 10000 | 9544 (31) | 10303 (16) | 118760 | 584 | 4408 |
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Несортированный массив | Массив с постсортировкой |
|---|---|---|---|---|---|
| 1000 | 181 | 136 | 159 | 1354 | 155 |
| 2000 | 406 | 307 | 347 | 5412 | 339 |
| 3000 | 653 | 494 | 551 | 12927 | 538 |
| 4000 | 925 | 702 | 765 | 23936 | 747 |
| 5000 | 1223 | 949 | 1024 | 37861 | 962 |
| 6000 | 1532 | 1142 | 1216 | 55124 | 1185 |
| 7000 | 1893 | 1494 | 1453 | 75628 | 1403 |
| 8000 | 2477 | 1833 | 1679 | 98802 | 1631 |
| 9000 | 2943 | 2390 | 1994 | 125570 | 1858 |
| 10000 | 3395 | 2937 | 2228 | 154791 | 2108 |
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Несортированный массив | Массив с постсортировкой |
|---|---|---|---|---|---|
| 1000 | 469 | 517 | 1149 | 2014 | 1195 |
| 2000 | 995 | 1079 | 4381 | 8054 | 4387 |
| 3000 | 1557 | 1756 | 9673 | 18191 | 9639 |
| 4000 | 2272 | 2424 | 17071 | 32451 | 17105 |
| 5000 | 3070 | 3019 | 27380 | 50665 | 26954 |
| 6000 | 3528 | 3618 | 39294 | 72996 | 39227 |
| 7000 | 4322 | 4542 | 53255 | 99402 | 53309 |
| 8000 | 5299 | 5531 | 71406 | 129964 | 70766 |
| 9000 | 6180 | 6553 | 89583 | 164943 | 89935 |
| 10000 | 7527 | 7797 | 112190 | 202993 | 111439 |
Постоянно сортированный массив – это массив, в который элементы вставляются так, что бы он сохранял свойство упорядоченности. Массив с постсортировкой – это массив, в который сначала вставляются все элементы, а потом он сортируется алгоритмом быстрой сортировки. Данные таблицы, безусловно, не являются истиной в последней инстанции, но позволят вам прикинуть, какая из структур данных будет наиболее производительна в вашей программе, учитывая предполагаемую вероятность операций вставки, удаления и поиска. Так, например, массив с постсортировкой является весьма привлекательным по производительности, но совершенно не подходит для комплексных работ, так как предполагает фиксированный порядок действий – сначала только добавление элементов, а после использование полученной информации. Другие структуры данных лишены этого недостатка. Для большого числа (порядка 10 000) случайных элементов время поиска в ДДП и КЧД становится практически одинаковым. Как следствие, можно реализовать более простые алгоритмы, исходя из некоторых свойств входных данных. С другой стороны, в крайнем случае (возрастающие элементы) ДДП отстают от КЧД на несколько порядков. Постоянно сортированный массив является абсолютным победителем по скорости, но не имеет естественной поддержки отношений родитель-ребёнок. Если они вам нужны, придётся реализовывать их поддержку самостоятельно. Также надо всегда помнить, что при количестве элементов порядка тысячи, асимптотические показатели скорости ещё не вполне вступили в силу и теоретически более быстрые структуры данных на практике могут оказаться более медленными. Так, например, скорость поиска в КЧД и массиве с пресортировкой до 5000-7000 практически одинакова. Так же надо заметить, что тестирование производилось на объектах относительно малого размера (8 байт), сравнимого с размером указателя (4 байта). Все виды массивов сортированных подразумевают весьма интенсивное копирование элементов, в то время как деревья работают с указателями. При размере элемента, на порядки превышающем размеры указателя, акценты сместятся весьма значительно. Например, ниже приведены результаты испытания с ключом типа int (32-x битное целое) и битовыми данными размером в 256 байт.
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Не сортированный массив | Массив с постсортировкой |
|---|---|---|---|---|---|
| 1000 | 5868 (1000) | 1663 (17) | 1430 | 1154 | 1035 |
| 2000 | 140888 (2000) | 3694 (19) | 3476 | 2460 | 2808 |
| 3000 | 368748 (3000) | 5815 (20) | 5372 | 3848 | 4382 |
| 4000 | 721328 (4000) | 7271 (21) | 7274 | 5175 | 6035 |
| 5000 | 1208373 (5000) | 9349 (22) | 9247 | 6670 | 7619 |
| 6000 | 1752135 (6000) | 11395 (22) | 11046 | 7778 | 9168 |
| 7000 | 2501167 (7000) | 13503 (23) | 13327 | 9378 | 10764 |
| 8000 | 3334948 (8000) | 15753 (23) | 18222 | 12560 | 15267 |
| 9000 | 4266560 (9000) | 21600 (24) | 20564 | 15391 | 17430 |
| 10000 | 5421499 (10000) | 24105 (24) | 24064 | 17152 | 19341 |
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Не сортированный массив | Массив с постсортировкой |
|---|---|---|---|---|---|
| 1000 | 4289 | 132 | 242 | 1621 | 230 |
| 2000 | 134074 | 303 | 605 | 6903 | 530 |
| 3000 | 359985 | 457 | 961 | 24268 | 806 |
| 4000 | 706129 | 787 | 1336 | 27610 | 1121 |
| 5000 | 1183405 | 959 | 1736 | 44660 | 1516 |
| 6000 | 1730699 | 1116 | 2138 | 69068 | 1841 |
| 7000 | 2462759 | 1344 | 2494 | 103158 | 2251 |
| 8000 | 3293519 | 1565 | 2871 | 159274 | 2617 |
| 9000 | 4215750 | 1840 | 3284 | 278697 | 2923 |
| 10000 | 5361524 | 2060 | 3698 | 513268 | 3303 |
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Не сортированный массив | Массив с постсортировкой |
|---|---|---|---|---|---|
| 1000 | 502 | 583 | 115640 | 131837 | 186703 |
| 2000 | 1181 | 1152 | 1604342 | 1574484 | 1592896 |
| 3000 | 1602 | 1580 | 4616940 | 4653355 | 4604626 |
| 4000 | 2075 | 2537 | 8966113 | 8999484 | 8978279 |
| 5000 | 2689 | 3007 | 14848795 | 14851393 | 14822206 |
| 6000 | 3574 | 3836 | 21572736 | 21473162 | 21676597 |
| 7000 | 4129 | 4432 | 30384061 | 29938188 | 30409709 |
| 8000 | 4898 | 5424 | 39013182 | 39342862 | 39341616 |
| 9000 | 5086 | 6368 | 50197296 | 49946077 | 50320092 |
| 10000 | 6279 | 6372 | 63020912 | 62049584 | 62564125 |
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Не сортированный массив | Массив с постсортировкой |
|---|---|---|---|---|---|
| 1000 | 1903 (24) | 2072 (12) | 57991 | 1418 | 5448 |
| 2000 | 4532 (25) | 4739 (14) | 479463 | 3107 | 13907 |
| 3000 | 7747 (26) | 7819 (15) | 1727433 | 4992 | 22440 |
| 4000 | 10348 (29) | 10664 (15) | 3616654 | 6733 | 33905 |
| 5000 | 13064 (29) | 13652 (16) | 6141684 | 8314 | 43768 |
| 6000 | 16530 (31) | 16713 (16) | 9214638 | 10191 | 53619 |
| 7000 | 19305 (31) | 19642 (16) | 12981887 | 11904 | 61301 |
| 8000 | 23140 (32) | 23329 (16) | 17388765 | 13785 | 75968 |
| 9000 | 26051 (32) | 26378 (16) | 21935279 | 15335 | 92007 |
| 10000 | 29450 (32) | 29448 (16) | 27053495 | 17075 | 90155 |
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Не сортированный массив | Массив с постсортировкой |
|---|---|---|---|---|---|
| 1000 | 185 | 150 | 266 | 1613 | 274 |
| 2000 | 695 | 359 | 719 | 6974 | 724 |
| 3000 | 1044 | 586 | 1193 | 15561 | 1245 |
| 4000 | 2186 | 823 | 1694 | 27675 | 1703 |
| 5000 | 2701 | 1106 | 2234 | 44905 | 2314 |
| 6000 | 3898 | 1496 | 2874 | 71549 | 2871 |
| 7000 | 4883 | 1889 | 3464 | 109554 | 3371 |
| 8000 | 4186 | 2183 | 4060 | 165605 | 4077 |
| 9000 | 6760 | 2771 | 4696 | 281860 | 4622 |
| 10000 | 7291 | 3201 | 5372 | 514893 | 5384 |
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Не сортированный массив | Массив с постсортировкой |
|---|---|---|---|---|---|
| 1000 | 1235 | 1115 | 54929 | 111088 | 62794 |
| 2000 | 3042 | 2978 | 557875 | 1596298 | 558580 |
| 3000 | 4641 | 4703 | 1837401 | 4730623 | 1841029 |
| 4000 | 7531 | 6494 | 3830510 | 9008129 | 3833983 |
| 5000 | 9497 | 8788 | 6675616 | 14599142 | 6626964 |
| 6000 | 12018 | 10922 | 10270460 | 21832592 | 10315160 |
| 7000 | 14605 | 14376 | 14808484 | 29779691 | 14618091 |
| 8000 | 15876 | 16070 | 19927348 | 39932636 | 19946118 |
| 9000 | 20043 | 19079 | 25347571 | 49928153 | 25384886 |
| 10000 | 22117 | 21860 | 32049086 | 61766884 | 32072537 |