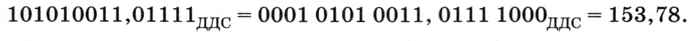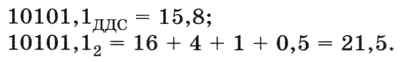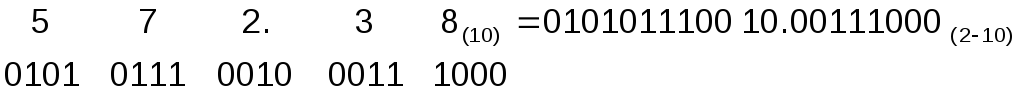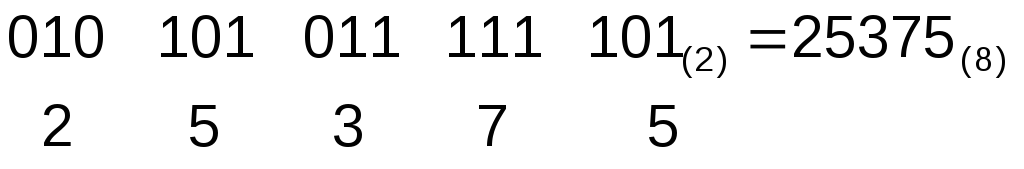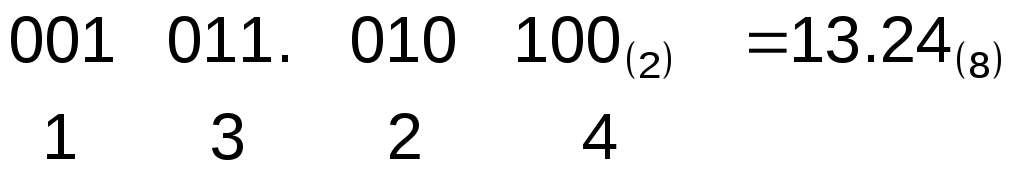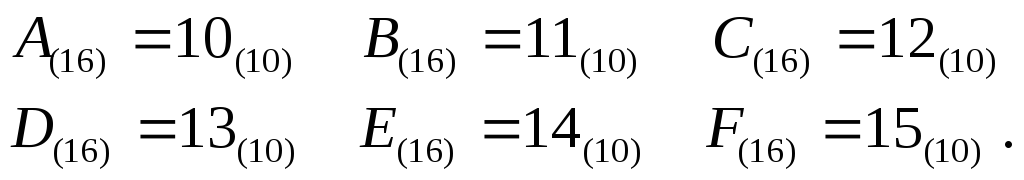что такое двоично десятичная система счисления
Содержание урока
§14. Другие системы счисления
Двоично-десятичная система счисления
Двоично-десятичная система счисления
Существует ещё один простой способ записи десятичных чисел с помощью цифр 0 и 1. Этот способ называется двоично-десятичной системой (ДДС), это нечто среднее между двоичной и десятичной системами. На английском языке такое кодирование называется binary coded decimal (BCD) — десятичные числа, закодированные двоичными цифрами.
В ДДС каждая цифра десятичного числа записывается двоичными знаками. Но среди цифр 0-9 есть такие, которые занимают 1, 2, 3 и 4 двоичных разряда. Чтобы запись числа была однозначной и не надо было искать границу между цифрами, на любую цифру отводят 4 бита. Таким образом, 0 записывается как 0000, а 9 — как 1001. Например:
При обратном переводе из ДДС в десятичную систему надо учесть, что каждая цифра занимает 4 бита, и добавить недостающие нули:
Важно помнить, что запись числа в ДДС не совпадает с его записью в двоичной системе:
Использование ДДС дает следующие преимущества:
• двоично-десятичный код очень легко переводить в десятичный, например, для вывода результата на экран;
• просто выполняется умножение и деление на 10, а также округление;
• конечные десятичные дроби записываются точно, без ошибки, так что вычисления в ДДС (вместо двоичной системы) дадут тот же результат, что и ручные расчёты человека «на бумажке»; поэтому ДДС используется в калькуляторах.
Есть, однако, и недостатки:
• хранение чисел в ДДС требует больше памяти, чем стандартный двоичный код;
• усложняются арифметические операции.
Следующая страница 
Cкачать материалы урока
Системы счисления, двоичная десятичная система счисления и числа
Системы счисления
Система счисления – одно из ключевых понятий в информатике, которое надо знать при изучении информационных технологий. Это основа, на базе которой строится всё остальное. Без понимания, что это такое, в будущем вам будет достаточно тяжело. Поэтому, самое время разобраться, что из себя представляет система счисления.
Что за зверь
Если говорить простыми словами, то система счисления – это способ записи чисел. Числа пишутся и обозначаются через знаки. Эти знаки называются цифрами. Все мы их уже прекрасно знаем – это 1, 2, 3, 4, 5 и так далее до бесконечности. Это арабские цифры, к которым мы все привыкли. Но есть и римские. Чаще всего мы встречаем вот эти римские цифры: I, V, X. Но есть ещё и вот такие: L, M. У нас они применяются, но гораздо реже, чем арабские цифры. Отсюда мы делаем вывод, что числа систем счисления бывают двух видов:
Также бывает позиционная и непозиционная система счисления. В первой итоговое количество чисел зависит от позиции, где стоит цифра. В непозиционной такого правила нет. Приведём пример. Возьмём число 11 и II. В первом случае мы используем арабские цифры, во втором – римские. 11 – это позиционная система счисления, где первая 1-ца показывает десятки, а вторая – единицу. В конце мы получаем итоговое число – одиннадцать. То есть, итог у нас зависит от того, на какой позиции стояли цифры. Поэтому такая система и называется позиционной.
Что же с II? Это пример непозиционной системы. Здесь мы видим, что I – это один. А II означает два, так как стоят две «палочки» и итоговое значение не зависит от позиции цифры в числе. Поэтому система непозиционная.
Надеемся, здесь всё понятно. Время перейти к примерам посложнее.
Возьмём числа 819, 595, 910. Рассматриваемой цифрой у нас будет девятка. В первом варианте 819 она стоит на последней позиции, а значит играет роль обычной девятки. В 595 девятка стоит на втором месте между пятёрками. Здесь она играет роль десятых (90), обозначая 95 – девяносто пять. В третьем числе 910 она стоит на первом месте, обозначая сотые (900), поэтому читается как «девять сот». Это ещё один пример позиционной системы счисления.
Возьмём непозиционную систему. Например, XXV, XVI, XIV. Рассматриваемое число – V. Посмотрите внимательно. Куда бы мы не поставили нашу V, она всегда будет обозначать пять единиц. А значит, итоговое значение не будет зависеть от позиции.
Возникает вопрос: как тогда удобнее считать? Как вы заметили, при сложении, умножении, делении, вычитании, мы применяем позиционные числа систем счисления.То есть, 12, 492, 3123 и так далее. Это неспроста. Выполнять математические операции с такими числами гораздо проще. Можно складывать и умножать в столбик, так проще делать операции деления и вычитания. С римскими гораздо тяжелее. По этой причине римские числа чаще применяются для обозначения времени. Например, XV лет до нашей эры. Тут можете просто заглянуть в учебник по истории, где римские цифры будут почти в каждой теме.
Слышал про разряд – что это такое
При работе с числами есть такое понятие, как разряд. Здесь совсем всё просто. Разряд — это позиция цифры, которое оно занимается в числе. А разрядность числа – то количество цифр, которые находятся в числе. Например, 48 – двухразрядное число, 987412 — шестиразрядное число, 127501750174 – двенадцатиразрядное число. Как мы это определили? А вы посчитайте количество цифр в числе и сами поймёте. В самих числах разряды считаются с правой стороны налево. Например, число 841. Единица находится в первом разряде. Четвёрка – во втором. Восьмёрка – в третьем. Думаем, принцип вы поняли.
Двоичная системы счисления
Двоичная система счисления – это система, в которой применяют только две цифры 0 (ноль) и 1 (единица). Двоичная система счисления во многом связана с десятичной системой счисления. Для простоты понимания двоичной системы, начнём с десятичной, так как в жизни мы используем её чаще всего.
В десятичной системе счисления мы применяем десять цифр. Это 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Когда мы доходим до последнего числа 9, то мы переходим на новый разряд – десяток. Счёт начинается с 10 и продолжается дальше 11, 12, 13 и так далее. Когда мы опять доходим до 9-ки в последнем числе разряда, в данном случае до 99, то мы переходим на сотни. Счёт начинается со ста – 100 и продолжается 101, 102, 103 и так далее. Снова доходим до последнего числа разряда сотен, 999, прибавляем 1 и начинается разряд тысяч – 1000, 1001, 1002 и далее. Так до бесконечности. Следовательно, последними цифрами в разряде десятка, сотни, тысячи являются 99, 999, 999 соответственно.
Двоичная система счисления точно такая же, как десятичная. Отличие лишь в том, что в ней есть только два числа – 0 и 1. Других цифр в этой системе нет. В каждом разряде есть свой предел. Для простоты понимания и решения разных задач, часто двоичную систему переводят в десятичную. Это выгляди так:
| Двоичная система счисления | Десятичная система счисления |
| 0 | Ноль |
| 1 | Один |
| 10 | Два |
| 11 | Три |
| 100 | Четыре |
| 101 | Пять |
| 110 | Шесть |
| 111 | Семь |
| 1000 | Восемь |
| 1001 | Девять |
Двоичная система счисления
Двоичная система счисления одна из самых распространённых в мире. Дело в том, что на ней работают все компьютеры и любая техника, которая выполняет вычисление. Они оперируют нулями и единицами. Почему не применяют десятичную систему? Это гораздо труднее. Зачем делать вычисления с огромными числами, когда можно создать систему для вычисления только двух чисел – нуля и единицы. По этой причине двоичная система применяется в любой вычислительной технике.
Теперь вы знаете, какие бывают системы счисления, числа систем счисления, что такое двоичная система счисления и десятичная система счисления. Отметим, что также бывает восьмеричная и шестнадцатеричная система счисления. Но, об этом позже. Рекомендуем для начала разобраться в двоичной и десятичной системах, а потом можно пойти и дальше.
2.2.3. Двоично-десятичная система счисления
Эта система имеет основание S = 10, но каждая цифра изображается четырехразрядным двоичным числом, называемым тетрадой. Обычно данная система счисления используется в ЭВМ при вводе и выводе информации. Однако в некоторых типах ЭВМ в АЛУ имеются специальные блоки десятичной арифметики, выполняющие операции над числами в двоично-десятичном коде. Это позволяет в ряде случаев существенно повышать производительность ЭВМ.
Например, в автоматизированной системе обработки данных чисел много, а вычислений мало. В этом случае операции, связанные с переводом чисел из одной системы в другую, существенно превысили бы время выполнения операций по обработке информации.
Перевод чисел из десятичной системы в двоично-десятичную весьма прост и заключается в замене каждой цифры двоичной тетрадой.
Записать десятичное число 572.38(10)в двоично-десятичной системе счисления.
Обратный перевод также прост: необходимо двоично-десятичное число разбить на тетрады от точки влево (для целой части) и вправо (для дробной), дописать необходимое число незначащих нулей, а затем каждую тетраду записать в виде десятичной цифры.
Записать двоично-десятичное число 10010.010101(2-10)в десятичной системе счисления.
Перевод чисел из двоично-десятичной в двоичную систему осуществляется по общим правилам, описанным выше.
2.3. Восьмеричная система счисления
В восьмеричной системе счисления употребляются всего восемь цифр, т.е. эта система счисления имеет основание S = 8. В общем виде восьмеричное число выглядит следующим образом:

где 
Восьмеричная система счисления не нужна ЭВМ в отличие от двоичной системы. Она удобна как компактная форма записи чисел и используется программистами (например, в текстах программ для более краткой и удобной записи двоичных кодов команд, адресов и операндов). В восьмеричной системе счисления вес каждого разряда кратен восьми или одной восьмой, поэтому восьмиразрядное двоичное число позволяет выразить десятичные величины в пределах 0-255, а восьмеричное охватывает диапазон 0-99999999 (для двоичной это составляет 27 разрядов).
Двоичное число 10101011111101(2)записать в восьмеричной системе счисления.
Двоичное число 1011.0101(2) записать в восьмеричной системе счисления.
Перевод из восьмеричной системы счисления в двоичную осуществляется путем представления каждой цифры восьмеричного числа трехразрядным двоичным числом (триадой).
2.4. Шестнадцатеричная система счисления
Эта система счисления имеет основание S = 16. В общем виде шестнадцатеричное число выглядит следующим образом:

где 
Для перевода числа из двоичной системы счисления в шестнадцатеричную необходимо разбить это число влево и вправо от точки на тетрады и представить каждую тетраду цифрой в шестнадцатеричной системе счисления.
Двоичное число 10101011111101(2)записать в шестнадцатеричной системе.
Двоичное число 11101.01111(2)записать в шестнадцатеричной системе.
Для перевода числа из шестнадцатеричной системы счисления в двоичную, необходимо, наоборот, каждую цифру этого числа заменить тетрадой.
В заключение следует отметить, что перевод из одной системы счисления в другую произвольных чисел можно осуществлять по общим правилам, описанным в разделе “Двоичная система счисления”. Однако на практике переводы чисел из десятичной системы в рассмотренные системы счисления и обратно осуществляются через двоичную систему счисления.
Кроме того, следует помнить, что шестнадцатеричные и восьмеричные числа – это только способ представления больших двоичных чисел, которыми фактически оперирует процессор. При этом шестнадцатеричная система оказывается предпочтительнее, поскольку в современных ЭВМ процессоры манипулируют словами длиной 4, 8, 16, 32 или 64 бита, т.е. длиной слов, кратной 4. В восьмеричной же системе счисления предпочтительны слова, кратные 3 битам, например слова длиной 12 бит (как в PDP-8 фирмы DEC).
Основные системы счисления применяемые в станках с ЧПУ и не только
Система счисления – это коды, которые используются для представления чисел числовыми знаками (цифрами). Наибольшее распространение получили позиционные системы счисления. В них запись произвольного числа А, имеющего основание m, представляется в виде полинома:
Здесь а – одна из цифр системы, m – основание системы, n – номер разряда;
При работе с системой счисления основание в большинстве случаев не пишут, а число записывается перечислением всех коэффициентов (символов) полинома:
Запятая, отделяющая дробную часть от целой, используется для фиксации значения каждого разряда в данной последовательности цифр.
Десятичная система счисления
Десятичная система счисления – одна из наиболее распространенных. Ее основание – 10. Использует она десять символов 0, 1, 2, …, 9. Возникновение десятичной системы счисления, согласно историческим сведениям, связано с количеством пальцев на руках.
В десятичной системе цифры 3807,45 представляют собой запись полинома:
в сокращенном виде.
При обычной записи в данной системе указываются только коэффициенты. Однако предполагают при этом, что их вес (значимость) определяется разрядом и различный, занимаемым данной цифрой (коэффициентом). Десятичная система не очень хорошо подходит для реализации в вычислительной техники. Это вызвано тем, что выполнение элемента с десятью различимыми состояниями довольно сложная техническая задача.
Унитарная система счисления
Здесь все проще – она имеет только один цифровой знак – 1. В этой системе можно обрабатывать только целые числа, которые будут представлены набором единиц. Например, число 2 будет представлено как 11, а число 17 как 11111111111111111. Унитарная система счисления очень проста и легко реализуемая – это плюс, но уж очень громоздкая – это минус. Ранее ее активно использовали для записей нужного количества импульсов на барабанах и магнитных лентах. Но из-за громоздкости она не получила широкого применения, ведь необходимо очень много символов для представления числа 4552/10 – 1111…1111…1111…
Другие позиционные системы счисления
Все другие позиционные системы счисления строятся по принципу десятичной системы счисления. Восьмеричная — использует восемь цифр m = 8 и на этом основании строится ее поленом, четверичная использует m = 4, пятеричная m = 5:
Двоичная система счисления
В двоичной системе счисления основание m = 2 и используются всего два символа – 1 и 0.Число в двоичной системе записывают полиномом, который может иметь только два значения – один или ноль. Например:
Использование двоичной системы счисления отлично подходит для устройств, имеющих два состояния. Также благодаря простоте выполнения операций арифметических и своей экономичности получила широкое распространение в автоматике и, соответственно, в вычислительной технике.
Перевод чисел из одной системы счисления в другую
Наиболее простым переводом считают перевод чисел восьмеричного счисления в двоичный, и наоборот. Такой подход довольно широко распространен в вычислительной технике. Для перевода восьмеричного числа в двоичное, его заменяют аналогичным трехразрядным числом (триадой), представленным в двоичном коде, как показано ниже:
Для обратного перевода (из двоичного в восьмеричный), необходимо разделить двоичный код на триады и заменить их восьмеричными цифрами. Если же крайняя правая или левая триады неполные, то нужно будет дописать недостающие нули.
Пример. Нужно перевести восьмеричное число 34,5/8 в двоичное. Для этого разбиваем число на отдельные цифры 3, 4, 5 и заменяем их эквивалентными триадами двоичного кода и в итоге получаем 011 100, 101. Очень часто нули в начале и конце записи не пишут, поэтому вполне можно встретить и такую запись 11100,101.
Еще один пример для перевода двоичного числа 11 010 111, 110 101 в восьмеричное:
Для преобразования целых чисел из одной системы счисления в другую, их последовательно делят на основание системы в которую они переводятся до получения минимального значения. В результате получаются остатки от деления и полученное минимальное значение, которые читаются в обратном порядке, как показано на примерах ниже:
Двоично-кодированные системы счисления
Определенное неудобство двоичной кодировки заключается в ее громоздкости. Например, количество цифр двоичного кода примерно в 13,3 раза больше, чем такое же число в представлении десятичным кодом. Именно из-за этого в технике довольно часто используют смешанные системы кодирования, такие как двоично-шестнадцатеричную, двоично-восьмеричную, двоично-десятичную. При смешанном кодировании объединяют достоинства нескольких систем, а именно – емкость (для шестнадцатеричных, восьмеричных и десятичных) и двоичное изображение цифр при использовании двоичного кодирования.
В двоично-десятичном коде каждая цифра десятичного числа (0, 1, 2, …,9) записывается двоичным кодом. Для этого используют двоичные разряды – тетрады:
Итак, двоично-десятичный код по существу является десятичным, а по форме двоичным. Ранее такие коды наиболее часто применялись для записи на перфоленты.
Рассмотренная выше двоично-десятичная система еще носит названия взвешенного двоично-десятичного кода 8421. Удобство данного кода хорошее, но имеется один недостаток, а именно – обрабатываться могут не только цифры 0…9, но и числа 10…15, которые используют не всегда и их приходится исключать.
Разработано большое количество кодов с другими наборами весов по разрядам – 2421, 5211, 7421 и многие другие. Также существуют коды, у которых присутствуют отрицательные веса в некоторых разрядах: (6)(4)(-2)(-1) и другие.
Также довольно часто используют для изображения в двоично-десятичных системах десятичных цифр комбинаторные коды, такие как – код Грея однопеременный, 2 из 5, 3 из 5 и другие.
Двоично-десятичная система счисления



В вычислительных системах часто используют комбинированную систему – двоично-десятичную систему счисления, облегчающую запись больших чисел с применением двоичного кода. Представляя каждую десятичную цифру совокупностью из четырех разрядов (тетрад), можно получить комбинированную систему счисления, которая обладает достоинствами двоичной системы и удобством десятичной. В ЭВМ наибольшее применение нашли системы кодирования 8421, 2421, 8421+3.
В двоично-десятичной системе каждая десятичная цифра представляется двоичным эквивалентом.
Примеры:
1. Число 197(10) в десятично-двоичной системе имеет вид
2. Число 24(10) представляется как 0010 0100(2-10), а 50610 как 0101 0000 01102-10
Недостатки. Недостатком этой системы является её избыточность для чисел 7 и менее (недоиспользуются многие двоичные разряды). Для устранения этого недостатка в ЭВМ используют восьмеричную систему счисления.