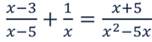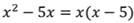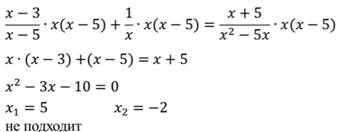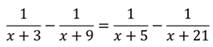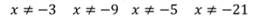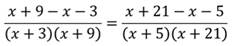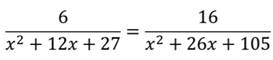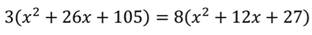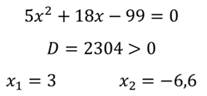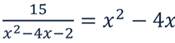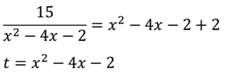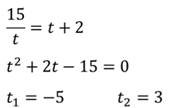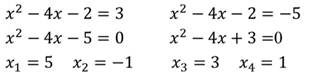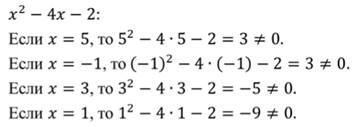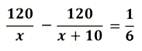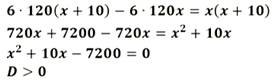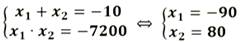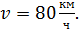что такое дробно рациональное уравнение

Что поможет в решении:

Ты можешь записаться на онлайн-уроки по математике для учеников 1-11 классов!

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Как решать уравнения с дробями

А теперь еще несколько способов, которые пригодятся ребенку на уроках математики.

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

А вот и полезные видео для закрепления материала:

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

Пример 2. Найти корень уравнения

Пример 3. Решить дробное уравнение:

Если x = 3 — знаменатель тоже равен нулю.

Если нужно решить уравнение с дробями быстро — поможет онлайн-калькулятор дробей. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

Источник

Дробные рациональные уравнения

Урок 12. Алгебра 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Дробные рациональные уравнения»

· найти общий знаменатель дробей, входящих в уравнение;

· умножить обе части уравнения на общий знаменатель;

· решить получившееся целое уравнение;

· исключить из корней те, которые обращают общий знаменатель в ноль.

Знаменатель дроби, стоящей в правой части уравнения, можно разложить на множители, тогда найдем общий знаменатель:

Умножим на него обе части уравнения, получим уравнение:

Проверим, x=5 обращает общий знаменатель в ноль, а x=-2 знаменатель не обращает в ноль, значит x=-2 является корнем данного дробного рационального уравнения.

Получили корень x=-2.

Найдём область допустимых значений переменной:

Приведём к общему знаменателю дроби:

Получим целое уравнение:

Преобразовав его, получаем квадратное уравнение:

Так как корни не входят в область допустимых значений, значит оба числа являются корнями исходного дробного рационального уравнения.

Решаем по алгоритму:

Осуществим обратную подстановку и решим полученные квадратные уравнения:

Проверим найденные корни:

Ни при каком из полученных значений знаменатель не обращается в ноль. Значит, данное дробное рациональное уравнение имеет 4 корня.

Больших вычислений требует проверка. Каждый корень нужно подставлять в уравнение.

От автобусной остановки отъехал автобус до аэропорта, находящегося на расстоянии 120 км. Один из пассажиров автобуса опоздал к отправлению на 10 минут, и решил поехать на такси. Автобус и такси приехали в аэропорт одновременно. Нужно найти скорость автобуса, если известно, что скорость такси на 10 км/ч больше.

Пусть х — скорость автобуса, тогда (х + 10) — скорость такси. Выразим время движения обоих транспортных средств и составим уравнение:

Решим полученное дробное рациональное уравнение:

Получаем скорость автобуса

Источник

Дробно рациональные уравнения

Для того, чтобы решить дробно рациональное уравнение, надо вспомнить, что такое ОДЗ и когда оно возникает.

ОДЗ – область допустимых значений переменной.

В выражении вида f ( x ) g ( x ) = 0

ОДЗ: g ( x ) ≠ 0 (знаменатель дроби не может быть равен нулю).

Алгоритм решения дробно рационального уравнения:

Пример решения дробного рационального уравнения:

Решить дробно рациональное уравнение x 2 − 4 2 − x = 1.

Решение:

Будем действовать в соответствии с алгоритмом.

Переносим единичку в левую часть, записываем к ней дополнительный множитель, чтобы привести оба слагаемых к одному общему знаменателю:

x 2 − 4 2 − x − 1 \ 2 − x = 0

x 2 − 4 2 − x − 2 − x 2 − x = 0

x 2 − 4 − ( 2 − x ) 2 − x = 0

x 2 − 4 − 2 + x 2 − x = 0

Первый шаг алгоритма выполнен успешно.

Обводим в рамочку ОДЗ, не забываем про него: x ≠ 2

x 2 + x − 6 = 0 – Квадратное уравнение. Решаем через дискриминант.

D = b 2 − 4 a c = 1 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 1 + 24 = 25

D > 0 – будет два различных корня.

x 1,2 = − b ± D 2 a = − 1 ± 25 2 ⋅ 1 = − 1 ± 5 2 = [ − 1 + 5 2 = 4 2 = 2 − 1 − 5 2 = − 6 2 = − 3

Корни, полученные на предыдущем шаге:

Значит, в ответ идет только один корень, x = − 3.

Задания для самостоятельного решения

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

Решение:

[ x − 19 ≠ 0 x − 3 ≠ 0 ⇒ [ x ≠ 19 x ≠ 3

Приводим обе дроби к общему знаменателю, записываем дополнительные множители к числителям:

3 \ ( x − 3 ) x − 19 − 19 \ ( x − 19 ) x − 3 = 0

3 ( x − 3 ) − 19 ( x − 19 ) ( x − 19 ) ( x − 3 ) = 0

В соответствии с алгоритмом, приравниваем числитель к нулю:

3 x − 9 − 19 x + 361 = 0

x = − 352 − 16 = − 352 16 = 22

Полученный корень не входит в ОДЗ, так что смело можем его включать в ответ.

№2. Решите уравнение x − 4 x − 6 = 2.

Решение:

Можно решать эту задачу способом, который использовался при решении задачи №8. Но сейчас мы используем еще один способ решения таких уравнений.

Воспользуемся основным свойством пропорции :

произведение крайних членов равно произведению средних (правило «креста»):

a b = c d ⇒ a ⋅ d = b ⋅ c

x − 4 x − 6 = 2 1 ⇒ ( x − 4 ) ⋅ 1 = ( x − 6 ) ⋅ 2

Полученный корень не входит в ОДЗ, так что смело можем его включать в ответ.

Источник

Рациональные уравнения (ЕГЭ 2022)

Рациональные уравнения – это уравнения, в которых и левая, и правая части – рациональные выражения.

Ну… Это было сухое математическое определение, и слово-то какое: «рациональные». А по сути, рациональные выражения – это просто целые и дробные выражения без знака корня.

А получается, что под пугающим «рациональным уравнением» скрывается всего лишь уравнение, в котором могут присутствовать сложение, вычитание, умножение, деление и возведение в степень с целым показателем, но НЕ корень из переменной.

Рациональные уравнения — коротко о главном

Определение рационального уравнения:

Рациональное уравнение – это равенство двух рациональных (без знака корня) выражений.

Дробно-рациональное уравнение – рациональное (без знака корня) уравнение, в котором левая или правая части являются дробными выражениями.

Алгоритм решения рациональных уравнений:

Система для решения дробно рациональных уравнений:

Что такое рациональные уравнения?

Давай научимся отличать рациональные уравнения от иррациональных! Зачем? Рациональные уравнения решать проще.

А зачем работать больше, если можно работать меньше?

Надеюсь, теперь ты сможешь различать, к какому виду относится уравнение. (И не поедешь из Москвы в Петербург через Магадан, решая рациональные уравнения как нерациональные).

Целые рациональные уравнения

Важно знать, что рациональные уравнения в свою очередь тоже разные бывают.

Если в дроби нет деления на переменную (то есть на \( \displaystyle x\), \( \displaystyle y\) и т.д.), тогда рациональное уравнение будет называться целым (или линейным) уравнением, вот примеры:

Умеешь такие решать? – конечно, умеешь, упрощаешь и находишь неизвестное, тема-то 5-ого или 6-ого класса.

Ну, рассмотрим первый из примеров на всякий случай и по порядочку. Все неизвестные переносим влево, все известные вправо:

Какой наименьший общий знаменатель будет?

Правильно \( \displaystyle 6\)!

Чтоб к нему привести домножаем и числитель и знаменатель первого слагаемое на \( \displaystyle 2\), а второго на \( \displaystyle 3\), этого делать не запрещено, если и числитель и знаменатель дроби умножить на одно и то же значение, то дробь от этого не изменится, т.к. ее можно будет сократить на то же число.

А \( \displaystyle 13\) не трогаем, оно нам не мешает, имеем:

А теперь делим обе части на \( \displaystyle 13\):

Поскольку уравнение целое, что мы уже определили, то и ограничений никаких нет, \( \displaystyle 6\), так \( \displaystyle 6\), ну можно для верности подставить этот ответ в исходное уравнение, получим \( \displaystyle 0=0\), значит все верно и ответ подходит (ты можешь пересчитать, а вообще должно сойтись).

Дробно-рациональные уравнения

А вот еще одно уравнение \( \displaystyle \frac<5>+\frac<4-6><(x+1)\cdot (x+3)>=3\).

Это уравнение целое? НЕТ. Тут есть деление на переменную \( \displaystyle x\), а это говорит о том, что уравнение не целое. Тогда какое же оно? Это дробно рациональное уравнение.

Дробно-рациональное уравнение – рациональное (без знака корня) уравнение, в котором левая или правая части являются дробными выражениями.

На первый взгляд особой разницы не видно, ну давай попробуем решать его как мы решали целое (линейное) уравнение.

Для начала найдем наименьший общий знаменатель, это будет \( \displaystyle (x+1)\cdot (x+3)\).

Важный момент!

В предыдущем примере, где было целое уравнение мы не стали свободный член \( \displaystyle 13\) приводить к знаменателю, т.к. умножали все на числа без переменных, но тут-то наименьший общий знаменатель \( \displaystyle (x+1)\cdot (x+3)\).

А это тебе не шутки, переменная в знаменателе!

Решая дробно-рациональное уравнение, обе его части умножаем на наименьший общий знаменатель!

Это надеюсь, ты запомнишь, но давай посмотрим что вышло:

Что-то оно огромное получилось, надо все посокращать:

\( \displaystyle 5(x+3)+(4-6)=3\cdot (x+1)\cdot (x+3)\).

Раскроем скобки и приведем подобные члены:

Ну как, это уже попроще выглядит, чем в начале было?

Выносим за скобку общий множитель: \( \displaystyle 3x\cdot (x+1)=0\)

У этого уравнения два решения, его левая сторона принимает нулевое значение при \( \displaystyle x=0\) и \( \displaystyle x=-1\).

Вроде бы все, ну ладно давайте напоследок подставим корни \( \displaystyle x=0\) и \( \displaystyle x=-1\) в исходное уравнение, чтобы проверить, нет ли ошибок. Сначала подставим \( \displaystyle 0\), получается \( \displaystyle 3=3\) –нет претензий?

Но ведь это же будет ноль!

На ноль делить нельзя, это все знают, в чем же дело.

Дело в ОДЗ — Области Допустимых Значений!

Всякий раз когда ты видишь уравнение, где есть переменные (\( \displaystyle x,y\) и т.д.) в знаменателе, прежде всего, нужно найти ОДЗ, найти какие значения может принимать икс.

Хотя удобнее в ОДЗ написать, чему икс НЕ может быть равен, ведь таких значений не так много, как правило.

Просто запомни, что на ноль делить нельзя! И перед тем как решать наше уравнение нам следовало сделать так:

Если бы мы сразу так написали, то заранее бы знали, что эти ответы стоит исключить и так, из полученных нами \( \displaystyle x=0\) и \( \displaystyle x=-1\) мы смело исключаем \( \displaystyle x=-1\), т.к. он противоречит ОДЗ.

Значит, какой ответ будет у решенного уравнения?

В ответ стоит написать только один корень, \( \displaystyle x=0\).

Стоит заметить, что ОДЗ не всегда сказывается на ответе, возможны случаи, когда корни, которые мы получили, не попадают под ограничения ОДЗ.

Но писать ОДЗ в дробно рациональных уравнениях стоит всегда – так просто спокойнее, что ты ничего не упустил и да,

ВСЕГДА по окончании решения сверяй свои корни и область допустимых значений!

Алгоритм решения рационального уравнения

Усвоил, говоришь? А ты докажи! 🙂 Вот тебе примеры на закрепление. Попробуй решить сам, а потом сверься с ответом.

Источник

Дробно-рациональные уравнения. Алгоритм решения

Пример не дробно-рациональных уравнений:

Как решаются дробно-рациональные уравнения?

Алгоритм решения дробно-рационального уравнения:

Выпишите и «решите» ОДЗ.

Умножьте каждый член уравнения на общий знаменатель и сократите полученные дроби. Знаменатели при этом пропадут.

Запишите уравнение, не раскрывая скобок.

Решите полученное уравнение.

Проверьте найденные корни с ОДЗ.

Запишите в ответ корни, которые прошли проверку в п.7.

Алгоритм не заучивайте, 3-5 решенных уравнений – и он запомнится сам.

Пример. Решите дробно-рациональное уравнение \(\frac — \frac<7>=\frac<8>\)

Сначала записываем и «решаем» ОДЗ.

По формуле сокращенного умножения : \(x^2-4=(x-2)(x+2)\). Значит, общий знаменатель дробей будет \((x-2)(x+2)\). Умножаем каждый член уравнения на \((x-2)(x+2)\).

Сокращаем то, что можно и записываем получившееся уравнение.

Приводим подобные слагаемые

Пример. Найдите корни дробно-рационального уравнения \(\frac + \frac-\frac<7-x>\) \(=0\)

Записываем и «решаем» ОДЗ.

Очевидно, общий знаменатель дробей: \((x+2)(x+5)\). Умножаем на него всё уравнение.

Приводим подобные слагаемые

Находим корни уравнения

Один из корней не подходи под ОДЗ, поэтому в ответ записываем только второй корень.

Источник

• ← кота заели блохи что делать
• чем заменить тягу верхнего блока в домашних условиях →