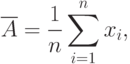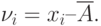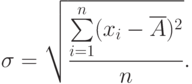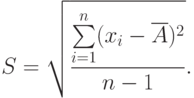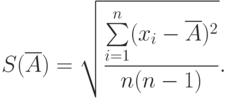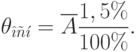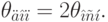что такое достоверность результата измерений
Что такое достоверность измерений?



Основная характеристика измерений – это достоверность измерений.
Достоверность измерений – это характеристика, определяющая степень доверия к полученным результатам измерений. По данной характеристике измерения делятся на достоверные и недостоверные. Достоверность измерений зависит того, известна ли вероятность отклонения результатов измерения от настоящего значения измеряемой величины. Если же достоверность измерений не определена, то результаты таких измерений, как правило, не используются. Достоверность измерений ограничена сверху погрешностью измерений.
Что такое воспроизводимость результатов измерений?
Примечание: Воспроизводимость измерений может характеризоваться средними квадратическими погрешностями сравниваемых рядов измерений.
Перечислите общие способы обнаружения и уменьшения систематических погрешностей.
Для устранения систематических погрешностей в процессе уже начатого измерения применяются различные способы
Способ введения поправок базируется на знании систематической погрешности и действующих закономерностей ее изменения. При использовании данного способа в результат измерения, полученный с систематическими погрешностями, вносят поправки, по величине равные этим погрешностям, но обратные по знаку.
Способ замещения состоит в том, что измеряемая величина заменяется мерой, помещенной в те же самые условия, в которых находился объект измерения. Способ замещения применяется при измерении следующих электрических параметров: сопротивления, емкости и индуктивности.
Способ компенсации погрешности по знаку состоит в том, что измерения выполняются два раза таким образом, чтобы погрешность, неизвестная по величине, включалась в результаты измерений с противоположным знаком.
Способ противопоставления похож на способ компенсации по знаку. Данный способ состоит в том, что измерения выполняют два раза таким образом, чтобы источник погрешности при первом измерении противоположным образом действовал на результат второго измерения.
Перечислите специальные способы обнаружения и уменьшения систематических погрешностей.
Основы общей теории измерений
2.4. Точность и достоверность результата измерения
Применение рассмотренных выше элементов общей теории измерений необходимо для обеспечения точности и достоверности результата измерения. При многократных наблюдениях получают ряд значений, обрабатывая которые находят результат измерения. Для обработки применяют инструменты математической статистики, рассматривая ряд значений как выборку из генеральной совокупности. Опираясь на теорию вероятностей, математическая статистика позволяет оценить надежность и точность выводов, делаемых на основании ограниченного статистического материала.
Требуемая точность технических измерений может также обеспечиваться повторением многократных наблюдений. В этом случае многократные наблюдения одного и того же объекта выполняются несколько раз. Чтобы сократить время, необходимое для обработки нескольких рядов многократных наблюдений, в начале процесса обработки применяют индикаторы, позволяющие определить предпочтительный ряд и в дальнейшем обрабатывать только этот ряд.
Такими индикаторами является сумма остаточных погрешностей и сумма квадратов остаточных погрешностей. Эти индикаторы являются косвенной характеристикой несмещенности и эффективности оценки, полученной при обработке результатов многократных наблюдений.
Однако симметричность не является исчерпывающей характеристикой распределения. Следующим важным в метрологии признаком является компактность распределения. По этому признаку при фиксированном числе наблюдений предпочтительный ряд может быть определен индикатором эффективности. Эффективной называется та из нескольких возможных несмещенных оценок, которая имеет наименьшую дисперсию. Условию эффективности будет удовлетворять ряд с наименьшей суммой квадратов остаточных погрешностей.
Очевидно, что в практической метрологии эффективная оценка является предпочтительной. Признак эффективности свидетельствует о том, что субъективная составляющая случайной погрешности минимальна, наблюдения выполнялись более аккуратно и будет обеспечен наименьший размер случайной погрешности.
В теоретической метрологии рассматривается также состоятельная оценка, являющаяся идеальной моделью для многократных измерений, к которой желательно стремиться, но получить ее практически невозможно. При состоятельной оценке истинное и действительное значение совпадают, погрешность равна нулю. Это достигается бесконечным увеличением числа наблюдений. Состоятельной называется оценка, в которой при числе наблюдений, стремящемся к бесконечности, дисперсия стремится к нулю.
Задавая большую степень неопределенности контролируемым посредством измерений событиям, мы получаем большую уверенность в том, что они произойдут.
2.5. Прямые равноточные измерения с многократными наблюдениями
Метод прямых равноточных измерений с многократными наблюдениями является основополагающим, используется в технических измерениях для повышения достоверности результата, является основой для многих методов метрологических измерений, для методов косвенных измерений.
Равноточность измерений истолковывается в широком смысле, как одинаковая распределенность (в узком смысле равноточность измерений понимается как одинаковость меры точности всех результатов измерений). Наличие грубых ошибок (промахов) означает нарушение равноточности как в широком, так и в узком смысле.
Результат измерения находят как среднее арифметическое результатов наблюдений:
где 
Для оценки среднего квадратического отклонения результата измерения находим случайные отклонения результатов отдельных наблюдений, принимаем их за остаточные погрешности,
Для минимизации случайной и систематической составляющих погрешности, при наличии нескольких групп наблюдений (реализаций), используют два свойства остаточных погрешностей: сумма остаточных погрешностей равна нулю,
и сумма квадратов остаточных погрешностей минимальна,
Для дальнейших вычислений рекомендуется выбрать реализацию, удовлетворяющую этим условиям.
Степень рассеяния результатов наблюдений вокруг среднего арифметического значения характеризуется средним квадратическим отклонением, (СКО):
Оценка СКО учитывает ограниченность объем а выборки: при малом объем е выборки оценка СКО будет заметно больше, чем СКО, а при большом объем е выборки оценка СКО не будет заметно отличаться от СКО.
Полученное значение СКО результатов наблюдения не так универсально, как среднее арифметическое исправленных результатов наблюдений и не может быть непосредственно принято за значение случайной погрешности результата измерения. Для этого, прежде всего, необходимо восстановить размерность физической величины, ликвидировав нелинейность преобразования физической величины, разделив СКО результатов наблюдения на корень из 
Предположим, что наблюдения были получены в результате измерения цифровым вольтметром, имеющим класс точности, обозначенный цифрой 1,5 в кружочке, причем условия измерения выходили за нормальные пределы.
Основная инструментальная погрешность :
Дополнительная инструментальная погрешность :