что такое длинная арифметика
Реализация длииииииинной арифметики на C++
Структура класса
Первое, что нужно решить — это то, как хранить наше число. Я храню его в виде массива цифр, в обратном порядке (это позволяет проще реализовывать все операции), сразу по 9 цифр в одном элементе массива (что позволяет сэкономить память):
В моей реализации будет сразу два представления нуля — в виде пустого вектора и в виде вектора с одним-единственным нулём.
Создание числа
Первое, что нужно научиться делать — это создавать число. Вот так оно преобразуется из строки, содержащей цифры:
Код процедуры удаления ведущих нулей прост до безобразия:
Также нам нужно уметь преобразовывать обычные числа в длинные:
Код преобразования из остальных типов еще проще, я не стал приводить его здесь.
Вывод числа
Теперь нам нужно научиться печатать наше число в поток и преобразовывать его в строку:
Сравнение чисел
Теперь нам нужно научиться сравнивать два числа друг с другом. Теория говорит, что для этого достаточно всего двух операций, остальные могут быть выведены на их основе. Итак, сначала научимся сравнивать два числа на равенство:
Теперь проверим, меньше ли одно число другого:
Здесь мы используем унарное отрицание, чтобы сменить знак числа. Также я для симметрии ввел унарный плюс:
Знания о том, почему нужно возвращать const big_integer, а не просто big_integer, а также о правилах выбора между дружественной функцией-оператором и оператором-членом класса, я подчерпнул из этой статьи.
Дальше все совсем просто:
Арифметические операции
Сложение
Я не стал мудрить с операциями и реализовал обычное школьное сложение в столбик. Поскольку нам в любом случае нужно будет создать новое число как результат операции, я сразу копирую в стек левый операнд по значению и прибавляю числа непосредственно к нему:
Здесь я избежал «дорогой» операции деления в случае, когда получившаяся «цифра» больше основания, по которому я работаю, путем простого сравнения.
Вычитание
В принципе, вычитание аналогично сложению. Нужно лишь рассмотреть случай, когда уменьшаемое меньше вычитаемого:
Инкремент и декремент
Перед реализацией этих двух операций нам нужно реализовать сложение и вычитание с присвоением:
Тогда префиксные версии операций реализуются в одну строчку, а постфиксные — лишь немногим сложнее:
Умножение
Я не стал писать быстрое умножение Карацубы, а снова использовал «школьную» арифметику:
Деление
Поскольку я не нашел в Интернете быстрых способов деления, воспользуемся школьным делением уголком. Начнем делить со старших разрядов. Нам нужно уменьшить текущее значение делимого на максимально возможное число делимым. Это максимальное значение будем искать двоичным поиском. Но сначала нам нужно определить функцию «сдвига» числа вправо, которая позволит нам перебирать разряды последовательно:
Теперь опишем само деление:
Взятие остатка
Возведение в степень
Я использовал алгоритм быстрого возведения в степень. Он требует проверки числа на нечетность. Поскольку вычислять остаток от деления на 2, мягко говоря, было бы затратно, введем такие операции:
Теперь напишем само возведение:
Арифметика чисел в b-ичной системе счисления (Длинная арифметика)
| Определение: |
| Длинная арифметика (англ. arbitrary-precision arithmetic, или bignum arithmetic) — это набор программных средств (структуры данных и алгоритмы), которые позволяют работать с числами гораздо больших величин, чем это позволяют стандартные типы данных. |
| Определение: |
| Классическая длинная арифметика — длинная арифметика, основная идея которой заключается в том, что число хранится в виде массива его цифр. Цифры могут использоваться из той или иной системы счисления, обычно применяются десятичная система счисления и её степени (десять тысяч, миллиард), двоичная система счисления либо любая другая. |
Содержание
Представление в памяти [ править ]
Цифры будут храниться в массиве в следующем порядке: сначала идут наименее значимые цифры (т.е., например, единицы, десятки, сотни, и т.д.).
Кроме того, все операции реализуются таким образом, что после выполнения любой из них лидирующие нули (т.е. лишние нули в начале числа) отсутствуют (разумеется, в предположении, что перед каждой операцией лидирующие нули также отсутствуют). Следует отметить, что в представленной реализации для числа ноль корректно поддерживаются сразу два представления: пустой вектор цифр, и вектор цифр, содержащий единственный элемент — ноль.
Операции над числами [ править ]
Операции над числами производятся с помощью «школьных» алгоритмов сложения, вычитания, умножения, деления столбиком. После совершения операций следует не забывать удалять лидирующие нули, чтобы поддерживать предикат о том, что таковые отсутствуют. К ним также применимы алгоритмы быстрого умножения: Быстрое преобразование Фурье и Алгоритм Карацубы.
Приведённые ниже алгоритмы корректны в силу того, что они являются реализацией «школьных» алгоритмов действий в столбик:
[math]A = abc = 100 \cdot a + 10 \cdot b + c [/math]
[math]B = de = 10 \cdot d + e [/math]
Тогда сумма [math]A + B = abc + de = (100 \cdot a + 10 \cdot b + c) + (10 \cdot d + e) = 100 \cdot a + 10 \cdot (b + d) + (c + e) [/math]
Произведение [math]A \cdot B = abc \cdot de = (100 \cdot a + 10 \cdot b + c) \cdot (10 \cdot d + e) = 100 \cdot a \cdot 10 \cdot d + 10 \cdot b \cdot 10 \cdot d + c \cdot 10 \cdot d + 100 \cdot a \cdot e + 10 \cdot b \cdot e + c \cdot e = 1000 \cdot a \cdot d + 100 \cdot (a \cdot e + b \cdot d) + 10 \cdot (b \cdot e + c \cdot d) + c \cdot e[/math]
Сложение [ править ]
Прибавляет к числу [math]a[/math] число [math]b[/math] и сохраняет результат в [math]a[/math] :
Алгоритм не требует дополнительной памяти.
Вычитание [ править ]
Отнимает от числа [math]a[/math] число [math]b\,(a \geqslant b)[/math] и сохраняет результат в [math] a[/math] :
Алгоритм не требует дополнительной памяти.
Умножение длинного на короткое [ править ]
Умножает длинное [math]a[/math] на короткое [math]b\, (b \lt base)[/math] и сохраняет результат в [math]a[/math] :
Алгоритм требует [math]O(n)[/math] памяти, где [math]n[/math] — длина длинного числа.
Умножение двух длинных чисел [ править ]
Умножает [math]a[/math] на [math]b[/math] и результат сохраняет в [math]c[/math] :
Деление длинного на короткое [ править ]
Длинная арифметика от Microsoft
Введение
А что делать, если надо представить число, такое как, например, 29! = 8841761993739701954543616000000? Такое число не поместится ни в 64-х разрядный, ни тем более 32-х разрядный тип данных. Именно для работы с такими большими числами существует длинная арифметика.
Длинная арифметика — в вычислительной технике операции (сложение, умножение, вычитание, деление, возведение в степень и т.д.) над числами, разрядность которых превышает длину машинного слова данной вычислительной машины. Эти операции реализуются не аппаратно, а программно, используя базовые аппаратные средства работы с числами меньших порядков.
Длинную арифметику также можно считать одним из разделов олимпиадного программирования, поскольку очень часто при решении задач, разрядности стандартных типов не хватает для представления конечного результата. При выборе языка программирования для олимпиадных нужд не маловажным является встроенный в него набор средств (готовых библиотек, реализованных классов). Многие языки (Java, Ruby, Python) имеют встроенную поддержку длинной арифметики, что в разы может сократить время написания программы.
В данной статье я бы хотел рассмотреть подробности реализации длинной арифметики от Microsoft.
Общие понятия
Идея представления длинных чисел в памяти компьютера достаточно проста. Рассмотрим число 123456789 в десятеричной системе счисления. Очевидно, его можно представить следующим образом:
12345678910 = 1*10 8 + 2*10 7 + 3*10 6 + 4*10 5 + 5*10 4 + 6*10 3 + 7*10 2 + 8*10 1 + 9*10 0
В общем случае, любое число можно представить в виде:
A = an-1β n-1 + an-2β n-2 +…+a1β + a0
где β – основание системы счисления, в которой мы представляем число, а коэффициенты ai удовлетворяют двойному неравенству 0 ≤ ai 2 + … + anx n удобно представлять в виде массива, элементы которого представляют коэффициенты ai, а индекс i — определяет соответствующую степень x. Длинное число хранится аналогично, осталось определиться с выбором основания β.
Например, то же самое число 123456789 можно представить в десятитысячной (β = 10 4 ) системе счисления следующим образом:
12345678910 = 1*(10 4 ) 2 + 2345*(10 4 ) 1 + 6789*(10 4 ) 0
Представляя число 123456789 в десятитысячной системе счисления, мы получаем сразу два преимущества: во-первых, сокращаем количество потребляемой памяти, так как вместо массива из 9 чисел нам достаточно хранить массив из 3 чисел (1, 2345 и 6789), во-вторых, значительно уменьшаем время выполнения стандартных операций над длинными числами, поскольку за раз обрабатываем 4 разряда числа. В общем, компьютер одинаково быстро складывает одноразрядные и 32-разрядные числа, поэтому этим следует воспользоваться.
Основание системы счисления β обычно зависит от максимального размера базового типа данных на компьютере, и выбирается, исходя из следующих соображений:
BigInteger от Microsoft
Если посмотреть на структуру BigInteger через декомпилятор Reflector или dotPeek, то увидим следующие поля:
Можно предположить, что в переменной _sign хранится знак числа, а массив _bits содержит коэффициенты ai. Учитывая, что массив _bits имеет тип uint[], можно так же предположить, что в качестве основания β взята степень двойки 2 32 (поскольку uint — 32 разрядное беззнаковое число).
Итак, попробуем подтвердить или опровергнуть наши предположения.
Конструктор, принимающий int, в качестве аргумента выглядит так:
Конструктор, принимающий uint в качестве аргумента, выглядит следующим образом:
В зависимости от того помещается ли число в int диапазон, оно записывается либо в переменную _sign, либо в массив _bits.
Следующий конструктор, принимающий 64-х разрядное число со знаком (long) поможет ответить на вопрос о выборе основания системы счисления:
Если число не помещается в int диапазон, то, как мы видим переменная _sign содержит знак числа (-1 – для отрицательного и 1 – для положительного), а массив _bits содержит те самые коэффициенты ai и заполняется следующим образом:
В данном случае 64-х разрядное число num разбивается на два 32-х разрядных: (uint)num и (uint)(num >> 32). Первое число представляет собой последние 32 бита числа num, в то время как второе первые 32 бита (смещение вправо на n бит равносильно целочисленному делению на 2 n ).

Фактически (uint)long.MaxValue = 4294967295, (uint)(long.MaxValue >> 32) = 2147483647.
_sign = 1
_bits = <4294967295, 2147483647>// вспоминаем, что число храниться задом наперёд
То есть число раскладывается по степеням 2 32 следующим образом:
1234567891011121314151617181920 = 15*(2 32 ) 3 + 2501550035*(2 32 ) 2 + 3243814879*(2 32 ) 1 + 4035623136*(2 32 ) 0
Значит, BigInteger будет представлен парой:
Число, помещающееся в int диапазон, скажем, 17 будет храниться следующим образом:
_sign = 17
_bits = null
Исследовав конструкторы структуры BigInteger можно заключить:
Для языков, не поддерживающих пользовательские операторы, структура BigInteger также предоставляет эквивалентные методы для выполнения математических операций. Это относится к методам Add, Divide, Multiply, Negate, Subtract и некоторым другим. Точно так же Microsoft поступило в реализации структуры Decimal.
Многие члены структуры BigInteger напрямую соответствуют членам других целых типов. Кроме того, BigInteger добавляет такие элементы как:
Пару слов о BigInteger в Mono и Java
Следует отметить, что Mono так же обладает поддержкой длинной арифметики. Реализация структуры BigInteger в Mono практически ничем не отличается от реализации Microsoft, кроме как, того что в ней нет оптимизации для чисел представимых типом int.
То есть число 17 в Mono будет представлено парой:
_sign = 1 // знак числа
_bits =
Аналогичная реализация BigInteger представлена в Java:
В Java, так же как и в Mono нет оптимизации для чисел, представимых типом int.
Производительность BigInteger
Работая с длинным числом BigInteger, необходимо помнить о возможных проблемах связанных с производительностью. Например, казалось бы, безобидный оператор ++ может оказать существенное влияние на производительность:
Хотя, кажется, что в этом примере происходит изменение значения существующего объекта, это не так. Объекты BigInteger неизменяемы, то есть внутренне, общеязыковая среда выполнения фактически создает новый объект BigInteger и присваивает ему значение на единицу больше предыдущего.
В данном примере, можно поступить следующим образом: выполнить промежуточные операции, используя обычные числовые типы, а затем использовать BigInteger:
Вместо заключения
За замечание спасибо пользователям: gouranga
Длинная арифметика
Длинная арифметика — это набор программных средств (структуры данных и алгоритмы), которые позволяют работать с числами гораздо больших величин, чем это позволяют стандартные типы данных.
Виды целочисленной длинной арифметики
Вообще говоря, даже только в олимпиадных задачах набор средств достаточно велик, поэтому произведём классификацию различных видов длинной арифметики.
Классическая длинная арифметика
Основная идея заключается в том, что число хранится в виде массива его цифр.
Цифры могут использоваться из той или иной системы счисления, обычно применяются десятичная система счисления и её степени (десять тысяч, миллиард), либо двоичная система счисления.
Операции над числами в этом виде длинной арифметики производятся с помощью «школьных» алгоритмов сложения, вычитания, умножения, деления столбиком. Впрочем, к ним также применимы алгоритмы быстрого умножения: Быстрое преобразование Фурье и Алгоритм Карацубы.
Здесь описана работа только с неотрицательными длинными числами. Для поддержки отрицательных чисел необходимо ввести и поддерживать дополнительный флаг «отрицательности» числа, либо же работать в дополняющих кодах.
Структура данных
Хранить длинные числа будем в виде вектора чисел 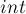
Для повышения эффективности будем работать в системе по основанию миллиард, т.е. каждый элемент вектора 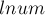
Цифры будут храниться в векторе в таком порядке, что сначала идут наименее значимые цифры (т.е. единицы, десятки, сотни, и т.д.).
Кроме того, все операции будут реализованы таким образом, что после выполнения любой из них лидирующие нули (т.е. лишние нули в начале числа) отсутствуют (разумеется, в предположении, что перед каждой операцией лидирующие нули также отсутствуют). Следует отметить, что в представленной реализации для числа ноль корректно поддерживаются сразу два представления: пустой вектор цифр, и вектор цифр, содержащий единственный элемент — ноль.
Вывод
Самое простое — это вывод длинного числа.
Сначала мы просто выводим самый последний элемент вектора (или 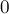
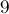
(здесь небольшой тонкий момент: нужно не забыть записать приведение типа 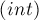
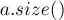
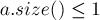
Чтение
Считываем строку в 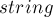
Если использовать вместо 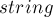
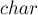
Если во входном числе уже могут быть лидирующие нули, то их после чтения можно удалить таким образом:
Сложение
Прибавляет к числу 


Вычитание
Отнимает от числа 

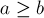

Здесь мы после выполнения вычитания удаляем лидирующие нули, чтобы поддерживать предикат о том, что таковые отсутствуют.
Умножение длинного на короткое
Умножает длинное 

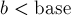

Здесь мы после выполнения деления удаляем лидирующие нули, чтобы поддерживать предикат о том, что таковые отсутствуют.
(Примечание: способ дополнительной оптимизации. Если скорость работы чрезвычайно важна, то можно попробовать заменить два деления одним: посчитать только целую часть от деления (в коде это переменная 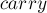
Умножение двух длинных чисел
Умножает 


Деление длинного на короткое
Делит длинное 

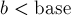

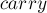
Длинная арифметика в факторизованном виде
Здесь идея заключается в том, чтобы хранить не само число, а его факторизацию, т.е. степени каждого входящего в него простого.
Этот метод также весьма прост для реализации, и в нём очень легко производить операции умножения и деления, однако невозможно произвести сложение или вычитание. С другой стороны, этот метод значительно экономит память в сравнении с «классическим» подходом, и позволяет производить умножение и деление значительно (асимптотически) быстрее.
Этот метод часто применяется, когда необходимо производить деление по непростому модулю: тогда достаточно хранить число в виде степеней по простым делителям этого модуля, и ещё одного числа — остатка по этому же модулю.
Длинная арифметика по системе простых модулей (Китайская теорема или схема Гарнера)
Суть в том, что выбирается некоторая система модулей (обычно небольших, помещающихся в стандартные типы данных), и число хранится в виде вектора из остатков от его деления на каждый из этих модулей.
Как утверждает Китайская теорема об остатках, этого достаточно, чтобы однозначно хранить любое число в диапазоне от 0 до произведения этих модулей минус один. При этом имеется Алгоритм Гарнера, который позволяет произвести это восстановление из модульного вида в обычную, «классическую», форму числа.
Таким образом, этот метод позволяет экономить память по сравнению с «классической» длинной арифметикой (хотя в некоторых случаях не столь радикально, как метод факторизации). Крому того, в модульном виде можно очень быстро производить сложения, вычитания и умножения, — все за асимптотически однаковое время, пропорциональное количеству модулей системы.
Однако всё это даётся ценой весьма трудоёмкого перевода числа из этого модульного вида в обычный вид, для чего, помимо немалых временных затрат, потребуется также реализация «классической» длинной арифметики с умножением.
Помимо этого, производить деление чисел в таком представлении по системе простых модулей не представляется возможным.
Виды дробной длинной арифметики
Операции над дробными числами встречаются в олимпиадных задачах гораздо реже, и работать с огромными дробными числами значительно сложнее, поэтому в олимпиадах встречается только специфическое подмножество дробной длинной арифметики.
Длинная арифметика в несократимых дробях
Число представляется в виде несократимой дроби 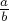


Обычно при этом для хранения числителя и знаменателя приходится также использовать длинную арифметику, но, впрочем, самый простой её вид — «классическая» длинная арифметика, хотя иногда оказывается достаточно встроенного 64-битного числового типа.
Выделение позиции плавающей точки в отдельный тип
Иногда в задаче требуется производить расчёты с очень большими либо очень маленькими числами, но при этом не допускать их переполнения. Встроенный 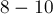
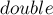
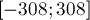
Приём, собственно, очень простой — вводится ещё одна целочисленная переменная, отвечающая за экспоненту, а после выполнения каждой операции дробное число «нормализуется», т.е. возвращается в отрезок 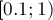
При перемножении или делении двух таких чисел надо соответственно сложить либо вычесть их экспоненты. При сложении или вычитании перед выполнением этой операции числа следует привести к одной экспоненте, для чего одно из них домножается на 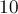
Наконец, понятно, что не обязательно выбирать