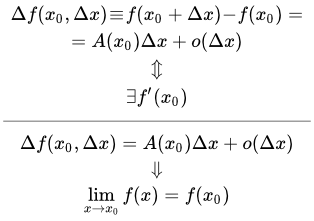что такое дифференцированная функция
Что такое дифференцированная функция
При дифференцировании различают функции по способу их задания: явные, неявные и параметрические.
Производной функции y = f ( x ) по переменной x в некоторой точке называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, то есть
Производная характеризует скорость изменения функции в достаточно малой окрестности заданной точки.
Приведем таблицу производных основных элементарных функций (без доказательства), которые рассматриваются нами как функции простые и явно заданные.
Следствие. В точках разрыва функция производной не имеет
Существуют такие точки, в которых функция непрерывна, но не дифференцируема. Так, функция y =| x | в точке x =0 непрерывна, но производной не имеет, так как в этой точке к графику функции можно провести бесконечное множество касательных (рис. 3.6). Такие точки называются угловыми или точками излома функции. Данный случай показывает, что обратное утверждение к теореме 3.9 неверно.
Среди явных функций особое место занимают обратные функции, производная которых находится с помощью следующей теоремы.
Теорема 3.10. Если строго монотонная функция y = f ( x ) дифференцируема на некотором интервале Х, причем ее производная не обращается в нуль на Х, то обратная к ней функция x = φ ( y ) также дифференцируема на этом интервале, при этом:
По определению производной можно записать:
Среди явных функций выделяют класс сложных функций.
Теорема 3.11. Чтобы продифференцировать сложную функцию необходимо сначала продифференцировать внешнюю функцию по внутренней, считая внутреннюю функцию независимой переменной, затем продифференцировать внутреннюю функцию по независимому переменному и результаты дифференцирования перемножить, то есть
Решение. Согласно формуле (3.31) и с учетом табли 
где t – параметр. Производную такой функции несложно получить:
Пример 3.9. Найти производную функции 
Решение. Согласно формуле (3.32) и с учетом табличных формул (3.18), (3.19) имеем:
Помимо таблицы производных имеют место правила дифференцирования.
Теорема 3.12. Производная суммы двух дифференцируемых функций равна сумме производных этих функций:
Данная теорема может быть обобщена для произвольного конечного числа функций-слагаемых.
Решение. Согласно формулам (3.33) и (3.31) и с учетом табличных формул (3.17), (3.20), (3.23) имеем:
Теорема 3.13. Производная произведения двух дифференцируемых функций равна произведению производной первой функции-сомножителя на вторую функцию плюс произведение первой функции на производную второй функции–сомножителя, то есть
Решение. Согласно формуле (3.34) и с учетом табличных формул (3.22), (3.24) имеем:
Теорема 3.14. Производная частного двух функций равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, то есть
Решение. Согласно формуле (3.35) и с учетом табличных формул (3.17), (3.29) имеем:
Решение. Согласно формуле (3.31) дифференцирования сложной функции и (3.34) производной произведения, с учетом табличных формул (3.17) и (3.18) имеем:
Дифференциалом функции y = f ( x ) в точке x называется главная часть приращения этой функции, равная произведению производной функции на приращение аргумента:
Формула (3.39) применяется для вычисления приближенных значений функций.
Дифференцируемая функция
Из Википедии — свободной энциклопедии
Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция — это функция, дифференцируемая в каждой точке данного множества. Дифференцируемость является одним из фундаментальных понятий в математике и имеет значительное число приложений как в самой математике, так и в других естественных науках.
Приращение дифференцируемой в данной точке функции можно представить как линейную функцию приращения аргумента с точностью до величин более высокого порядка малости. Это означает, что для достаточно малых окрестностей данной точки функцию можно заменить линейной (скорость изменения функции можно считать неизменной). Линейная часть приращения функции называется её дифференциалом (в данной точке).
Необходимым, но не достаточным условием дифференцируемости является непрерывность функции. В случае функции от одной вещественной переменной дифференцируемость равносильна существованию производной. В случае функции нескольких вещественных переменных необходимым (но не достаточным) условием дифференцируемости является существование частных производных по всем переменным. Для дифференцируемости функции нескольких переменных в точке достаточно, чтобы частные производные существовали в некоторой окрестности рассматриваемой точки и были непрерывны в данной точке. [1]
В случае функции комплексной переменной дифференцируемость в точке часто называется моногенностью и существенно отличается от понятия дифференцируемости в вещественном случае. Ключевую роль в этом играет так называемое условие Коши — Римана. Функция, моногенная в окрестности точки, называется голоморфной в этой точке. [2] [3]
В функциональном анализе существует обобщение понятия дифференцирования на случай отображений бесконечномерных пространств — производные Гато и Фреше.
Обобщением понятия дифференцируемой функции являются понятия субдифференцируемых, супердифференцируемых и квазидифференцируемых функций.
Дифференцируемые функции в точке – определение и свойства
Определение дифференцируемой функции
Как мы увидим ниже, определение дифференцируемой функции одной переменной эквивалентно существованию ее производной. Тогда возникает вопрос – почему нельзя сразу дать определение, что дифференцируемая функция – это функция, имеющая производную?
Ответ на этот вопрос раскрывается при рассмотрении функций нескольких переменных. Дело в том, что производные вычисляются только от функций, зависящих от одной переменной. Для функций двух и более переменных, вначале выбирают направление приближения к заданной точке (например, ось x или ось y ), а затем по этому направлению вычисляют производную. Поэтому в любой точке имеется бесконечное множество производных по различным направлением. Из-за этого производные не фигурируют в определении дифференцируемой функции.
Свойства дифференцируемой функции
Таким образом, в случае функции от одной переменной, дифференцируемость функции в точке эквивалентно существованию производной в этой точке. Забегая вперед укажем, что в случае функций многих переменных, для того чтобы функция была дифференцируемой в точке, необходимо, чтобы она имела в этой точке частные производные, и достаточно, чтобы она имела в этой точке непрерывные частные производные.
Доказательства теорем
Связь дифференцируемости функции с существованием производной
В нашем случае это означает, что
.
Отсюда
.
Связь дифференцируемости функции с ее непрерывностью
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Дифференцируемая функция
Приращение дифференцируемой в данной точке функции можно представить как линейную функцию приращения аргумента с точностью до величин более высокого порядка малости. Это означает, что для достаточно малых окрестностей данной точки функцию можно заменить линейной (скорость изменения функции можно считать неизменной). Линейная часть приращения функции называется её дифференциалом (в данной точке).
Необходимым, но не достаточным условием дифференцируемости является непрерывность функции. В случае функции от одной вещественной переменной дифференцируемость равносильна существованию производной. В случае функции нескольких вещественных переменных необходимым (но не достаточным) условием дифференцируемости является существование частных производных по всем переменным. Для дифференцируемости функции нескольких переменных в точке достаточно, чтобы частные производные существовали в некоторой окрестности рассматриваемой точки и были непрерывны в данной точке.В случае функции комплексной переменной дифференцируемость в точке часто называется моногенностью и существенно отличается от понятия дифференцируемости в вещественном случае. Ключевую роль в этом играет так называемое условие Коши — Римана. Функция, моногенная в окрестности точки, называется голоморфной в этой точке.В функциональном анализе существует обобщение понятия дифференцирования на случай отображений бесконечномерных пространств — производные Гато и Фреше.
Обобщением понятия дифференцируемой функции являются понятия субдифференцируемых, супердифференцируемых и квазидифференцируемых функций.
Дифференцируемость
Дифференци́руемая фу́нкция в математическом анализе — это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат.
Содержание
Определения
где 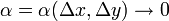
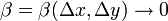
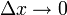
Свойства
Касательная прямая
Примеры
См. также
Ссылки
Полезное
Смотреть что такое «Дифференцируемость» в других словарях:
Дифференцируемость функции в точке — Дифференцируемая функция в математическом анализе это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так… … Википедия
Непрерывная дифференцируемость — Дифференцируемая функция в математическом анализе это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так… … Википедия
АППРОКСИМАТИВНАЯ ДИФФЕРЕНЦИРУЕМОСТЬ — обобщение понятия дифференцируемости с заменой обычного предела аппроксимативным пределом. Действительная функция действительного переменного наз. аппроксимативно дифференцируемой в точке х 0, если существует такое число А, что При этом величина… … Математическая энциклопедия
Аналитические функции — функции, которые могут быть представлены степенными рядами (См. Степенной ряд). Исключительная важность класса А. ф. определяется следующим. Во первых, этот класс достаточно широк; он охватывает большинство функций, встречающихся в… … Большая советская энциклопедия
Дифференцируемая функция — Дифференцируемая (в точке) функция это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция это функция, дифференцируемая в каждой точке данного множества. Дифференцируемость является… … Википедия
Лобачевский, Николай Иванович — родился 22 октября 1793 г. в Нижегородской губернии (по одному источнику в Нижнем Новгороде, по другому в Макарьевском уезде). Отец его Иван Максимович, выходец из Западного края, по вероисповеданию католик, потом перешедший в православную веру,… … Большая биографическая энциклопедия
АНАЛИТИЧЕСКАЯ ФУНКЦИЯ — функция, к рая может быть представлена степенным рядом. Исключит, важность класса А. ф. определяется следующим. Во первых, этот класс достаточно ш и р о к: он охватывает большинство функций, встречающихся в основных вопросах математики и ее… … Математическая энциклопедия
Производная функции — У этого термина существуют и другие значения, см. Производная. Иллюстрация понятия производной Производная&# … Википедия
Голоморфная функция — осуществляет конформное отображение, преобразуя ортогональную сетку в ортогональную (там где комплексная производная не обращается в нуль). Голоморфная функция, также называемая регулярно … Википедия